Kinematic and Dynamic Modeling Based on Trajectory Tracking Control of Mobile Robot with Mecanum Wheels
Corresponding email: hassan.m.alwan@uotechnology.edu.iq
Published at : 18 Sep 2024
Volume : IJtech
Vol 15, No 5 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i5.6908
Alwan, H.M., Nikolaevic, V.A., Hasan, S.F., Vladmerovna, K.O., 2024. Kinematic and Dynamic Modeling Based on Trajectory Tracking Control of Mobile Robot with Mecanum Wheels. International Journal of Technology. Volume 15(5), pp. 1473-1486
| Hassan M. Alwan | Mechanical Engineering Department, University of Technology, Alsinaa street, 10066, Baghdad, Iraq |
| Volkov A. Nikolaevic | High School of Automation and Robotics, Peter the Great St. Petersburg Polytechnic University, 29, Polytekhnicheskaya street, St. Petersburg, 195251, Russia |
| Sameh F. Hasan | Mechanical Engineering Department, University of Technology, Alsinaa street, 10066, Baghdad, Iraq |
| Kochneva O. Vladmerovna | High School of Automation and Robotics, Peter the Great St. Petersburg Polytechnic University, 29, Polytekhnicheskaya street, St. Petersburg, 195251, Russia |
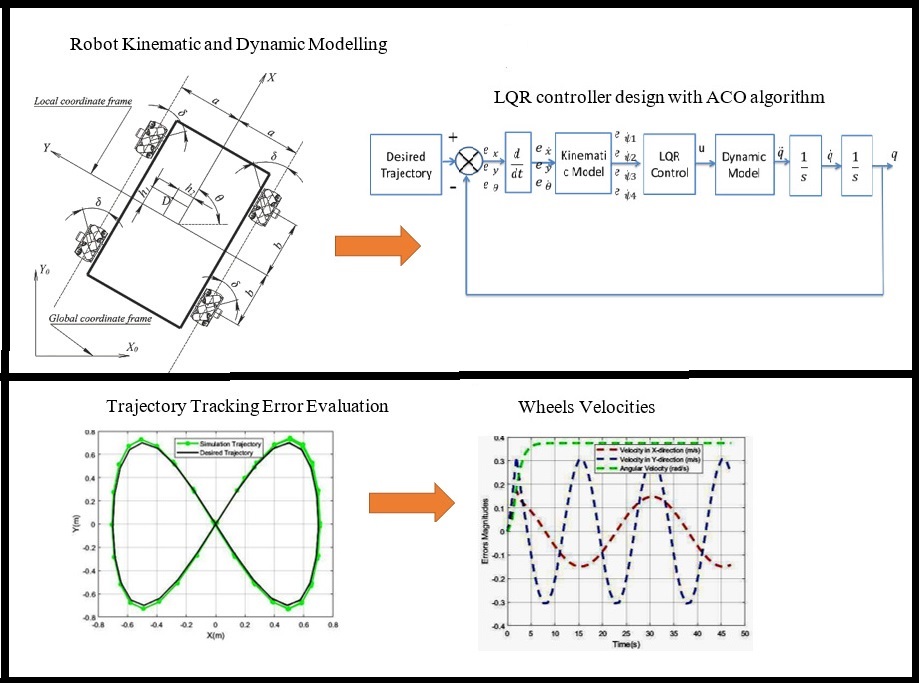
The
trajectory tracking is important to make the WMR move autonomously from the
starting point to the destination along a predefined time. Implementing of trajectory tracking control
is a fundamental part to accomplish its application tasks. In this article a
new method by using a hybrid controller has been presented to solve the problem
of the trajectory tracking of four mecanum wheeled mobile robot. Proposed
controller is depending on modeling of robot kinematic and dynamic equations.
The novelty in this work is that, an optimal control system self-tuning
parameters based on an optimization algorithm for these models of the mobile
robot is utilized. The optimal control type that is used in this work is the
Linear Quadratic Regulator (LQR) controller. LQR is used to control the
actuator torque that is required in each wheel to achieve the robot task. The parameters
of the LQR controller are tuned by using Ant Colony Optimization (ACO). For
results simulation, MATLAB/ Simulink is used for circular and infinity shape
trajectories. Results show that when the robot follows a circular trajectory, the
values of position trajectory error values are reduced to small value (ex=3.218
*10-5m) and (ey= 2.224*10-5m) in xo
and yo directions, respectively and remained almost at these values
until the end of the simulation time. The maximum orientation error is (=
0.103rad), and convergent to zero after two seconds of the mobile robot
movement. Also when the robot follows an infinity shape trajectory, the
position trajectory error values are (ey) and (
) are
reduced to small value -4.078 *10-4m and 3.174*10-4rad
respectively, while, (ex) is reduced to 5.263*10-4 m
after about 15 seconds.
Ant colony optimization; Linear quadratic regulator controller; Robot kinematics: Trajectory tracking; Wheeled mobile robot
The researches about the control of trajectory
tracking of the mobile robot (WMR) are increased dramatically. In their review paper (Abed,
Lutfy, and Al-Doori, 2021) presents various trajectory planning strategies for mobile
robots using different optimization methods proposed in last year. In
their study (Song, Tang, and Li, 2024) addressed the issue of guiding a mobile robot
through a dynamic environment by combining the enhanced ant colony optimization
ACO with the dynamic window approach DWA algorithm. (Amouri, Cherfia, and Merabti,
2021) proposed
a new method to develop kinematic and dynamic models to improve the trajectory tracking accuracy. A new dynamic window algorithm DWA is proposed
by Wang, Ma, and Zhu (2022) to set the initial direction angle and
then improve its evaluation function during implementation of the trajectory
tracking to increase the efficiency and flexibility of the algorithm. A non-singular
terminal sliding mode
control (NTSMC) was used by Sun et al. (2020) for the mobile robot trajectory
tracking. Mathematical models of the mobile robot firstly, have been obtained with taking into account the uncertainty effect. An optimal robust control strategy is designed
by (Chai et al., 2024) based on the modified backstepping method to
achieve stable, accurate and real-time trajectory tracking for the wheeled
mobile robot in the presence of unavoidable disturbances. PID and LQR controllers have been
proposed by Amudhan
et al. (2019) to use in path controlling of a four wheeled
omnidirectional robot. Circular and rectangular shapes trajectories
have been followed in the performance examination of proposed controllers.
Yuan et al., (2019) have bee applied theoretically
and experimentally the extended state observer (ESO) relaying on the sliding
mode control (SMC) for the trajectory tracking of FMWMR. ESO-SMC based on both
kinematic and dynamic models of the WMR was applied with taking into account
the effect of the uncertainty and the disturbance. Morales et al. (2018) presented
the performance analysis of FMWMR experimentally by using linear quadratic
regulator (LQR) controller. Control of trajectory tracking of the omnidirectional WMR was solved by
using the model predictive control (MPC) based on only the mobile robot
kinematic model (Wang et
al., 2018). A modified active disturbance
rejection control (ADRC) built by (Azar et al., 2023) which includes a nonlinear state error feedback
controller and nonlinear tracking differentiator (TD) for the estimation error
correction during the trajectory tracking. In work done by Malayjerdi,
Kalani, and Malayjerdi, (2018), hybrid controller consisting of self – tuning fuzzy
PID controller based on the kinematic model of FMWMR was
utilized. In their
work, (Keek, Loh, and Chong, 2018) fractional order
proportional-integral (FOPI) controller utilized experimentally for the
trajectory tracking of the FMWMR was implemented. (Khadanga et al. 2018) and Gao et al. (2017) studied the wheeled mobile robot trajectory tracking controller design. For the problem of mobile robot’s path planning
under the known environment, a path planning method of mixed artificial
potential field (APF) and ant colony optimization (ACO) based on grid map is
proposed by (Chen and Liu, 2019) to explore a new and better path to receive
stronger stability and environmental adaptability. The
kinematics and dynamics models and proposed Backstepping controller algorithm
have been derived for the trajectory tracking of the robot. Both
mathematical models for WMR were derived based on the wheels velocities and
robot mass centre point velocities. Hussein (2023) presented a new
hybrid controller based on both kinematic and dynamic models of a non-holonomic
wheeled mobile robot. The gains parameters of the hybrid controller were tuned
by applying a modified version of a grey wolf optimization. Cui et al. (2012) proposed and simulated results to show the
effectiveness of the backstepping-based controller with proven global stability
by selecting a Lyapunov
function and introducing a virtual control input for the built dynamical model.
In their paper (El-Shorbagy
and Hassanien, 2018) a comprehensive
review of PSO as a well-known population-based optimization technique used in
the field of WMR. They start by a brief
introduction to the behaviour of the PSO, and then introduced the other
representation, convergence properties and the applications of PSO. The aim of
their study (Heryanto and Kusumoputro, 2021) was to propose an inner loop control algorithm
for UAV using a neural network–based DIC system. The experimental results
showed that the neural network–based DIC could follow the manoeuvres of the
testing trajectory dataset with excellent performance, as indicated by an
overall mean squared error (MSE). (Mehenge et al., 2023) work introduces a three-wheel holonomic
omnidirectional robot designed for mobile applications. This platform with
three omnidirectional wheels and DC motors, controlled by EMS 30A H-Bridge and
Arduino Mega 2560, it aligns kinematic calculations with mathematical models,
promising efficiency for diverse mobile manipulation robot applications. The main contribution of (Mohammed,
Al-Khafaji, and Abbas, 2023) paper is to develop an innovative algorithm
to accurately detect and identify the shape and color of objects and find their
location. The proposed algorithm utilizes the HSV color model to distinguish
between different object colors and shapes. After that, a series of filters are
applied to reduce the noise of these images to make the process of discovering
the shape and coordinates of the objects successful. (Wang et al. 2021) review a collision avoidance researches under unknown
environments for WMR including various types of controllers. In their approach (Pramujati
et al., 2023) introduces a model-based
control scheme consists of two systems for controlling the position of a
suspended cable-driven parallel robot. Three trajectories are generated to test
the compliance of the controller with its position. The error compensation scheme
is introduced to increase the positional accuracy of the previous controller,
especially on the z-axis. Williams and Wu (2010) have established a novel method of
obstacle-avoidance motion planning for mobile robots in dynamic environments,
wherein the obstacles are moving with general velocities and accelerations, and
their motion profiles are not preknown. A hybrid system is presented in which a
global deliberate approach is applied to determine the motion in the desired
path line (DPL).
Rusdinar et al. (2021) developed a mobile robot with a UVC light
system installed at the top and bottom to emit UVC light. This robot can be operated
automatically as it has a magnetic line sensor and employs a fuzzy inference
system algorithm for its movement. The experiment showed that UVC light has
good sterilization and disinfection performance.
Finally, it can be concluded that despite many methods are applied in the literature for designing the trajectory
tracking control strategy of the WMR for example: Fuzzy logic controller (Rahman, Hassan, and Ihsan, 2022), Adaptive Neuro-Fuzzy Inference System ;(ANFIS) (Tilahun
et al. 2023), Proportion integral differential (PID)(Saleh, Hussain, and Klim, 2018), linear quadratic regulator (LQR) (Uddin, 2018), model predictive control (MPC), etc, but they have drawbacks such as
large computational burden and long convergence time when dealing with under
actuated system. In addition, sliding model control (SMC) is
another effective method, but the chattering phenomenon limits its application.
In this
work, hybrid controllers based on kinematics and dynamics are designed to solve
the trajectory tracking problem of a four mecanum wheeled mobile robot. The
type of the optimal control is the Linear Quadratic Regulator controller (LQR).
LQR is applied to design the controlled torques required by actuators and parameters of LQR controller are tuned by
using Ant Colony Optimization (ACO).
In
this scenario, the mobile robot is viewed as a complete mechanism with the angular velocities of its wheels serving as inputs
and the
robot’s linear and angular velocities as
outputs. In this context
the Jacobian matrix of inverse
kinematics can be expressed as (Equation 1):
FMWMR inverse kinematic equation
in robot local coordinate system is expressed as below (Equation
2):
Where: is the Matrix of angular
velocities of all robot mecanum wheels. Taking
in account that
is the robot velocities in
global coordinate system,
equation of inverse kinematic can be written as follow in global coordinate
system (Equation
3):
Where matrix of robot local coordinates system rotation with
reference to global coordinates system, and will be presented (Equation 4):
The forward kinematic jacobian matrix is pseudo-inverse of (J)(Zeidis et al. 2019), its
formula was written as:
The forward kinematics equation
in robot local coordinates system is written (Equation 5):
In the Lagrange formulation, the dynamic model of the robot includes the motion of the system resulting from the inertia of the entire robot mechanism and external forces. As illustrated in Figure (1a), point C represents the centre of the robot’s local coordinate frame, and (D) is the mass centre of the entire robot mechanism.
Velocity of local coordinate system origin point of the FMWMR (point C) in robot local coordinate system is evaluated according to the theory in as (Equation 7):
Since the
robot cannot change its vertical position (z-axis), so its potential energy is
equal to zero. The kinetic energy of the whole robot mechanism includes the
kinetic energy of the four mecanum wheels and robot platform. In this
case L is only kinetic
energy of the robot and has been written as (Equation 9):
Where: mr: mass of robot
platform , mwi: mass of i wheel, Ir: Robot mass moment of
inertia about its centre of mass
point, Iwi: moment of inertia
of i wheel. The Lagrange equation derived from the total energy of the whole
robot will present the dynamic model and can be written as
(Equation 10):
The
general form of the robot dynamic equation can be written (Equation
11):
Mass and
inertia matrix
Matrix of carioles and
centripetal effect
Controller design for trajectory tracking
In this section, a control system with self-tuning parameters based on
an optimization algorithm is utilized for both robot models. The type of the
optimal control that is used in this work is the Linear Quadratic Regulator
controller (LQR). It is used to design the controlled torques generated by the
wheels motors. The parameters of the LQR controller are tuned by using Ant
Colony Optimization (ACO) and this matter is presented in the next subsections.
3.1. Linear quadratic regulator controller
(LQR)
LQR controller used in this work is adopted
to make an optimal control signal for the motors torques.
3.2. Ant colony optimization (ACO)
Pei,
Wang, and Zhang (2012) states
that, ACO type
of optimization is an intelligent heuristic algorithm which was developed in
1992 by Marco Dorigo which simulates from the ant foraging behaviour. The
communication between ants is relying on the pheromones and the pheromones are
proportional inversely with length of the path. During the searching of the
ants for the food in an unknown environment, ants have been moved threw a path
containing a high pheromone concentration. Concentration of pheromone is
directly proportional with the numbers of the ants that walking on this path.
Ants behaviours display the principle in which adopted to select an optimal path.
To enhance path planning efficiency, heuristic function and tabu list (tabuk)
are adopted into an artificial ant colony model. Within a time (t), ant k moves
from a current node i to an unvisited node j regarding the distance information
received from the target point and pheromone intensity during this path. In the
case of more than one unvisited node, the transition probability (
) between the nodes will be evaluated by the
ant K in accordance with the formula that shown (Equation 29) :
where U
represents the next node of ant k, is an expectation heuristic factor,
is a
pheromone heuristic factor,
is a pheromone concentration on the path ij at a period of time (t),
(t) is an expected heuristic functio a (Equation 30):
where is a Euclidean distance between
any two adjacent nodes. After finishing the path search by all ants, pheromone
was evaporated. The formula that describes the increasing of the pheromone on
the path (Equations 31 and 32):
where () represents the rate of the pheromone
evaporation, and (t) is the time of the iterations. Value of
depends on the pheromone addition which has been
done by an ant (K) after its movement on (ij) path during iteration time
(t). Mathematical model of
can be
defined as (Equation 33):
Where (N)
represents the intensity of the pheromone that added by the ant (K) and (LK)
represents the length of the path that was tracking by the ant (K) during one
iteration. There is no fixed rule to choose the ant's
number as well as the Max. number of iteration. The selection number is
considered to be acceptable because the higher number of iterations and ants
required more program execution time. Also, it is needed a computer with high
specifications.The basic
parameters for the ACO have been chosen as
follow:
Ants
Number: 30
In this work, ACO is adopted in selection of optimal values of (Q) and (R) matrices elements. In simulation work, a closed loop controller (Figure 2) has been implemented. This loop is a trajectory tracking controller based on minimizing the pose error to zero. We used LQR controller where the gains were obtained by using Anti Colony Optimization ACO to control the motors torques.
Figure 2 Controller architecture
The proposed controller has been
examined in two options of WMR movement. In first
option WMR follows a circular shape trajectory and in second option it follows
an infinity shape trajectory. The results have been simulated by using MATLAB
2019 software. The parameters of robot are taken as follow:
Figure 3 The first proposed circular Shape Trajectory followed
by the WMR
After two seconds of the WMR task starting, the
values of position trajectory error values are reduced to small value (ex=3.218 *10-5m) and (ey=
2.224*10-5m) in xo and yo directions,
respectively and remained almost at these values until the end of the
simulation time. The maximum orientation error is (= 0.103rad),
and convergent to zero after two seconds of the mobile robot movement. Figure
4a shows the robot linear and angular velocities in global coordinate system
during the circular trajectory. As shown
in Figure 4a the robot velocities behaviour is smooth during the simulation
time. The value of the linear velocities is fluctuated about ±0.4 m/s and robot
rotation velocity is 0.4 rad/s. Generated torques from robot mecanum wheels
motors can be evaluated at any time. The torques values have been shown in Figure
4b.
In the second option, the equations
of the infinity shape trajectory followed by the WMR are described as
(Equations 39 and 40):
Figure 4 Velocities and torques generated in all wheels when the WMR follows a circular shape trajectory
Figure 5 The second proposed Infinity Shape Trajectory followed by WMR
It has been seen, in the
two cases, simulation results show higher precision of trajectory tracking
because the position tracking errors (x,y) are less than 10-3m and acceptable comparing with most of
published researches.
Figure 6
Velocities and torques generated in all wheels when the WMR follows an infinity
shape trajectory
In this work, an
optimal control system is applied based on the kinematics and dynamics of the
four mecanum wheeled mobile robot for the trajectory tracking.
MATLAB software is used for results simulation of the proposed controller in
two cases. In the first case the robot followed a circular shape trajectory and
in the second case followed an infinity shape trajectory. The most important points are presented as: LQR controller with a
self-tuning parameters based on ACO are applied to control the robot motors
torques. In the first case,
the values of the trajectory errors in xo and yo
directions are ex=4.645*10-4m and ey = 7.382*10-5
m respectively and these values converge to zero after two seconds. In second case, maximum
absolute values of the trajectory error (ex), (ey) and are 0.05 (m) , 0.01 (m), and 0.08 (rad) respectively. After about three seconds, (ey) and
are reduced to small value -4.078 *10-4 (m) and 3.174*10-4
(rad) respectively, while (ex) is reduced to 5.263*10-4
(m) after about 15 sec. The magnitudes of
the torques are between ( ± 1.5 ) N/m.
Authors are pleased to express special appreciations and thanks to “Mechanical Engineering Department at University of Technology, Baghdad, Iraq” and “High School of Automation and Robotics at Peter the Great Saint Petersburg Polytechnic University” for their help and support during the research period.
Abed, M.S., Lutfy, O.F.,
Al-Doori, Q.F., 2021. A Review on Path Planning Algorithms for Mobile Robots. Engineering
and Technology Journal, Volume 39(5), pp. 804–820
Alwan, H.M., 2020. Kinematic Modeling and simulation of
Holonomic Wheeled Mobile Robot with Mecanum Wheels. Journal of Mechanical
Engineering Research and Developments, Volume 43(5), pp. 451–459
Amouri, A., Cherfia, A., Merabti,
H., 2022. Nonlinear Model Predictive Control of a Class of Continuum Robots
Using Kinematic and Dynamic Models. FME Transactions, Volume 50(2), pp.
339–350
Amudhan, A.N., Sakthivel, P.,
Sudheer, A.P., Kumar, T.S., 2019. Design of Controllers for Omnidirectional
Robot Based on the System Identification Technique for Trajectory
Tracking. Journal of Physics:
Conference Series, Volume 1240(1), p. 012146
Azar, A.T., Abed, A.M.,
Abdul-Majeed, F.A., Hameed, I.A., Jawad, A.J.M., Abdul-Adheem, W.R., Ibraheem,
I.K., Kamal, N.A., 2023. Design and Stability Analysis of Sliding Mode
Controller for Non-Holonomic Differential Drive Mobile Robots. Machines, Volume 11, p. 470
Chai, B.,
Zhang, K., Tan, M., Wang, J., 2024. An Optimal Robust Trajectory Tracking
Control Strategy for the Wheeled Mobile Robot. International Journal of
Control, Automation and Systems, Volume 22(3), pp. 1050–1065
Chen, G., Liu, J., 2019. Mobile
Robot Path Planning Using Ant Colony Algorithm and Improved Potential Field
Method. Computational Intelligence and Neuroscience Journal, Volume 12,
pp. 1–10
Cui, Q.Z., Li, X., 2012.
Backstepping Control Design on the Dynamic of Omni-Directional Mobile
Robot. Journal of Applied Mechanics
and Materials, Volume 203, pp. 51–56
El-Shorbagy, M.A., Hassanien,
A.E., 2018. Particle Swarm Optimization from Theory to Applications. International Journal of
Rough Sets and Data Analysis, Volume 5(2), pp. 1–14
Gao, Z., Yang, Y., Du, Y., Zhang,
Y., Wang, Z., Xu, W., 2017. Kinematic Modeling and Trajectory Tracking Control
of a Wheeled Omni-directional Mobile Logistics Platform. In: Asia-Pacific
Engineering and Technology Conference (APETC), pp. 169–175
Hasan, S.F., Alwan, H.M., 2022.
Local Path Planning of a Four Mecanum Wheeled Mobile Robot Based on New
Modified Ultrasonic Sensors with Experimental Implementation. International
Journal of Mechanical Engineering, Volume 7(1), pp. 4621–4627
Hasana, S.F., Alwan, H.M., 2021.
Modelling and Control of Wheeled mobile Robot with Mecanum Wheels. Engineering and Technology journal,
Volume 39(A), pp. 779–789
Heryanto, M.A., Kusumoputro, B.,
2021. Attitude and Altitude Control of Quadcopter Maneuvers
using Neural Network–Based Direct Inverse Control. International
Journal of Technology, Volume 12(4), pp. 843–853
Hussein, R.M., 2023. Design a New
Hybrid Controller Based on an Improvement Version of Grey Wolf Optimization for
Trajectory Tracking of Wheeled Mobile Robot. FME Transactions, Volume
51(2), pp. 140–148
Keek, J.S., Loh, S.L., Chong, S.H., 2018. Fractional-Order
Proportional-Integral (FOPI) Controller for Mecanum-Wheeled Robot (MWR) in
Path-Tracking Control. International Journal of Mechanical Engineering and
Technology (IJMET), Volume 9(11), pp. 325–337
Khadanga,
R.K., Padhy, S., Panda, S., Kumar, A., 2018. Design and Analysis of Tilt Integral Derivative Controller for Frequency
Control in an Islanded Microgrid: A Novel Hybrid Dragonfly and Pattern Search
Algorithm Approach. Arabian Journal
for Science and Engineering, Volume 43 (6), pp. 1–12
Malayjerdi,
E., Kalani, H., Malayjerdi, M., 2018. Self-Tuning
Fuzzy PID Control of a Four-Mecanum Wheel Omni-directional Mobile Platform. 26th
Iranian Conference on Electrical Engineering(ICEE), Volume 2018, pp.
816–820
Mehenge, R., Satoskar, N., Shidhore, A., Arshath, N.M., 2023. Kinematic and Optimal design of a Three-wheeled Holonomic
Omnidirectional Robot Platform for Mobile Manipulation Tasks. Global
Journal of Engineering and Technology Advances, Volume 17(1), pp. 45–54
Mohammed, M.M., Al-Khafaji, M.M.,
Abbas, T.F., 2023. Smart Robot Vision for A Pick and Place Robotic System. Engineering
and Technology Journal, Volume 41(6), pp. 756–770
Morales, S., Magallanes, J.,
Delgado, C., Canahuire, R., 2018. LQR Trajectory Tracking Control of an
Omnidirectional Wheeled Mobile Robot. In: IEEE 2nd Colombian
Conference on Robotics and Automation (CCRA), pp. 1–5
Pei, Y., Wang, W., Zhang, S., 2012. Basic Ant Colony
Optimization. In: International
Conference on Computer Science and Electronics Engineering, Hangzhou,
pp. 665–667
Pramujati, B., Syamlan, A.T.,
Nurahmi, L., Tamara, M.N., 2023. Study on the Application of
Model-based Control Algorithm for a Suspended Cable-Driven Parallel
Robot. International Journal of Technology. Volume 14(4), pp. 854–866
Rahman, A., Hassan, N., Ihsan,
S.I., 2022. Fuzzy Logic Controlled Two Speed Electromagnetic Gearbox
for Electric Vehicle. International Journal of Technology. Volume 13(2), pp.
297–309
Rusdinar, A., Purnama, I., Fuadi, A.Z., Adiluhung, H., Wicaksono, M.,
Risnanda, Ningrum, R.A., 2021. Automated Ultraviolet C Light Mobile Robot for
Room Sterilization and Disinfection. International Journal of Technology,
Volume 12(4), pp. 854–864
Saleh, A., Hussain, M., Klim, S.,
2018. Optimal Trajectory Tracking Control for A Wheeled Mobile
Robot Using Fractional Order PID Controller. Journal of University of
Babylon, Vvolume 26, pp. 292–306
Song, B.,
Tang, S., Li, Y., 2024. A New
Planning Integrating Improved ACO and DWA Algorithms for Mobile Robots in
Dynamic Environments. Mathematical and Biosciences and Engineering Journal,
Volume 21(2), pp. 2189–2211
Sun, Z., Xie, H., Zheng, J., Man,
Z., He, D., 2020. Path-following Control of Mecanum-Wheels Omnidirectional
Mobile Robots Using Nonsingular Terminal Sliding Mode. Mechanical Systems
and Signal Processing, Volume 147, p. 107128
Tilahun, A.A., Desta, T.W., Salau, A.O., Negash, L.,
2023. Design of an Adaptive Fuzzy Sliding Mode Control with Neuro-Fuzzy System
for Control of a Differential Drive Wheeled Mobile Robot. Cogent Engineering,
Volume 10(2), p. 2276517
Uddin, N., 2018. Trajectory
Tracking Control System Design for Autonomius Two-Wheeled Robot. Journal Infotel, Volume 10(3), pp. 90–97
Wang, C., Liu, X., Yang, X., Hu,
F., Jiang, A., Yang, C., 2018.
Trajectory Tracking of an Omni-Directional Wheeled Mobile Robot Using a Model
Predictive Control Strategy. Applied Science, Volume 8(2), p. 231
Wang, H., Ma, X., Zhu, L., 2022. Obstacle Avoidance Path Planning of Mobile Robot Based
on Improved DWA. Journal of Physics: Conference Series, Volume
2383(1), p. 012098
Wang, Y., Li, X., Zhang, J., Li,
S., Xu, Z., Zhou, X., 2021. Review of Wheeled Mobile Robot Collision Avoidance
under Unknown Environment. Science Progress Journal, Volume 104(3), pp.
1–26
Williams, R.L., Wu, J., 2010.
Dynamic Obstacle Avoidance for An Omnidirectional Mobile Robot. Journal of
Robotics, Volume 2010, p. 901365
Yuan, Z., Tian, Y., Yin, Y.,
Wang, S., Liu, J., Wu, L., 2019. Trajectory Tracking Control of a Four Mecanum
Wheeled Mobile Platform: an Extended State Observer-Based Sliding Mode
Approach. IET Control Theory & Applications, Volume 14(3), pp.
415–426
Yuan, Z., Tian, Y., Yin, Y.,
Wang, S., Liu, J., Wu, L., 2019. Trajectory Tracking Control of a Four Mecanum
Wheeled Mobile Platform: an Extended State Observer-Based Sliding Mode
Approach. IET Control Theory & Applications, Volume 14(3), pp.
415–426
Zeidis, I., Zimmermann, K., 2019.
Dynamic of Four Wheeled Mobile Robot with Mecanum Wheels. Journal of Applied Mathematics and
Mechanics, Volume 3, pp. 1–22
