Vehicle Localization Based On IMU, OBD2, and GNSS Sensor Fusion Using Extended Kalman Filter
Published at : 31 Oct 2023
Volume : IJtech
Vol 14, No 6 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i6.6649
Teoh, T.S., Em, P.P., Ab Aziz, N.A.B., 2023. Vehicle Localization Based On IMU, OBD2, and GNSS Sensor Fusion Using Extended Kalman Filter. International Journal of Technology. Volume 14(6), pp. 1237-1246
| Tai Shie Teoh | Faculty of Engineering and Technology, Multimedia University, Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia |
| Poh Ping Em | Faculty of Engineering and Technology, Multimedia University, Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia |
| Nor Azlina Binti Ab Aziz | Faculty of Engineering and Technology, Multimedia University, Jalan Ayer Keroh Lama, 75450 Melaka, Malaysia |
Multiple systems have been developed to identify
drivers’ drowsiness. Among all, the vehicle-based driver drowsiness detection
system relies on lane lines to determine the lateral position of the vehicle
for drowsiness detection. However, the lane lines may fade out, affecting its
reliability. To resolve this issue, a vehicle localization algorithm based on
the Inertial Measurement
Unit
(IMU), Global Navigation
Satellite System
(GNSS), and Onboard Diagnostics (OBD2) sensors is introduced. Initially, the kinematic bicycle
model estimates the vehicle motion by using inputs from the OBD2 and IMU.
Subsequently, the GNSS measurement is used to update the vehicle motion by
applying the extended Kalman filter. To evaluate the algorithm’s performance,
the tests were conducted at the residential area in Bukit Beruang, Melaka and
Multimedia University Melaka Campus. The results showed that the proposed
technique achieved a total root-mean-square error of 3.892 m. The extended
Kalman filter also successfully reduced the drift error by 40 – 60%.
Nevertheless, the extended Kalman filter suffers from the linearization error.
It is recommended to employ the error-state extended Kalman filter to minimize
the error. Besides, the kinematic bicycle model only generates accurate
predictions at low vehicle speeds due to the assumption of zero tire slip
angles. The dynamic bicycle model can be utilized to handle high-speed driving
scenarios. It is also advised to integrate the LiDAR sensor since it offers
supplementary position measurements, particularly in GNSS-denied environments.
Lastly, the proposed technique is expected to enhance the reliability of the
vehicle-based system and reduce the risk of accidents.
Extended kalman filter; Kinematic bicycle model; Vehicle localization
Road accidents in Malaysia have grown from 462420
cases in 2012 to 567520 cases in 2019 (Ministry of
Transport Malaysia, 2022). It is believed that tiredness causes 20% of
all traffic accidents (The Star, 2022). The
factors that contribute to the driver’s drowsiness encompass the circadian
rhythm, sleep homeostasis, and time on task (Zainy et
al., 2023; Zuraida, Wijayanto, and Iridiastadi, 2022). The ability
to deal with stress also plays an important role in drowsiness development.
Driving as work might be stressful for some bus drivers, accelerating their
level of drowsiness (Zuraida and Abbas, 2020).
Therefore, researchers have explored various approaches to assess driver
drowsiness, including monitoring drivers' physiological signals, facial
expressions, and driving behaviors.
Out of
these 3 categories of Driver Drowsiness Detection (DDD) systems, the
vehicle-based measure monitors the Steering Wheel Angle (SWA), acceleration, or Standard Deviation of the Lateral Position (SDLP) to detect any
abnormal driver’s conditions. A drowsy driver may demonstrate the
characteristics of sluggish steering, slow change in acceleration, and
frequently switching lanes while driving (Shahverdy
et al., 2020; Vinckenbosch et al., 2020). Besides, the
vehicle-based measure also has several limitations. First of all, it is
difficult for the system to extract precise drowsiness signals (Pratama, Ardiyanto, and Adji, 2017). For example,
the Lane Departure Warning System detects lane lines by incorporating a
forward-looking camera behind the vehicle windshield. It cannot determine
whether the vehicle has deviated from the lane if the lane lines marked on the
road have faded out. Besides, the quality of the images can be easily affected
by tree shadow and uneven illumination (Chen et
al., 2020). To resolve the issue of low reliability of the
vehicle-based DDD system, a method that can monitor the position of the vehicle
in the lane without depending on the existing road infrastructure and the
surrounding environment is desirable.
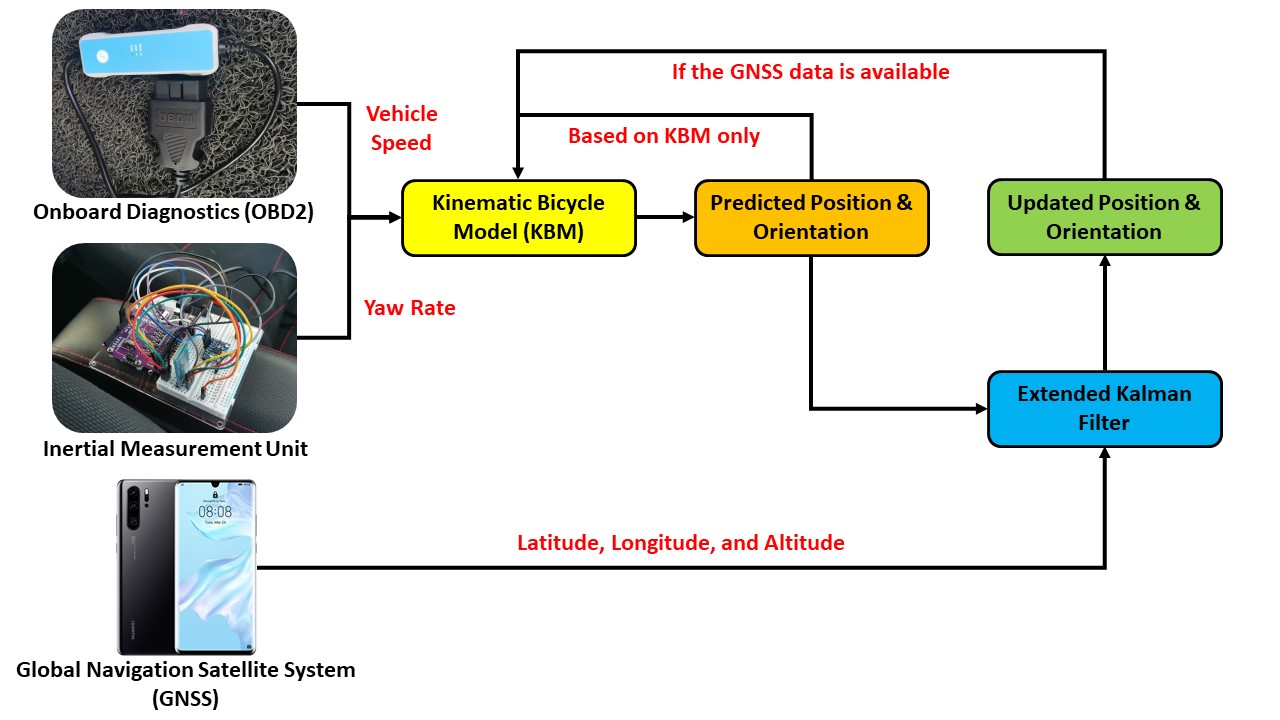
The flowchart of the vehicle localization algorithm is illustrated in Figure 1. Initially, the KBM is used to estimate the vehicle motion. Two inputs are required which are the vehicle speed and the yaw rate. To acquire the vehicle speed, it is necessary to connect the Controller Area Network (CAN) bus data logger to the OBD2 connector of the vehicle. Additionally, the yaw rate can be obtained by placing the IMU at the Center of Gravity (COG) of the vehicle. Next, whenever the GNSS data is available, it will be used to update the estimated position and orientation of the vehicle by utilizing the Extended Kalman Filter (EKF). The GNSS data is obtained by using the GNSS receiver of the Android smartphone. If the GNSS data is lost when the vehicle is driving inside the tunnel, the vehicle localization will be solely dependent on the KBM.
Figure 1 The flowchart of the vehicle localization algorithm
2.1. Experimental Setup
The vehicle localization algorithm was developed in
open source language Python with all supported libraries (PySerial, Socket, and
Python-CAN). The instrumented vehicle used in this experiment is Perodua Axia
(SE) 2014. It has a wheelbase of 2455 mm and a trackwidth of 1410 mm. To
extract the vehicle speed, the Korlan USB2CAN adapter was utilized to connect
the computer to the CAN bus via the OBD2 connector. The CAN ID 0x0b0 contains
information about the reading of the speedometer. It is given as the first byte
of the CAN message. To decode the CAN data into the actual vehicle speed, both
the CAN data and GNSS speed values were recorded at various speeds ranging from
10 to 70 km/hr, relative to the speedometer. This is shown in Table 1.
Table 1 The recorded CAN data and GNSS speed values at different speedometer
readings from 10 – 70 km/hr
|
Speedometer Reading (km/hr) |
CAN data |
GNSS Speed Value (km/hr) |
|
10 |
7 |
10 |
|
20 |
14 |
19 |
|
30 |
21 |
29 |
|
40 |
28 |
38 |
|
50 |
35 |
48 |
|
60 |
42 |
57 |
|
70 |
49 |
67 |
From Table 1, it can be observed that
the CAN data can be converted to the speedometer reading via a constant factor
of 1.429. Moreover, there is a 5% difference between the speedometer reading
and the GNSS speed value. This is because most automotive manufacturers will
calibrate their speedometers to allow for 5% - 10% higher readings due to the
requirement of traffic safety. Thus, 1.429 is divided by 1.05 to obtain the
final conversion factor of 1.361. The value from the CAN bus was multiplied by
this factor to retrieve the actual vehicle speed.
Besides, the IMU was installed at the
COG of the vehicle (behind the handbrake), assuming the COG is located at the
center of the wheelbase and the center of the trackwidth. Additionally, IMU
uses MPU-6050 (3-axis accelerometer and 3-axis gyroscope) to extract the yaw
rate of the vehicle. Once the gyroscope data was received by Arduino Uno from
MPU-6050, it was sent to the computer through the Bluetooth Serial Port
Protocol (SPP) module HC-05. Moreover, an Android smartphone (Huawei P30)
served as the GNSS receiver for measuring the vehicle's present latitude,
longitude, and altitude. The Python code was executed on the Android platform
using QPython 3L, a Python-integrated development environment. Once the vehicle
position was acquired, it was sent to the computer through the wireless
network. Finally, the vehicle speed, yaw rate, and GNSS data were collected at
different sampling frequencies. For example, the Korlan USB2CAN adapter
collects the vehicle speed from the CAN bus at 50 Hz (every 0.02 s) while the
IMU reports the angular velocity at 10 Hz (every 0.1 s). Besides, the GNSS
receiver retrieves the position of the vehicle at 1/3 Hz (every 3 s).
Therefore, the resampling was performed to synchronize the time series
observations. In this project, down-sampling was applied to resample the data
into a 0.2 s window. The values of the data points that fell into each 0.2 s
window were averaged to generate a single aggregated value.
2.2. Kinematic Bicycle Model
(KBM)
The bicycle model of the vehicle is depicted in Figure 2.
Figure 2 Kinematic
Bicycle Model (Kong et al., 2015)
In the bicycle model, both left and
right wheels at the front and rear axles of the vehicle can be represented as a
single wheel at points A and B respectively. The symbols and
, respectively,
denote the steering angles for the front and rear wheels. The rear steering
angle can be changed to zero because the model was developed under the
assumption of front-wheel steering. Furthermore, point C is where the COG of
the vehicle is situated.
and
respectively,
are distances between points A and B and the COG of the car. Assuming the
vehicle is having planar motion, the vehicle motion can be described by 3 state
variables:
represents
the coordinate of the vehicle in a global (inertial) reference frame while
defines
the orientation of the vehicle (also known as heading angle or yaw angle). The
model requires 2 inputs to fully describe the vehicle motion. The first input
is the velocity at the COG of the vehicle which is denoted as
in Figure 2.
The velocity makes an angle
with
the longitudinal axis of the vehicle. This angle is known as the vehicle slip
angle. Moreover, the second input of the model is the yaw rate
The
yaw rate is also equivalent to the angular velocity measured by the IMU about
the vertical axis at the COG of the vehicle
The
vehicle position and orientation
can be calculated by using Equations (1), (2), and (3) based on
the explicit Euler method.
is
referred to as the time step size.
2.3. Extended Kalman Filter
(EKF)
EKF is a powerful prediction
algorithm that is used to provide estimates of some unknown variables based on
a series of measurements observed over time. It is selected in this study
because it is not computationally intensive and simple to implement. It consists
of 2 stages: prediction and update. In the prediction stage, the EKF predicts
the next state estimate by
using the previous updated state estimate
Once
the measurement is observed, it is used to update the current state estimate,
outputting
The EKF algorithm
is summarized from Equations (8) until (12) where I is the identity matrix:
From the above equations,
the motion model is represented by The term
is referred to as the
input vector whereas
is denoted as the process
noise which has a (zero mean) normal distribution with a constant covariance
Process noise is used to
describe the uncertainty of the motion model. The
equations from (1) to (7) can be rearranged into
the matrix form, producing the vehicle state vector
The vehicle state vector, input vector, process
noise covariance matrix, and motion model are given
in Equations (13), (14), (15), and (16). The terms
and
in Equation (15) are known as the variance of the
velocity and yaw rate respectively.
From Equation (9), the terms are
known as the motion model Jacobians. They can be calculated via Equations (19)
and (20):
Besides, from Equation (10), are called the measurement model
Jacobians. They can be computed by applying Equations (21) and (22):
The data logging of x and y positions of
the vehicle was conducted at 2 locations: the residential area in Bukit
Beruang, Melaka (location A) and Multimedia University Melaka Campus (location
B). The root-mean-square error (RMSE) of the position of the vehicle was
calculated for both KBM and EKF by treating the position of the vehicle
received from the GNSS as the ground truth. The results are shown in Table 2. Additionally, the paths mapped by the KBM and EKF as well
as the actual paths traveled by the vehicle, collected from the GNSS are
visualized on Google Maps. These are shown in Figure 3 for locations A and B.
Table 2 The Root-Mean-Square Error (RMSE) of the position of the vehicle for both
KBM and EKF
|
Vehicle Localization Techniques |
Root-Mean-Square Error (RMSE) | |||
|
Location A |
Location B | |||
|
|
|
|
| |
|
KBM |
11.898 |
8.918 |
8.052 |
4.856 |
|
EKF |
4.469 |
2.889 |
2.584 |
2.911 |
Figure 3 The paths mapped by the KBM, EKF,
and GNSS: (a) location A; (b) location
B
Firstly, from Figure 3a, it is noticeable that the path estimated by the KBM (blue line) in location A has drifted away from the actual path after the vehicle passes through the sharp 90o corner. A similar issue also occurs in location B when the vehicle passes through the entrance of MMU and the roundabout, as illustrated in Figure 3b. The drift error in both locations can be caused by the numerical approximation (Explicit Euler method) when calculating the position and orientation of the vehicle. Secondly, the EKF successfully decreases the drift error incurred by the KBM by updating the predicted position and orientation with the GNSS data. Table 2 illustrates that the EKF has significantly reduced the RMSE of the KBM by approximately 40% to 60%. In order to assess the performance of the proposed algorithm in comparison to other existing techniques, the total RMSE was computed by using Equation (23):
The comparison between the existing
techniques and the proposed technique in terms of total RMSE is shown in Table 3. The sensor data, motion models, and
prediction algorithms used by each technique are also illustrated.
Table 3 The comparison between the existing techniques and the proposed technique
Note
that the existing studies do not provide a universal definition for the
classification of the accuracy of the vehicle localization algorithm.
Therefore, to compare the proposed method with the existing techniques,
positioning accuracy is classified into 3 distinct levels based on Williams et al.
(2012). They are which-road which-lane
and where-on-the-lane
accuracy.
From Table 3, it can be seen that the proposed method only
achieves which-road accuracy in vehicle localization compared to other authors.
This can be due to several reasons. First of all, the EKF linearizes the
non-linear motion and measurement models to estimate the mean and covariance of
the state. For highly non-linear systems, the linearization error can be very
large. Thus, some authors have utilized the Error State
Extended Kalman Filter (ES-EKF) to estimate the error state instead of
the full vehicle state because the error behaves much closer to a linear
behavior compared to the vehicle state. To clarify this, consider a non-linear
motion model
as
shown in Equation (24), where
represents
the rate of change of the state vector
Note that the input and process noise are
ignored for simplicity.
This
paper presented a vehicle localization algorithm that relies on the combination
of IMU, GNSS, and OBD2 sensors. It will be utilized on the DDD system in future
to extract the SDLP from the vehicle and subsequently evaluate the driver's
drowsiness. Initially, the KBM predicts the position and orientation of the
vehicle by using the vehicle speed and yaw rate received from the OBD2 and IMU
respectively. Next, the EKF updates the predicted position and orientation with
the GNSS data. From the tests conducted at 2 distinct locations, it was found
that the proposed technique attained a total RMSE of 3.892 m. Besides, the
proposed technique greatly alleviated the drift error owing to the numerical
approximation in the KBM by 40 – 60%. Nonetheless, the EKF suffers from the
linearization error. Since the error behaves much closer to the linear
behavior, ES-EKF could be used to produce a more accurate state estimate.
Moreover, the KBM is only able to produce accurate predictions at low vehicle
speeds because of the assumption of zero tire slip angles. Hence, it is
suggested to incorporate the DBM into the motion model to handle the high-speed
driving scenario. Finally, the proposed technique only relies on the GNSS data
for measurement updates. It is recommended to include the LiDAR sensor to
provide additional position measurements, especially in GNSS-denied
environments.
The
Malaysian Ministry of Higher Education (MOHE) for Fundamental Research Grant
Scheme (FRGS/1/2022/TK0/MMU/02/13), the TM R&D Fund (MMUE/220021), and
Multimedia University (MMU) IR Fund (Grant No. MMUI/220032) provided funding
for the research described in this paper.
Aqel, M.O.A., Marhaban, M.H., Saripan, M.I., Ismail, N.B., 2016. Review of visual odometry: types, approaches,
challenges, and applications. SpringerPlus, Volume 5(1), pp. 1–26
Chen, W., Wang, W., Wang, K., Li, Z., Li,
H., Liu, S., 2020. Lane
Departure Warning Systems
and Lane Line Detection
Methods Based on Image Processing
and Semantic Segmentation?: A Review. Journal
of Traffic and Transportation Engineering (English Edition),
Volume 7(6), pp.
748–774
Dai, K. Sun, B., Wu, G.,
Zhao, S., Ma, F., Zhang, Y., Wu, J., 2023. LiDAR-Based Sensor Fusion SLAM and
Localization for Autonomous Driving Vehicles in Complex Scenarios. Journal of Imaging,
Volume 9(2), p. 52
Gao, L. Xiong, L., Xia,
X., Lu, Y., Yu, Z., Khajepour,
A., 2022. Improved Vehicle Localization Using On-Board
Sensors and Vehicle Lateral Velocity. Institute
of Electrical and Electronics Engineers (IEEE) Sensors Journal,
Volume 22(7),
pp. 6818–6831
Gu, Y., Hsu, L., Kamijo, S., 2015. Passive
Sensor Integration for Vehicle Self-Localization in Urban Traffic Environment. Sensors,
Volume 15(12),
pp. 30199–30220
Kong, J. Pfeiffer, M.,
Schildbach, G., Borrelli, F., 2015. Kinematic
and Dynamic Vehicle Models
for Autonomous Driving Control
Design. Institute of Electrical
and Electronics Engineers (IEEE) Intelligent Vehicles Symposium (IV), pp.
1094–1099
Madyastha, V.K., Ravindra, V., Mallikarjunan, S., Goyal, A., 2011. Extended
Kalman Filter vs. Error State
Kalman Filter for Aircraft Attitude Estimation. In: American Institute of Aeronautics and
Astronautics (AIAA) Guidance, Navigation, and Control Conference, p. 6615
Meng, X., Wang, H., Liu, B., 2017. A Robust
Vehicle Localization Approach Based on GNSS/IMU/DMI/LiDAR Sensor Fusion
for Autonomous Vehicles. Sensors,
Volume 17(9), p. 2140
Min, H., Wu, X., Cheng, C., Zhao, X., 2019. Kinematic
and Dynamic Vehicle Model-Assisted Global Positioning Method for Autonomous
Vehicles with Low-Cost GPS/Camera/In-Vehicle Sensors. Sensors,
Volume 19(24),
p. 5430
Ministry of Transport
Malaysia, 2022. Road Accidents and Fatalities in Malaysia.
Available at: https://www.mot.gov.my/en/land/safety/road-accident-and-facilities, Accessed on August 17, 2022
Ng, K.M. Abdullah, S.A.C.,
Ahmad, A., Johari, J., 2020. Implementation
of Kinematics Bicycle Model for Vehicle Localization using Android Sensors. In: 2020 11th Institute of Electrical
and Electronics Engineers (IEEE) Control and System Graduate Research
Colloquium (ICSGRC), pp.
248–252
Pratama, B.G., Ardiyanto,
I., Adji, T.B., 2017. A
Review on Driver Drowsiness
Based on Image, Bio-signal,
and Driver Behavior. In:
2017 3rd International Conference on Science and
Technology-Computer (ICST), pp. 70–75
Sardana, R., Karar, V., Poddar, S., 2023. Improving
visual odometry pipeline with feedback from forward and backward motion
estimates. Machine
Vision and Applications, Volume 34(2), p. 24
Shahverdy, M., Fathy, M., Berangi, R., Sabokrou, M., 2020. Driver
behavior detection and classification using deep convolutional neural networks. Expert Systems with Applications,
Volume 149, p.
113240
Suwandi, B., Pinastiko,
W.S., Roestam, R., 2019. On
Board Diagnostic-II (OBD-II)
Sensor Approaches for the Inertia Measurement Unit (IMU) and Global Positioning
System (GPS) Based Apron Vehicle Positioning System. In: 2019
- International Conference on Sustainable Engineering and Creative Computing (ICSECC), pp.
251–254
Toy, I., Durdu, A., Yusefi, A., 2022. Improved
Dead Reckoning Localization using Inertial
Measurement Unit (IMU) Sensor. In: 2022 15th
International Symposium on Electronics and Telecommunications (ISETC), pp.
1–5
Vinckenbosch, F.R.J., Vermeeren, A., Verster, J.C.,
Ramaekers, J.G., Vuurman, E.F., 2020.
Validating Lane Drifts as a Predictive Measure of Drug or Sleepiness
Induced Driving Impairment. Psychopharmacology,
Volume 237, pp.
877–886
Williams, T., Alves, P., Lachapelle, G., Basnayake, C., 2012. Evaluation
of Global Positioning System (GPS)-based Methods
of Relative Positioning for Automotive Safety Applications. Transportation Research
Part C: Emerging Technologies, Volume 23, pp. 98–108
Yanase, R., Hirano, D., Aldibaja, M., Yoneda,
K., Suganuma, N., 2022. LiDAR-and
Radar-Based Robust Vehicle Localization with Confidence Estimation of Matching
Results. Sensors,
Volume 22(9),
pp. 1–20
Yang, W., Gong, Z., Huang, B., Hong, X., 2022. Lidar
With Velocity?: Correcting Moving Objects Point Cloud Distortion From
Oscillating Scanning Lidars by Fusion With Camera. Institute
of Electrical and Electronics Engineers (IEEE) Robotics and Automation Letters,
7(3), pp. 8241–8248
Zainy, M.L.S., Pratama,
G.B., Kurnianto, R.R., Iridiastadi, H., 2023. Fatigue Among Indonesian Commercial Vehicle
Drivers: A Study Examining Changes in Subjective Responses and Ocular
Indicators. International
Journal of Technology, 14(5), pp. 1039–1048
Zhang, J., Singh, S., 2014. LOAM:
Lidar Odometry and Mapping in Real-time. In: Robotics: Science and Systems,
Volume 2(9), pp. 1–9
Zuraida, R., Abbas, B.S., 2020. The
Factors Influencing Fatigue Related
to the Accident of Intercity Bus Drivers
in Indonesia. International
Journal of Technology, Volume 11(2), pp. 342–352
Zuraida, R., Wijayanto, T., Iridiastadi, H., 2022. Fatigue
During Prolonged Simulated
Driving: An Electroencephalogram Study. International
Journal of Technology, Volume 13(2), pp. 286–296
