Fuel Costs Optimization for Long-Haul Flight with Refueling Layovers
Published at : 24 Dec 2024
Volume : IJtech
Vol 15, No 6 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i6.7285
Leenawong, C., Ritthipakdee, A., 2024. Fuel Costs Optimization for Long-Haul Flight with Refueling Layovers. International Journal of Technology. Volume 15(6), pp. 1602-1612
| Chartchai Leenawong | School of Science, King Mongkut's Institute of Technology Ladkrabang, Bangkok, 10520 Thailand |
| Amarita Ritthipakdee | Faculty of Science and Technology, Phranakhon Rajabhat University, Bangkok 10220, Thailand |
This study introduced a mathematical model aimed at optimizing fuel costs for long-haul flights, particularly those requiring refueling. The primary objective was to minimize fuel expenses by considering key factors such as flight routes, aircraft types, refueling points, and refueling quantities. The proposed solution used a 0-1 mixed-integer linear programming (MILP) model, supported by auxiliary variables, to effectively manage the constraints of this optimization problem. The MILP model also considered differences in fuel costs at refueling points, including the departure airport. For validation, a case study was conducted involving a long-haul flight from airport AAA to DDD, with refueling options at airports BBB and CCC. The model effectively determined the most economical flight route, assessed the necessity of refueling, and calculated the required fuel amounts at each refueling location. In summary, this study demonstrated that the proposed model could successfully address the challenges of optimizing fuel costs in long-haul flight.
0-1 mixed integer programming; Long-haul flight; Optimization; Refueling
Air transport plays a big role in Thailand's economy, acting as a key transportation method for goods and passengers (Office of Industrial Economics, 2021). Its efficiency and ease of use attract many travelers (Wensveen, 2015), creating significant economic benefits for aviation and related industries, such as logistics, tourism, and trade.
Managing operational costs for a long-haul flight that requires refueling presents a critical challenge due to the complexities involved in fuel management and strategic refueling decisions (Hahn, 2012). Fuel costs account for a large proportion of airline operational expenses, directly influencing financial performance (Park and O'Kelly, 2018). Consequently, airlines must optimize fuel consumption and select cost-effective refueling points to balance costs minimization with maintaining an adequate fuel supply. The volatile nature of fuel costs further complicates this process, suggesting the need for an effective model to mitigate financial risks caused by price fluctuations (Hsu and Eie, 2013).
Hedging has proven to be an effective tool for mitigating the volatility of fuel costs. By using financial instruments such as futures, options, and swaps, airlines can stabilize costs and revenue, even during periods of high prices (Swidan, Merkert, and Kwon, 2019; Cobbs and Wolf, 2004). This risk management tool helps airlines safeguard against market unpredictability. Previous investigations also showed a direct correlation between rising fuel costs and increased airfare, which negatively affected passenger demand and profitability (Gayle and Lin, 2020). Additionally, delays in ticket payments and uncertainties at key airline hubs make planning flight more complicated, requiring attention to fuel needs, payload limits, and safety considerations (Singh and Sharma, 2015; Wongwiwat, 2014).
Fuel costs are critical in fleet management and aircraft design. Manufacturers focus on improving performance to cut down fuel use and lower operating costs (Elzayady and Elghandour, 2021; Oguntona et al., 2016), enabling airlines to stay competitive (Qiu, Wang, and Qian, 2023). Fleet planning involves factors like fuel price changes, air traffic fees, and infrastructure expenses. For example, turboprop planes cost less per passenger than regional jets (Smirti and Hansen, 2009), making them an alternative for airlines. Also, practices like fuel tankering and ferrying allow airlines to take advantage of price differences between refueling stations (Hubert et al., 2015; Kheraie and Mahmassani, 2012). Improvements in noise prediction have also shaped aircraft designs by addressing noise and environmental regulations (Kusumalestari et al., 2024).
An optimization model has been created to solve fuel consumption and flight route problems. In the context of aircraft routing with air refueling, both heuristic and exact algorithms have been designed to lower costs while ensuring enough fuel (Kannon et al., 2014). One innovative approach, formation flight, has been shown to reduce fuel consumption by 7.7% and operating costs by 2.6% for long international flight (Xu et al., 2014). A graph-based model is another option for optimizing routes when winds change, but it uses a lot of computer power (Bijlsma, 2009). Another method, simulated annealing for mixed airspace, helps make routes shorter and lowers fuel use (Aydo?an and Cetek, 2022). Also, a bi-level optimization framework in formation flight worked well for cutting drag and saving fuel (Xu et al., 2012).
The focus on fuel efficiency and the environment makes the models more necessary. They are especially helpful for cutting CO2 emissions while keeping operations working smoothly (Doulgeris, Kirner, and Laskaridis , 2011). This focus highlights the importance of advanced optimization model in airline operations, which also address environmental issues such as air pollution and waste management (Kondili, 2005). In transportation, such as locomotive assignment, optimization is used to allocate resources efficiently under operational constraints (Piu and Speranza, 2014). Similar models are also applied in fields like telecommunications, computer science, and bioinformatics for solving complex issues (Alba et al., 2009).
Recent advancements in optimization have shown its versatility in resource management across multiple industries. For example, mathematical optimization model such as linear programming (LP) have proven effective in solving production-related challenges (Matousek and Gärtner, 2007). Applications include parking management (Nahry, Tjahjono, and Brotoadi, 2015) and manufacturing, where space allocation helps reduce congestion and production costs (Rosyidi, Fatmawati, and Jauhari, 2016). In environmental efforts, mixed-integer nonlinear programming supports bittern recovery (Widodo et al., 2023), while robust optimization aids in managing plastic waste in Jakarta (Ardi et al., 2023). For airlines, optimization helps with gate assignments ( Zhang and Klabjan, 2017), resolves air traffic conflicts (Alonso-Ayuso, et al., 2013), and minimizes delays for better profits (McCarty and Cohn, 2018).
An LP framework had an objective function and constraints, which were based on a finite number of variables. A 0-1 MILP, which was like LP but more specific (Sioshansi and Conejo, 2017), had variables that were either 0 or 1. These binary variables were important for deciding flight routes, types of aircraft, and where to refuel. Additionally, auxiliary variables were used to enforce the constraints. The 0-1 MILP began by identifying important factors that affect fuel costs, and then provided a detailed explanation of the proposed mathematical framework.
2.1.Identifying Relevant Factors
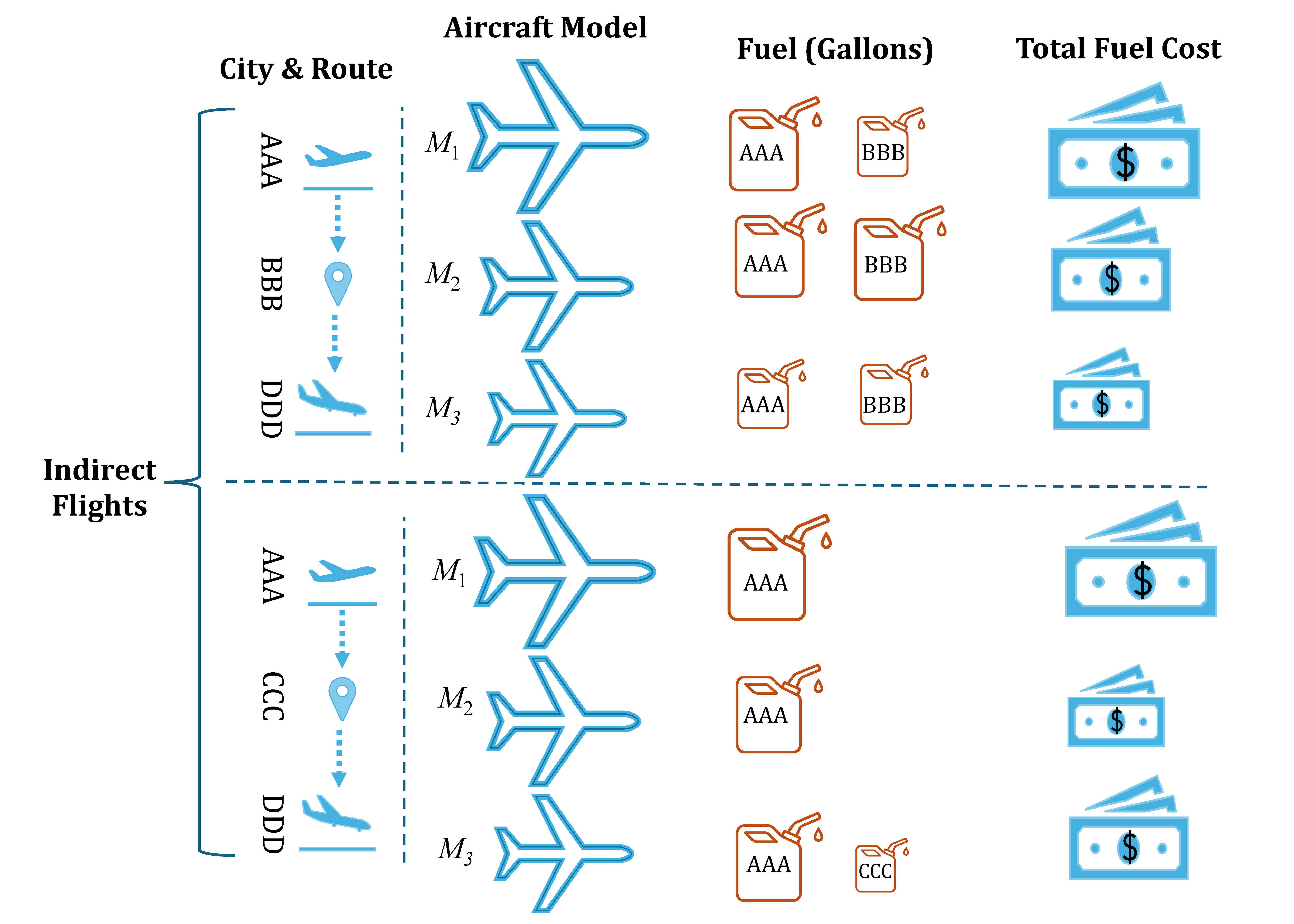
The calculation of fuel costs was based on various factors (Doganis, 2019), such as flight routes, aircraft types, fuel prices, refueling locations, and fuel consumption rates (Calvet, 2024). To show the proposed model, a small-scale case study was introduced. This study assumed a flight departing from city AAA and heading to city DDD, with three possible routes. The routes were grouped into one direct and two indirect routes that included a refueling layover in city BBB or CCC. Table 1 provided the distances for these three routes, measured in miles.
Table 1 The distance from point to point in miles
This study assumed that there were only three models of aircraft available, including C1: Boeing 747-400 (B747), C2: Boeing 777-300ER (B777), and C3: Airbus A330-300 (A330). Each aircraft had distinct fuel consumption rates and performance metrics. Table 2 detailed relevant data for these aircraft, including their maximum takeoff and landing weights (in tons), maximum fuel capacities (in gallons), ranges with maximum payloads (in nautical miles), and normal cruise speeds (in miles per hour).
Table 2 Aircraft models and their specifications
Table 3 presented fuel consumption (Hassan, Sobaih, and Salem, 2021) for each aircraft model across the three flight routes, indicating the minimum fuel consumption for the model on each segment of these routes.
Given the analysis of three flight routes and variations in fuel costs across fueling stations in the departure city (AAA) and the two layover cities (BBB and CCC), informed decisions about flight routes, aircraft types, and refueling locations were crucial. Determining the appropriate amount of fuel for each refueling stop while considering these factors was also essential. A 0-1 MILP model addressing this problem was introduced in the following section.
Table 3 Minimum fuel consumption (in gallons) of each model for each route segment.
The Proposed Mathematical Model
The mathematical model developed for AAA-DDD flight route case study was designed to optimize flight routes, aircraft types, and refueling locations, as well as fuel quantities at each stop, with the aim of minimizing total fuel costs. The model adopted a systematic design covering three key steps, including defining decision variables, formulating the objective function, and establishing constraints. The constraints ensured that the optimal values of the decision variables satisfied all operational and logistical requirements. The process began by identifying decision and auxiliary variables, along with essential input parameters. These components were then integrated to construct the objective function and specify the constraints.
2.2.1. A Set of Notations:
The notations and their representations in the context of the problem were categorized into decision variables, auxiliary variables, and input parameters as follows.
Decision Variables:
Let R1, R2, and R3 denote the flight routes 1,2, and 3, where:
route R1 represented the direct route AAA–DDD,
route R2 was the indirect route AAA–BBB–DDD that refueled at BBB,
route R3 represented the indirect route AAA–CCC–DDD, refueling at CCC.
Ri = 1 when route i was selected and Ri = 0 when route i was not selected, where i = 1, 2, 3.
Let M1, M2 and M3 denoted the aircraft models B747, B777, and A330, respectively.
Mj = 1 when aircraft model j was selected and Mj = 0 when model j was not selected, where j = 1, 2, 3
Let P1, P2, and P3 represented refueling cities AAA, BBB, and CCC, respectively.
Pk = 1 when refueling city k was selected and Pk = 0 if city k was not selected, where k = 1, 2, 3.
Fijk 0 represented the quantity of fuel, in gallons, refueled on the selected route i using aircraft model j at refueling city k, where i,j,k = 1, 2, 3.
Auxiliary Variables:
Hijk = 1 when route i with aircraft model j, and refueling city k was selected.
Hijk = 0 when route i with aircraft model j and refueling city k was not selected,
where i,j,k = 1, 2, 3.
Gij = 1 when route i with aircraft model j was selected.
Gij = 0 when route i with aircraft model j was not selected, where i,j = 1, 2, 3.
Input Parameters
Let denoted fuel costs at refueling cities AAA, BBB, and CCC, respectively.
The auxiliary variables Hijk and Gij were introduced to ensure that fuel consumption rates and aircraft tank capacities were in line with the relevant aircraft specifications.
2.2.2. The Objective Function:
The objective of this model was to minimize the total fuel expenses as shown in the following Equation (1), i.e.,
Minimize
2.2.3. The Constraints:
Equation (2) specified that while three flight routes were available for selection, only one could be selected.
R1 + R2 + R3 = 1 (2)
Equation (3) indicated that, although three aircraft models were available for selection, only one was chosen.
M1 + M2 + M3 = 1 (3)
Equation (4) through (8) defined the constraints related to refueling points, as explained below.
Since AAA was the departure city, all aircraft needed to be fueled at P1.
P1 = 1 (4)
For flight routes with layovers, refueling at the layover cities P2 and P3 was optional.
P1 + P2+ P3 2 (5)
Route R1 was a direct flight route, making refueling only occur at the departure city.
R1 + P2+ P3 1 (6)
Routes R2 and R2 involved layover cities, making it possible to be refueled or not, as specified in equations (7) and (8).
P2 R2 (7)
P3 R3 (8)
For each scenario, which included a selected flight route, aircraft types, and refueling location, the required fuel quantity was determined using auxiliary 0-1 variables (Hijk). The variables ensured that fuel quantity satisfied the minimum fuel consumption required for aircraft types on each segment of the selected route while staying in the maximum fuel tank capacity, as defined in Equations (9) through (38).
R1 + M1 + P1 – 2 3H111
R1 + M1 + P1 (9)
35,854.40H111 F111
45,714.98H111 (10)
R1 + M2 + P1 – 2 3H121
R1 + M2 + P1 (11)
28,890.58H121 F121
38,428.16H121 (12)
R1 + M3 + P1 – 2 3H131
R1 + M3 + P1 (13)
26,612.44H131 F131 ? 20,608.59H131 (14)
R2 + M1 + P1 – 2 3H211 ? R2 + M1 + P1 (15)
24,149.52H211 ? F211 45,714.98H211 (16)
R2 + M1 + P2 – 2 ? 3H212 R2 + M1 + P2 (17)
H212 F212
45,714.98H212 (18)
R2 + M2 + P1 – 2 3H221
R2 + M2 + P1 (19)
19,203.98H221 F221 ? 38,428.16H221 (20)
R2 + M2 + P2 – 2 3H222
R2 + M2 + P2 (21)
H222 F222
38,428.16H222 (22)
R2 + M3 + P1 – 2 3H231
R2 + M3 + P1 (23)
14,229.58H231 F231
20,608.59H231 (24)
R2 + M3 + P2 – 2 3H232
R2 + M3 + P2 (25)
H232 F232
20,608.59H232 (26)
R3 + M1 + P1 – 2 3H311
R3 + M1 + P1 (27)
15,255.85H311 F311
45,714.98H311 (28)
R3 + M1 + P3 – 2 3H313
R3 + M1 + P3 (29)
H313 F313
45,714.98H313 (30)
R3 + M2 + P1 – 2 3H321
R3 + M2 + P1 (31)
12,190.84H321 F321
38,428.16H321 (32)
R3 + M2 + P3 – 2 3H323
R3 + M2 + P3 (33)
H323 F323
38,428.16H323 (34)
R3 + M3 + P1 – 2 3H331
R3 + M3 + P1 (35)
9,023.62H331 F331
20,608.59H331 (36)
R3 + M3 + P3 – 2 3H333
R3 + M3 + P3 (37)
H333 F333
20,608.59H333 (38)
When selecting flight routes R2 and R3, refueling needed to occur both at the departure city and the layover city. The combined fuel quantity, controlled by the auxiliary 0-1 variables (Gij), must equal or exceed the total fuel consumption required for the entire route, as described in Equations (39) through (50).
R2 + M1 – 1 2G21
R2 + M1 (39)
48,140.18G21 F211 + F212 (40)
R2 + M2 – 1 2G22
R2 + M2 (41)
38,282.48 G22 F221 + F222 (42)
R2 + M3 – 1 2G23
R2 + M3 (43)
28,325.56G23 F231 + F232 (44)
R3 + M1 – 1 2G31
R3 + M1 (45)
43,766.38G31 F311 + F313 (46)
R3 + M2 – 1 2G32
R3 + M2 (47)
34,866.62G32 F321 + F323 (48)
R3 + M3 – 1 2G33
R3 + M3 (49)
27,945.59G33 F331 + F333 (50)
For indirect flight routes R2 and R3, the total fuel quantity combined from the departure and layover cities must not surpass fuel tank capacity of the aircraft types being used, as detailed in Equations (51) through (56).
F211 – 24,149.52 + F212 45,714.98 (51)
F221 – 19,203.98 + F222 38,428.16 (52)
F231 – 14,229.58 + F232 20,608.59 (53)
F311 – 15,255.85 + F313 45,714.98 (54)
F321 – 12,190.84 + F323 38,428.16 (55)
F331 – 9,023.62 + F333 20,608.59 (56)
The decision variable (Fijk), representing fuel quantity, was required to always be greater than or equal to 0. Other decision variables, which indicated whether a particular option was selected, must take on values of either 0 or 1, as outlined in Equations (57) and (58).
Fijk 0 (57)
Ri, Mj, Pk, Hijk, Gij = 0 or 1 (58)
Assuming fuel prices at refueling points AAA, BBB, and CCC were set at $1.24, $1.15, and $1.33 per gallon, respectively, a detailed analysis was performed to evaluate eight potential fuel cost scenarios based on the model in the case study. The scenarios accounted for various combinations of flight routes, aircraft types, and refueling locations. The results, which showed fuel quantities to be refueled at the starting point of each route segment for all flight routes and aircraft types, along with their corresponding total fuel costs, were presented in Table 4.
In Scenario 3, where the flight followed an indirect route from AAA to DDD with a layover in BBB, using the B747 aircraft, refueling quantities at AAA and BBB were 24,149.52 gallons and 3,990.66 gallons, respectively. The lowest total fuel cost for this scenario was $57,534.66. Despite Scenarios 6 and 7 being indirect routes with layovers in CCC, the aircraft did not require refueling at CCC, as fuel loaded at AAA was sufficient to complete the entire route.
Table 4 The refueled quantities at the starting point of each route segment for both direct and indirect flights, across various aircraft types, along with their corresponding total fuel costs
The optimal solutions obtained from the proposed model were detailed in Table 5, with the final values of all decision variables. The results showed the decision variables R2, M3, P1, and P2 were assigned a value of 1, indicating that the most cost-effective configuration involved selecting flight route R2: AAA-BBB-DDD, using aircraft types M3: A330-300. According to the optimal plan, the aircraft was first refueled at the departure city (P1: AAA), with a total of F231 = 14,229.58 gallons. It was then refueled at the layover city (P2: BBB), with a total of F232 = 14,095.98 gallons. The configuration results in the lowest possible fuel cost of $33,855.06 was calculated as (14,229.58 gallons x $1.24 per gallon) + (14,095.98 gallons x $1.15 per gallon). The results showed the optimization model's effectiveness in minimizing fuel costs while considering various factors.
When fuel prices at refueling locations differ from the fixed values assumed in this study, the optimal solution might change accordingly. This could affect the selection of flight routes, aircraft types, refueling locations, and fuel quantities. However, the proposed model remained adaptable and robust, capable of handling varying price conditions and scaling up for larger or more complex problems without compromising effectiveness.
Table 5 Final values of the decision variables
In conclusion, this study talked about a 0-1 MILP model that was used to lower the fuel costs for flight with passengers. The model looked at important factors, like which flight routes to take, what kinds of planes to use, fuel prices at refueling spots, and how much fuel was used. The 0-1 MILP had a setup that helped to compare different options, making the cheapest way to be picked. The model chose the best flight route, checked if refueling was needed, and decided where it would be best to refuel. Also, the 0-1 MILP figured out exactly how much fuel would be needed at every stop, making sure the plane could finish its trip without carrying too much fuel or spending extra money. This model helped save money and made operations better. One limitation of the study was the assumption of fixed fuel costs at refueling locations. However, the act of being flexible allowed the designed model to be updated with new price inputs, maintaining its relevance even under fluctuating market conditions. A 0-1 MILP could also be scaled and adapted to address real-world and large-scale problems by adjusting specific constraints. The flexibility made it a valuable tool for flight planning, enabling detailed analysis and comparison of fuel costs across different flight routes, aircraft types, and refueling points, ultimately contributing to lower operational costs. The proposed model offered significant environmental benefits. By optimizing fuel consumption and refueling strategies, it helped reduce fuel burn and lower carbon emissions. Identifying more fuel-efficient routes and minimizing unnecessary refueling contributed to decreasing the environmental impact of air travel. Furthermore, the model could be adjusted to prioritize greener aircraft models or alternative fuels, promoting sustainability in aviation. This mathematical model was in line with cost efficiency with environmental objectives, reducing both operational costs and emissions.
| Filename | Description |
|---|---|
| R1-IE-7285-20241021085906.docx | --- |
Alba, E., Blum, C., Asasi, P., Leon, C., Gomez, J.A., 2009. Optimization Techniques For Solving Complex Problems. Hoboken, New Jersey, USA: John Wiley & Sons, Inc
Alonso-Ayuso, A., Escudero, L.F., Olaso, P., Pizarro, C., 2013. Conflict Avoidance: 0-1 Linear Models For Conflict Detection & Resolution. TOP (Transactions in Operations Research), Volume 21, pp. 485–504 DOI: 10.1007/s11750-011-0224-6
Ardi, R., Nurkamila, S., Citraningrum, D.L., Zahari, N.T., 2023. Reverse Logistics Network Design For Plastic Waste Management In Jakarta: Robust Optimization Method. International Journal of Technology, Volume 14(7), pp. 1560–1569: https://doi.org/10.14716/
ijtech.v14i7.6681
Aydo?an, E., Cetek, C., 2022. Aircraft Route Optimization With Simulated Annealing For a Mixed Airspace Composed of Free and Fixed Route Structures. Aircraft Engineering and Aerospace Technology, Volume 95(2), pp. 637–648 DOI: 10.1108/AEAT-11-2021-0343
Bijlsma, S.J., 2009. Optimal Aircraft Routing in General Wind Fields. Journal of Guidance Control and Dynamics, Volume 32(3), pp. 1025–1029 DOI: 10.2514/1.42425
Calvet, L., 2024. Towards Environmentally Sustainable Aviation: A Review on Operational Optimization. Future Transportation, Volume 4(2), pp. 518–547 https://doi.org/10.3390/futuretransp4020025
Cobbs, R., Wolf, A., 2004. Jet Fuel Hedging Strategies: Options Available for Airlines and a Survey of Industry Practices. Available Online at http://www. kellogg. northwestern. edu/research/fimrc/papers/jet fuel. pdf , Accessed on October 17, 2024
Doganis, R., 2019. Flying off Course. s.l.:Routledge, Taylor & Francis Group, Boca Raton, Florida,USA
Doulgeris, G., Kirner, R., Laskaridis, P., 2011. The Effect of Refueling Stop On Long Haul Air Transport Greenhouse Emissions. Journal of Environment and Engineering, Volume 6(3), pp. 579–594 DOI: 10.1299/jee.6.579
Elzayady, N., Elghandour, E., 2021. Design Optimization to Improve the Performance of the Aircraft Composite Structures. Journal of Mechanical Science and Technology, Volume 35, pp. 4381–4388 DOI 10.1007/s12206-021-0909-1
Gayle, P.G., Lin, Y., 2020. Cost Pass-Through In Commercial Aviation: Theory and Evidence. Economic Inquiry, Volume 59(2), pp. 803–828 https://doi.org/10.1111/ecin.12949
Hahn, A., 2012. Staging Airliner Service. Belfast, Northern Ireland
Hassan, T.H., Sobaih, A.E.E., Salem, A.E., 2021. Factors Affecting the Rate of Fuel Consumption in Aircrafts. Sustainability, Volume 13(14), p. 8066 https://doi.org/10.3390/su13148066
Hillier, F.S., Lieberman, G.J., 2015. Introduction to Operations Research. s.l.:McGraw-Hill, New York, NY
Hsu, C.-I., Eie, W.-Y., 2013. Airline Network Design and Adjustment in Response to Fluctuation in Jet Fuel Prices.” Mathematical and Computer Modelling, Volume 58, pp. 1791–1803 https://doi.org/10.1016/j.mcm.2013.04.005
Hubert, T., Guo, C., Mouton, C.A., Powers, J.D., 2015. Tankering Fuel on U.S. Air Force Transport Aircraft, Santa Monica, CA: RAND Corporation
Kannon, T.E., Nurre, S.G., Lunday, B.J., Hill, R.R., 2014. The Aircraft Routing with Air Refueling Problem: Exact And Greedy Approaches. Montréal, Canada, s.n., pp. 1–8
Kheraie, A.Z., Mahmassani, H.S., 2012. Leveraging Fuel Cost Differences in Aircraft Routing by Considering Fuel Ferrying Strategies. Transportation Research Record, Volume 2300, pp. 139–146 https://doi.org/10.3141/2300-16
Kondili, E., 2005. Review of Optimization Models in the Pollution Prevention and Control. Computer Aided Chemical Engineering, pp. 1627–1632, pp. 1627–1632 https://doi.org/10.1016/S1570-7946(05)80113-0
Kusumalestari, A.S., Suryanegara, M., Sudibyo, H., Soekirno, S., Ruseno, N., 2024. Proposing Method for Airframe Noise Prediction Benefitting Indonesian Aircraft Design. International Journal of Technology, Volume 15(5), pp. 1582–1592 DOI : https://doi.org/10.14716/ijtech.v15i5.7094
Matousek, J., Gärtner, B., 2007. Understanding and Using Linear Programming. USA: Springer Science & Business Media
McCarty, L.A., Cohn, A.M., 2018. Preemptive Rerouting of Airline Passengers Under Uncertain Delays. Computers & Operations Research, Volume 90, pp. 1–11 https://doi.org/10.1016/j.cor.2017.09.001
Nahry, Tjahjono, T., Brotoadi, T., 2015. The Application of Optimization Model of Off-Street Parking Management with Dynamic Simulation. International Journal of Technology, Volume 6(2), pp. 236–243 https://doi.org/10.14716/ijtech.v6i2.974
Office of Industrial Economics, 2021. Full Report: Aviation and Logistics Industry, Bangkok: Office of Industrial Economics.
Oguntona, O., Cui, A., Plötner, K.O.,Hornung, M., 2016. Fleet Development Planning of Airlines: Incorporating the Aircraft Operating Economics Factor. In: 30th ICAS Congress Daejeon, Korea, s.n., pp. 1–9
Park, Y., O'Kelly, M.E., 2018. Examination of Cost-Efficient Aircraft Fleets Using Empirical Operation Data In US Aviation Markets. Journal of Air Transport Management, Volume 69, pp. 224–234 https://doi.org/10.1016/j.jairtraman.2017.02.002
Piu, F., Speranza, M.G., 2014. The Locomotive Assignment Problem: A Survey on Optimization Models. International Transactions in Operational Research, Volume 21, pp. 327–352 https://doi.org/10.1111/itor.12062
Qiu, L., Wang, J., Qian, F., 2023. Research on Performance Parameter Optimization for Aircraft Based on Fuel Cost Objectives. In: International Conference on Power, Communication, Computing and Networking Technologies
Rosyidi, C.N., Fatmawati, A., Jauhari, W.A., 2016. An Integrated Optimization Model for Product Design And Production Allocation in a Make to Order Manufacturing System. International Journal of Technology, Volume 7(5), pp. 819–830 DOI: https://doi.org/10.14716/ijtech.v7i5.1173
Singh, V., Sharma, S.K., 2015. Fuel Consumption Optimization in Air Transport: A Review, Classification, Critique, Simple Meta-Analysis, and Future Research Implications. European Transport Research Review, Volume 7, pp. 1–24 https://doi.org/10.1007/s12544-015-0160-x
Sioshansi, R., Conejo, A.J., 2017. Mixed-Integer Linear Optimization. In: Optimization in Engineering, Springer Optimization and Its Applications. Springer International Publishing AG, Cham, Switzerland
Smirti, M., Hansen, M., 2009. Assessing the Role of Operating, Passenger, and Infrastructure Costs In Fleet Planning Under Fuel Price Uncertainty. University of California Transportation Center, Volume 881, pp. 1–15
Swidan, H., Merkert, R., Kwon, O.K., 2019. Designing Optimal Jet Fuel Hedging Strategies for Airlines – Why Hedging Will Not Always Reduce Risk Exposure. Transportation Research Part A: Policy and Practice, Volume 130, pp. 20–36 https://doi.org/10.1016/j.tra.2019.09.014
Wensveen, J.G., 2015. Air Transportation, a Management Perspective. s.l.:Ashgate Publishing Limited, Farnham United Kingdom
Widodo, E., Putra, F.S.U., Hartanto, D., Arvitrida, N.I., Bagastyo, A.Y., Warmadewanthi, I., Soehartanto, T., 2023. Analysis of Bittern Recovery Facility using Mixed-Integer Nonlinear Programming: Centralized, Decentralized, and Hybrid Scenarios. International Journal of Technology, Volume 14(3), pp. 638–648 DOI : https://doi.org/10.14716/ijtech.v14i3.5437
Wongwiwat, P., 2014. Pre-flight Planning. EAU Heritage Journal Science and Technology, Volume 8(1), pp. 1–9
Xu, J., Ning, A., Bower, G., Kroo, I., 2014. Aircraft Route Optimization for Formation Flight. Journal of Aircraft, Volume 51(2), pp. 490–501 https://doi.org/10.2514/1.C032154
Xu, J., Ning, S., Bower, G., Kroo, I., 2012. Aircraft Route Optimization for Heterogeneous Formation Flight. Honolulu, HI, s.n
Zhang, D., Klabjan, D., 2017. Optimization for Gate Re-assignment. Transportation Research Part B-methodological, Volume 95, pp. 260–284 https://doi.org/10.1016/j.trb.2016.11.006
