Process of Solving Multi-Response Optimization Problems Using a Novel Data Envelopment Analysis Variant-Taguchi Method
Corresponding email: wanrop.kh@ksu.ac.th
Published at : 24 Dec 2024
Volume : IJtech
Vol 15, No 6 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i6.7134
Wichapa, N., Pawaree , N., Nasawat, P., Chourwong, P., Sriburum, A., Khanthirat, W., 2024. Process of Solving Multi-Response Optimization Problems Using a Novel Data Envelopment Analysis Variant-Taguchi Method. International Journal of Technology. Volume 15(6), pp. 2038-2059
| Narong Wichapa | Department of Industrial Engineering, Faculty of Engineering and Industrial Technology, Kalasin University, Kalasin, 46000, Thailand |
| Narathip Pawaree | Department of Industrial Management, Faculty of Technology, Udon Thani Rajabhat University, Udon Thani, 41000, Thailand |
| Pariwat Nasawat | Department of Logistics and Process Engineering, Faculty of Industrial Technology, Rajabhat Rajanagarindra University, 24000, Thailand |
| Prawach Chourwong | Department of Logistics and Process Engineering, Faculty of Industrial Technology, Rajabhat Rajanagarindra University, 24000, Thailand |
| Anucha Sriburum | Department of Industrial Engineering, Faculty of Engineering and Industrial Technology, Kalasin University, Kalasin, 46000, Thailand |
| Wanrop Khanthirat | Department of Industrial Engineering, Faculty of Engineering and Industrial Technology, Kalasin University, Kalasin, 46000, Thailand |
Multi-response
optimization (MRO) is important to modern manufacturing that requires
simultaneous consideration of multiple performance metrics to achieve high
efficiency and quality. Therefore, this study presents an innovative hybrid
method that combines the Data Envelopment Analysis Variant (DEAV) model with
Taguchi to address the challenges associated with MRO. The DEAV model improves
traditional DEA by incorporating multiple attribute decision-making (MADM)
principles to offer a comprehensive evaluation framework. Taguchi uses
efficiency scores from the DEAV model to enable optimal parameter determination
through Taguchi optimization. Moreover, the hybrid method was validated using
two examples, including optimization of a fish scale scraping machine and the
CNC turning process of ST37 steel. The results showed that the DEAV-Taguchi
method produced more efficient and reliable outcomes than existing methods,
significantly improving key performance metrics such as surface roughness and
material removal rate. The main contribution of this study was the development
of a robust optimization framework that balanced multiple conflicting
objectives in manufacturing processes. Future studies are expected to apply the
method to different materials and processes, expand experimental designs, and
assess the economic and environmental impacts of optimized parameters. The
DEAV-Taguchi method also offers a significant advancement in MRO, providing a
versatile and effective solution for modern manufacturing optimization.
CNC turning optimization; Data envelopment analysis variant; Multi-response optimization; Manufacturing processes; Taguchi method
Multi-response optimization (MRO) is very important in contemporary manufacturing processes due to the usefulness in simultaneous consideration of multiple performance metrics to achieve both efficiency and high quality. However, conventional optimization methods have frequently failed to adequately address the complexities associated with balancing multiple conflicting objectives. This is despite the need to optimize manufacturing processes, specifically in high-precision environments, in order to enhance product quality, reduce costs, and increase efficiency (Soori, Arezoo, and Dastres, 2023; Abdelaoui, Jabri, and Barkany, 2023; Sulaiman et al., 2022; Yang et al., 2019). Therefore, there is a need to develop new, promising, and efficient methods to address MRO challenges in order to ensure the effective management of the issues identified. The introduction of innovative strategies for MRO can lead to better handling of the complexities and conflicting objectives inherent in modern manufacturing processes which are required to improve efficiency and quality.
Design of Experiments (DOE) is
a systematic method developed in the early 20th century by Sir
Ronald Fisher to study the relationships between factors affecting process and
output. The method is considered important for improving process efficiency and
product quality by enabling structured experimentation and analysis of different
factors. An example is the method introduced by Genichi Taguchi which is
considered robust and emphasizes improving quality through design rather than
inspection. It uses orthogonal arrays to study a large number of variables with
a minimal number of experiments, leading to reduced costs and time (Taguchi, 1986). The focus of the method on
minimizing variability through the use of signal-to-noise (S/N) ratios also
ensures specific effectiveness in optimizing manufacturing processes.
Furthermore, its ability to optimize parameters with fewer experimental runs compared
to traditional methods leads to cost-effectiveness and efficiency (Kantasiri et al., 2024; Chen et al., 2024;
Lestari et al., 2024; Sulaiman et al., 2022).
Multi-Attribute Decision Making
(MADM) methods which are an example of Multi-Criteria Decision Making (MCDM)
have been integrated into DOE to tackle complex optimization problems related
to multiple conflicting objectives or responses. For example, Grey Relational
Analysis (GRA), the Technique for Order of Preference by Similarity to Ideal
Solution (TOPSIS), Data Envelopment Analysis Ranking (DEAR), and Complex
Proportional Assessment (COPRAS) have also been effectively used to solve MRO
problems (Shivakumar and Panchangam, 2024; Kumar et
al., 2024; Pawaree, Phokha, and
Phukapak, 2024; Kannan et al., 2023; Sriburum, Wichapa, and Khanthirat,
2023; Liu et al., 2023; Yang et al., 2023; To-on, Wichapa, and
Khanthirat, 2023; Kamath et al., 2022; Yaser and Shunmugesh, 2019;
Vellaiyan, Amirthagadeswaran, and Sivasamy, 2018;
Zavadskas, Turskis, and Kildien?, 2014;
Liao and Chen, 2002). These MADM methods facilitate the evaluation and
prioritization of multiple alternatives based on a set of criteria, aiding
process of making more informed decisions. Moreover, the combination of MADM
with DOE has led to the provision of a more robust optimization solution that
balances multiple performance metrics and subsequently enhances overall
manufacturing efficiency.
The integration of Taguchi
method into MADM has proven effective in solving MRO problems. For example, (Kumar, Kumar, and Rajkumar, 2022) combined
Taguchi and GRA to optimize CNC end-milling parameters for AISI H11 tool steel,
achieving optimal surface roughness and MRR. A research by (Zhujani et al., 2024) also applied
Taguchi-based DOE method combined with GRA and Analysis of Variance (ANOVA) to
determine the optimal machining parameters for turning Inconel 718, a
high-strength nickel-based superalloy widely used in the aerospace industry.
Moreover, a research by (Sristi, Zaman, and Dhar, 2022)
conducted a comparative study of different hybrid Taguchi-based MADM methods
for optimizing hard-turning parameters. The study utilized COPRAS, TOPSIS, and
GRA to optimize parameters such as cooling environment, cutting speed, and feed
rate. The optimal process parameters obtained from all three methods were
consistent, showing the effectiveness of these methods in improving
machinability and process performance. A research by (Sriburum,
Wichapa, and Khanthirat, 2023) also utilized a novel TOPSIS linear
programming (modified TOPSIS) model based on Taguchi method for solving MRO
problems in the fish scale scraping machine. The study reported improvements in
fish scaling removal efficiency and reduction in fish damage, emphasizing the
utility of combining the modified TOPSIS with Taguchi for optimizing complex
processes.
Kamath et al., (2022)
evaluated the effect of process parameters on the face milling machining
process during process of machining Al/TiB2 metal matrix composite. This was
achieved using Taguchi-DEAR method to evaluate performance metrics, including
MRR and surface roughness. A research by (Moganapriya
and Rajasekar, 2023) also explored the use of titanium aluminum
nitride/tungsten carbide-coated inserted in dry turning, optimizing machining
variables to improve flank wear, MRR, and surface roughness using a
DEAR-Taguchi method. The application of Taguchi L16 design and ANOVA showed the
significant influence of feed per tooth on the outcomes. Moreover, the
combination of GRA and DEAR with Taguchi method produced an optimal cutting
regime that enhanced surface roughness and material removal rate, with feed per
tooth having the most substantial impact on performance metrics. Several MADM
methods have successfully addressed MRO problems, but each method has
advantages and disadvantages. A critical drawback identified in almost all was
related to data normalization which could adversely affect the reliability of
the results. The computational complexity of MADM methods could also increase
significantly when processing large datasets. Therefore, new MADM methods
needed to be developed in order to overcome these primary limitations.
The Data Envelopment Analysis
(DEA) model developed by (Charnes, Cooper, and
Rhodes, 1978) can evaluate the relative efficiency of decision-making
units (DMUs). This efficiency is often calculated as the ratio of the weighted
sum of outputs to the weighted sum of inputs. Moreover, the linear programming
model, called the CCR, has the ability to determine the optimal weights for
each DMU in order to ensure none of the efficiency scores exceeds one. DEA
offers several advantages and the most important is the ability to measure
efficiency without requiring data normalization, thereby simplifying the
preprocessing step. As a linear programming model, DEA can be solved using
different solvers, making the process computationally efficient. It provides a
comprehensive measure of efficiency by comparing multiple inputs and outputs
across DMUs without needing a predefined functional form (Fan et al., 2017, Wang,
Nguyen, and Wang, 2016). However, the traditional DEA model,
specifically the CCR, is not suitable for addressing MADM problems due to the
inability to distinguish among efficient units (Li et
al., 2022; Shi et al., 2021; Shi, Wang, and Zhang, 2019; Li et al.,
2018). The model provides an efficiency score of one to all DMUs on the
efficient frontier, leading to the classification of multiple units as equally
efficient. This lack of discrimination hinders the establishment of a clear
ranking order among efficient units, causing some challenges in the process of
ranking all DMUs precisely. A promising method is to integrate the concepts of
DEA into MADM in order to overcome this limitation and develop an effective
tool for solving MRO problems in the context.
The concept inspired the
conduct of this study to present an innovative method that combined the
principles of DEA and MADM towards producing the novel Data Envelopment
Analysis Variant (DEAV) specifically designed for MRO problems. The DEAV model
combined with Taguchi method was proposed and evaluated using two numerical
examples in order to deliver a robust solution for MRO challenges. This
advanced method aimed to offer a comprehensive framework for MRO. Therefore,
the contributions of this study are stated as follows:
1) The introduction of the
DEAV model produced through the inclusion of MADM principles as an enhancement
to the traditional DEA. The model provided weights to each criterion through
decision-makers or established methods such as Analytic Hierarchy Process
(AHP), Best-Worst Method (BWM), Criteria Importance Through Inter-criteria
Correlation (CRITIC), and Entropy to provide a flexible and adaptable
framework.
2) The combination of the
DEAV model with Taguchi method as a comprehensive optimization framework to
effectively balance multiple conflicting objectives. The Taguchi method
utilizes efficiency scores from the DEAV model to obtain optimal parameters
through optimization process.
3) The method was
subsequently validated through two examples, including optimization of a fish
scale scraping machine and the CNC turning process of ST37 steel. The DEAV-
Taguchi method showed significant improvements in
key performance metrics such as surface roughness and material removal rate,
outperforming existing methods.
4) The method was confirmed
to be adaptable for other MRO or MADM problems, showing versatility across
different industrial settings. It was suggested that future studies should
apply the method to different materials and processes, expand experimental designs,
and assess economic and environmental impacts.
The remainder of this study is organized as
follows: Section 2 focuses on the methodology designed to determine the optimal
machining parameters. Section 3 presents the results which show the
effectiveness of the proposed method. Lastly, Section 4 provides a summary of
the key results with an emphasis on the practical implications for
manufacturing optimization and the potential of the method to address MRO
problems.
Figure 1 The proposed framework of the study
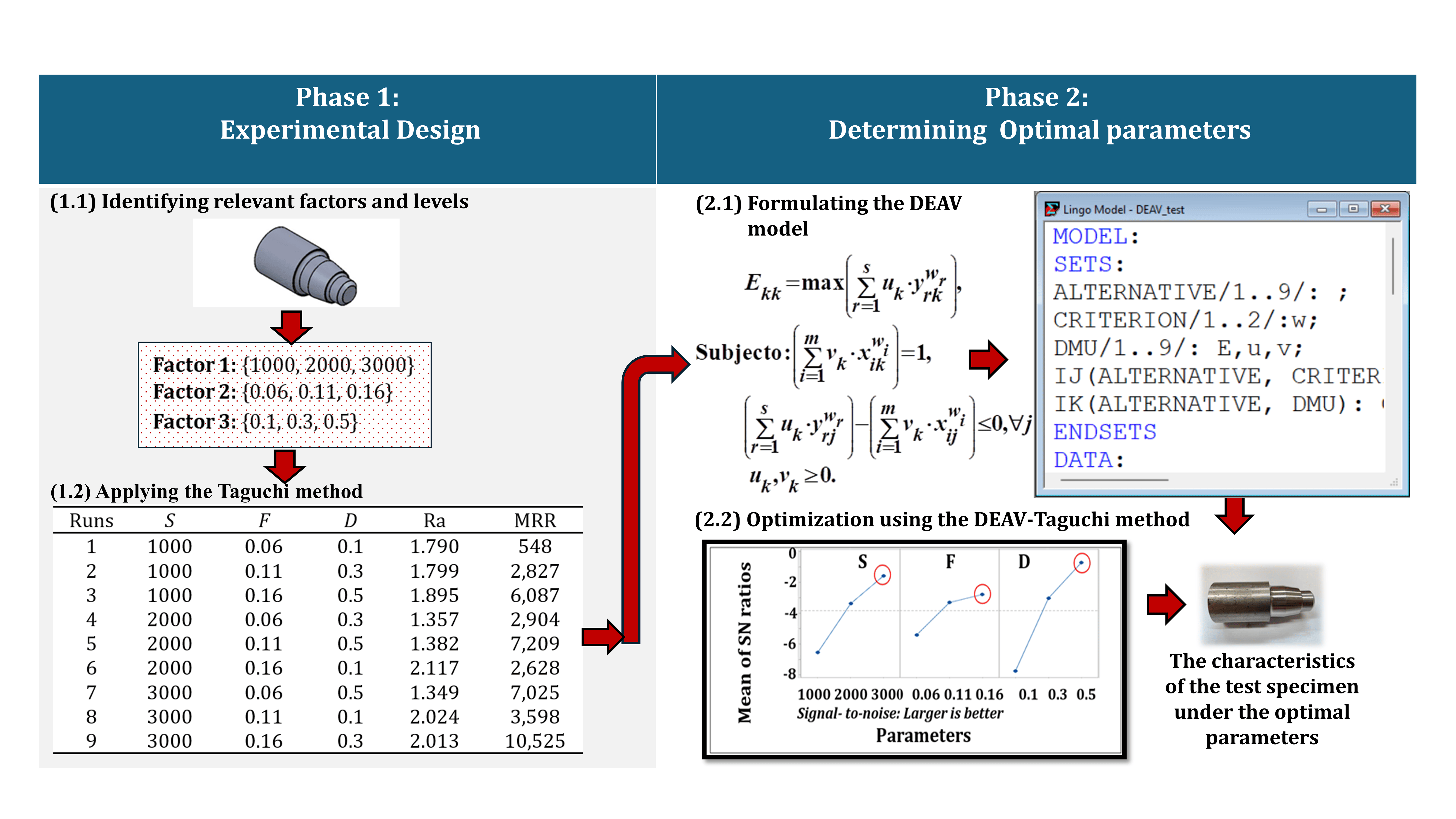
2.1. Phase1: Experimental design
The
experimental design used in this study was further divided into the following
two sub-steps.
2.1.1. Identifying
the relevant factors and subsequent levels
The sub-step focused on
determining the critical variables influencing the outcome of process and
specifying different values, conditions, or levels. This was important to
design the experiments that precisely captured the effects of each factor on
response variables.
2.1.2. Applying Taguchi method
The sub-step focused on
implementing a systematic method to efficiently plan the experiments with the
aim of identifying the optimal conditions. The method emphasized the reduction
of variability and enhancement of quality through the application of orthogonal
arrays to examine a large number of variables with a minimal number of
experiments.
2.2. Phase 2: Determining the optimal parameters
Process
of determining the optimal parameters was also divided into the following two
sub-steps.
2.2.1. Formulating
a DEAV model
The DEAV model was used to convert responses obtained into a single output. The concepts of the original DEA model required evaluating the efficiency score for each run according to the criterion. In the decision matrix, each set of runs was treated as a set of DMUs, and responses were categorized as inputs and outputs. Moreover, the efficiency of DMUs was assessed by comparing the inputs and outputs to a frontier. This was achieved by using linear programming to calculate efficiency scores and identify optimal DMUs and inefficiencies. The aim was to determine the optimal weights that maximize the efficiency score (Ekk) for each DMU. A score of 1 shows efficiency while values below 1 suggest an improvement in DMU by reducing inputs or increasing outputs. The DEAV model incorporated MADM concepts and required weights for each criterion which were determined by decision-makers or through methods such as AHP, BWM, CRITIC, and Entropy. The definitions of indices, parameters, objective functions, and constraints are provided in the following sections.
Consider a set of DMUs, denoted as DMUj, each characterized by a set of inputs xij for i = 1,…, m and a set of outputs yri for r =1,…,s. Let uk? represent the weights assigned to the output k evaluated while vk? is the weights assigned to the input k evaluated. The DEAV model is an advanced method for evaluating the performance of DMUs by incorporating multiple inputs and outputs. Therefore, this study focuses on transforming the non-linear DEAV into a linear programming model to enhance computational efficiency and applicability. The novel linear programming model for DEAV was formulated through a series of steps. Initially, the non-linear form was expressed through Equation (1).
The linear programming DEAV model applied
a sophisticated method to assess the performance of DMUs, using both inputs and
outputs to provide a comprehensive evaluation of the efficiency. The aim was to
maximize the efficiency score Ekk, which was the weighted sum
of the variables uk, wr, and yrk.
The model can be applied to a variety of MADM problems due to the ability to
continuously assign importance weights to criteria, which is fundamental to
MADM. Sensitivity analysis was subsequently used to determine the criteria
weights for both inputs and outputs (wr and wi)
in the DEAV model.
2.2.2. Determining
the optimal parameters using a novel DEAV - Taguchi method
This step discusses the
development of Taguchi method from the results obtained from the DEAV model to
optimize the parameters of the proposed machines. The aim was to provide a
detailed and structured method to enhance the performance of machines. At the
initial stage, the efficiency scores for each experimental run were calculated
using the DEAV model to serve as the basis for further analysis. Subsequently,
Taguchi method was applied using Minitab statistical software to provide a
robust analysis of the experimental data. The primary response parameters
considered were two types, including "Larger is better" and
"Smaller is better" which were analyzed using signal-to-noise (S/N)
ratios and considered important in Taguchi method for identifying optimal
settings. Specifically, the factor for "Smaller is better" was
calculated through Equation (3) while the factor for "Larger is
better" was determined according to Equation (4).
Where, y
represents response, and n denotes the number of replications. Moreover,
the Ekk response derived from the proposed DEAV model was
calculated based on the objective that larger values were preferable as shown
in Equation (4).
Figure 2 The step-by-step process of using the DEAV -Taguchi method
The validity of the proposed method was evaluated using two numerical examples. The first example was the fish scale scraping machine problem investigated by (Sriburum, Wichapa, and Khanthirat, 2023) while the second was a case study of the CNC turning process of ST37 steel. The detailed calculation steps for the examples are provided in Sections 3.1 and 3.2, respectively.
3.1. The fish scale scraping machine problem
The fish scale scraping machine problem investigated by (Sriburum, Wichapa, and Khanthirat, 2023) addressed the MRO challenge, with a particular emphasis on enhancing efficiency while minimizing damage to the fish. Based on the principles of the DEAV model in Equation (2), the efficiency was regarded as the output (y1) while the resulting fish damage was considered the input (x1). Table 1 presents the dataset for this study with a focus on the nine DMUs or runs and each is defined by three factors, including speed (S: rpm), time (T: seconds), and capacity (C: kg) assessed at three different levels.
Table 1 The dataset for the MRO problem of a fish scale scraping machine
Experiment | Speed (rpm) | Time (seconds) | Capacity (kg) | x1 | y1 | Ekk |
1 | 50 | 180 | 20 | 1.200 | 3.800 | 0.9704 |
2 | 50 | 240 | 25 | 1.467 | 4.400 | 0.9444 |
3 | 50 | 300 | 30 | 2.000 | 3.800 | 0.7517 |
4 | 60 | 180 | 25 | 1.467 | 4.933 | 1.0000 |
5 | 60 | 240 | 30 | 1.733 | 4.733 | 0.9012 |
6 | 60 | 300 | 20 | 3.000 | 3.800 | 0.6137 |
7 | 70 | 180 | 30 | 1.533 | 4.533 | 0.9377 |
8 | 70 | 240 | 20 | 3.000 | 3.933 | 0.6244 |
9 | 70 | 300 | 25 | 3.800 | 4.000 | 0.5595 |
The linear programming model could be solved using different optimization software. However, Lingo software was used in this study to determine all the efficiency scores (Ekk) for the fish scale scraping machine problem, as presented in Table 2.
Table 2 The details of the Lingo code for the fish scale scraping machine problem
Lingo code for the DEAV model |
MODEL: SETS: ALTERNATIVE/1..9/: ; CRITERION/1..2/:w; DMU/1..9/: E,u,v; IJ(ALTERNATIVE, CRITERION): X; ENDSETS DATA: X= 1.200 3.800 1.467 4.400 2.000 3.800 1.467 4.933 1.733 4.733 3.000 3.800 1.533 4.533 3.000 3.933 3.800 4.000; N_inputs=1;
w= 0.50, 0.50; !w={wi,wr);
ENDDATA MAX = @SUM(DMU (K): E(K)); @FOR(DMU(K):E(K) = @SUM(CRITERION(J)|j#GT# N_inputs :u(K)*(X(K,J)^w(J) )) ); !Constraints; @FOR(DMU(K): @SUM(CRITERION(J)|J#LE#N_inputs :v(K)*(X(K, J)^w(J) )) = 1 ); @FOR(DMU(K): @FOR(ALTERNATIVE(I): @SUM(CRITERION(J)|j#GT#N_inputs :u(K)*(X(I, J)^w(J) )) <= @SUM(CRITERION(J)|J#LE# N_inputs :@SUM(CRITERION(J):v(K)*(X(I, J)^w(J))) ))); @FOR(DMU(K): u(K)>=0); END |
The Lingo code solved was used to present the Ekk values in the final column of Table 1. This was followed by the application of Minitab statistical software to derive the optimal parameters, leading to the S/N Ratios of the Ekk response listed in Table 3.
Table 3 Response table for S/N Ratios of the Ekk response for the fish scale scraping machine problem
Experiment | Speed (rpm) | Time (seconds) | Capacity (kg) |
1 | -1.0790 | -0.2732 | -2.8642 |
2 | -1.7148 | -1.8304 | -1.8470 |
3 | -3.2312 | -3.9213 | -1.3138 |
Delta | 2.1522 | 3.6481 | 1.5504 |
Rank | 2 | 1 | 3 |
The higher delta value presented in the table shows that process parameters have a more significant impact on the multi-response performance indicator. Consequently, the delta statistics showed that the Ekk response was most influenced by the time (T) followed by speed (S), and then capacity (C). It is important to state that the main effects plot for S/N ratios are shown in Figure 3. The method ensured the selected parameters achieved the maximum desired outcomes, offering a robust framework for optimizing the fish scale scraping machine.
Figure 3 The main effects plot for S/N ratios of the Ekk for the fish scale scraping machine
Figure 3 shows that the optimal parameters to achieve the desired Ekk are a speed of 50 rpm, a time of 180 seconds, and a capacity of 30 kg. Moreover, the ANOVA results for the Ekk response are presented in the following Table 4.
Table 4 ANOVA for S/N ratios for Ekk response for the fish scale scraping machine
Source | DF | Seq SS | Adj SS | Adj MS | F | P |
Speed | 2 | 7.3354 | 7.3354 | 3.6677 | 25.55 | 0.038 |
Time | 2 | 20.1053 | 20.1053 | 10.0527 | 70.03 | 0.014 |
Capacity | 2 | 3.7228 | 3.7228 | 1.8614 | 12.97 | 0.072 |
Residual Error | 2 | 0.2871 | 0.2871 | 0.1435 |
|
|
Total | 8 | 31.4506 |
|
|
|
|
Source | DF | Seq SS | Adj SS | Adj MS | F | P |
The efficiency scores Ekk for each run, derived from the DEAV model calculations, were subjected to ANOVA. The analysis showed that the factors of speed (S), time (T), and capacity (C) significantly influenced the Ekk response at P-values less than 0.05, showing strong statistical significance. Moreover, a detailed comparison of the proposed method with other MADMs such as TOPSIS-LP (Sriburum, Wichapa, and Khanthirat, 2023), TOPSIS (Hwang et al., 1981), WASPAS (Zavadskas et al., 2012), and ARAS (Zavadskas and Turskis, 2010), COPRAS (Zavadskas, Kaklauskas, and Šarka, 1994), and MOORA with the full multiplicative form (Brauers and Zavadskas, 2010) is presented in Table 5.
Table 5 ANOVA for S/N ratios for Ekk response for the fish scale scraping machine
Methods | Original parameters | Optimal parameters |
Proposed | S2: F1: D2 | S1: F1: D3 |
TOPSIS-LP | S2: F1: D2 | S1: F1: D3 |
TOPSIS | S2: F1: D2 | S1: F1: D3 |
WASPAS | S2: F1: D2 | S1: F1: D3 |
ARAS | S1: F1: D1 | S1: F1: D3 |
COPRAS | S1: F1: D1 | S1: F1: D3 |
MOORA | S2: F1: D2 | S1: F1: D3 |
The comparison showed that the optimal parameters identified were consistent (S1:F1:D3) across the majority of MADM methods. The consistency confirmed the robustness and reliability of these methods in optimizing the parameters for the fish scale scraping machine. Moreover, the ranking alternatives of the DEAV model were evaluated against different MADM methods using the original parameters, specifically the decision matrix from Table 1, with weights wR1= 0.50 and wR2 = 0.50 in Table 6 and Figure 4.
Table 6 The ranking comparison of the proposed DEAV model against established MADM methods
Run | DEAV | Rank | TOPSIS | Rank | WASPAS | Rank | ARAS | Rank | TOPSIS | Rank | WASPAS | Rank |
1 | 0.9704 | 2 | 0.8088 | 4 | 0.8814 | 2 | 0.8351 | 1 | 1.0000 | 1 | 1.9263 | 2 |
2 | 0.9444 | 3 | 0.8568 | 2 | 0.8546 | 3 | 0.7204 | 3 | 0.8528 | 3 | 1.8245 | 3 |
3 | 0.7517 | 6 | 0.6408 | 6 | 0.6825 | 6 | 0.4547 | 6 | 0.5351 | 6 | 1.1558 | 6 |
4 | 1.0000 | 1 | 0.9004 | 1 | 0.9067 | 1 | 0.8033 | 2 | 0.9471 | 2 | 2.0455 | 1 |
5 | 0.9012 | 5 | 0.7964 | 5 | 0.8205 | 5 | 0.6584 | 5 | 0.7727 | 5 | 1.6613 | 5 |
6 | 0.6137 | 8 | 0.2961 | 8 | 0.5701 | 8 | 0.3358 | 8 | 0.3898 | 8 | 0.7705 | 8 |
7 | 0.9377 | 4 | 0.8527 | 3 | 0.8495 | 4 | 0.7067 | 4 | 0.8344 | 4 | 1.7987 | 4 |
8 | 0.6244 | 7 | 0.2994 | 7 | 0.5817 | 7 | 0.3530 | 7 | 0.4093 | 7 | 0.7975 | 7 |
9 | 0.5595 | 9 | 0.0394 | 9 | 0.5347 | 9 | 0.3260 | 9 | 0.3756 | 9 | 0.6403 | 9 |
Figure 5 The Spearman correlation coefficients for the fish scale scraping machine problem
Figure 5 shows the Spearman correlation coefficients for the comparison between the DEAV model and other well-known MADM methods. The results provided a strong correlation in ranking alternatives between the DEAV model and other MADM methods. These were specifically observed through the 0.950 recorded with TOPSIS, 0.983 with both ARAS and COPRAS, and a perfect 1.00 with WASPAS and MOORA. The high values showed that the DEAV model produced rankings considered significantly consistent with those generated by established MADM methods, thereby validating the effectiveness and reliability in multi-criteria decision-making contexts.
3.2. The case study of the CNC turning process applied to ST37 steel
Computer Numerical Control (CNC) turning introduced in the 1950s has been widely used for producing precise and complex components across different industries. The technology enables high-precision and repeatable manufacturing processes by automating the control of machining tools through programmed instructions. This capability is specifically important in industries such as aerospace, automotive, and electronics, where stringent demands for precision and consistency are predominant. In aerospace, CNC turning manufactures components with tight tolerances which are important for safety and performance, while in automotive, it produces engine parts and transmission components with high precision. The electronics industry also benefits from CNC turning by producing intricate device components that require meticulous accuracy. This is due to the ability of CNC machine to enhance efficiency, reduce human error, and allow for the production of complex geometries unachievable with manual methods. Consequently, technology is a cornerstone of modern manufacturing, driving technological advancements and significantly improving product quality.
ST37 steel is a commonly used material in different industrial settings and considered the ideal subject for this study due to the extensive use and the complexity of the machining process. CNC turning of ST37 steel requires multiple responses, including surface roughness and material removal rate. These responses are critical to the overall performance and cost-effectiveness of the manufacturing process and are considered part of the challenging MRO problems. Therefore, some important steps are required to solve problem which include (1) preparing the ST37 steel specimens, (2) identifying the relevant factors with levels and responses, (3) applying Taguchi method for experimental design, and (4) determining the optimal parameters for machining using a novel DEAV-Taguchi method.
3.2.1. The results of the experiment conducted using Taguchi method
Table 7 The details of the other experimental results based on Taguchi method
Runs | S | F | D | Ra | MRR |
1 | 1000 | 0.06 | 0.1 | 1.790 | 548 |
2 | 1000 | 0.11 | 0.3 | 1.799 | 2,827 |
3 | 1000 | 0.16 | 0.5 | 1.895 | 6,087 |
4 | 2000 | 0.06 | 0.3 | 1.357 | 2,904 |
5 | 2000 | 0.11 | 0.5 | 1.382 | 7,209 |
6 | 2000 | 0.16 | 0.1 | 2.117 | 2,628 |
7 | 3000 | 0.06 | 0.5 | 1.349 | 7,025 |
8 | 3000 | 0.11 | 0.1 | 2.024 | 3,598 |
9 | 3000 | 0.16 | 0.3 | 2.013 | 10,525 |
Figure 7 The main effects plot for S/N ratios of the MRR response
The optimal parameters to achieve the desired Ra were found in Figure 6 to be a speed of 2000 rpm, a feed rate of 0.06 mm/rev, and a depth of cut of 0.5 mm. Meanwhile, the values to achieve the desired MRR were recorded to be 3000 rpm, 0.16 mm/rev, and 0.5 mm respectively in Figure 7. The ANOVA results for both responses are also presented in Tables 8 and 9, respectively.
Table 8 ANOVA for S/N ratios for the Ra response
Source | DF | Seq SS | Adj SS | Adj MS | F | P |
Speed | 2 | 2.5275 | 2.5275 | 1.26374 | 97.37 | 0.010 |
Feed rate | 2 | 10.2382 | 10.2382 | 5.11912 | 394.42 | 0.003 |
Dept of cut | 2 | 7.6113 | 7.6113 | 3.80567 | 293.22 | 0.003 |
Residual Error | 2 | 0.0260 | 0.0260 | 0.01298 |
|
|
Total | 8 | 20.4030 |
|
|
|
|
S | 2 | 2.5275 | 2.5275 | 1.26374 | 97.37 | 0.010 |
Table 9 ANOVA for S/N ratios for the MRR response
Source | DF | Seq SS | Adj SS | Adj MS | F | P |
Speed | 2 | 140.396 | 140.396 | 70.198 | 61.71 | 0.016 |
Feed rate | 2 | 97.103 | 97.103 | 48.551 | 42.68 | 0.023 |
Dept of cut | 2 | 219.880 | 219.880 | 109.940 | 96.65 | 0.010 |
Residual Error | 2 | 2.275 | 2.275 | 1.138 |
|
|
Total | 8 | 459.653 |
|
|
|
|
S | 2 | 140.396 | 140.396 | 70.198 | 61.71 | 0.016 |
The factors of speed (S), feed rate (F), and depth of cut (D) were found to have a significant effect on both the Ra and MRR responses, with P-values less than 0.05. This showed that the determination of the optimal parameters for the two conflicting responses presented a significant challenge due to the need to balance opposing objectives. Therefore, the MRO problem was planned to be solved through the proposed method. This was achieved by using the DEAV model to integrate the two responses for each experimental run into efficiency scores. Subsequently, the Minitab statistical software version 19 was applied to optimize the parameters for the CNC turning machine for ST37 steel based on Taguchi method. The detailed calculation steps of the proposed method are presented in the following section.
3.2.2. Determining the optimal parameters using the DEAV model with the sensitivity analysis and Taguchi method
The initial decision matrix was obtained as shown in Table 10. The purpose of the matrix was to be used in calculating the efficiency scores of the DMUs or runs using the following steps:
Table 10 The initial decision matrix for the case study
Runs | Ra (µm) | MRR (mm3/min) |
1 | 1.790 | 548 |
2 | 1.799 | 2,827 |
3 | 1.895 | 6,087 |
4 | 1.357 | 2,904 |
5 | 1.382 | 7,209 |
6 | 2.117 | 2,628 |
7 | 1.349 | 7,025 |
8 | 2.024 | 3,598 |
9 | 2.013 | 10,525 |
(1) The efficiency scores of each DMU using the DEAV model
Sensitivity analysis was used to ascertain the weight of each criterion. This was achieved through the application of the weight adjustment method across nine scenarios to examine the impact of different weight distributions on the criteria. The scenarios are presented as follows:
Scenario#1: Allocation of 90% to the Ra response and 10% to the MRR response.
Scenario#2: Allocation of 80% to the Ra response and 20% to the MRR response.
Scenario#3: Allocation of 70% to the Ra response and 30% to the MRR response.
Scenario#4: Allocation of 60% to the Ra response and 40% to the MRR response.
Scenario#5: Equal allocation of 50% to the Ra response and 50% to the MRR response.
Scenario#6: Allocation of 40% to the Ra response and 60% to the MRR response.
Scenario#7: Allocation of 30% to the Ra response and 70% to the MRR response.
Scenario#8: Allocation of 20% to the Ra response and 80% to the MRR response.
Scenario#9: Allocation of 10% to the Ra response and 90% to the MRR response.
The DEAV model was used to integrate the two responses into a single efficiency score for each run. These efficiency scores were analyzed using the Taguchi method in Minitab version 19 to determine the optimal parameters for the CNC turning process. Model (2) was used to calculate the efficiency of each DMU, which in this context was represented by each run. The DEAV model was implemented using Lingo software with relevant parameters, including the Ra, MRR, and the weights for each response, integrated into the Lingo code. An example of the efficiency calculation for Scenario#5 presented in Table 11 shows the step-by-step process and methods used to determine the efficiency scores of each DMU within the given scenario. This was necessary to clarify how the input and output variables were processed and the application of the criteria weights determined through sensitivity analysis to generate the final efficiency scores.
Table 11 The details of the Lingo code for Scenario#5
Lingo code for the DEAV model |
MODEL: SETS: ALTERNATIVE/1..9/: ; CRITERION/1..2/:w; DMU/1..9/: E,u,v; IJ(ALTERNATIVE, CRITERION): X; ENDSETS DATA: X= 1.790, 548 1.799, 2827 1.895, 6087 1.357, 2904 1.382, 7209 2.117, 2628 1.349, 7025 2.024, 3598 2.013, 10525; N_inputs=1; w= 0.50, 0.50; !w={wi,wr); ENDDATA MAX = @SUM(DMU (K): E(K)); @FOR(DMU(K):E(K) = @SUM(CRITERION(J)|j#GT# N_inputs :u(K)*(X(K,J)^w(J) )) ); Constraints; @FOR(DMU(K): @SUM(CRITERION(J)|J#LE#N_inputs :v(K)*(X(K, J)^w(J) )) = 1 ); @FOR(DMU(K): @FOR(ALTERNATIVE(I): @SUM(CRITERION(J)|j#GT#N_inputs :u(K)*(X(I, J)^w(J) )) <= @SUM(CRITERION(J)|J#LE# N_inputs :@SUM(CRITERION(J):v(K)*(X(I, J)^w(J))) ))); @FOR(DMU(K): u(K)>=0); END |
Table 12 The ranking comparison of the proposed DEAV model against established MADM methods
Runs | Parameters | Ra (µm) | MRR (mm3/min) | Ekk |
1 | S1: F1: D1 | 1.790 | 548 | 0.2420 |
2 | S1: F2: D2 | 1.799 | 2,827 | 0.5482 |
3 | S1:F3: D3 | 1.895 | 6,087 | 0.7838 |
4 | S2:F1: D2 | 1.357 | 2,904 | 0.6398 |
5 | S2: F2: D3 | 1.382 | 7,209 | 0.9988 |
6 | S2: F3: D1 | 2.117 | 2,628 | 0.4873 |
7 | S3: F1:D3 | 1.349 | 7,025 | 0.9980 |
8 | S3: F2: D1 | 2.024 | 3,598 | 0.5831 |
9 | S3: F3: D2 | 2.013 | 10,525 | 1.0000 |
The execution of the Lingo code led to the determination of the efficiency scores (Ekk) for Scenario #5 in Table 12. This was followed by the application of the larger-is-better criterion of Taguchi to identify the optimal parametric conditions. The S/N Ratios of the Ekk response are presented in Table 13.
Table 13 Response table for S/N Ratios of the Ekk response
Experiment | S | F | D |
1 | -6.5537 | -5.4072 | -7.7515 |
2 | -3.3782 | -3.3054 | -3.0335 |
3 | -1.5676 | -2.7869 | -0.7145 |
Delta | 4.9862 | 2.6203 | 7.0370 |
Rank | 2 | 3 | 1 |
The higher delta value presented in the table shows that process parameters have a more significant impact on the multi-response performance indicator. Consequently, the delta statistics showed that the Ekk response was most influenced by the depth of cut (D), followed by speed (S), and then feed rate (F). It is important to state that the main effects plot for S/N ratios are shown in Figure 8. The method ensured the selected parameters achieved the maximum desired outcomes, offering a robust framework for optimizing the CNC turning process of ST37 steel.
Figure 8 The main effects
plot for S/N ratios of the Ekk
The analysis showed that the optimal
parameters to achieve the desired Ekk were a speed of 3,000
rpm, a feed rate of 0.16 mm/rev, and a depth of cut of 0.5 mm. Moreover, the
ANOVA results for the Ekk response are presented in Table 14.
Table 14 ANOVA for S/N ratios for the Ekk response
|
Source |
DF |
Seq SS |
Adj SS |
Adj MS |
F |
P |
|
Speed |
2 |
38.224 |
38.2242 |
19.1121 |
83.82 |
0.012 |
|
Feed rate |
2 |
11.552 |
11.5525 |
5.7762 |
25.33 |
0.038 |
|
Depth of cut |
2 |
77.158 |
77.1575 |
38.5788 |
169.20 |
0.006 |
|
Residual Error |
2 |
0.456 |
0.4560 |
0.2280 |
|
|
|
Total |
8 |
127.390 |
|
|
|
|
|
S |
2 |
38.224 |
38.2242 |
19.1121 |
83.82 |
0.012 |
The efficiency scores Ekk
for each run, derived from the DEAV model calculations, were subjected to
ANOVA. The analysis showed that the factors of speed (S), feed rate (F),
and depth of cut (D) significantly influenced the Ekk
response at P-values less than 0.05, showing strong statistical significance.
(1)
Sensitivity analysis
Sensitivity analysis is a
method widely used to ensure the reliability and stability of solutions.
Therefore, a comprehensive two-phase sensitivity analysis was adopted in this
study. In the first phase, nine scenarios were developed to model different weights
of criteria with a reflection of the emphasis on the Ra value over the MRR
value. This was achieved using the weight adjustment method as stated in Step
(1) to examine the impact of different weight distributions on the criteria.
The same calculation steps applied to evaluate the Ekk as in Scenario #5 were used for other scenarios with the results
presented in Table 15.
Table 15 The
efficiency scores (Ekk) for all scenarios
|
Ekk |
|||||||||
|
Sc.#1 |
Sc.#2 |
Sc. #3 |
Sc. #4 |
Sc. #5 |
Sc.#6 |
Sc.#7 |
Sc. #8 |
Sc. #9 |
|
|
1 |
0.6007 |
0.4788 |
0.3816 |
0.3042 |
0.2420 |
0.1780 |
0.1309 |
0.0963 |
0.0708 |
|
2 |
0.7046 |
0.6621 |
0.6221 |
0.5846 |
0.5482 |
0.4753 |
0.4121 |
0.3573 |
0.3098 |
|
3 |
0.7260 |
0.7404 |
0.7551 |
0.7701 |
0.7838 |
0.7376 |
0.6941 |
0.6531 |
0.6146 |
|
4 |
0.9106 |
0.8341 |
0.7640 |
0.6998 |
0.6398 |
0.5407 |
0.4570 |
0.3863 |
0.3265 |
|
5 |
0.9810 |
0.9859 |
0.9909 |
0.9958 |
0.9988 |
0.9262 |
0.8589 |
0.7965 |
0.7386 |
|
6 |
0.6042 |
0.5728 |
0.5431 |
0.5150 |
0.4873 |
0.4263 |
0.3729 |
0.3262 |
0.2854 |
|
7 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
0.9980 |
0.9208 |
0.8497 |
0.7840 |
0.7234 |
|
8 |
0.6492 |
0.6323 |
0.6159 |
0.5999 |
0.5831 |
0.5240 |
0.4710 |
0.4233 |
0.3804 |
|
9 |
0.7263 |
0.7871 |
0.8531 |
0.9246 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
The efficiency values of all scenarios were
subsequently utilized to calculate the optimal parameters and predicted Taguchi
results for each case using Minitab version 19. Therefore, Table 16 presents
the optimal parameters with the predicted responses of alternatives for the
nine scenarios. Table
16 focuses on selecting the most suitable experimental outcomes, with a clear
prioritization of MRR over Ra. Optimization strategy aims to maximize MRR,
achieving 10,603 mm³/min while maintaining Ra at 1.851 µm. Moreover, the
optimal parameters identified were a speed of 3000 rpm, a feed rate of 0.16
mm/rev, and a depth of cut of 0.5 mm. These "optimal parameters" were
determined through the Taguchi method, targeting the best settings to enhance
overall machining efficiency and performance. The predicted values labeled
"Predict Taguchi results" were further obtained using Minitab version
19 to forecast the outcomes based on the determined parameter settings.
Table 16 A
comprehensive comparison of the optimal parameters across nine distinct
scenarios
|
Scenarios |
Original parameters |
Optimal parameters |
Predict Taguchi results |
|
|
Ra (µm) |
MRR (mm3/min) |
|||
|
Scenario#
1 |
S3: F1: D3 |
S2: F1: D3 |
1.165 |
4,879 |
|
Scenario#
2 |
S3: F1: D3 |
S3: F2: D3 |
1.578 |
8,734 |
|
Scenario#
3 |
S3: F1: D3 |
S3: F2: D3 |
1.578 |
8,734 |
|
Scenario#
4 |
S3: F1: D3 |
S3: F3: D3 |
1.851 |
8,766 |
|
Scenario#
5 |
S3: F3: D2 |
S3: F3: D3 |
1.851 |
10,603 |
|
Scenario#
6 |
S3: F3: D2 |
S3: F3: D3 |
1.851 |
10,603 |
|
Scenario#
7 |
S3: F3: D2 |
S3: F3: D3 |
1.851 |
10,603 |
|
Scenario#
8 |
S3: F3: D2 |
S3: F3: D3 |
1.851 |
10,603 |
|
Scenario#
9 |
S3: F3: D2 |
S3: F3: D3 |
1.851 |
10,603 |
The optimal
parameters S3:F3:D3 were selected when the importance weight of the MRR
criterion was equal to or greater than for the Ra criterion. However, in a
situation where the Ra criterion had more significance, the optimal parameters
were changed. For example, in Scenario #3, the optimal parameters shifted to
S3:F2:D3 when 70% weight was on the Ra response and 30% on the MRR response. In
scenarios where the Ra response was significantly prioritized over the MRR
criterion, such as in Scenario #1, the optimal parameters were adjusted to a
speed of 2000 rpm, a feed rate of 0.06 mm/rev, and a depth of cut of 0.5 mm.
This showed the choice of parameters mainly depended on the required surface
finish quality for specific applications.
The
second phase was focused on using different MADM methods for a comparative
analysis through the application of the data obtained from the DEAV model in
Section 3.2.2.1. The decision matrix from Table 5 with weights assigned as wRa = 0.50 and wMRR = 0.50 were used for the
analysis. The detailed comparison of the proposed method with other MADM such
as TOPSIS (Hwang et al., 1981),
WASPAS (Zavadskas et al., 2012), and
ARAS (Zavadskas and Turskis, 2010), COPRAS (Zavadskas,
Kaklauskas, and Šarka, 1994), DEAR (Liao and
Chen, 2002; Kamath et al., 2022),
and MOORA with the full multiplicative form (Brauers
and Zavadskas, 2010) is presented in Table 17. This was necessary to
determine the effectiveness and robustness of the proposed solution.
Table 17 A
comprehensive comparison of the optimal parameters across various MADM methods
|
Methods |
Original
parameters |
Optimal
parameters |
|
|
Proposed |
S3: F3: D2 |
S3: F3: D3 |
|
|
TOPSIS |
S3: F3: D2 |
S3: F3: D3 |
|
|
WASPAS |
S3: F3: D2 |
S3: F3: D3 |
|
|
ARAS |
S3: F3: D2 |
S3: F3: D3 |
|
|
COPRAS |
S3: F3: D2 |
S3: F3: D3 |
|
|
DEAR |
S3: F3: D2 |
S3: F3: D3 |
|
|
MOORA |
S3: F3: D2 |
S3: F3: D3 |
The comparison showed
that the optimal parameters identified were consistent (S3:F3:D3) across the
majority of MADM methods. This consistency further confirmed the robustness and
reliability of the methods in optimizing the parameters for the CNC turning
process of ST37 steel. The uniformity across different MADM methods also
suggests the parameters are optimal to achieve the desired performance metrics.
The
ranking alternatives of the DEAV model were compared with different MADM
methods using the original parameters, specifically the decision matrix from
Table 10, with weights wRa = 0.50 and wMRR = 0.50. The
results obtained from the comparison process are presented in Table 18 while
the Spearman correlation coefficients are shown in Figure 9.
Table 18 The
ranking comparison of the proposed DEAV model against established MADM methods
|
Run |
DEAV |
Rank |
TOPSIS |
Rank |
WASPAS |
Rank |
ARAS |
Rank |
COPRAS |
Rank |
MOORA |
Rank |
|
1 |
0.2420 |
9 |
0.0936 |
9 |
0.3005 |
9 |
0.3225 |
9 |
0.3505 |
9 |
0.3102 |
9 |
|
2 |
0.5482 |
7 |
0.2415 |
7 |
0.4790 |
7 |
0.4541 |
7 |
0.5052 |
7 |
0.7028 |
7 |
|
3 |
0.7838 |
4 |
0.5395 |
4 |
0.6434 |
4 |
0.6298 |
4 |
0.7130 |
4 |
1.0048 |
4 |
|
4 |
0.6398 |
5 |
0.3070 |
5 |
0.5794 |
5 |
0.5528 |
5 |
0.6119 |
5 |
0.8202 |
5 |
|
5 |
0.9988 |
2 |
0.6803 |
2 |
0.8241 |
3 |
0.7972 |
2 |
0.8997 |
2 |
1.2805 |
2 |
|
6 |
0.4873 |
8 |
0.2010 |
8 |
0.4212 |
8 |
0.3991 |
8 |
0.4448 |
8 |
0.6247 |
8 |
|
7 |
0.9980 |
3 |
0.6642 |
3 |
0.8254 |
2 |
0.7957 |
3 |
0.8970 |
3 |
1.2794 |
3 |
|
8 |
0.5831 |
6 |
0.2970 |
6 |
0.4908 |
6 |
0.4670 |
6 |
0.5235 |
6 |
0.7475 |
6 |
|
9 |
1.0000 |
1 |
0.8254 |
1 |
0.8268 |
1 |
0.8728 |
1 |
1.0000 |
1 |
1.2820 |
1 |
Figure 9 The Spearman
correlation coefficients for optimizing CNC turning of ST37 steel
(3)
Experimental validation
A
confirmation test was conducted using the optimal parameters identified by the
proposed method, which were a speed of 3000 rpm, a feed rate of 0.16 mm/rev,
and a depth of cut of 0.5 mm. The results showed that the predicted Ra and MRR
values were 1.851µm and 10,603 mm3/min as presented in Table 14. The
optimal parameters were tested in 12 replications and the results were close to
the actual experiment within 95% confidence level as shown in Table 19.
Table 19 Confirmation
test at 95% confidence interval (CI).
|
Responses |
95% CI |
Means |
Predicted |
|
|
Low |
High |
|||
|
Ra |
1.752 |
1.858 |
1.805 |
1.851 |
|
MRR |
10611 |
10763 |
10,687 |
10,603 |
Figure 9 The Spearman
correlation coefficients for optimizing CNC turning of ST37 steel
In conclusion, MRO was found to be important
in modern manufacturing, where achieving efficiency and quality required
considering multiple performance metrics simultaneously. The need for
innovative strategies was due to the fact that traditional optimization methods
often struggled to balance conflicting objectives. This study presented a novel
hybrid method for MRO by combining the DEAV model with Taguchi method. The DEAV
model was used to improve on traditional DEA by incorporating MADM principles,
offering a comprehensive evaluation of performance metrics. Taguchi method was
later used to optimize parameters based on the efficiency scores of the DEAV
model.
The
proposed method was a systematic process initiated through the identification
of relevant factors, determination of the critical variables influencing
process outcomes, and the subsequent respective levels. Taguchi method was
applied to design experiments using orthogonal arrays in order to efficiently
study the effects of multiple variables. Subsequently, the DEAV model was
formulated to convert response values into a single efficiency score for each
experimental run. Optimization was achieved by analyzing these efficiency
scores using Taguchi method to identify optimal parameters based on
signal-to-noise (S/N) ratios. The method was later validated through numerical
examples by optimizing a fish scale scraping machine and the CNC turning
process of ST37 steel.
The
results showed that the DEAV-Taguchi method provided more efficient and
reliable outcomes than existing methods. Specifically, it significantly
improved scaling efficiency by 15% and reduced fish damage by 10% for the fish
scale scraping machine. For the CNC turning process of ST37 steel, the method
enhanced surface roughness by 10.33% through a reduction from 2.013 µm
to 1.805 µm and increased the material removal rate (MRR) by 1.54% from 10,525
mm3/min to 10,687 mm³/min.
This
study contributed a robust and adaptable optimization framework that integrates
DEA and MADM principles with the systematic Taguchi method, effectively
addressing MRO complexities and demonstrating versatility across different
manufacturing processes. However, the findings were limited to specific
applications, such as a fish scale scraping machine and CNC turning of ST37
steel, suggesting a need for further experiments to validate broader
applicability across materials and processes. Economic impacts of optimized
parameters were also not fully explored, signalling the need for future
research to assess these dimensions for improved practical value. The
integration of MADM and Taguchi required careful consideration of inherent
limitations, urging future studies to address potential biases for greater
reliability. Key recommendations include validating the method with diverse
materials and processes, expanding experimental designs to better understand
parameter interactions, and assessing economic and environmental impacts to
enhance sustainability insights. Additionally, combining the DEAV model with
other optimization and weighting techniques (e.g., CRITIC, Entropy, AHP, BWM)
could increase adaptability and robustness, expanding the model's relevance in
MADM scenarios by supporting more nuanced, criteria-based decision-making for
complex industrial applications.
The author wishes to extend heartfelt
gratitude to Kalasin University, Udonthani Rajabhat University, and Rajabhat
Rajanagarindra University for their invaluable support and resources, which
were instrumental in conducting this study. Additionally, the author expresses
sincere appreciation to the reviewers for their thoughtful feedback and
constructive suggestions, which significantly enriched the quality and rigor of
this research.
Conflict of Interest
The
authors declared that there was no known competing financial interests or
personal relationships capable of influencing the results reported in this
study.
| Filename | Description |
|---|---|
| R1-IE-7134-20240717160642.jpg | --- |
Abdelaoui, F.Z.E., Jabri, A., Barkany, A. E., 2023. Optimization Techniques for Energy Efficiency In Machining Processes—A Review. The International Journal of Advanced Manufacturing Technology, Volume 125(7), pp. 2967–3001
Brauers, W.K.M., Zavadskas, E.K., 2010. Project Management by MULTIMOORA As an Instrument for Transition Economies. Technological and Economic Development of Economy, Volume 16(1), pp. 5–24. https://doi.org/10.3846/TEDE.2010.01
Charnes, A., Cooper, W.W., Rhodes, E., 1978. Measuring The Efficiency of Decision-Making Units. European Journal of Operational Research, Volume 2(6), pp. 429–444. https://doi.org/10.17485/IJST%2F2012%2FV5I12%2F30612
Chen, W.H., Huang, T.H., Luo, D., Jin, L., Maduabuchi, C., Lamba, R., Hoang, A. T., 2024. Optimization of a Unileg Thermoelectric Generator by the Combination of Taguchi Method and Evolutionary Neural Network for Green Power Generation. Applied Thermal Engineering, Volume 248, p. 123204.
https://doi.org/10.1016/j.applthermaleng.2024.123204
Fan, Y., Bai, B., Qiao, Q., Kang, P., Zhang, Y., Guo, J., 2017. Study On Eco-Efficiency of Industrial Parks in China Based on Data Envelopment Analysis. Journal of Environmental Management, Volume 192, pp.107–115.
.https://doi.org/10.1016/j.jenvman.2017.01.048
Hwang, C.L., Yoon, K., Hwang, C.L., Yoon, K., 1981. Methods For Multiple Attribute Decision Making: Lecture Notes in Economics and Mathematical Systems. Springer-Berlin, Heidelberg, Volume186, pp. 58–191.
https://doi.org/10.1016/0377-2217%2888%2990267-6
Kamath, G. B., Subramaniam, K., Devesh, S., Chavan, V., Mohan, N., Bhat, R., Wijerathne, H. T., 2022. Multi-Response Optimization of Milling Process Parameters for Aluminium-Titanium Diboride Metal Matrix Composite Machining Using Taguchi-Data Envelopment Analysis Ranking Approach. Engineered Science, Volume 18, pp. 271–277. http://dx.doi.org/10.30919/es8d680
Kannan, S., Varatharajulu, M., Hariharasakthisudhan, P., Logesh, K., 2023. Identification of the Effect of Strontium and Ytterbium Addition Over Magnesium Zinc Alloy During the Drilling Process with ARAS And WASPAS Techniques. Materials Chemistry and Physics, Volume 309, p. 128320. https://doi.org/10.1016/j.matchemphys.2023.128320
Kantasiri, T., Kasemsiri, P., Pongsa, U., Posi, P., Chindaprasirt, P., 2024. Optimization of Concrete Containing Waste Crumb Rubber Mix Design for Thermal Insulating Applications Using Taguchi Method. Construction and Building Materials, Volume 434, p. 136636. https://doi.org/10.1016/j.conbuildmat.2024.136636
Kumar, R., Kumar, S., A?bulut, Ü., Gürel, A.E., Alwetaishi, M., Shaik, S., Saleel, C.A., Lee, D., 2024. Parametric Optimization of an Impingement Jet Solar Air Heater for Active Green Heating in Buildings Using Hybrid CRITIC-COPRAS Approach. International Journal of Thermal Sciences, Volume 197, p. 108760.
https://doi.org/10.1016/j.ijthermalsci.2023.108760
Kumar, R.S., Kumar, S.D., Rajkumar, S., 2022. Multi-Response Optimization of AISI H11 Using Taguchi and Grey Relational Analysis. Materials Research Express, Volume 9(10), p. 106508. https://doi.org/10.1088/2053-1591%2Fac95fe
Lestari, W.D., Adyono, N., Faizin, A.K., Haqiyah, A., Sanjaya, K.H., Nugroho, A., Kusmasari, W., Ammarullah, M.I., 2024. Optimization Of 3D Printed Parameters for Socket Prosthetic Manufacturing Using the Taguchi Method and Response Surface Methodology. Results in Engineering, Volume 21, p. 101847. https://doi.org/10.1016/j.rineng.2024.101847
Li, F., Zhu, Q., Chen, Z., Xue, H., 2018. A Balanced Data Envelopment Analysis Cross-Efficiency Evaluation Approach. Expert Systems with Applications, Volume 106, pp. 154–168. https://doi.org/10.1108/dta-01-2020-0003
Li, M.J., Lu, J.C., Chen, L., 2022. A Method to Determine the Integrated Weights of Cross-Efficiency Aggregation. Soft Computing, Volume 26(14), pp. 6825–6837. https://doi.org/10.1007/s00500-022-06926-y
Liao, H.C., Chen, Y.K., 2002. Optimizing Multi-Response Problem in the Taguchi Method by DEA-Based Ranking Method. International Journal of Quality & Reliability Management, Volume 19(7), pp. 825–837. https://doi.org/10.1108/02656710210434766
Liu, M., Duan, C., Li, G., Cai, Y., Wang, F., Li, L., 2023. Multi-Response Optimization of Ni-Based Laser Cladding via Principal Component Analysis and Grey Relational Analysis. Optik, Volume 287, p.171122. https://doi.org/10.1016/j.ijleo.2023.171122
Moganapriya, C., Rajasekar, R., 2023. Dry Machining Characteristics of Coated Inserts and Multi-Response Optimization Through DEAR-Taguchi Method. Materialwissenschaft und Werkstofftechnik, Volume 54(6), pp. 751–760. https://doi.org/10.1002/mawe.202200166
Pawaree, N., Phokha, S., Phukapak, C., 2024. Multi-Response Optimization of Charcoal Briquettes Process for Green Economy Using a Novel TOPSIS Linear Programming and Genetic Algorithms Based on Response Surface Methodology. Results in Engineering, Volume 22, p. 102226. https://doi.org/10.1016/j.rineng.2024.102226
Shi, H., Wang, Y., Zhang, X., 2019. A Cross-Efficiency Evaluation Method Based on Evaluation Criteria Balanced on Interval Weights. Symmetry, Volume 11(12), p. 1503. https://doi.org/10.3390/sym11121503
Shi, H.L., Chen, S.Q., Chen, L., Wang, Y.M., 2021. A Neutral Cross-Efficiency Evaluation Method Based on Interval Reference Points in Consideration of Bounded Rational Behavior. European Journal of Operational Research, Volume 290(3), pp. 1098–1110. https://doi.org/10.1016/j.ejor.2020.08.055
Shivakumar, M.R., Panchangam, M.K., 2024. Multi-Response Optimization of Reinforcement Parameters of Aluminum Alloy Composites by Taguchi Method and Grey Relational Analysis. Heliyon, Volume 10(9), p. e30183.
https://doi.org/10.1016/j.heliyon.2024.e30183
Soori, M., Arezoo, B., Dastres, R., 2023. Machine Learning and Artificial Intelligence in CNC Machine Tools: A Review. Sustainable Manufacturing and Service Economics, Volume 2, p. 100009. https://doi.org/10.1016/j.smse.2023.100009
Sriburum, A., Wichapa, N., Khanthirat, W., 2023. A Novel TOPSIS Linear Programming Model Based on the Taguchi Method for Solving the Multi-Response Optimization Problems: A Case Study of a Fish Scale Scraping Machine. Engineered Science, Volume 23, p. 882.
https://doi.org/10.30919/es882
Sristi, N.A., Zaman, P.B., Dhar, N.R., 2022. Multi-Response Optimization of Hard Turning Parameters: A Comparison Between Different Hybrid Taguchi-Based MCDM Methods. International Journal on Interactive Design and Manufacturing, Volume 16(4), pp.1779–1795. https://doi.org/10.1007/s12008-022-00849-6
Sulaiman, S., Alajmi, M.S., Isahak, W.N.W., Yusuf, M., Sayuti, M., 2022. Dry Milling Machining: Optimization of Cutting Parameters Affecting Surface Roughness of Aluminum 6061 using the Taguchi Method. International Journal of Technology, Volume 13(1), pp. 291–319. https://doi.org/10.14716/ijtech.v13i1.4208
Parr, W. C., 1989. Introduction to Quality Engineering: Designing Quality Into Products and Processes. Technometrics, Volume 31(2), pp.255–256. https://doi.org/10.1080/00401706.1989.10488520.
To-on, P., Wichapa, N., Khanthirat, W., 2023. A Novel TOPSIS Linear Programming Model Based on Response Surface Methodology for Determining Optimal Mixture Proportions of Lightweight Concrete Blocks Containing Sugarcane Bagasse Ash. Heliyon, Volume 9(7), p. e17755. https://doi.org/10.1016/j.heliyon.2023.e17755
Vellaiyan, S., Amirthagadeswaran, K.S., Sivasamy, D. B., 2018. Taguchi-Grey Relation Based Multi-Response Optimization of Diesel Engine Operating Parameters with Water-in-Diesel Emulsion Fuel. International Journal of Technology, Volume 9(1), pp. 68–77. https://doi.org/10.14716/IJTECH.V9I1.1374
Wang, C.N., Nguyen, X. T., Wang, Y.H., 2016. Automobile Industry Strategic Alliance Partner Selection: The Application of a Hybrid DEA and Grey Theory Model. Sustainability, Volume 8(2), p. 173. https://doi.org/10.3390/SU8020173
Yang, B., Zhang, G., Ran, Y., Yu, H., 2019. Kinematic Modelling and Machining Precision Analysis of Multi-Axis CNC Machine Tools Based on Screw Theory. Mechanism and Machine Theory, Volume 140, pp. 538–552.
https://doi.org/10.1016/J.MECHMACHTHEORY.2019.06.021
Yang, W.C., Yang, J.Y., Kim, R.C., Om, M.S., Kim, U.H., Ri, W.S., Sok, S.H., 2023. Multi-Attribute Optimization and Influence Assessment Methodology of Casting Process Parameters Combined with Integrated MADM and Taguchi Method. The International Journal of Advanced Manufacturing Technology, Volume 129(1), pp. 681–695. https://doi.org/10.1007/s00170-023-12275-3
Yaser, E.K.M., Shunmugesh, K., 2019. Multi-Objective Optimization of Milling Process Parameters in Glass Fiber-Reinforced Polymer Via Grey Relational Analysis and Desirability Function. Materials Today: Proceedings, Volume 11, pp. 1015–1023. https://doi.org/10.1016/J.MATPR.2018.12.032
Zavadskas, E. K., Turskis, Z., 2010. A new additive ratio assessment (ARAS) method in multicriteria decision?making. Ukio Technologinis Ir Ekonominis Vystymas, Volume 16(2), pp.159–172. https://doi.org/10.3846/tede.2010.10
Zavadskas, E.K., Turskis, Z., 2010. A New Additive Ratio Assessment (ARAS) Method in Multicriteria Decision?Making. Technological and economic development of economy, Volume 16(2), pp.159–172. https://doi.org/10.3846/TEDE.2010.10
Zavadskas, E.K., Turskis, Z., Antucheviciene, J., Zakarevicius, A., 2012. Optimization of Weighted Aggregated Sum Product Assessment. Elektronika ir Elektrotechnika, Volume 122(6), pp. 3–6. https://doi.org/10.5755/J01.EEE.122.6.1810
Zavadskas, E.K., Turskis, Z., Kildien?, S., 2014. State of the Art Surveys of Overviews on MCDM/MADM Methods. Technological and Economic Development of Economy, Volume 20(1), pp. 165–179. https://doi.org/10.3846/20294913.2014.892037
Zhujani, F., Abdullahu, F., Todorov, G., Kamberov, K., 2024. Optimization of Multiple Performance Characteristics for CNC Turning of Inconel 718 Using Taguchi–Grey Relational Approach and Analysis of Variance. Metals, Volume 14(2), p. 186. https://doi.org/10.3390/met14020186
