Mechanical Loading of Anterior Cruciate Ligament in Different Strategies of Stop-Jump Landing

Knee and anterior cruciate ligament (ACL) are among the most injured parts of the body during sports activities. Therefore, this study aimed to evaluate knee torque and mechanical stress on ACL under various conditions of stop-jump landing, as well as identify risk factors for injury, and propose improved strategies. The stop-jump landing was modeled using anthropometric and kinematic data. Knee torque was calculated with the inverse dynamic method, and ACL stress was determined using a Finite Element Model (FEM). Different landing strategies were simulated, including variations in knee flexion at initial foot contact, as well as knee and hip angular displacement. The results showed based on mechanical stress analysis, females (6.30 MPa) had a higher probability of ACL injury compared to males (4.51 MPa). Increasing knee flexion at initial contact caused decreased knee torque and approximately a 7% reduction in ACL stress. Furthermore, increasing knee and hip angular displacement led to a decrease in knee torque, with a reduction in ACL stress by 44% and 11% respectively. To reduce the risk of ACL injury, it is recommended to increase knee flexion at initial contact as well as promote knee and hip angular displacement during landing.

Biomechanics; Finite element; Knee; Modelling; Stress

ACL injury is a common incident in sports activities, and numerous studies have indicated that the primary cause is non-contact mechanisms (Renstrom et al., 2008). These mechanisms often occur during activities such as rapid deceleration, lateral cuts, and improper landings (Widuchowski, Widuchowski, and Trzaska, 2007; Majewski, Susanne, and Klaus, 2006). Consequently, it is crucial to conduct biomechanical analyses of knee injuries to gain a better understanding of the mechanisms, identify risk factors, and develop prevention strategies (Pearle et al., 2017; Tsujii, Nakamura, and Horibe, 2017).

Previous studies have used various methods to examine the mechanisms of non-contact ACL injury (Alentorn-Geli et al., 2009; Renstrom et al., 2008). In this context, biomechanical factors in the sagittal plane, such as low flexion angles of knee and hip, play a significant role. Among these factors, knee flexion angle reportedly has the largest contribution to knee joint injury (Markström, Tengman, and Häger, 2023; Jeong, Choi, and Shin, Chaudhari, and Andriacchi, 2021; Thomas et al., 2020). Studies have demonstrated that the landing phase poses a higher risk of ACL injury compared to the take-off phase for both males and females. In particular, females have greater extension torque, less angular displacement in knee and hip, and a higher maximum vertical ground reaction force compared to males (Fältström et al., 2021; Söderman et al., 2020).

Biomechanical modeling is a viable method for obtaining kinetic and kinematic parameters during movement analysis (Triwardono et al., 2021; Ahmad et al., 2020). Therefore, several investigations have used this method in examining landings across various sports, yielding consistent results with experimental studies (McErlain-Naylor et al., 2021; Taborri et al., 2020). A significant relationship was reported between the angular velocity and hip flexion, the peak torque of knee extension, as well as the posterior and vertical components of the ground reaction force. Based on the observations, increasing knee flexion reduces the vertical force of the ground reaction and increases extensor torque (Warrener, Tamai, and Lieberman, 2021; Biscarini et al., 2020; Kellis and Kouvelioti, 2009). It was concluded that the primary cause of non-contact ACL injury was an increase in ground reaction force at low knee flexion angles (Mohammadi-Orangi et al., 2021).

    Although most previous investigations on sports movements have been experimental, some also used modeling and simulation methods which are powerful tools in various engineering studies (Asvial et al., 2023; Hamza et al., 2023). These methods have been used to investigate joint kinematics, soft tissue deformations, stress and strain analysis, as well as movement under specific loading conditions (Mirtavoosi et al., 2017; Peña et al., 2006; Moglo and Shirazi-Adl, 2003). Some studies have also explored injury mechanisms in sports movements (Lin et al., 2009; Beillas et al., 2004). However, the dynamic responses of the associated joints during intense activities or those entailing collisions, impacts, or strikes have not been thoroughly investigated, with only a limited number of studies preferring to use dynamic and finite element model (Lin et al., 2009; Shin, Chaudhari, and Andriacchi 2009; Beillas et al., 2004). These models have been used to investigate knee stress in some contact situations, but the application for estimating knee loadings, moments, and stress under different landing strategies is limited. Therefore, this study aimed to investigate the relationship between knee joint torque and ACL stress with lower limb kinematics under different stop-jump landing strategies. Strategies are frequently performed in sports and are associated with a high incidence of non-contact ACL injury (Renstrom et al., 2008). Due to the challenges associated with empirically analyzing various landing strategies, biomechanical modeling was used to investigate the risk factors for ACL injury under stop-jump landing simulations. Therefore, this study modeled landing phase of the stop-jump to compare knee joint torque in males and females and investigate the distribution of stress in ACL to compare the risk of injury under different landing strategies. 

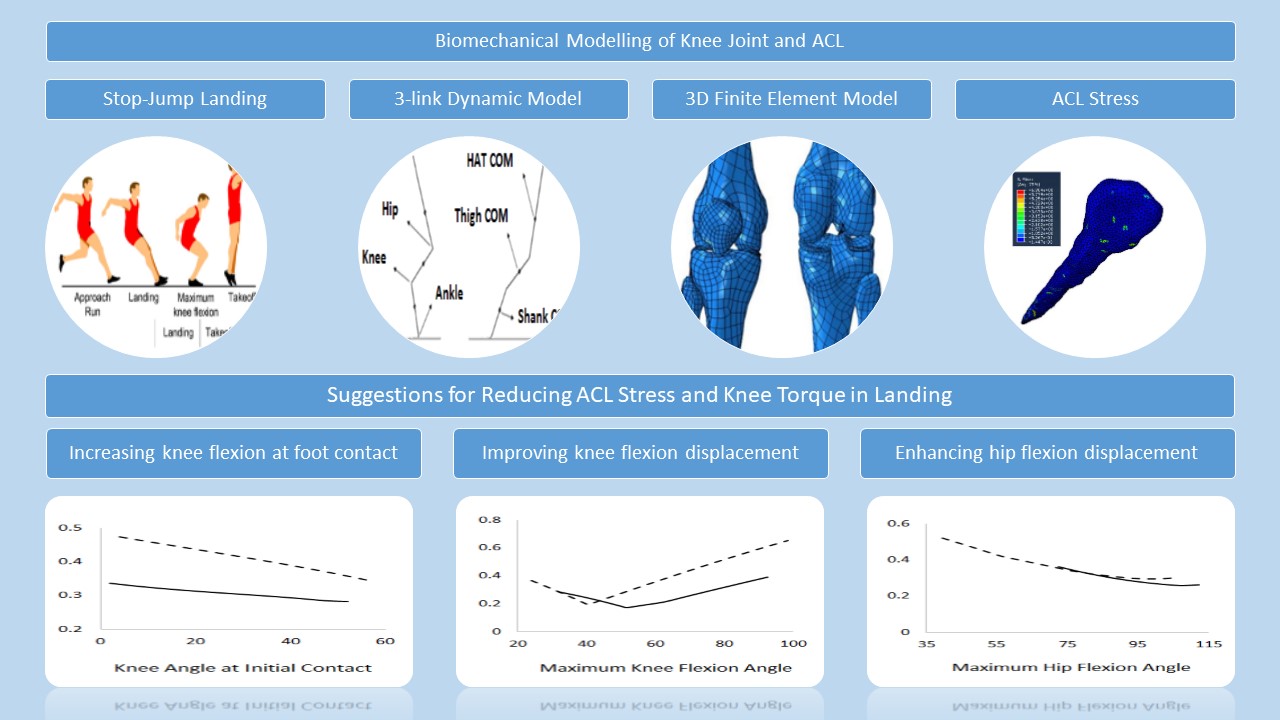
This study focused on landing phase of the stop-jump movement pattern. To achieve the objective, two biomechanical models were developed. The first model was a multi-link dynamic model used to calculate knee joint torque, while the second model was a finite element model used to analyze stress distribution in ACL. Using these models, different stop-jump landing strategies were simulated separately for both males and females. The first strategy entailed modifying knee flexion angle at the moment of initial foot contact. In the second strategy, the angular displacement of knee joint was altered during landing, while the third strategy included changing the angular displacement of the hip.

2.1. Multi-Link Dynamic Model

To construct a dynamic model of the athlete, the limbs and body joints were represented as rigid arms using the SimMechanics toolbox in MATLAB software (MATLAB R2010. Natick, MA: The MathWorks Inc). Anthropometric data provided the necessary information for model properties such as limb length, mass, and moment of inertia. For females, a model with an average height of 1.67 m and a weight of 559 N was created, while for males, a model with an average height of 1.78 m and a weight of 728 N was used. The data was based on anthropometric models described by a previous study and modified for Iranian athletes according to literature (Sadeghi, Mazloumi, and Kazemi, 2015).

The dynamic model consisted of three rigid links representing the shank, thigh, and HAT (head, arms, and trunk), as well as three hinged joints representing the ankle, knee, and thigh. The model was considered two-dimensional in the sagittal plane (Caruntu and Moreno, 2019). The inputs included the flexion angles of the hip, knee, and ankle joints at the moment of initial foot contact with the ground, the amount of displacement in these joints during the stop-jump landing, and landing time (Brown et al., 2008; Yu, Lin, and Garrett, 2006). Using the inverse dynamic method, motion was simulated, and knee joint torque was calculated during various stop-jump landing strategies. The torque values were divided by the product of weight and height. This normalization was performed to eliminate the influence of anthropometric properties on the results and facilitate comparison with other studies.

2.2. Finite Element Model (FEM)

The precise geometry and location were obtained from MR images in the sagittal section for soft tissues and from CT images in the transverse section for the bones. Initially, the image specifications, including size and spacing, were determined. The images from each section were processed to generate a three-dimensional geometric model of each knee structure. These geometric models were further refined by smoothing, noise reduction, and creating a shell model of the bones. Subsequently, knee joint structures were assembled using CATIA (CATIA V5, Dassault Systèmes). The 3D knee model was finally used in the ABAQUS finite element software (SIMULIA, ABAQUS, Dassault Systèmes) to analyze stress distribution of the ACL under different landing strategies, using corresponding torque input. In the finite element model depicted in Figure 1, the bones were considered rigid bodies (Peña et al., 2006; Beillas et al., 2004; Moglo and Shirazi-Adl, 2003) because the stiffness of these structures is much greater than that of soft tissues. Meanwhile, the soft tissues were modeled as deformable bodies. The two ends of ACL were connected to the femur and tibia using a tie with surface-to-surface interaction, and the coefficient of friction was set at 0.9 (Beillas et al., 2004). The femur was constrained in all six degrees of freedom, while the tibia was allowed to rotate around the internal-external axis.

Figure 1 The finite element model was developed using ABAQUS software

In the subsequent stage, the joint structures were meshed in preparation for analysis. Details regarding mechanical properties, element types, and mesh types for each knee joint structure are shown in Table 1 (Ruan et al., 2008; Beillas et al., 2004). To complete the analysis, the torque exerted on knee derived from the dynamic model, was applied as a load input. The solution was then obtained using the explicit dynamic method, allowing for the calculation of stress distribution in the ACL.

Table 1 Mechanical properties, element types, and mesh types for each knee joint structure

    The results of the dynamic model present knee joint torque obtained from simulating various stop-jump landing strategies. The kinematic data for both males and females were separately input into the multi-link dynamic model. Knee joint torque was then determined using the inverse dynamic method. As shown in Figure 2, the maximum normal torque of knee joint was found to be 0.43 for females and 0.30 for males. The results showed a strong correlation between torque values (r(13) = 0.949, p < 0.001), indicating similarity in overall knee joint torques during landing despite significant differences in peaks between males and females.

Figure 2 Normalized knee joint torque in males (solid line) and females (dashed line)

        Analysis of different landing strategies, depicted in Figure 3, showed that in the first strategy, increasing the flexion angle of knee joint at the moment of initial foot contact led to a decrease in the maximum torque for both males and females (Figure 3a). Furthermore, these results showed a strong negative correlation between maximum knee joint torques and angle of initial foot contact for both males (r(11) = -0.997, p < 0.001) and females (r(12) = -0.999, p < 0.001).

In the second strategy, as the angular displacement of knee joint increased, the maximum torque initially decreased until a minimum value was reached. However, beyond this point, an increase was observed (Figure 3b). An optimal value was identified for the maximum angle of knee flexion. For females and males, this optimal value was determined to be 40.5 degrees and 51.4 degrees, respectively. The results showed an overall strong correlation between angular displacement of knee joint and the maximum torque for both males (r(17) = 0.733, p < 0.001) and females (r(21) = 0.901, p < 0.001). Similarly, in the third strategy, an analogous behavior was observed. As the displacement of the hip angles increased, the maximum torque of knee joint initially decreased until reaching a minimum value and then increased. This led to the identification of optimal angles for maximum thigh flexion. For females and males, these optimal angles were determined to be 101.3 degrees and 107.3 degrees, respectively. The results also showed a strong negative correlation between angular displacement of the hip joint and the maximum torque of knee joint for both males (r(11) = -0.967, p < 0.001) and females (r(16) = -0.958, p < 0.001).

Figure 3 Maximum knee joint torque values in different stop-jump landing strategies. In the first strategy (a) knee angle at initial contact; in the second (b) the maximum knee flexion angle; and the third strategy (c) the maximum hip flexion angle was changed. Solid lines (-) represent males and dashed lines (- -) represent females

        The FEM results illustrate the distribution of ACL stress derived from solving the finite element model under different landing strategies. Using knee joint torque distribution obtained from the dynamic model, a finite element model was used to simulate the joint movement under the input torque. The result of this model determined stress distribution in ACL for both males and females. The maximum stress was found to be 6.30 MPa for females and 4.51 MPa for males. The temporal variation of the maximum stress distribution in ACL is shown in Figure 4.

Figure 4 Maximum stress distribution in ACL over time for males (solid line) and females (dashed line)

        Females experienced 1.40 times higher maximum stress than males, despite the overall time series of landing being similar between the two groups and showing a strong correlation (r(20) = 0.999, p < 0.001). The implementation of the finite element model illustrated in Figure 5 aimed to assess stress distribution in various landing strategies, showing that females had greater ACL stress than males. In the first strategy, stress distribution was analyzed for two different angles of knee flexion at the moment of initial foot contact. The maximum ACL stress at angles of 14° and 39° was 6.5 MPa and 6.1 MPa respectively (Figure 6a). In the second strategy, considering the maximum angles of knee flexion during landing to be 24° and 41°, the maximum stress in ACL was recorded as 2.5 MPa and 1.4 MPa respectively (Figure 6b). In the third strategy, as the amount of hip displacement increased, the maximum stress decreased. At maximum thigh flexion angles of 39° and 46°, the maximum stress in ACL was measured as 8.4 MPa and 7.4 MPa, respectively (Figure 6c). In all of these results, there were strong correlations between the time series of ACL stress for two selected values of initial knee angle, knee displacement, and hip displacement. The correlation coefficients were r(20) = 0.995, 0.771, and 1.000 with p < 0.001 for all three sets, respectively.

Figure 5 Simulation of the finite element model and the distribution of von Mises stress in ACL for (a) females and (b) males

        Stop-jump landing is frequently executed in basketball and volleyball and is linked to a high risk of ACL injury. The results show that gender differences in the kinetics of the lower limbs are consistent with previous empirical studies. Based on the dynamic model, females had greater knee joint torque than males, with a ratio of 1.43. According to mechanical theories, the possibility of injury is proportional to the value of joint torque. This suggests the risk of knee injury in females is higher than in males. Similarly, previous studies reported that the rate of ACL injury in female players was more than twice the rate among male players (Lin et al., 2009; Renstrom et al., 2008).

Figure 6 The maximum ACL stress distribution over time in different stop-jump landing strategies. In the first strategy (a), knee angles at initial contact are 14 (solid line) and 39 (dashed line). In the second strategy (b), the maximum knee flexion angles are 24 (solid line) and 41 (dashed line). In the third strategy (c), the maximum hip angles are 39 (solid line) and 46 (dashed line)

        According to previous studies, one of the effective factors in ACL injury is the low angle of knee flexion (Alentorn-Geli et al., 2009; Renstrom et al., 2008; Yu and Garrett, 2007; Pollard, Sigward, and Powers, 2007; Yu, Lin, and Garrett, 2006). This means that a decrease in the angle of knee flexion at initial contact leads to more joint damage and consequently ACL injury. The results not only showed the effect of the flexion angle on knee torque and ACL stress but also demonstrated that the values of these parameters in females were greater than in males. Based on the results, a lower flexion angle at initial contact leads to a larger torque production in knee joint. Through biomechanical analysis of the lower limb during drop landing, Yu et al. concluded that knee flexion angle was lower in females than in males (Yu, Lin, and Garrett, 2006). On the other hand, Chapple reported that knee torque in females during drop landing was higher, leading to the higher incidence of injury (Chappell et al., 2002). The model presented in this study based on mechanical relationship between flexion angle and kinetics of knee confirms and explains previous results.

        Through empirical studies on the standing long jump, Yu and Garret concluded that the large angles of knee and hip flexion during initial contact with the ground did not necessarily reduce the forces from impact. The impact could be rather attributed to the active movement of the joints (Yu and Garrett, 2007). This study, in simulating the second and third strategies, not only confirmed previous results but also provided optimal angles for maximum knee and hip flexion. In the standing long jump, the angular velocity of both joints affects the vertical and posterior components of ground reaction force inversely. This implies that as the angular velocity increases, the force component decreases. Meanwhile, Podraza and White showed that the greater the ground reaction force during landing, the greater the risk of non-contact ACL injury (Podraza and White, 2010). To reduce the ground reaction force, the angular velocity of knee and hip joints must be increased. Considering all ACL stress results were obtained at a constant landing time of 0.13 seconds, an increase in the displacement of knee and hip flexion was identical to elevation in the angular velocity in the two joints. Therefore, a decrease in the torque, as depicted in Figure 3, was in line with the results.

     The evaluation of the results obtained from the finite element model also confirmed the validity for estimating ACL stress during landing. Stress decreased with an increase in knee flexion angle at the initial contact of the foot. Therefore, ACL injury is affected by knee flexion angle at the initial contact of the foot, as also reported in previous studies (Alentorn-Geli et al., 2009; Renstrom et al., 2008; Yu and Garrett, 2007; Yu, Lin, and Garrett, 2006). The results also showed that increasing the displacement of knee and thigh joints during landing reduces stress on ACL and consequently mitigates the possibility of injury to the ligament. 

In conclusion, based on the results and previous empirical studies, the models developed can be used as effective tools for predicting the probability of injury in various landing strategies. From a technical and academic perspective, educators and stakeholders should advocate for specific strategies aimed at reducing ACL injury. Strategies comprise enhancing knee and hip biomechanics during landing tasks. Specifically, increasing knee flexion at the moment of initial foot contact, improving knee flexion displacement, and enhancing hip flexion displacement can help to reduce the risk of ACL injury. In general, these strategies facilitate shock absorption during landing, which in turn decreases torque on knee joint and subsequently lowers the risk of ACL injury in athletes.

Ahmad, M.A., Zulkifli, N.N.M.E., Shuib, S., Sulaiman, S.H., Abdullah, A.H., 2020. Finite Element Analysis of Proximal Cement Fixation in Total Hip Arthroplasty. International Journal of Technology, Volume 11(5), pp. 1046–1055

Alentorn-Geli, E., Myer, G.D., Silvers, H.J., Samitier, G., Romero, D., Lázaro-Haro, C., Cugat, R., 2009. Prevention of Non-Contact Anterior Cruciate Ligament Injuries in Soccer Players. Part 1: Mechanisms of Injury and Underlying Risk Factors. Knee Surgery, Sports Traumatology, Arthroscopy, Volume 17, pp. 705–729

Asvial, M., Zagloel, T.Y.M., Fitri, I.R., Kusrini, E., Whulanza, Y., 2023. Resolving Engineering, Industrial, and Healthcare Challenges through AI-Driven Applications. International Journal of Technology, Volume 14(6), pp. 1177–1184

Beillas, P., Papaioannou, G., Tashman, S., Yang, K.H., 2004. A New Method to Investigate in Vivo Knee Behavior using a Finite Element Model of the Lower Limb. Journal of Biomechanics, Volume 37, pp. 1019–1030

Biscarini, A., Contemori, S., Dieni, C.V., Panichi, R., 2020. Joint Torques and Tibiofemoral Joint Reaction Force in the Bodyweight “Wall Squat” Therapeutic Exercise. Applied Sciences, Volume 10(9), p. 3019

Brown, C., Padua, D., Marshall, S.W., Guskiewicz, K., 2008. Individuals with Mechanical Ankle Instability Exhibit Different Motion Patterns than those with Functional Ankle Instability and Ankle Sprain Copers. Clinical Biomechanics, Volume 23(6), pp. 822–831

Caruntu, D.I., Moreno, R., 2019. Human Knee Inverse Dynamics Model of Vertical Jump Exercise. Journal of Computational and Nonlinear Dynamics, Volume 14(10), p. 101005

Chappell, J.D., Yu, B., Kirkendall, D.T., Garrett, W.E., 2002. A Comparison of Knee Kinetics between Male and Female Recreational Athletes in Stop-Jump Tasks. The American Journal of Sports Medicine, Volume 30, pp. 261–267

Fältström, A., Kvist, J., Bittencourt, N.F.N., Mendonça, L.D., Hägglund, M., 2021. Clinical Risk Profile for a Second Anterior Cruciate Ligament Injury in Female Soccer Players After Anterior Cruciate Ligament Reconstruction. The American Journal of Sports Medicine, Volume 49(6), pp. 1421–1430

Hamza, S., Heidari, M., Ahmadizadeh, M., Dashtizadeh, M., Chitt, M., 2023. Modification of Horizontal Wind Turbine Blade: A Finite Element Analysis. International Journal of Technology, Volume 14(1), pp. 5–14

Jeong, J., Choi, D.-H., Shin, C.S., 2021. Core Strength Training Can Alter Neuromuscular and Biomechanical Risk Factors for Anterior Cruciate Ligament Injury. The American Journal of Sports Medicine, Volume 49, pp. 183–192

Kellis, E., Kouvelioti, V., 2009. Agonist Versus Antagonist Muscle Fatigue Effects on Thigh Muscle Activity and Vertical Ground Reaction During Drop Landing. Journal of Electromyography and Kinesiology, Volume 19(1), pp. 55–64

Lin, C.-F., Gross, M., Ji, C., Padua, D., Weinhold, P., Garrett, W.E., Yu, B., 2009. A Stochastic Biomechanical Model for Risk and Risk Factors of Non-Contact Anterior Cruciate Ligament Injuries. Journal of Biomechanics, Volume 42, pp. 418–423

Majewski, M., Susanne, H., Klaus, S., 2006. Epidemiology of Athletic Knee Injuries: A 10-Year Study. The Knee, Volume 13(3), pp. 184–188

Markström, J.L., Tengman, E., Häger, C.K., 2023. Side-Hops Challenge Knee Control in The Frontal and Transversal Plane More Than Hops for Distance or Height Among ACL-Reconstructed Individuals. Sports Biomechanics, Volume 22, pp. 142–159

McErlain-Naylor, S.A., King, M.A., Felton, P.J., 2021. A Review of Forward-Dynamics Simulation Models for Predicting Optimal Technique in Maximal Effort Sporting Movements. Applied Sciences, Volume 11(4), p. 1450

Mirtavoosi, S., Lenjannejadian, S., Khayambashi, K., Salehi, H., 2017. Finite Element Analysis of Anterior Talofibular Ligament under Different Strategies of Landing. Journal of Advanced Sport Technology, Volume 1(1), pp. 46–52

Moglo, K.E., Shirazi-Adl, A., 2003. On the Coupling Between Anterior and Posterior Cruciate Ligaments, and Knee Joint Response Under Anterior Femoral Drawer in Flexion: A Finite Element Study. Clinical Biomechanics, Volume 18, pp. 751–759

Mohammadi-Orangi, B., Yaali, R., Bahram, A., Aghdasi, M.T., Van-der-Kamp, J., Vanrenterghem, J., Jones, P.A., 2021. Motor Learning Methods That Induce High Practice Variability Reduce Kinematic and Kinetic Risk Factors of Non-Contact ACL Injury. Human Movement Science, Volume 78, p. 102805

Pearle, A.D., van der List, J.P., Lee, L., Coon, T.M., Borus, T.A., Roche, M.W., 2017. Survivorship and Patient Satisfaction of Robotic-Assisted Medial Unicompartmental Knee Arthroplasty at A Minimum Two-Year Follow-Up. The Knee, Volume 24, pp. 419–428

Peña, E., Calvo, B., Martínez, M.A., Doblaré, M., 2006. A Three-Dimensional Finite Element Analysis of The Combined Behavior of Ligaments and Menisci in The Healthy Human Knee Joint. Journal of Biomechanics, Volume 39(9), pp. 1686–1701

Podraza, J.T., White, S.C., 2010. Effect of Knee Flexion Angle on Ground Reaction Forces, Knee Moments and Muscle Co-Contraction During an Impact-Like Deceleration Landing: Implications for The Non-Contact Mechanism of ACL Injury. The Knee, Volume 17(4), pp. 291–295

Pollard, C.D., Sigward, S.M., Powers, C.M., 2007. Mechanisms of ACL Injury: Current Perspectives. Journal of Biomechanics, Volume 40, p. S254

Renstrom, P., Ljungqvist, A., Arendt, E., Beynnon, B., Fukubayashi, T., Garrett, W., Georgoulis, T., Hewett, T.E., Johnson, R., Krosshaug, T., Mandelbaum, B., Micheli, L., Myklebust, G., Roos, E., Roos, H., Schamasch, P., Shultz, S., Werner, S., Wojtys, E., Engebretsen, L., 2008. Non-contact ACL Injuries in Female Athletes: An International Olympic Committee Current Concepts Statement. British Journal of Sports Medicine, Volume 42, pp. 394–412

Ruan, J.S., El-Jawahri, R., Barbat, S., Rouhana, S.W., Prasad, P., 2008. Impact Response and Biomechanical Analysis of the Knee-Thigh-Hip Complex in Frontal Impacts with a Full Human Body Finite Element Model. Stapp Car Crash Journal, Volume 52, pp. 505–526

Sadeghi, F., Mazloumi, A., Kazemi, Z., 2015. An Anthropometric Data Bank for The Iranian Working Population with Ethnic Diversity. Applied Ergonomics, Volume 48, pp. 95–103

Shin, C.S., Chaudhari, A.M., Andriacchi, T.P., 2009. The Effect of Isolated Valgus Moments on ACL Strain During Single-Leg Landing: A Simulation Study. Journal of Biomechanics, Volume 42(3), pp. 280–285

Söderman, T., Wretling, M.-L., Hänni, M., Mikkelsen, C., Johnson, R.J., Werner, S., Sundin, A., Shalabi, A., 2020. Higher Frequency of Osteoarthritis in Patients with ACL Graft Rupture Than in Those with Intact ACL Grafts 30 Years After Reconstruction. Knee Surgery, Sports Traumatology, Arthroscopy, Volume 28, pp. 2139–2146

Taborri, J., Keogh, J., Kos, A., Santuz, A., Umek, A., Urbanczyk, C., Van-der-Kruk, E., Rossi, S., 2020. Sport Biomechanics Applications Using Inertial, Force, and EMG Sensors: A Literature Overview. Applied Bionics and Biomechanics, Volume 2020, pp. 1–18

Thomas, C., Dos’Santos, T., Comfort, P., Jones, P.A., 2024. Male and Female Soccer Players Exhibit Different Knee Joint Mechanics During Pre-Planned Change of Direction. Sports Biomechanics, Volume 23(1), pp. 118–131

Triwardono, J., Supriadi, S., Whulanza, Y., Saragih, A.S., Novalianita, D.A., Utomo, M.S., Kartika, I., 2021. Evaluation of the Contact Area in Total Knee Arthroplasty Designed for Deep Knee Flexion. International Journal of Technology, Volume 12(6), pp. 1312–1322

Tsujii, A., Nakamura, N., Horibe, S., 2017. Age-related changes in the knee meniscus. The Knee, Volume 24, pp. 1262–1270

Warrener, A., Tamai, R., Lieberman, D.E., 2021. The Effect of Trunk Flexion Angle on Lower Limb Mechanics During Running. Human Movement Science, Volume 78, p. 102817

Widuchowski, W., Widuchowski, J., Trzaska, T., 2007. Articular Cartilage Defects: Study of 25,124 Knee Arthroscopies. The Knee, Volume 14(3), pp. 177–182

Yu, B., Garrett, W.E., 2007. Mechanisms of Non-Contact ACL Injuries. British Journal of Sports Medicine, Volume 41, pp. 47–51

Yu, B., Lin, C.-F., Garrett, W.E., 2006. Lower Extremity Biomechanics During the Landing of a Stop-Jump Task. Clinical Biomechanics, Volume 21, pp. 297–305