Heuristic Approach to Planning Complex Multi-Stage Production Systems
Corresponding email: kapiton.pospelov@spbpu.com
Published at : 29 Dec 2023
Volume : IJtech
Vol 14, No 8 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i8.6833
Pospelov, K.N., Vatamaniuk, I.V., Lundaeva, K.A., Gintciak, A.M., 2023. Heuristic Approach to Planning Complex Multi-Stage Production Systems. International Journal of Technology. Volume 14(8), pp. 1790-1799
| Kapiton N. Pospelov | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Irina V. Vatamaniuk | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Karina A. Lundaeva | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Aleksei M. Gintciak | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
The
paper describes an algorithm for finding a quasi-optimal production plan for
complex production systems that involve moving products through a chain of
linked processes with varying resource sets. The general problem of optimizing
a network of manufacturing enterprises is considered: a set of enterprises
producing homogeneous products is modeled during a process consisting of a set
of sequential operations arranged in a strict sequence. Standard methods for solving
production planning problems are considered. According to the analytical
review, most planning tasks in such systems are resolved using original
techniques. For this reason, a universal heuristic algorithm was
proposed. An algorithm with two branches is also proposed for two cases: for
the case of a known constraint in the system and for an alternative case. The
algorithm is focused on application in production systems in which the acquisition
of empirical data is complicated by the large volume, heterogeneity, and
limited reliability of data. In such systems, quasi-optimization in accordance
with the proposed algorithm will allow for obtaining a satisfactory result with
the permissible and required computing power. The algorithm can be
classified as a greedy algorithm. It is partly based on local optimization and
performs well for production with a long cycle and a small number of products.
For this reason, the approach is recommended for heavy industry, shipbuilding,
aircraft manufacturing, and other productions with a long cycle.
Greedy algorithm; Heuristic techniques; Optimization algorithms; Production planning; Quasi-optimization
Selecting the scenario with the best load and resource distribution that satisfies various optimization criteria is necessary to achieve optimal production performance in a complex production system. To tackle the challenge of establishing an optimal production plan, one effective technique is the automation of production schedules. The introduction of ready-made digital solutions for schedule management is an expensive and difficult option in terms of adaptation to the conditions of a particular enterprise. Therefore, it is recommended to develop algorithms and software requirements tailored to optimize the production plan, considering the specific technological processes and resource constraints of the enterprise in question (Zakharenkov, Mrochek, and Mrochek, 2018). Mathematical techniques deployed to tackle uncomplicated tasks like assignments, workshop tasks, or other discrete and combinatorial optimization problems, can be considered conventional means to resolve production planning problems (Lee, Kim, and Kim 2023; Bengio, Lodi, and Prouvost, 2021). Such methods include linear optimization methods (Yazdani, Khezri, and Benyoucef, 2021), the Hungarian algorithm (Laha and Gupta, 2016), the branch-and-bound algorithm (Li and Qi, 2022), probability theory and simulation methods (Costas et al., 2023); stochastic optimization methods, for instance, swarm-based algorithms, are applicable to certain specific tasks (Zukhruf, Frazila, and Widhiarso, 2020). However, given the complexity of the problem within the framework presented, none of these methods is appropriate.
This
paper examines the general optimization problem for a network of manufacturing
enterprises: a set of enterprises producing similar products is modeled during
a process consisting of a set of consecutive operations arranged in a strict
sequence. The complexity of the task is heightened by diverse resource sets
linked to various processes and distinct resource requirements for different
products, rendering standard allocation solutions and simple linear
optimization algorithms impractical. In addition, when tackling a general task
of this nature, it is crucial to take production constraints – procedures that
are the chain's most ineffective link – into account. In some practical
instances of equivalent systems, the constraints are apparent, while in others,
they necessitate an analysis of the production processes.
At the same time, it is evident that the
mathematical formalization of production processes simplifies the real system
to a certain extent. Hence, the precision of the analytical solution to the
optimization issue in this scenario might not satisfy the decision-makers
requirements in regard to the balance between the result accuracy and
calculation expenses. Therefore, simplifying calculations is an essential task
when designing an algorithm to solve an optimization problem. Solutions
considering this aspect allow for a quasi-optimal (nearly optimal, although not
entirely precise) outcome.
This task is pertinent to enterprises that
undertake a few typical but time-consuming orders, specifically in heavy
industry, shipbuilding, and aircraft construction.
The aim of this study is to present an
algorithm to resolve an optimization issue in a system consisting of orders
placed across multiple enterprises and undergoing several production
procedures. This algorithm is founded on formulating a general optimization
problem and utilizing established mathematical optimization techniques for
production planning. The presented method is oriented to
problem-solving in the universal case of multistage production, which
substantiates the theoretical significance of the study: most of the studied
heuristic algorithms (Halim, Hidayat, and
Aribowo, 2021; Paramita, Karimah, and Yatmo, 2021; Maulidya et al., 2020) are adapted at the moment to solve specific planning
problems.
2.1. Research objective
In general, there are two subtypes of optimization
tasks in production systems with multiple sequential processing operations:
1. In the first instance, the system's constraint is
known; this paper does not address it because its definition is linked to the
techniques of the theory of constraints (Kiran, 2019). In this case, it is essential to consider loading
the system constraint as much as possible.
2. In the latter instance, the constraint is
uncertain, and thus, it is crucial to consider the potential for its discovery
when addressing the issue at hand.
Thus, in the general case, the
problem is formally stated as follows: a specific set of orders N (in
this scenario, referred to as the "order", which is the entity that
passes through the production process from input to output) needs to be
optimally assigned to M productions based on a criterion, such as (1).
is a set of
completion dates for the production processes of the set of N orders.
The element of the set is the
completion date of a particular order.
The problem is typically framed as a single-criterion
optimization problem. Additionally, other optimization criteria can be
introduced, such as maximizing the number of products completed by a given
deadline or optimizing the workload of a specific enterprise within the M
set. These criteria can either replace or supplement the original criterion to
form a multi-criteria optimization task.
The production process comprises P separate
procedures that must be executed in a strict sequence. The procedures and their
execution sequence remain identical, regardless of the enterprise. In general,
transitions between enterprises are not allowed (i.e., it is impossible to
perform pi procedure at one enterprise and p i+1
procedure at another one).
Each enterprise in the M set is characterized
by a set of R resources having a capacity equal to P. Each
enterprise resource is linked one-to-one to the procedure performed at this
enterprise.
For each N set order, an S set is
created containing the essential resources to perform the procedures with a
corresponding P-capacity. Each element in this set is linked one-to-one
to the procedure performed for this order.
For each order, an L set is also established to
determine the duration of the procedures (the capacity of the set is P).
Based on the elements of this set, the objective function max is calculated.
If the system has a known constraint, system (2) takes the form (3):
is the procedure that is restrictive in
nature, assuming a standardized implementation across all enterprises; any deviations from this
standard require adjustments to the system (3).
It is permitted to switch
from system (3) to system (2) even in the case of a known system constraint to
achieve a quasi-optimal state since it is not always possible to achieve full
loading of the constraint. The duration of operations (and the ensuing change
in resource requirements) cannot typically be changed to meet the system (3)
requirements.
2.2. Existing solutions
In
order to formulate the optimization problem in practice and select the optimal
equation, the entire production process is taken into account collectively, and
each of its sections (procedures) is considered separately (Guseinov, Kurbanov, and Melikov, 2014).
The
methods of production process algorithmization are one of the tools for
formalizing the system, which enables proceeding to a series of much smaller
local subtasks with reference to the overall goal of system optimization. The
process algorithmization requires identifying critical actions that are
essential to the overall production process, as well as structuring and
decomposing processes, defining required operations, and establishing their
relationships with one another (Zhuravleva and Sakovich, 2023; Karimov, 2021).
The
algorithm developed under this method for the production process must include a
clear sequence of actions and a list of all resources utilized at each stage to
ensure the attainment of specified production targets. In developing algorithms
for multi-stage processes, the following steps can be distinguished (Dolganov and Zuev, 2015):
1.
Technology analysis, decomposition of multi-stage processes, determination of
the purpose of each subprocess, its sequence, relationship, and place in
achieving the overall goal of the system;
2.
Determination of the required resources, encompassing details concerning their
characteristics such as the capacity of production sites, equipment
accessibility, constraints in processing applications, and additional pertinent
factors.
3.
Calculation of the size of production sites in relation to the types of
products manufactured;
4.
Analysis of applications accepted for processing, estimated duration of
production (based on historical data on completed projects, resource
employment, etc.), required resources, and appropriate production sites;
5.
Calculation of the personnel performing basic technological operations.
The
system is described as a set of production units (divisions, product processing
operations) that are primarily used to analyze resources and their consumption.
The chain links are interconnected by technological dependencies on the work
complexity and the amount of output (Danilov, Ryzhova, and Voinova,
2010).
Shipbuilding
industry optimization can be considered an example of resolving this issue.
Such production sites assemble several product units at the same time. When
drawing up a production plan, it is challenging to create groups of products
from the current order portfolio that are then best assembled simultaneously in
the designated order at the company's assembly sites while also taking into
account the lowest achievable assembly-related costs (Sidorenko
and Khobotov, 2009).
In
addition, similar issues can be resolved using information modeling (Lebedeva and Sompol’tseva, 2020). The product information model is the basis for
building an automated production management system. Designing databases that
contain technological data, including information on necessary equipment and
tools, regulatory and technical documentation, and the procedure for
technological operations, is essential for building information models. Product
information models are used to determine the timing, planning, and need for the
purchase of materials. Possible production scenarios are also generated based
on the manufactured structure's information model, taking into account the
available production capacities (Lebedeva and Sompol’tseva,
2020). It is advisable to use
information models of products when creating a production plan to calculate the
required resource costs and allocate production areas based on orders. It is
possible to identify the optimal strategy for loading the enterprise by comparing
data on the specifics of the applications that were received with the current
utilization of resources.
Additionally,
it is suggested that automated production preparation systems for the
shipbuilding industry be introduced. These systems would be based on the
division of the hull into blocks and sections and the method chosen for forming
the hull on the slipway. A typical technological process of ship assembly is
selected for the incoming application on the basis of databases on common
sections and blocks (Surkov, 2005).
The
analysis of the sources thus reveals that the existing solutions are specific
and are applied to particular production conditions or optimization
functions. An example of such a
solution is a batch scheduling model for a three-stage hybrid Flowshop
producing products with a hierarchical assembly structure, applicable to a
hierarchical shop floor production structure (Maulidya et al., 2020). A similar example is the
development of an algorithm that has as its basis an optimization function for
minimizing the total production time (Halim, Hidayat, and
Aribowo, 2021). A separate area of
research is algorithms for collective production and cooperation (Paramita, Karimah,
and Yatmo, 2021), which are not considered
in this paper due to their inappropriateness to the task at hand. In this
regard, the
creation of
a single
versatile algorithm
might be
of utmost
importance. It also confirms the need for additional
algorithmization so that formal methods of task assignment and optimal
scheduling are applied adaptively, taking into account the specifics of a
particular task.
The suggested algorithm handles two variations of
the general problem (with a known or unknown constraint) by adapting to the
conditions. In the case of a known constraint, the optimization model is a
two-level one: at the first level, scenarios are generated based on the
intention to maximize the load of the constraint procedure; at the second
level, the scenarios are refined to form an integral production program. When
the constraint is unknown, a quasi-optimal scenario is formed through
sequential local optimization. This approach minimizes the complexity of the
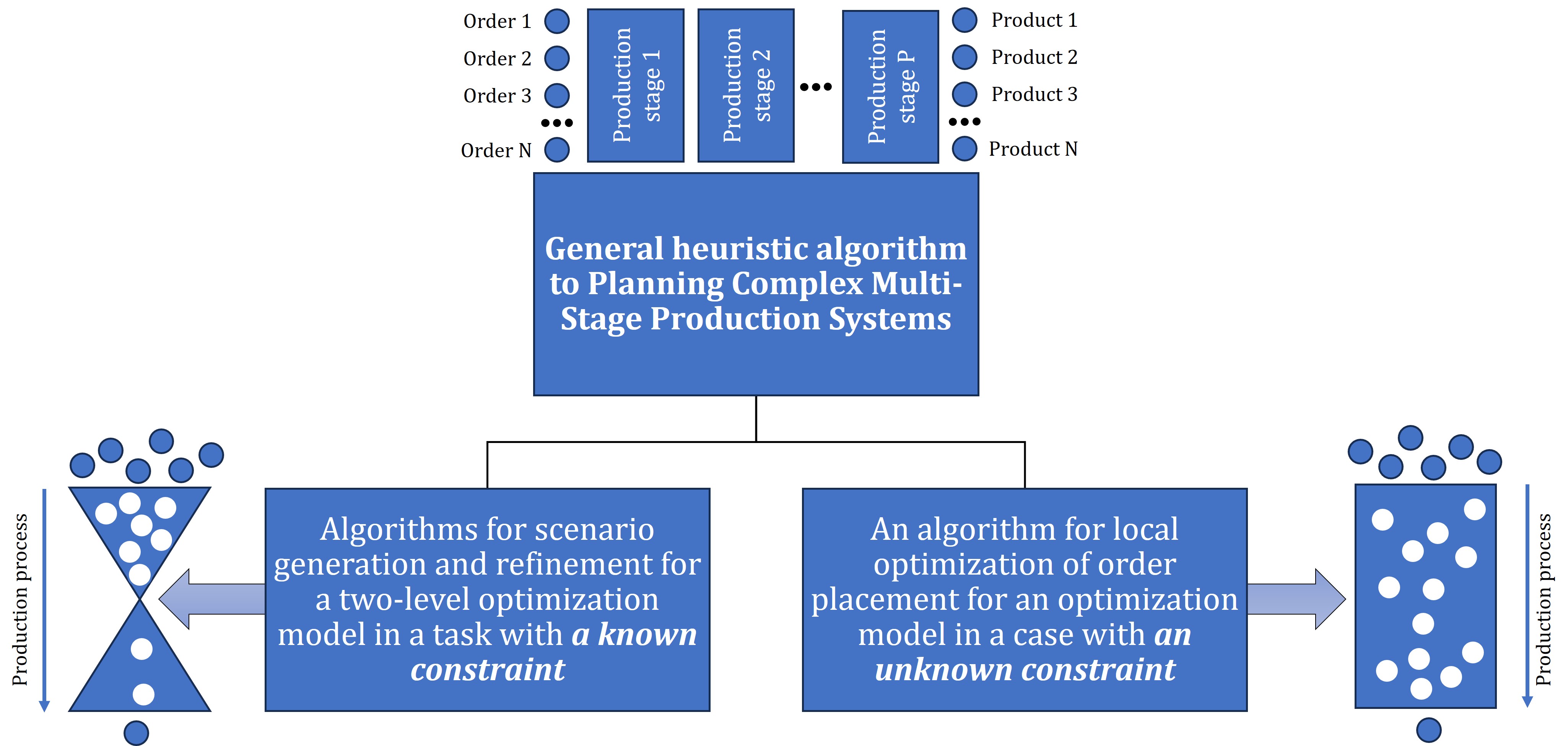
algorithm implementation. Figure 1 shows the algorithm in broad strokes.
Figure
1 General algorithm for
resolving the optimization issue
A two-level algorithm implies the following
steps:
1. Make a list of potential order assignment
scenarios for enterprises including variations in the processing order and the
method used to select a production site for each order. At this point, only the
constraint procedure – the system's bottleneck – is taken into account.
2. Rank scenarios for assigning performers in
ascending order of the calculated penalty function. When an order is not
fulfilled (not included in the scenario), the penalty is assigned. The penalty
function can also consider the order priority if there is an order
prioritization system. The use of the penalty function is a well-known
technique for finding quasi-optimal states within production planning tasks (Laha and Gupta, 2016).
3. Calculate the schedule for all procedures of
the first few scenarios with the lowest values of the penalty function. At the
same stage, the value of the penalty function's value should be updated subject
to the calculated performer schedules by work groups. It is likely that when
considering scenarios, the penalty functions will change, and the scenario that
was suboptimal at the upper level will become optimal. To achieve this, some
scenarios are refined.
4. Select the best scenario based on the penalty
function recalculation results.
Figure 2 shows the algorithms for the
subprocesses of scenario generation and refinement for a two-level optimization
algorithm.
Figure
2 Algorithms for scenario
generation and refinement for a two-level optimization model in a task with a
known constraint
Let us focus on the areas where it is possible to
specify and improve the two-level algorithm. The penalty function may consider
additional factors (such as the workload of enterprises, the geographic
distance between the business and the customer, etc.) when finalizing and
supplementing data. In addition, the order processing procedure and the
principle of assigning an enterprise to it can both be decided randomly and
based on calculations of the production site’s loads, specializations for
certain orders, etc.
When a
constraint is unknown, a heuristic algorithm for finding a global optimum
through local optimization of order placement is adopted. In order to solve
these issues, heuristic algorithms are used (Ongcunaruk
and Ongcunaruk, 2021; Utama et
al., 2019), since
this enables obtaining a satisfactory result in the absence of sufficient data
and the impossibility of their accurate processing. Low data quality appears
likely when taking into account the complexity of the model system under
consideration.
A
quasi-optimal scenario for the order production in this situation is achieved
by generating many different scenarios, both by chance and by some empirical
dependence (it is allowed to arrange the processing sequence in ascending or
descending order of some order characteristics, for instance, planned labor
intensity). The optimization criterion may also take the form of a penalty
function akin to the description provided for the two-level branch of the
algorithm.
Figure 3 An algorithm for local optimization of order placement
for an optimization model in a case with an unknown constraint
Turning to the discussion,
we highlight the main features of the algorithm, including its limitations, and
describe its primary application areas. We conclude the discussion by noting
the main alternative methods for addressing the presented problems.
It
should be noted that the algorithm in the second variation, based on local
optimization, performs well for production with a long cycle and a small number
of products. In the case of a large number of products, the complexity of the
greedy algorithm increases significantly, which leads to a nonlinear increase
in computational time. For this reason, the approach is recommended for heavy
industry, shipbuilding, aircraft manufacturing, and other productions with a
long cycle. At the same time, prior
research indicates that greedy algorithms for solving such problems are
applicable (Wang et al., 2023).
The
proposed method is focused on the universal case of multi-stage production,
taking into account the principles of the Theory of Constraints, which is an
extension and addition to the existing base of methods. Nevertheless, it also has a number of limitations.
In particular, it implies a fundamental difficulty in determining the
approximation of the quasi-optimal solution to the global optimum, which is a
separate future research problem that has not yet been solved in this paper.
Another limitation is the applicability of the algorithm to production with a
long cycle and a small number of products, which was mentioned above.
The
algorithm has undergone testing for optimization issues in a heavy industry
enterprise. The results obtained enable the creation of sets of scenarios close
to optimal with satisfactory computational time.
In
network tasks, a range of optimization methods can be employed to improve
efficiency. These include adapted methods for solving assignment problems,
workshop tasks, and the branch-and-bound method.
Based
on the results of the formulation of the production process optimization
problem, an algorithm is suggested that can be applied to both problems with
known constraints and problems with unknown constraints. The algorithm is
focused on quasi-optimization, which limits the effectiveness of its
application to the degree of approximation to the globally optimal result. At
the same time, it is not possible to reliably assess this degree at the current
stage - the development of available methods for such determination is the
topic of further research. This particular model for solving production
planning issues is appropriate for heavy industry enterprises characterized by
parallel and long-term manufacturing of high-tech complex products. According
to the analytical review, most planning tasks in such systems are resolved
using original techniques. In certain instances, tasks are accomplished using
empirical patterns, and the production plan is developed manually. Automating
the creation of quasi-optimal scenarios within this industry can prove highly
beneficial and efficient, serving as a valuable tool for generating production
program scenarios and as a component of decision support systems. The algorithm
was tested on the task of compiling a medium-term (5-10 years) production
schedule for a heavy industry enterprise. The main limitation in its practical application,
except for the above-mentioned limitation of approaching the global optimum, is
the speed of computation, which increases strongly with the increase of both
production objects and producing subjects or procedures. In this regard, a
further research task is to speed up the computation both at the level of the
algorithm and in practical program implementation. If this task is solved, it
will be possible to talk about the possibility of applying the algorithm in a
wider range of tasks, including mass production tasks.
The
research is funded by the Ministry of Science and Higher Education of the
Russian Federation (contract No. 075-03-2023-004 dated 13.01.2023).
Bengio, Y., Lodi, A.,
Prouvost, A., 2021. Machine Learning for
Combinatorial Optimization: A Methodological Tour D’horizon. European Journal of Operational Research, Volume 290(2), pp. 405–421
Costas, J., Puche, J., Ponte, B., Gupta, M. C., 2023. An Agent-Based Simulator for Quantifying the Cost of Uncertainty in Production
Systems. Simulation Modelling Practice and Theory, Volume 123, p. 102660
Danilov, G.V., Ryzhova, I.G., Voinova, E.S., 2010. Analysis and Optimization of the Enterprise's
Production Capacity Structure. Scientific and Technical News of the
St. Petersburg State Polytechnic University. Economic Sciences, Volume
4(102), pp. 87–90
Dolganov, K.B., Zuev, V.A., 2015. Features of Creating
a Distribution Center Simulation Model. IMMOD, Volume 2015, pp. 110–114
Guseinov, I.A., Kurbanov, Z.G., Melikov, E.A., 2014. Control of Non-Stationary Multi-Stage Processes in the
Petrochemical Industry. News of the Russian Academy of Sciences. Theory and
Control Systems. Volume 4, p. 90
Halim, A.H., Hidayat, N.P.A., Aribowo, W., 2021. Single Item
Batch-scheduling Model for a Flow Shop with m Batch-processing Machines to
Minimize Total Actual Flow Time. International Journal of Technology, Volume 13(4), pp. 816–826
Karimov, J.H., 2021. Procedures for Optimizing Global Goals of a Multistage Process Control System. Universum Technical Sciences, Volume 11–1 (92), pp. 48–52
Kiran, D.R., 2019.
Chapter 28 - Theory of Constraints. Production Planning and Control. Butterworth-Heinemann
Laha, D., Gupta,
J.N.D., 2016. A Hungarian Penalty-Based Construction Algorithm to
Minimize Makespan and Total Flow Time in No-Wait Flow Shops. Computers &
Industrial Engineering, Volume 98, pp. 373–383
Lebedeva E.G., Sompol’tseva, A.A., 2020. Analysis of the Development of
Technological Processes in the Manufacture of Ship Structures. Marine Smart Technologies, Volume 4-1, pp. 61–68
Lee, J., Kim, B.,
Kim, S.H., 2023. A Matheuristic Algorithm for Block Assignment
Problem in Long-Term Production Planning in the Shipbuilding Industry. Computers &
Industrial Engineering, Volume 184, p. 109603
Li, Y., Qi, X., 2020.
A Geometric Branch-And-Bound Algorithm for the Service Bundle Design Problem. European
Journal of Operational Research, Volume 303(3), pp. 1044-1056
Maulidya, R.,
Suprayogi, Wangsaputra, R., Halim, A.H., 2020. A Batch Scheduling Model for a
Three-stage Hybrid Flowshop Producing Products with Hierarchical Assembly
Structures. International Journal of Technology, Volume 11(3), pp. 608–618
Ongcunaruk, W., Ongkunaruk, P., 2021. A Construction Heuristic for the
Bin-Packing Problem with Time Windows: A Case Study in Thailand. International
Journal of Technology. Volume 12(2), pp. 390–400
Paramita, K.D., Karimah, A., Yatmo, Y.A., 2021. Collective Strategies and Spatialities of Neighborhood
Food Coproduction during COVID-19 Pandemic. International Journal of
Technology. Volume 12(6), pp. 1228–1238
Sidorenko, A.M., Khobotov, E.N., 2009. Production Planning with Parallel
Assembly of Products. News
of the Moscow State Technical University Named After, Volume 3, pp. 100–109
Surkov, K.M., 2005. Automated Development of Technological Processes for Ship Hull Assembly. News of the Astrakhan
State Technical University, Volume 2, pp. 182–187
Utama, D.M., Widodo, D.S., Wicaksono, W., Ardiansyah, L.R., 2019. A New
Hybrid Metaheuristics Algorithm for Minimizing Energy Consumption in the Flow
Shop Scheduling Problem. International Journal of Technology.
Volume 10(2), pp. 320–331
Wang Y., Han Y., Wang Y., Li J., Gao K., Liu Y., 2023. An
Effective Two-Stage Iterated Greedy Algorithm for Distributed Flowshop Group
Scheduling Problem with Setup Time. Expert Systems with Applications, Volume 233, p. 120909
Yazdani, M.A.,
Khezri, A., Benyoucef, L., 2021. A Linear Multi-Objective Optimization Model
for Process and Production Planning Generation in a Sustainable Reconfigurable
Environment. IFAC-Papers OnLine, Volume 54 (1), pp.
689–695
Zakharenkov, K.V., Mrochek, Zh. A., Mrochek, T.V.,
2018. Algorithm for Solution of Multicriterion Problem of Production Planning of Pipes and Shaped Products. System Analysis and Applied Information Science, Volume 4 (9), pp. 4–10
Zhuravleva, N.A., Sakovich, O.I.,2023. Algorithmization of Production
Processes in Freight Rail Service Sales. News of the Scientific Research
Results, Volume 1, pp.
114–124
Zukhruf, F., Frazila, R.B., Widhiarso, W., 2020. A Comparative Study on
Swarm-based Algorithms to Solve the Stochastic Optimization Problem in
Container Terminal Design. International Journal of Technology, Volume 11(2), pp. 374–387
