Revolutionizing Signature Recognition: A Contactless Method with Convolutional Recurrent Neural Networks
Corresponding email: whkhoh@mmu.edu.my
Published at : 10 Jul 2024
Volume : IJtech
Vol 15, No 4 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i4.6744
Chuen , A.L.F., How, K.W., Han, P.Y., Yen, Y.H., 2024. Revolutionizing Signature Recognition: A Contactless Method with Convolutional Recurrent Neural Networks. International Journal of Technology. Volume 15(4), pp. 1102-1117
| Alvin Lim Fang Chuen | Faculty of Information Science & Technology, Multimedia University, Jalan Ayer Keroh Lama, Bukit Beruang, 75450, Melaka, Malaysia |
| Khoh Wee How | Faculty of Information Science & Technology, Multimedia University, Jalan Ayer Keroh Lama, Bukit Beruang, 75450, Melaka, Malaysia |
| Pang Ying Han | Faculty of Information Science & Technology, Multimedia University, Jalan Ayer Keroh Lama, Bukit Beruang, 75450, Melaka, Malaysia |
| Yap Hui Yen | Faculty of Information Science & Technology, Multimedia University, Jalan Ayer Keroh Lama, Bukit Beruang, 75450, Melaka, Malaysia |
Conventional contact-based hand signature
recognition methods are raising hygienic concerns due to shared acquisition
devices among the public. Therefore, this research aimed to propose a
contactless in-air hand gesture signature (iHGS) recognition method using
convolutional recurrent neural networks (C-RNN). Experiments have been
conducted to identify the most suitable CNN architecture for the integration of
CNN and RNN. A total of four base architectures were adopted and evaluated,
namely MS-CNN-A, MS-CNN-B, CNN-A, and CNN-B. Based on the results, CNN-A was
selected as the convolutional layer for constructing the integration of C-RNN
due to its superior performance, achieving an accuracy rate of 95.15%.
Furthermore, three variants of C-RNN were proposed, and experimental results on
the iHGS database showed that the ConvBiLSTM achieved the highest accuracy at
98.10%, followed by ConvGRU at 97.47% and ConvLSTM at 97.40%.
Convolutional-RNN; Gesture recognition; Hand gesture signatures; In-air signatures
Hand signature is a handwritten
name or initials that are typically used for identity verification and
authentication purposes in legal documents, banking and finance transactions,
employment agreements, and government services (Hashim, Ahmed,
and Alkhayyat, 2022). Due to its
uniqueness, two individuals sharing the same name will show distinct hand
signature. This is due to individual behavioral traits such as pressure applied
to the writing surface, speed, and the angle of handling the writing instrument
(Impedovo and Pirlo, 2007).
These factors will influence the overall appearance and style of signature,
which contribute to its uniqueness. The practicality and widespread use of hand
signature has made it to become one of the most commonly applied forms of
behavioral biometrics. However, the traditional method for recognition is
through manual checking by humans, which is susceptible to error during the
identification of the signature (Akram, Qasim, and Amin, 2012).
The advancement of technology has led to the
introduction of automatic hand signature recognition systems, which have
mitigated the risk of human error in the identification of hand signatures (Faundez-Zanuy, 2005).
Generally, there are two types of hand signature recognition systems, namely
offline and online (Julian and Ortega-Garcia, 2008; Gilperez et al., 2008). The offline method only
captures the appearance and shape by scanning the hand signature. Meanwhile,
the online method captures other dynamic properties such as pressure applied to
the writing surface and signature completion time. This system can be further
classified into contact-based and contactless methods (Jain et al., 2020; Malik et al., 2018).
The contact-based method captures the hand signature using a pen and paper, as
well as the latest method, which uses a stylus and tablet technology. The
contactless method does not require direct contact with acquisition devices by
in-air signing in front of a camera sensor.
The contact-based method that
uses pen and paper is vulnerable to forgery issues as individuals need to
physically write their signature, exposing the shape and allowing imitation by
others for unauthorized uses. Although the stylus and tablet method can address
this issue by capturing dynamic properties, it is still a contact-based
susceptible to germ and virus contamination as the acquisition devices are
often shared among the public. Recently, the occurrence of the COVID-19 global
pandemic has increased concerns about hygiene related to contact-based
biometrics recognition systems, leading to high demands for contactless systems (Gan, 2022; Romadlon,
Lestiana, and Putri, 2022; Supriatna et
al., 2022; Yatmo, Harahap,
and Atmodiwirjo, 2021; Carlaw, 2020). Contactless hand signature
recognition methods are already in existence (Khoh et al., 2021; Fang et al., 2017; Sajid and Cheung,
2015), but their applications in currently in the experimental
stage. According to previous research, commercially available systems still
rely on contact-based methods for applications such as identity verification in
financial institutions (Sudharshan and
Vismaya, 2022; Karanjkar and Vasambekar, 2016; Cuceloglu and Ogul, 2014).
Shao et al., (2020), Levy et al., (2018) proposed
hand gesture-based signature recognition method using built-in sensors from
mobile devices. Subjects perform in-air signatures when wearing a smartwatch or
holding a smartphone to capture the gestures. However, this method only
captures the device's coordinates over time, lacking spatial information on
hand. Azlin
et al. (2022) proposed a
hand gesture-based recognition method using a camera sensor to capture
signature. The method mainly focuses on compressing entire image sequences into
a single image for recognition, without providing temporal information.
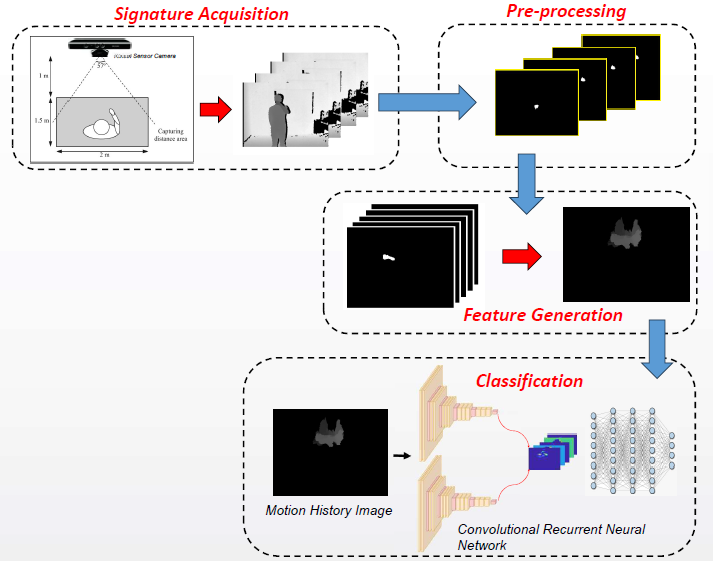
The
database and pre-processing methods were initially introduced in this section,
followed by a detailed explanation of proposed CNN and integrated C-RNN.
2.1. In-air hand Gestures Signatures Database (iHGS)
This database comprised a total of 2980 samples, including 2000 genuine and 980 forged samples. Hand gesture signature acquisition was carried out in a controlled environment, using a Microsoft Kinect sensor that captured both color and depth images. The sensor was pre-set to operate at a resolution of 640 x 480 and 30 frames per second. Furthermore, 100 individuals who participated in database collection were instructed to stand one meter away from the sensor and position their hand in front, activating the standby mode, before performing hand gesture signature. Each individual contributed 20 samples of genuine signature. For the collection of forged samples, participants were given a sufficient amount of time to learn and replicate the signature of other individuals. The acquisition of forged signature started after the participants showed readiness, with Figure 1 showing a sample of the depth image.
Figure 1
Depth image frame of a subject writing a signature in the air with their hand.
2.2. Pre-processing
In this research, only the depth image
sequences of in-air hand gestures were used to evaluate the performance of the
proposed methods. After segmenting the palm area, 2D and 3D features were
generated. Specifically, 2D features store only spatial information, which is
used to train the base CNN. 3D features store both spatial and temporal
information, which are designated for training the integrated C-RNN.
2.2.1. Palm Detection and Segmentation
Although CNN is designed to learn and
extract features without the need for handcrafted feature extraction
algorithms, the process still requires a large number of training samples to
obtain optimal performance. Due to the scarcity of hand gesture signature
samples, the background noises were removed to prevent the models from
misinterpretation. The entire palm area is preserved and considered as the
region of interest (ROI) of a particular sample.
The palm detection is initially performed using the thresholding method to remove the noise. A threshold value is set to 180, according to the outcome of the empirical tests to obtain the most optimum setting. Any pixel value in the image sequences below this threshold value is set to 0, corresponding to the pixel value of the black color. Although the palm region serves as the closest object to the sensor at the beginning of hand gesture signature motions, there are no restrictions on how the subjects can perform hand gesture. This phenomenon leads to the detection of both the palm and face regions. For instance, when subjects move their hand to the far left or right, both the face and palm regions become the closest objects to the sensor. Figure 2 shows instances where both regions are segmented together in the same frame. To address this issue, the predictive palm segmentation algorithm proposed by (Khoh, Pang, and Teoh, 2019) is applied, using the detected palm location in the first frame as a reference to predict the closest palm point in other frames. Figure 3 shows that only the palm region remains in the frame after applying the predictive palm segmentation.
Figure 2 Incorrect segmentation where both the face and palm region are captured
Figure 3
Correct segmentation where only the palm region is captured after applying the
predictive palm segmentation algorithm
2.2.2. Feature Generation
In the feature generation stage, both 2D
and 3D imagery features are generated from the segmented image sequences. The
Motion History Image (MHI), proposed by (Davis and Bobick, 1997) is used for generating features for both 2D and 3D
hand gesture signature features. Moreover, the MHI is a static image that
condenses spatio-temporal information from a sequence of frames into a single
image (Sincan and Keles, 2022; Lakshmi and Devendran,
2021; Ahad et al., 2012). In the generation of 2D
features, in-air hand gesture signature – Motion History Image (iHGS-MHI) is
used as the designated notation. The silhouettes of palm motion from the
segmented image sequences are compressed into a single static image. Figure 4
shows the process of generating iHGS-MHI features, where MHI is produced from
the segmented image sequences.
The
segmented image sequences are already in a 3D format which can be fed into the
recurrent neural network (RNN). However, the method is not computationally
efficient due to the need to identify the largest frame in the samples and
apply zero-padding to standardize the number of depths for each hand gesture
signature. This phenomenon is capable of causing an increase in computational
resources as the model's input dimension needs to match the largest sample's
frame numbers. The zero-padding method can also cause the model to consider the
padded frames as part of the features due to the variation in the number of
frames across the hand gesture signature samples. For instance, some samples
can have fewer than 50 frames, while others are above 100 frames. To address
this issue, a more computationally efficient method for 3D feature generation
is introduced to reduce the number of padding frames.
The depth for each sample is standardized to 10 blocks, containing 10 frames. In the initial stage of 3D feature generation, hand gesture samples of fewer than 100 frames are categorized as small, while those exceeding 100 frames are categorized as large. The segmented image sequences are partitioned into 10 blocks and MHI is generated from each block, compressing 10 frames into a single image, as shown in Figure 5. In comparison, the 10th block of small samples is an empty block filled using the zero-padding method, while large samples contain more than 10 frames, ranging from frame number 91 to the end of the sequence. Figure 6 shows a scenario featuring one sample with 43 frames and another with 183 frames. The small samples have sufficient frames only to the 4th block and the remaining are padded with zeros, while the large samples exceed 100 frames. The 10th block stores frame numbers 91 to 183, and the MHI appears larger compared to the previous 9 blocks due to the compression of more frames. Compared to the previous blocks, the 10th block in a large sample captures more than 10 frames.
Figure 4 Feature generation of iHGS-MHI
Figure 5 Feature generation of iHGS-MHI-BLOCKS
Figure 6
Illustration of HGS-MHI-BLOCKS on small and large samples
2.3. Proposed architecture
In this section, the architecture of
both CNN and RNN are presented, along with the integration method to build
C-RNN.
2.3.1. Convolutional Neural Networks (CNN)
In this research, two variants of CNN are
proposed, namely multiscale Convolutional Neural Networks (MS-CNN) which
extract and learn features at multiple scales simultaneously, and the base CNN
operating at a single scale. Each variant has the same number of layers. The
first layer of the models is a convolution layer with a kernel size of 3x3 and
32 filters. The second layer also has a kernel size of 3x3 but with 64 filters.
Meanwhile, the main difference between both models is at the third and fourth
layers. In MS-CNN, these layers consist of parallel convolution layers with 3x3
and 5x5 kernels, each having 64 filters to extract features at different
scales. The feature maps from both convolutional layers are concatenated,
resulting in a total of 128 filters. The third and fourth layers of the base
CNN consist of convolutional layers with 128 filters each. Figure 7 shows the
difference between parallel and typical single-scale convolution layers.
Figure 7
Comparison of parallel and typical convolution layers
The outputs of each convolutional layer are
activated using the Rectified Linear Unit (ReLu) function. Max pooling is
applied at the end before the feature maps are passed to other layers for
further feature extraction and dimension reduction. The final layers of these
models consist of fully connected (FC) layers, which learn and map the features
extracted by the previous convolutional layers. Moreover, the first FC layer
consists of 1024 neurons, where 50% are dropped before passing to the final
layer using the dropout regularisation method. This layer contains 100 neurons,
corresponding to the total number of classes. Subsequently, the Softmax
function is applied for classification purposes, which computes the output of
the final FC layer into a probability distribution with values ranging from 0
to 1, and the sum of all classes equal to 1.
Both
MS-CNN and CNN have two variants, which are with and without batch
normalization. Specifically, batch normalization is a regularization method
that is used to accelerate training time and improve model accuracy. This
improvement is achieved by reducing the internal covariate shift, which is the
change in the distribution of inputs to each layer during the training process (Bjorck et al., 2018; Kohler et al.,
2018; Santurkar et al., 2018; Ioffe and Szegedy, 2015). Table 1 presents the
detailed information for each architecture.
Table 1
Proposed CNN Architectures
2.3.2. Recurrent Neural Networks (RNN)
RNN is mainly designed for learning time
series or sequential data. It can store and learn from sequential data due to
the presence of recurrent connections. However, the base RNN often encounters
vanishing gradient issues when dealing with long-sequence data. This limitation
occurs due to the lack of a gating mechanism that can selectively store,
update, or remove information. Hochreiter and Schmidhuber (1997) proposed the Long Short-Term
Memory (LSTM) architecture to address the limitation of the base RNN.
The LSTM architecture is comprised of four main
components, namely memory cells, input, output, and forget gates. The core
component is the memory cell, which is responsible for maintaining the internal
state of the unit. The input gate manages and decides the amount of new
information from the current input to be stored in the memory cell. The output
gate is responsible for deciding which information should be passed to
subsequent units and stored in the hidden state. Meanwhile, forget gate decides
which information should be stored and removed. Another variant of LSTM, known
as bidirectional LSTM, has also been proposed by Graves and Schmidhuber (2005).
This variant is a stacked LSTM that receives inputs from both the forward and
backward directions, with a similar internal structure as the base LSTM.
A more
recent variant of RNN is the Gated Recurrent Unit (GRU), proposed by Cho et al.
(2014), which has fewer parameters and uses only two gating
mechanisms. In this variant, the update gate decides which information should
be kept or removed from the candidate state, serving as a temporary memory
space where new information is stored. Meanwhile, the reset gate determines the
amount of past information to be removed from the hidden state. Table 2 summarises
the information on all RNN architecture variants.
Table 2 RNN Architectures Information
|
Architecture |
States |
Gating
Mechanism |
Sequence
Direction |
|
Base
RNN |
Hidden
State |
- |
Unidirectional |
|
LSTM |
Hidden
State, Cell State |
Input,
Output, Forget |
Unidirectional |
|
Bidirectional
LSTM |
Hidden
State, Cell State |
Input,
Output, Forget |
Bidirectional |
|
GRU |
Hidden
State, Candidate State |
Update,
Reset |
Unidirectional |
2.3.3. Convolutional Recurrent Neural Networks (C-RNN)
An integrated architecture is introduced that combines convolutional layers for spatial feature extraction with RNN for temporal feature learning. The sequence folding and unfolding layers developed by MathWorks (2022) are used to construct this integrated architecture. A sequence folding layer is added after the input layer, followed by convolutional layers, which are used to extract features from each frame from the image sequences. Subsequently, a sequence unfolding layer is added and convolutional features extracted from the image sequences are flattened and fed into the RNN layers for temporal feature learning. The outputs from the RNN layers are passed to a fully connected layer, where the Softmax function is applied for classification. Figure 8 shows the complete workflow of C-RNN, while the detailed information regarding the architectures is presented in Table 3. The three proposed variants of C-RNN include Convolutional Long Short-Term Memory (ConvLSTM), Convolutional Bidirectional Long Short-Term Memory (ConvBiLSTM), and Convolutional Gated Recurrent Unit (ConvGRU).
Figure 8
Convolutional Recurrent Neural Network workflow
Table 3 Proposed C-RNN Architectures
|
Layer |
ConvLSTM |
ConvBiLSTM |
ConvGRU |
|
1 |
Input
224 x 224 x 10 |
Input
224 x 224 x 10 |
Input
224 x 224 x 10 |
|
2 |
Sequence
Folding |
Sequence Folding |
Sequence Folding |
|
3 |
Convolutional
Layers |
Convolutional
Layers |
Convolutional
Layers |
|
4 |
Sequence
Unfolding, Flatten |
Sequence
Folding, Flatten |
Sequence
Folding, Flatten |
|
5 |
Long
Short-Term Memory Dropout:
0.2 |
Bidirectional
Long Short-Term Memory Dropout: 0.2 |
Gated
Recurrent Unit Dropout: 0.2 |
|
6 |
FC
Layer: 100 Softmax |
FC
Layer: 100 Softmax |
FC
Layer: 100 Softmax |
2.4. Experimental Setup
In this
section, the implementation environments, the initial training of CNN variants,
and the experiment with C-RNN are explained in detail.
2.4.1. Hardware
and Software Configuration
The
experiments were conducted in Matlab R2021a on a desktop computer running
Windows 11 64-bit operating system. The computer is equipped with an Intel
i5-12400f CPU, a base clock speed of 2.5 GHz, 16GB of RAM, and an Nvidia RTX
3060 GPU with 12GB of VRAM and 3584 CUDA cores.
2.4.2. Training Hyperparameters
All the models are trained with a
learning rate of 0.001, 20 epochs, and a mini-batch size of 32 using the
Stochastic Gradient Descent with momentum (SGDM) optimizer. Moreover, the
training process started from scratch five times, with the dataset divided into
an 80:20 ratio. During each trial, 80% of the samples were randomly selected
for training and 20% for testing purposes. Table 4 summarizes the training
hyperparameters used in this research.
Table 4
Training Hyperparameter
|
Epoch |
Batch
Size |
Learning
Rate |
Train-Test
Ratio |
Optimizer |
|
20 |
32 |
0.001 |
80:20 |
SGDM |
2.5. Experiment
Setting
2.5.1. Experiment on CNN
The
four proposed variants of CNN architectures, including MS-CNN-A, MS-CNN-B,
CNN-A, and CNN-B, are initially trained on the 2D features, namely HGS-MHI. The
architecture with the highest accuracy and the least amount of training time is
selected as the convolutional layer foundation for constructing the C-RNN.
2.5.2. Experiment on C-RNN
The CNN architecture that obtained the
optimal performance from the first experiment is selected to construct the
integrated architecture of C-RNN. The number of hidden units in the RNN serves
as the main hyperparameter value. Experiments are carried out with hidden units
of 128, 256, and 512 to identify the optimal value that obtains the highest
recognition accuracy with minimal computation time. Table 5 shows the
experimental setting for both CNN and C-RNN.
Table 5
Experimental Setting
|
Architecture |
Input
Dimension |
Training
Features |
Hidden
Units (RNN) |
|
CNN |
224x224x1 |
iHGS-MHI |
- |
|
C-RNN |
224x224x10 |
iHGS-MHI-BLOCKS |
128,
256, 512 |
2.6. Evaluation Measurement
The evaluation metrics of accuracy, precision, specificity, recall, and F1-score are used to evaluate the performance of the proposed architectures. Equation 1 describes the calculation of accuracy, which is obtained by dividing the sum of True Positives (TP) and True Negatives (TN) by the total number of test data instances. This serves as the sum of True Positives (TP), True Negatives (TN), False Negatives (FN), and False Positives (FP), measuring the ratio of correctly predicted observations to the total observations. Equation 2 defines precision as the ratio of TP to the sum of TP and FP, measuring the proportion of TP predictions out of all positive predictions made. Meanwhile, Equation 3 defines specificity as the ratio of TN to the sum of TN and FP, which measures the proportion of actual negatives that are correctly identified. Equation 4 defines recall as the ratio of TP to the sum of TP and FN, measuring the proportion of actual positives that are correctly identified. Equation 5 defines the F1-score, which is a weighted average of precision and recall. The measurements are described as follows:
In this
section, the experimental results of averaged classification accuracy and model
training computation time are analyzed and discussed in detail.
3.1. CNN
Experimental Results
This section discusses the experimental
results of four base variants of CNN to identify optimal convolutional layers
for constructing the integrated architectures of C-RNN. As shown in Table 6,
the experimental results for both variants of CNN and MS-CNN. MS-CNN-A achieved
an accuracy of 95.05%, requiring 1 minute and 56 seconds for computation.
MS-CNN-B recorded an accuracy of 93.90%, showing the need for only 1 minute and
35 seconds to train. Although batch normalization is generally used as a
regularization method to enhance model accuracy and minimize training time, the
first MS-CNN variant with batch normalization consumed more computation time by
21 seconds. Meanwhile, batch normalization also helped to increase the model
accuracy by 1.15%.
Table 6
Performance Comparison of MS-CNN and CNN
|
Architecture |
Classification measurement (Averaged ± SD) | |||||
|
|
Accuracy |
Precision
|
Specificity |
Recall |
F1-Score |
Train
Time |
|
MS-CNN-A |
95.05
± 0.86 |
96.13
± 0.59 |
99.95
± 0.01 |
95.25
± 0.88 |
94.90
± 0.84 |
1
min 56 sec |
|
MS-CNN-B |
93.90
± 0.58 |
95.10
± 0.45 |
99.94
± 0.01 |
93.90
± 0.58 |
93.76
± 0.63 |
1
min 35 sec |
|
CNN-A |
95.15
± 0.95 |
96.07
± 0.82 |
99.95
± 0.01 |
95.15
± 0.95 |
94.96
± 1.00 |
1
min 42 sec |
|
CNN-B |
94.50
± 1.13 |
95.67
± 0.94 |
99.94
± 0.01 |
94.50
± 1.13 |
94.30
± 1.23 |
1
min 27 sec |
The
MS-CNN variants are expected to have better performance compared to CNN, due to
the presence of parallel convolution layers extracting features at different
scales simultaneously. However, both variants of CNN outperform the MS-CNN,
achieving an accuracy of 95.15%, which is 0.10% higher than MS-CNN-A. CNN-B
obtained an accuracy of 94.50%, which is 0.65% lower than the first variant,
requiring a training time of 1 minute and 27 seconds. This significant
difference is attributed to the lack of batch normalization, as observed in the
MS-CNN results.
Figures 9 and 10 show the classification accuracy and computation time for all variants of MS-CNN and CNN. These initial experiments are carried out to identify the model with the highest recognition accuracy and the least amount of computational time, resulting in the selection of CNN-A as the convolutional layer for constructing C-RNN. Although CNN-B is the fastest model, requiring the least amount of computation time to train, it is underperformed in terms of accuracy. Both variants of MS-CNN also obtained lower accuracy, leading to the selection of CNN-A as the best architecture, considering that all proposed architectures had training times within the range of 1 minute.
Figure 9 Accuracy comparison of MS-CNN and CNN
Figure 10
Computation time comparison of MS-CNN and CNN
3.2. C-RNN Experimental Results
CNN-A with the highest recognition
accuracy from the preliminary experiments is selected as the base for
convolutional layers in the integrated architecture of C-RNN. The experimental
results for three C-RNN variants show a different number of hidden units of
128, 256, and 512, respectively. The optimal value for the hidden units is
explored and analyzed to identify the architecture with the highest accuracy
with minimal computation time.
All three variants of the C-RNN achieved
greater accuracy compared to CNN architectures, as shown in Table 7. The
average computation time also increased from 1 minute to 3 minutes, which was
expected as the model complexity rose with the integration of both CNN and RNN
architectures. The ConvLSTM, ConvBiLSTM, and ConvGRU models achieved accuracy
of 97.20%, 97.40%, and 97.10%, respectively. Regarding computation time,
ConvLSTM lasted for 3 minutes and 21 seconds to train, while ConvBiLSTM which
used stacked LSTM layers to receive inputs from both forward and backward
directions, was expected to require significantly more time. According to
experimental results, 3 minutes and 54 seconds were required for training,
which was only 33 seconds more than the previous LSTM model. The fastest model
among the three variants was ConvGRU, which requires 3 minutes and 10 seconds
to train. This result is obtained due to the fewer parameters of the internal
structure of GRU compared to LSTM, thereby requiring less computation time.
Table 7
Average Classification Result (%) on 128 Hidden Units
|
Architecture |
Classification measurement (Averaged ± SD) | |||||
|
|
Accuracy |
Precision |
Specificity |
Recall |
F1-Score |
Train Time |
|
ConvLSTM |
97.20 ± 0.82 |
97.75 ± 0.70 |
99.97 ± 0.01 |
97.20 ± 0.82 |
97.13 ± 0.88 |
3 min 21 sec |
|
ConvBiLSTM |
97.40 ± 1.26 |
98.00 ± 0.91 |
99.97 ± 0.01 |
97.40 ± 1.26 |
97.33 ± 1.30 |
3 min 54 sec |
|
ConvGRU |
97.10 ± 1.02 |
97.70 ± 0.81 |
99.97 ± 0.01 |
97.10 ± 1.02 |
97.02 ± 1.06 |
3 min 10 sec |
Table
8 shows a significant rise in average training time, as the number of hidden
units increases from 128 to 512. Based on the results, the computation time for
ConvLSTM and ConvGRU increases by 32 seconds and 27 seconds, respectively.
ConvBiLSTM shows the most significant increase in training time, rising from 3
minutes and 10 seconds to 4 minutes and 56 seconds, due to the bidirectional
nature. Although the number of hidden units is set to 256, a total of 512
hidden units is used, where 256 are allocated for the forward pass and 256 for
the backward pass. As the computational time increases significantly, there is
only a minor improvement in accuracy. The ConvLSTM, ConvBiLSTM, and ConvGRU
also show accuracy increase of 0.20%, 0.07%, and 0.30%, respectively.
Table 8 Average Classification Result
(%) on 256 Hidden Units
|
Architecture |
Classification measurement (Averaged ± SD) | |||||
|
|
Accuracy |
Precision |
Specificity |
Recall |
F1-Score |
Train Time |
|
ConvLSTM |
97.40 ± 0.68 |
97.88 ± 0.63 |
99.97 ± 0.01 |
97.40 ± 0.68 |
97.36 ± 0.73 |
3 min 53 sec |
|
ConvBiLSTM |
97.47 ± 1.32 |
97.98 ± 1.01 |
99.97 ± 0.01 |
97.47 ± 1.32 |
97.40 ± 1.34 |
4 min 56 sec |
|
ConvGRU |
97.40 ± 0.98 |
97.90 ± 0.80 |
99.97 ± 0.01 |
97.40 ± 0.98 |
97.33 ± 0.97 |
3 min 37 sec |
In
Table 9, as the number of hidden units increased from 256 to 512, ConvLSTM accuracy
remained the same compared to the previous experiment with 256 units. However,
the average training time increased from 3 minutes and 53 seconds to 5 minutes
and 3 seconds, showing that a high number of hidden units does not benefit
ConvLSTM. ConvGRU showed a modest accuracy increase of 0.05%, requiring an
additional 1 minute and 4 seconds to train. The ConvBiLSTM showed the highest
observed improvement in accuracy, with the number of hidden units increasing to
512, showing a 0.63% high as the average accuracy rises from 97.47% to 98.10%.
This improvement was attributed to the increased training time, which
facilitated the slowest architecture among the C-RNN variants.
Table 9
Average Classification Result (%) on 512 Hidden Units
|
Architecture |
Classification measurement (Averaged ± SD) | |||||
|
|
Accuracy |
Precision |
Specificity |
Recall |
F1-Score |
Train Time |
|
ConvLSTM |
97.40 ± 0.84 |
97.93 ± 0.74 |
99.97 ± 0.01 |
97.40 ± 0.84 |
97.36 ± 0.85 |
5 min 03 sec |
|
ConvBiLSTM |
98.10 ± 0.86 |
98.48 ± 0.70 |
99.98 ± 0.01 |
98.10 ± 0.86 |
98.07 ± 0.88 |
7 min 27 sec |
|
ConvGRU |
97.45 ± 1.08 |
97.93 ± 0.93 |
99.97 ± 0.01 |
97.45 ± 1.08 |
97.38 ± 1.12 |
4 min 33 sec |
Figure
11 shows an accuracy comparison of all C-RNN variants. Based on the results,
ConvBiLSTM with 512 hidden units is the only architecture to achieve the
highest accuracy of 98.10%, while other variants range from 97.10% to 97.47%.
As shown in Figure 12, average training
time also rises with the increase in the number of hidden units. The
architectures with 128, 256, and 512 hidden units fall within an accuracy range
of 97%, except for ConvBiLSTM with 512 hidden units. Furthermore, all
architectures with 128 hidden units are the most computationally efficient,
with an accuracy within the range of 97% and the least amount of training time.
Figure 11 Accuracy comparison of C-RNN
Figure 12
Computation time comparison of C-RNN
In conclusion, this research successfully
proposed the use of C-RNN for in-air hand gesture signature (iHGS) recognition,
introducing four base CNN architectures. The results showed that MS-CNN-A and
MS-CNN-B captured and extracted features at different scales parallelly while
the CNN-A and CNN-B were operated at a single scale. CNN-A was selected as the
convolutional layer foundation for the integrated architecture, with the
highest accuracy of 95.15%. Subsequently, three additional architectures were
proposed, namely ConvLSTM, ConvBiLSTM, and ConvGRU. The
experimental results showed a significant increase in recognition accuracy by
minimizing the loss of information, preserving in a 3D representation, and
feeding into the C-RNN models. However, this improvement was obtained due to
increased computation time caused by the architectural integration, with the
ConvBiLSTM obtaining the highest accuracy of 98.10%, while ConvLSTM and ConvGRU
achieved 97.40% and 97.47%, respectively. The average training duration
increased from 1 minute to 3 minutes because of the architectural integration
in the initial C-RNN experiments with 128 hidden units due to the increased
complexity. The training time further increased to 4, 5, and 7 minutes, as the
hidden units rose to 256 and 512. The optimal hyperparameter value was 128
hidden units for all variants of C-RNN, with an accuracy of 97% and an average
training time of 3 minutes. However, only minor accuracy improvement was
observed from 128 to 256 and 512, along with higher computational time.
The authors are grateful to the Ministry of Higher
Education (MOHE) for funding under the Fundamental Research Grant Scheme (FRGS)
(FRGS/1/2021/ICT02/MMU/03/3).
Ahad, M.A.R., Tan,
J.K., Kim, H., Ishikawa, S., 2012. Motion History Image: Its Variants and
Applications. Machine Vision and Applications, Volume 23, pp. 255–281
Akram, M., Qasim, R., Amin, M.A., 2012. A Comparative Study
of Signature Recognition Problem Using Statistical Features and Artificial
Neural Networks. In: 2012 International Conference on Informatics,
Electronics & Vision (ICIEV), pp. 925–929
Azlin, A.I.A.b., Han, P.Y., How, K.W., Yin, O.S., 2022. Hand
Gesture Signature Recognition with Machine Learning Algorithms. In: International
Conference on Computational Science and Technology, pp. 389-398
Bjorck, N., Gomes, C.P., Selman, B., Weinberger, K.Q., 2018.
Understanding Batch Normalization. Advances in Neural Information Processing
Systems, Volume 31, pp. 1–12
Carlaw, S., 2020. Impact on Biometrics of Covid-19. Biometric
Technology Today. Volume 2020(4), pp. 8–9
Cho, K., Merrienboer, B.V., Gulcehre, C., Bahdanau, D.,
Bougares, F., Schwenk, H., Bengio, Y., 2014. Learning Phrase Representations
using RNN Encoder–Decoder for Statistical Machine Translation. In: Proceedings
of the 2014 Conference on Empirical Methods in Natural Language Processing
(EMNLP), pp. 1724–1734
Cuceloglu, ?., Ogul, H., 2014. Detecting Handwritten
Signatures in Scanned Documents Detecting Handwritten Signatures in Scanned
Documents. In: Proceedings of the 19th Computer Vision Winter
Workshop, Volume 2014, pp. 89–94
Davis, J.C., Bobick, A.F., 1997. The Representation and
Recognition of Human Movement Using Temporal Templates. In: Proceedings
of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,
pp. 928–934
Fang, Y., Kang, W., Wu, Q., Tang, L., 2017. A Novel
Video-Based System for in-Air Signature Verification. Computers & Electrical Engineering.
Volume 57, pp. 1–14
Faundez-Zanuy, M., 2005. Signature Recognition
State-of-The-Art. IEEE Aerospace and Electronic Systems Magazine, Volume
20 (7), pp. 28–32
Gan, K.B., 2022. FACE SHIELD@UKM: An Initiative by UKM To
Protect Our Frontliner During Covid-19 Pandemic. International Journal on
Robotics, Automation and Sciences, Volume 4, pp. 30–34
Gilperez, A., Alonso-Fernandez, F., Pecharroman, S., Fierrez,
J., Ortega-Garcia, J., 2008. Off-line Signature Verification Using Contour
Features. In: 11th
International Conference on Frontiers in Handwriting Recognition, pp. 1–6
Graves, A., Schmidhuber, J., 2005. Framewise Phoneme
Classification with Bidirectional LSTM Networks. In: Proceedings 2005
IEEE International Joint Conference on Neural Networks, Volume 4, pp. 2047–2052
Hashim, Z., Ahmed, H.M., Alkhayyat, A.H., 2022. A Comparative
Study among Handwritten Signature Verification Methods Using Machine Learning
Techniques. Scientific Programming. Volume 1, p. 8170424
Hochreiter, S., Schmidhuber, J., 1997. Long Short-Term
Memory. Neural Computation, Volume 9(8), pp. 1735–1780
Impedovo, S., Pirlo, G., 2007. Verification of Handwritten
Signatures: an Overview. In:14th International Conference on
Image Analysis and Processing (ICIAP), pp. 191–196
Ioffe, S., Szegedy, C., 2015. Batch Normalization:
Accelerating Deep Network Training by Reducing Internal Covariate Shift. International
Conference on Machine Learning, pp. 448–456
Jain, A., Singh, S.K., Singh, K.P., 2020. Handwritten
Signature Verification Using Shallow Convolutional Neural Network. Multimedia
Tools and Applications, Volume 79, pp. 19993–20018
Julian, J., Ortega-Garcia, J., 2008. On-Line Signature
Verification. Handbook of Biometrics, pp. 189–209
Karanjkar, S.L., Vasambekar, P.N., 2016. Signature
Recognition on Bank Cheques Using ANN. In: IEEE International WIE
Conference on Electrical and Computer Engineering (WIECON-ECE), pp. 44–47
Khoh, W.H., Pang, Y.H. Yap, H.Y., 2022. In-air Hand Gesture
Signature Recognition: An iHGS Database Acquisition Protocol. F1000Research,
Volume 11, p. 283
Khoh, W.H., Pang, Y.H., Teoh, A.B.J., 2019. In-air Hand
Gesture Signature Recognition System Based on 3-Dimensional Imagery. Multimedia
Tools and Applications, Volume 78(6), pp. 6913–6937
Khoh, W.H., Pang, Y.H., Teoh, A.B.J., Ooi, S.Y., 2021. In-air
Hand Gesture Signature Using Transfer Learning and Its Forgery Attack. Applied
Soft Computing, Volume 113, p. 108033
Kohler, J., Daneshmand, H., Lucchi, A., Zhou, M., Neymeyr,
K., Hofmann, T., 2018. Towards A Theoretical Understanding of Batch
Normalization. Stat, Volume 2018, pp. 1–33
Lakshmi, K., Devendran, T., 2021. Human Fall Detection Using
Motion History Image and SVM. In: Advanced Informatics for Computing
Research: 4th International Conference, ICAICR 2020, Gurugram, India, December
26–27, 2020, Revised Selected Papers, Part I 4, pp. 466–476
Levy, A., Nassi, B., Elovici, Y.,
Shmueli, E., 2018. Handwritten Signature
Verification Using Wrist-Worn Devices. In: Proceedings of the ACM on
Interactive, Mobile, Wearable and Ubiquitous Technologies, Volume 2(3), pp.
1–26
Malik, J., Elhayek, A., Ahmed, S., Shafait, F., Malik, M.,
Stricker, D., 2018. 3DAirSig: A Framework for Enabling In-Air Signatures Using
a Multi-Modal Depth Sensor. Sensors, Volume 18(11), p. 3872
MathWorks, 2022. Classify Videos Using Deep Learning - MATLAB
& Simulink. Available online at:
https://www.mathworks.com/help/deeplearning/ug/classify-videos-using-deep-learning.html,
Accessed on July 17, 2022
Romadlon, F., Lestiana, F., Putri, N.A.,
2022. An Exploration of Personal Decision as
Mediating Effect between Passenger Concern and Airport Service Information
During COVID-19 Outbreak. International Journal of Technology, Volume
13(3), pp. 664–676
Sajid, H., Cheung, S., 2015. VSig: Hand-Gestured Signature
Recognition and Authentication with Wearable Camera. International Workshop
on Information Forensics and Security (WIFS), pp. 1–6
Santurkar, S., Tsipras, D., Ilyas, A., Madry, A., 2018. How
Does Batch Normalization Help Optimization. In: Advances in Neural
Information Processing Systems, Volume 31, pp. 1–11
Shao, Y., Yang, T., Wang, H., Ma, J.,
2020. AirSign: Smartphone Authentication by Signing in the Air. Sensors, Volume
21(1), p. 104
Sincan, O.M., Keles, H.Y., 2022. Using
Motion History Images with 3D Convolutional Networks in Isolated Sign Language
Recognition. IEEE Access, Volume 10, pp. 18608–18618
Sudharshan, D.P., Vismaya, R.N., 2022.
Handwritten Signature Verification System using Deep Learning. In:
International Conference on Data Science and Information System (ICDSIS), pp.
1–5
Supriatna, Zulkarnain, F., Ardiansyah,
Rizqihandari, N., Semedi, J.M., Indratmoko, S., Rahatiningtyas, N.S.,
Nurlambang, T., Dimyati, M., 2022. Communicating the High Susceptible Zone of
COVID-19 and its Exposure to Population Number through a Web-GIS Dashboard for
Indonesia Cases. International Journal of Technology, Volume 13(4), pp.
706–716
Yatmo, Y.A., Harahap, M.M.Y.,
Atmodiwirjo, P., 2021. Modular Isolation Units for Patients with
Mild-to-Moderate Conditions in Response to Hospital Surges Resulting from the
COVID-19 Pandemic. International Journal of Technology, Volume 12(1),
pp. 43–53
