Machine Learning Algorithms for Failure Prediction Model and Operational Reliability of Onshore Gas Transmission Pipelines
Corresponding email: andy.noorsaman@ui.ac.id
Published at : 09 May 2023
Volume : IJtech
Vol 14, No 3 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i3.6287
Noorsaman, A., Amrializzia, D., Zulfikri, H., Revitasari, R., Isambert, A., 2023. Machine Learning Algorithms for Failure Prediction Model and Operational Reliability of Onshore Gas Transmission Pipelines. International Journal of Technology. Volume 14(3), pp. 680-689
| Andy Noorsaman | Department of Chemical Engineering, Faculty of Engineering, Universitas Indonesia, Depok 16424, Indonesia |
| Dea Amrializzia | Department of Process Engineering, PT. Rekayasa Engineering, Jl. Kalibata Timur II No.36, South Jakarta, Jakarat 12740, Indonesia |
| Habiburrahman Zulfikri | Department of Chemical Engineering, Faculty of Engineering, Universitas Indonesia, Depok 16424, Indonesia |
| Reviana Revitasari | Department of Chemical Engineering, Faculty of Engineering, Universitas Indonesia, Depok 16424, Indonesia |
| Arsene Isambert | Laboratoire de Genie de Procedes et Materiaux, Ecole Centrale Paris, F 92295 Chatenay Malabry Cedex, France |
A
transmission pipeline is the safest and most effective way of transporting
large volumes of natural gas over long distances. However, if not maintained
efficiently, failures of gas transmission pipelines can occur and cause
catastrophic events. Therefore, an accurate prediction of pipe failures and
operational reliability is required to determine the optimal pipe replacement timing
such that the incidence of pipe failures can be prevented. Nowadays,
computer-assisted technology helps businesses make better decisions, and
machine learning is among the excellent techniques that can be utilized in
predicting failures. In this study, two machine learning algorithms, i.e.,
random forest and binary logistic regression, are developed, and their
prediction abilities are compared. The model is developed based on a decade of
unstructured and complex historical failure data of the onshore gas
transmission pipelines released by the United States Department of
Transportation. The modeling process begins with data pre-processing followed
by model training, model testing, performance measuring, and failure
predicting. Both algorithms have demonstrated excellent
results. The random forest model achieved an AUC of 0.89 and a predictive
accuracy of 0.913, while the binary logistic regression model outperformed with
an AUC of 0.94 and a prediction accuracy of 0.949. The trained model is further
employed to predict future failures on a 11900-mile natural gas pipeline
spanning from Louisiana to the northeast section of the United States. We show
the location of the pipes that will be broken in the interval of five years and
estimate that 29%/63%/83% of the pipes will break by 2025/2030/2035.
Binary logistic regression; Failure prediction; Machine learning; Random forest; Transmission pipeline
Natural gas as a petroleum substitute offers many economic, technological, and environmental benefits and increases efficiency because it is quickly developed (Lee et al., 2012) as cited in Bawono and Kusrini, 2017). It is a versatile energy source because it can be stored and transported in trucks or tankers as liquified natural gas, medium-conditioned liquified gas, or compressed natural gas (Ríos-Mercado and Borraz-Sánchez, 2015) as cited in (Farizal, Dachyar, and Prasetya, 2021). However, Mikolajková-Alifov et al. (2019) study conveys that transporting large amounts of natural gas via pipelines, one of which is through onshore gas transmission pipelines, is more cost-effective (Farizal, Dachyar, and Prasetya, 2021). A submarine pipeline in a submerged floating tunnel (SFT) is proposed as an alternative solution to pipeline-related ecological issues (Budiman, Raka, and Wahyuni, 2017). However, SFT is not covered by the scope of this study, which is concerned with a natural gas pipeline that runs from Louisiana to the northeast United States.
Although
more efficient than trucks or tankers, onshore gas transmission pipelines face
serious challenges. Its failures are disastrous, causing financial losses,
environmental damage, and even death. Gas pipeline failures are caused by
several factors, including pipe/weld material failure, excavation damage,
corrosion, equipment failure, soil movement, and incorrect operation (Dai et al., 2017). Between January 2010 and November
2017, approximately 17.55 billion cubic feet of methane gas was lost through
the transmission pipeline in the United States. This amount of gas is enough to
heat around 233 thousand houses for a year. Unfortunately, during this period,
pipeline failures caused nearly 100 fatalities, and around 500 injuries, and
incurred a cost of approximately 1.1 billion US dollars
In the
context of industrial internet of things (IIoT)– increased interconnectedness
and opportunities to collect data, process and analyze information – predictive
maintenance can be a good strategy to face the problem. Predictive maintenance
utilizes a wealth of process data and advanced analytical methods to predict
failures well before urgent action has to be taken.
The current
era of the fourth industrial revolution has enabled computer-assisted
technology to help businesses, including the oil and gas industries, make
better decisions (Hanga and
Kovalchuk, 2019).
In particular, machine learning techniques, which allow for automation of the
process of analytical model building, offer great potential in predicting
failures accurately. Machine learning tools are built to learn from data by
establishing data structures and mapping complex relationships between input
parameters and targets such that they can adapt to future input data (Shalev-Shawrtz and Ben-David, 2014). For instance, recently, the
machine-learning created model for predicting pipe failures in water supply
networks in Seville, Spain, shows detailed estimation and suggest specific and
realistic suggestion to prevent approximately 30% of failures by replacing only
3% of the network's pipes annually (Robles-Velasco et al., 2020). Eastvedt, Naterer, and Duan
(2022) have
presented a method of monitoring a subsea oil pipeline for fault detection
using a regression-supervised machine learning (ML) algorithm. ML algorithms
were developed by using flow velocity data derived from ANSYS Fluent
simulations, pressure, and temperature. It shows that the ML algorithm could
97% accurately predict the outputs (Eastvedt, Naterer,
and Duan, 2022). A study has also been carried out by
analyzing the performance of the Bayesian network in predicting pipe failure
using a large and highly variable dataset from the water distribution system in
the United Kingdom. Method one involved a supervised learning method to build a
Bayesian network by understanding common failure types (joint, pinhole,
circumferential, and longitudinal), while method two involved an automated
learning method. The Bayesian network built using the automated method was able
to achieve an overall accuracy of 84.4% compare to the 81.2% for the Bayesian
network supervised learning method (Tang, Parsons,
and Jude, 2019). Therefore, machine learning, if trained properly, can predict
failures quickly and accurately. In this study, two ML algorithms, i.e., random
forest and binary logistic regression, are developed, and their performances
are compared in predicting a decade of historical data on gas transmission
pipeline failures in the US.
2.1. Raw Dataset
Figure 1 Map of status of pipes for onshore natural gas transmission in the United
States from 2010 to 2020
2.2. Methods
Pre-processing,
learning, testing, performance measuring, and mapping of the datasets were
performed using R, a language and software environment for statistical
computing, version 4.0.2. R studio version 1.2.5042 was used as an integrated
development environment for R. The ‘caret’ R package was used to perform the
models (Kuhn, 2008), and Leaflet, an
open-source JavaScript library, is employed to create an interactive map of the
pipes network with the attached state of failure.
2.2.1. Data Pre-Processing
Raw datasets
are usually not used directly in machine learning because of several reasons,
including missing values and noises. Therefore, data pre-processing is
necessary to perform easy operations in later steps. Firstly, the attributes
deemed irrelevant to the prediction system, such as gas flow, and the
attributes with more than 50% missing values, are eliminated. Secondly, to
improve the predictors’ predictive performance and to simplify the model for
easy interpretation, several most influential attributes in the prediction
problems are selected based on the importance value (Guyon
and
Elisseeff, 2003). Here, calculations of filter-based variable importance were
carried out to select attributes for the model. Thirdly, we divided the dataset
into 90% of the dataset for the training set and the remaining 10% for the
testing set. We note that the percentage of failed and not-failed pipes in both
training and testing data sets is the same.
It is well
known that the problem of learning from imbalanced data (He and
Gracia, 2009) emerged from underrepresented data, and severe class distribution
skews can cause the standard classification models to perform improperly (Wang et al., 2013). In the
present study, the dataset is imbalanced as 84% of the data are correlated to
the “fail” status, and hence the model will tend to predict a “fail” status.
One method that can be applied to solve the imbalance problem, which is
employed in the present study, is the Randomly Over Sampling Example (ROSE)
technique. One method that can be applied to solve the imbalance problem, which
is employed in the present study, is the Randomly Over Sampling Example (ROSE)
technique (Lunardon, Menardi, and Torelli, 2014). After
incorporating the imbalanced treatment is incorporated in the pre-processing
step, the user data is ready to be used for the machine learning algorithms.
2.2.2. Failure Prediction
Modeling: Training and Testing
The random forest algorithm is a classification
model that consists of a structured collection of trees. Unlike a decision
tree, which only consists of one tree in the classification and prediction
process, a random forest creates a voting mechanism for the class, which
significantly affects the accuracy of the model (Chen, Liaw, and Breiman, 2004). Decision trees are generated using the
attribute selection indicators such as information acquisition, acquisition
ratio, and the Gini index for each attribute. The Gini index is used to measure
the probability of a particular variable being misclassified when randomly
selected.
where
f(x) is the predicted output. n is the number of decision trees in the
forest.
fi(x) is the predicted output of the ith decision tree.
Each decision tree is trained on a different subset of the training data
and a random subset of the features. The final prediction is made by taking the
average of the predictions of all the decision trees.
Random forest depends on
a random vector value with the same distribution in all trees. Each decision
tree has the maximum depth. The random forest is a classifier consisting of a
tree classifier is a random vector distributed independently,
and each tree with the most votes and the most popular class is selected as a
result. RF is arguably simpler and more powerful than other non-linear
classification algorithms (Breiman, 2001).
2.2.3. Measuring Performance
In building
the prediction system, we need a numerical indicator to tell whether the system
performs well or not. The performance is measured by the confusion matrix, the
receiver operating characteristic (ROC) curve, and the estimation of the
accuracy. The confusion matrix contains the real values against those predicted
for the validation set (Table II). There are four possible results for each
sample: true-positive (TP), true-negative (TN), false-positive (FP), and false-negative
(FN). Each box would include the value of observations of each type (Han, Kamber and Pei, 2000).
Table 1 Confusion matrix for
evaluating the performance of a classification model
|
|
|
Predicted |
| |
|
|
|
Negative |
Positive | |
|
Actual |
Negative |
TN |
FP | |
|
Positive |
FN |
TP | ||
The Receiver
Operating Characteristics curve depicts the TP rate (or recall) against the FN
rate (or 1?specificity) for the different values of a risk threshold. The
accuracy is calculated as the fraction of the correct predictions to the total
predictions. Furthermore, it is common to calculate the Area Under the Curve
(AUC) as a metric, representing a classifier’s ability to avoid false
classifications. The AUC is between 0 and 1
After
optimizing and testing the performance of the model, we applied it to predict
the failure on a 11900-mile natural gas pipeline that spans from Louisiana to
the northeast section of the United States. The pipeline is operated by the
Tennessee Gas Pipeline Company. The reconstructed dataset consists of
approximately 50 documented properties, including diameter, material, and
length.
We considered thirteen attributes, the importance value of which are
calculated and shown in Table II. The correlation value between pipe failures
(dependent variable) and other selected attributes (independent variable) from
the training datasets is listed in the column of Table II. Attributes, the
importance value of which is below 0.5, are considered to have no relevance to
pipe failures (Wang et al., 2016).
Therefore, the attributes "Explode Indication," "Ignite
Indication," and "Case" are excluded in the modeling stage, and
further computation will only consider the remaining ten attributes.
Table 2 Attributes of the
dataset with the type of data, description, and the important values between
each attribute and the “Failure” attribute.
|
Name
of Attributes |
Type |
Description |
Value |
|
Explode
Indication |
Categorical |
Indication
of possible pipe explosion |
0.206 |
|
Ignite
Indication |
Categorical |
Indication
of possible pipe ignition |
0.212 |
|
Cause |
Categorical |
Cause
of pipe failure |
0.215 |
|
MAOP |
Numerical |
Maximum Allowable Operating Pressure in
psig |
0.630 |
|
Thickness |
Numerical |
The
pipe’s wall thickness is in inch |
0.634 |
|
Depth |
Numerical |
The
depth of cover in inch |
0.637 |
|
Age |
Numerical |
The
pipe’s age in a year |
0.647 |
|
Area |
Categorical |
The
area of the laid pipe |
0.651 |
|
Coat |
Categorical |
The
pipe coating type |
0.655 |
|
Diameter |
Numerical |
The
nominal pipe size in inch |
0.689 |
|
Length |
Numerical |
The
length of isolation segment in ft |
0.741 |
|
Class |
Categorical |
The
pipe class (class 1, class 2, and class 3) |
0.842 |
|
Failure |
Categorical |
The
status of the pipe (fail or not fail) |
1 |
Table
3 displays how each algorithm performed on the testing data by creating the
confusion matrix for each algorithm. The rows in a confusion matrix correspond
to what the machine learning algorithm predicted, and the columns correspond to
the historical data. Both algorithms perform very well in predicting at least
93.5% of the failed pipes and 80% of the not-failed pipes. BLR algorithm
performs slightly better than the RF algorithm as BLR identifies 4 more failed
pipes correctly, bringing the percentage of correctly identified failed pipes
to 97.2%.
Table 3 Confusion matrix
obtained from the BLR and RF algorithms
|
Algorithm: BLR |
Predicted | ||
|
Not Fail |
Fail | ||
|
Actual |
Not Fail |
16 (80.0%) |
3 (2.8%) |
|
Fail |
4 (20.0%) |
104 (97.2%) | |
|
Algorithm: RF |
Predicted | ||
|
Not Fail |
Fail | ||
|
Actual |
Not Fail |
16 (80.0%) |
7 (6.5%) |
|
Fail |
4 (20.0%) |
100 (93.5%) | |
Table 4 presents a summary of the accuracy, sensitivity, precision, and F1 score of both studied algorithms. Based on the results, logistic regression is preferred over the random forest model due to its superior performance in terms of accuracy, precision, recall, and F1 score. The higher F1 score of the logistic regression model suggests that it is more effective in predicting outcomes and is more stable than the random forest model.
Table 4 The performance of machine learning algorithms
|
Performance |
Binary Logistic Regression |
Random Forest |
|
Accuracy |
0.945 |
0.913 |
|
Specificity |
0.842 |
0.696 |
|
Precision |
0.972 |
0.935 |
|
Recall |
0.963 |
0.962 |
|
F1
Score |
0.967 |
0.948 |
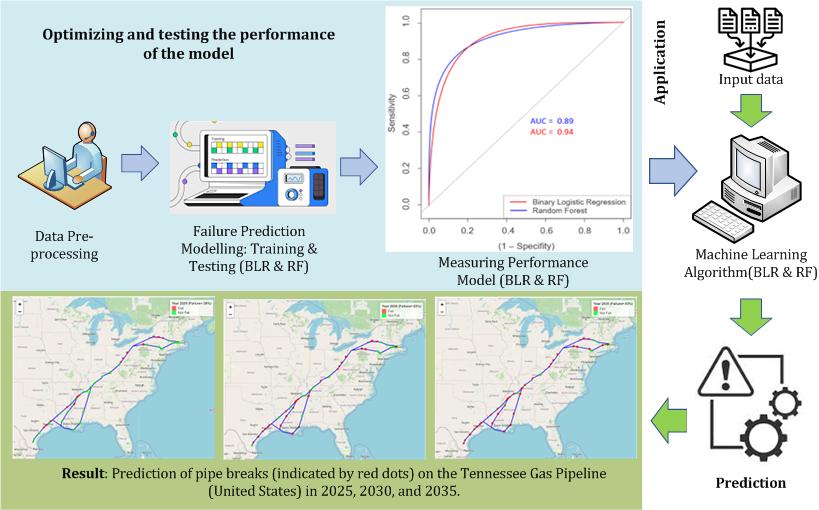
Figure 2 ROC curve for pipe failures obtained from the application of binary
logistic regression and random forest algorithms. The values of AUC are also
indicated.
ROC curves, which plot the true positive rate (sensitivity/recall) in the
y-axis as a function of the false positive rate (1?specificity) in the x-axis,
from the computations using each algorithm are shown in Figure 2. The ROC
curves for both methods can be categorized as excellent since the area under
the curve (AUC) value is higher than 0.9. (Hosmer and Lemeshow, 2000). Again, the BLR algorithm demonstrates a
slightly better performance as the resulting AUC is larger than that of RF
(0.89 vs 0.94).
As the binary logistic regression
algorithm shows better performance, we employ it to predict the failures of the
pipeline operated by the Tennessee Gas Pipeline. This pipeline is chosen
because the available data match the input attribute requirements of the
trained model. The results are mapped into the geographical location of the
pipeline shown in Figure 3. Our analysis
predicts that 29% of the pipes are expected to break by 2025, 63% by 2030, and 83%
by 2035. Interestingly, the percentage of predicted pipe breaks does not
increase monotonically as a function of time, with the highest number of pipe
breaks anticipated to occur between 2025 and 2030.
Figure 3 Prediction of pipe breaks (indicated by red dots) on the Tennessee Gas
Pipeline in 2025, 2030, and 2035
A study on the failure prediction and operational
reliability of gas transmission pipelines using random forest and binary
logistic regression algorithms has been carried out. Both algorithms showed
excellent results. Random forest has an AUC of 0.89 and a prediction accuracy
of 0.913, while the binary logistic regression shows better performance, namely
an AUC of 0.94 and a prediction accuracy of 0.949. The created model is
expected to help companies assess and predict failures of transmission gas
pipelines such that better inspections and maintenance schedules can be
conducted. The trained model predicts that 29%/63%/83% of the pipes on a
11900-mile natural gas pipeline spanning from Louisiana to the northeast
section of the United States will break by 2025/2030/2035. Several aspects can
be explored to further improve the present study. Firstly, we note that some
important attributes, e.g., temperature and natural gas flow, which we
estimate, can improve prediction performance, were not available in the raw
dataset. Secondly, this study has not considered the costs incurred due to pipe failures and the costs required
to maintain the pipes. Such economic analysis will be beneficial for the
industry to plan their annual budget accordingly. This study can help gas
transmission pipeline industry optimize their preventive maintenance schedule
in advance. This allows for estimating the remaining runtime of pipelines with
high accuracy. It also can estimate time to failure and identify which sections
of pipelines need to be fixed. By predicting failures before they happen,
companies can minimize the possibility of catasthrophic incidents, and the cost
due to unplanned downtimes or maintenance.
The authors would like to
thank the Process Systems Engineering Laboratory, Chemical Engineering
Department, Engineering Faculty, Universitas Indonesia for the computing
facilities provided.
Bawono, A. A., Kusrini, E., 2017. The Impacts
of Financing Investment
Scenarios On Piped-Natural Gas Prices (GPs) for Households in Indonesia. International
Journal of Technology, Volume 8(8), pp. 1402–1413
Breiman, L., 2001. Random Forest. Machine
Learning, Volume 45, pp. 5–32
Budiman, E., Raka, I., Wahyuni, E., 2017. Concept
Application for Pipelines Using A
Submerged Floating Tunnel for Use In The Oil and Gas Industry. International
Journal of Technology, Volume 8(4), pp. 719–727
Chen, C., Liaw, A., Breiman, L., 2004. Using Random
Forest to
Learn Imbalanced Data. Berkeley: Department of Statistics
Dai, L., Wang, D., Wang, T., Feng, Q., Yang, X., 2017. Analysis and
Comparison of Long-Distance
Pipeline Failures. Journal of Petroleum Engineering, p. 3174636
Eastvedt, D., Naterer, G., Duan, X., 2022. Detection of Faults
in Subsea Pipelines By
Flow Monitoring With Regression Supervised Machine Learning. Process Safety
and Environmental Protection, Volume 161(30), pp. 409–420
Farizal, Dachyar, M., Prasetya, Y., 2021. City Gas
Pipeline Routing Optimization Considering Cultural Heritage and Catastrophic Risk. International
Journal of Technology, Volume 12(5), pp. 1009–1018
Fawcett, T., 2006. An Introduction to ROC Analysis. Pattern
Recognition Letter, 27(8), pp. 861–874
Guyon, I., Elisseeff, A., 2003. An Introduction To Variable and Feature Selection. Journal
of Machine Learning Research, Volume 3, pp. 1157–1182
Han, J., Kamber, M., Pei, J., 2000. Classification:
Basic Concepts. Data mining: Concepts and Techniques. 3rd Edition. Burnaby: Morgan
Kaufmann Publishers
Hanga, K. M., Kovalchuk, Y., 2019. Machine Learning and Multi-Agent Systems in Oil and Gas Industry
Application : A Survey. Compter Science Review, Volume 34, p. 100191
Harrell, F. E., 2005. Binary Logistic Regression.
Regression Modeling Strategies. 2nd Edition. New York: Springer
He, H., Gracia, E. A., 2009. Learning from Imbalanced Data. Transactions
on Knowledge and Data Engineering, Volume 21(9), pp. 1263–1284
Hosmer, D. W., Lemeshow, S., 2000. Assessing
the Fit of The Model. In: Applied Logistic
Regression. 2nd Edition. New York City: John
Wiley & Sons
Kuhn, M., 2008. Building Predictive Models in R Using The Caret
Package. Journal of Statistical Software, Volume 28(5), pp. 1–26
Lee, A., Zinaman, O., Logan, J., Bazilian, M.,
Arent, D., Newmark, R. L., 2012. Interactions, Complementarities and Tensions at The Nexus of Natural Gas and Renewable Energy. The
Electricity Journal, Volume 25(10), pp. 38–48
Lunardon, N., Menardi, G. & Torelli, N., 2014.
ROSE: A Package For Binary Imbalanced Learning. R Journal, Volume 6(1), pp. 82–92
Mikolajková-Alifov, M., Petterson, F.,
Björklund-Sänkiaho, M., Saxén, H., 2019. Model Of Optimal Gas Supply To A
Set Of Distributed Consumers. Energies, Volume 12(3), pp. 1–27
Robles-Velasco, A., Cortes, P., Mun?uzuri, J., Onieva, L., 2020. Prediction of Pipe
Failures In Water Supply Networks Using Logistic Regression and Support Vector
Classification. Reliability Engineering & System Safety, Volume
196, p. 106754
Ríos-Mercado, R.Z., Borraz-Sánchez, C., 2015.
Optimization Problems In Natural Gas Transportation Systems: A State-Of-The-Art
Review. Applied Energy, Volume 147, pp. 536–555
Shalev-Shawrtz, Ben-David, S., 2014. Understanding Machine
Learning: From Theory To
Algorithms. New York: Cambridge University Press
Tang, K., Parsons, D. J., Jude, S., 2019. Comparison of Automatic
and Guided Learning For
Bayesian Networks to
Analyse Pipe Failures in The Water Distribution System. Reliability
Engineering & System Safety, Volume 186, pp. 24–36
Thompson, J., 2017. High Country News. Available Online at:https://www.hcn.org/issues/49.22/infographic-a-map-of-leaking-natural-gas-pipelines-across-the-nation, Accessed on June 10, 2020
Wang, G., Gunasekaran, A., Ngai, E.W.T., Papadopoulos, T., 2016.
Big Data Analytics In Logistics and Supply Chain Management: Certain investigations
for research and applications. International Journal of Production Economics,
Volume 176, pp. 98–110
Wang, R., Dong, W., Wang, Y., Tang, K., Yao, X., 2013. Pipe Failure Prediction: A Data Mining Method. In: IEEE 29th International Conference on Data Engineering (ICDE), pp. 1208–1218
