Joint User-Centric Clustering and Pilot Allocation for Scalable Cell-Free Massive MIMO System

Beyond 5G; Cooperative communications; Linear beamforming; Network-centric; Uniform rate

In cell-free massive multiple-input multiple-output (MIMO), all access points (APs) are cooperatively serving user equipments (UEs) in the network using the same time-frequency resources (Ngo et al., 2017; Marzetta, 2015; Larsson et al., 2014; Lu et al., 2014). A central processing unit (CPU) communicates with APs through front haul links. In the downlink, data symbols were transmitted from the CPU to all APs, while in the uplink, APs sent soft estimated symbols or forwarded all received signals to the CPU. The method used is dependent on whether the processing was performed in a distributed or centralized fashion, respectively. However, this original cell-free massive MIMO is not scalable because the computational complexity becomes infinite when the number of UEs increases (Femenias, Riera-Palou, and Björnson, 2023; Papazafeiropoulos et al., 2021; Bjornson and Sanguinetti, 2020; Interdonato, Frenger, and Larsson, 2019).

The user-centric cell-free massive MIMO introduced by Buzzi and D’Andrea (2017) is a practical method used to realize the benefits of coherent transmission. APs in the network MIMO context only served as a subset of UEs with the strongest channels (Xie et al., 2023; Alonzo and Buzzi 2017; Gesbert et al., 2010; Venkatesan, Lozano, and Valenzuela, 2007). It contrasts the network-centric method, where network densification generated more interference, especially for cell-edge UEs (Humadi et al., 2022; Buzzi et al., 2021). Consequently, the user-centric cell-free massive MIMO with distributed APs achieved better fairness and service uniformity among all UEs.

In cell-free massive MIMO, the number of UEs is typically much larger than the available orthogonal pilots, making it essential to associate UEs with APs and spectrum resources appropriately. The optimal joint design of APs selection and resource allocation included exhaustively searching all possible combinations of APs, UEs, and spectrum resources (Zeng et al., 2021; Teng et al., 2019; Liu and Lau, 2017). The optimal solution used to reduce the complexity and achieve scalable implementation, was to design a clustering algorithm, and then perform pilot allocation (Zhang, Yang, and Han, 2023; Ammar et al., 2022; Zhong, Zhu, and Lim, 2022).

Recent research on scalable cell-free massive MIMO systems focused on clustering and pilot allocation frameworks. These frameworks are generally divided into graph-based methods (Huang et al., 2023; Liu et al., 2020b; Hmida et al., 2020) and non-graph based methods (Wang et. al., 2021; Liu et al., 2020a; Bjornson and Sanguinetti, 2020; Sabbagh, Pan, and Wang, 2018). For graph-based frameworks, an interference graph is generated after associating UEs with APs. The available orthogonal pilots are then assigned to each cluster with the aim of minimizing the number of possible pilots used and consecutively allocating different colors to overlapping clusters. Assuming the number of pilots available is at least equal to the chromatic number of the graph, the performance of such a method is guaranteed (Chartrand and Zhang, 2019). This is because severe performance degradation due to pilot contamination is avoided. Hmida et al. (2020) developed an edge when two UEs are dominant interferes to each other in order to reduce the impact of pilot contamination. However, Liu et al. (2020b) proposed reducing the subset of APs serving UEs when the available pilots are insufficient to satisfy the chromatic number of the graph. This method tends to reduce spectral efficiency performance since fewer APs serve UEs. To address this issue, Huang et al. (2023) proposed the clustering of users connected to the same APs using the K-means algorithm, before allocating pilots based on a weighted contamination graph for inter-cluster users.

A non-graph based framework (Sabbagh, Pan, and Wang, 2018) assigns dynamic pilot for pilot-sharing UEs that are sufficiently separated to meet the signal-to-noise ratio (SINR) constraint. Liu et al. (2020a) adopted a Tabu-search based pilot allocation method aimed to maximize the sum spectral efficiency. Meanwhile, Wang et al. (2021) studied APs-UEs association based on large-scale fading decoding coefficients, optimized using the max-min SINR criteria, although the specific method for pilot allocation was not stated. Bjornson and Sanguinetti (2020) proposed a joint clustering and pilot allocation strategy, where each UE selects one master AP with the best channel among the surrounding APs. Additionally, the master AP assigns the pilot with the least contamination among the available options.

All the previous research contributed to the realization of a scalable cell-free massive MIMO system. However, it is of interest to compare the performance of graph- and non-graph based pilot allocation schemes when using a common clustering algorithm. Lin et al. (2018) proposed a Gale-Shapley user-centric clustering algorithm designed explicitly for ultra-dense network (UDN). This algorithm used the stable marriage criterion (Alruwaili, Kim, and Oluoch, 2024; Teo, Sethuraman, and Tan, 2001) to determine the association between APs and UEs based on respective preference lists. The stable clustering ensured no APs and UEs left unpaired that would prefer each other over current partners.

The proposed Gale-Shapley user-centric clustering algorithm (Lin et al., 2018) offered a polynomial complexity for pairing APs-UEs, contrasting the exponential complexity of optimal exhaustive pairing. Moreover, Lin et al. (2018) proved the stability of APs and UEs association, indicating no blocking pairs existed. It was also reported that the proposed Gale-Shapley based clustering provided superior network performance in terms of the sum and UE rates. Despite several research on user-centric clustering for cell-free massive MIMO, not one had focused on the Gale-Shapley method (Huang et al., 2023; Wang et al., 2021; Bjornson and Sanguinetti, 2020; Hmida et al., 2020; Liu et al., 2020a; 2020b; Sabbagh, Pan, and Wang, 2018).

Based on the low complexity and superior performance of Gale-Shapley clustering, this research proposed a joint user-centric clustering and pilot allocation for scalable cell-free massive MIMO systems. The aim was to provide uniform spectral efficiency for all UEs in the network, which led to the following specific contributions.

1.    The Gale-Shapley clustering (Lin et al., 2018) was combined with existing pilot allocation methods. This included the scalable (Bjornson and Sanguinetti, 2020) and graph-coloring methods (Liu et al., 2020b). The Gale-Shapley clustering (Lin et al., 2018) initially applied to UDN, considered the maximum number of UEs in APs as a constraint. In this research, the constraint is insignificant because the algorithm developed ensured that the number of serving UEs at each AP is equal to the available pilots.

2.  Numerical analysis was conducted on the cumulative distribution function (CDF) of spectral efficiency per UE of both pilot allocation methods.

3.    The complexity of both pilot allocation methods was compared to show the respective scalability performance. 

2.       System Model 

          Uplink communication is considered from K UEs to L APs equipped with N antennas, while only a single-antenna is used at UEs. The more practical time-division duplexing (TDD) mode selected, such that during  channel coherence time, channels were allocated for uplink data transmission and pilot training respectively. UEs and APs were uniformly distributed in a wrapped-around square area.

2.1. Channel Model

       A quasi-static fading model was adopted (Aziz et al., 2022) because the channel remained constant during each coherence block of duration  and varied independently from one block to another. In each block, channels were used for training and data transmission, respectively. The channel from UEs k to APs  was denoted as  and assumed to be a correlated Rayleigh fading channel  The matrix  described the spatial correlation among the channel elements in terms of large-scale fading. The large-scale fading power between UE k to AP  was analyzed by Bjornson and Sanguinetti (2020), and expressed in (equation 1).

where tr(.) is the trace of a matrix. The connectivity between the n^th antenna of serving AP  to UE k was defined by a diagonal matrix  The  diagonal entry of  is 1 when there is connectivity, and 0 if otherwise, allowing AP to transmit and decode the UE signal when connected. The matrix represents the user-centric clusters, which are generally overlapping. When  is connected to at least one  AP  antenna, also translated as  The subset of UEs connected to AP  was denoted as  Concatenating the connectivity matrix      for all L APs diagonally formed a block-diagonal matrix  Clusters of two different overlap, which means these were connected to the same APs, either partially or completely. 

2.2. Pilot Training

Pilot training aimed to estimate the UEs channels at APs. In order to obtain a scalable system, APs were only required to estimate a subset of UEs channels, which were then used to combine the received signal (Bjornson and Sanguinetti, 2020). This process is known as the local partial minimum mean square (LP-MMSE) combiner.

The  mutually orthogonal pilots were used for training purposes, where the number of UEs served by APs were assumed at most  pilot signals, where each was denoted as The limited number of pilots  was due to spectrum availability. However, the number of UEs K was more significant than , and the pilots were reused among different UEs. The set  consisted of UEs, where each was allocated to pilot index  During training, AP   received the uplink pilot signal  from the UEs in set , as provided in (equation 2).

The parameters define the processing gain and transmit power, respectively. Moreover,  is the additive white Gaussian noise (AWGN), distributed as 

Due to the limited availability of channels, the UEs in set  share the same pilots. This resulted in the received signal for UE k containing channels from other UEs k. Therefore, the channel estimation of UEs in set  becomes correlated, leading to a phenomenon known as pilot contamination. The contaminated pilot degraded the performance of the channel estimator and consequently reduced the spectral efficiency. The MMSE channel estimate of  was expressed in (equation 3).

where is the correlation matrix of the received signal expressed in (equation 4).

2.3. Data Transmission

       During uplink data transmission, each AP received signals from all K UEs, as given in (equation 5).

The parameter  represents the symbol of UEs j transmitted with power P_j. The uplink data can be decoded in two ways (Bjornson and Sanguinetti, 2020). 

1) Centralized processing: APs send the received uplink signals during training and data transmission, i.e.,  respectively, to the CPU. This scheme requires significant bandwidth on the fronthaul link.

2) Distributed processing: APs independently send the local estimate of the data symbols to the CPU. Channel estimation was also performed locally in this scheme. It required significantly fewer bandwidth for fronthaul link and less CPU load.

This research focused on the distributed processing scheme. After channel estimation, APs applied the LP-MMSE combining vector, as provided in (equation 6).


APs are responsible for estimating the channel of the serving UEs, specifically those in  Moreover, the LP-MMSE combiner considered the source of interference for UE k that originated from the remaining UEs currently served by  denoted by  Therefore, this combiner is scalable and the complexity is unaffected by an infinitely large number of UEs. After receiving and combining the signals, APs locally computed the soft estimate of the data symbol of UEs k as defined in (equation 7).

The soft-estimate was sent to the CPU for further processing, combining it with the estimated data symbol of UE k denoted as Due to the lack of channel estimation knowledge at the CPU, the use-and-then-forget (UatF) bound was used to calculate the achievable uplink spectral efficiency. This bound showed that the channel estimates were used to design the combining vector at APs, although it was discarded when calculating the achievable spectral efficiency at the CPU. The achievable spectral efficiency of UEs k can be determined as given in (equation 8).

The combining  was derived from stacking1,2, .. L. Similarly,  was obtained from stacking  is Kronecker product and  is identity matrix of size L.

3.     Joint User-Centric Clustering and Pilot Assignment

A strategic method to associate UEs with APs and allocated pilots effectively is required since the number of UEs is typically larger than the number of available orthogonal pilots. A joint user-centric clustering and pilot allocation method designed for a scalable cell-free massive MIMO system was proposed to address this challenge.

3.1. Proposed Method

     The Gale-Shapley clustering (Lin et al., 2018) was combined with existing pilot allocation methods, namely the scalable (Bjornson and Sanguinetti, 2020) and graph-coloring methods (Liu et al., 2020b). This algorithm which was previously applied to UDN, considered the maximum traffic-load at APs as constraint. However, the constraint was omitted and instead equivalently limited the number of serving UEs at each AP by the available orthogonal pilots 
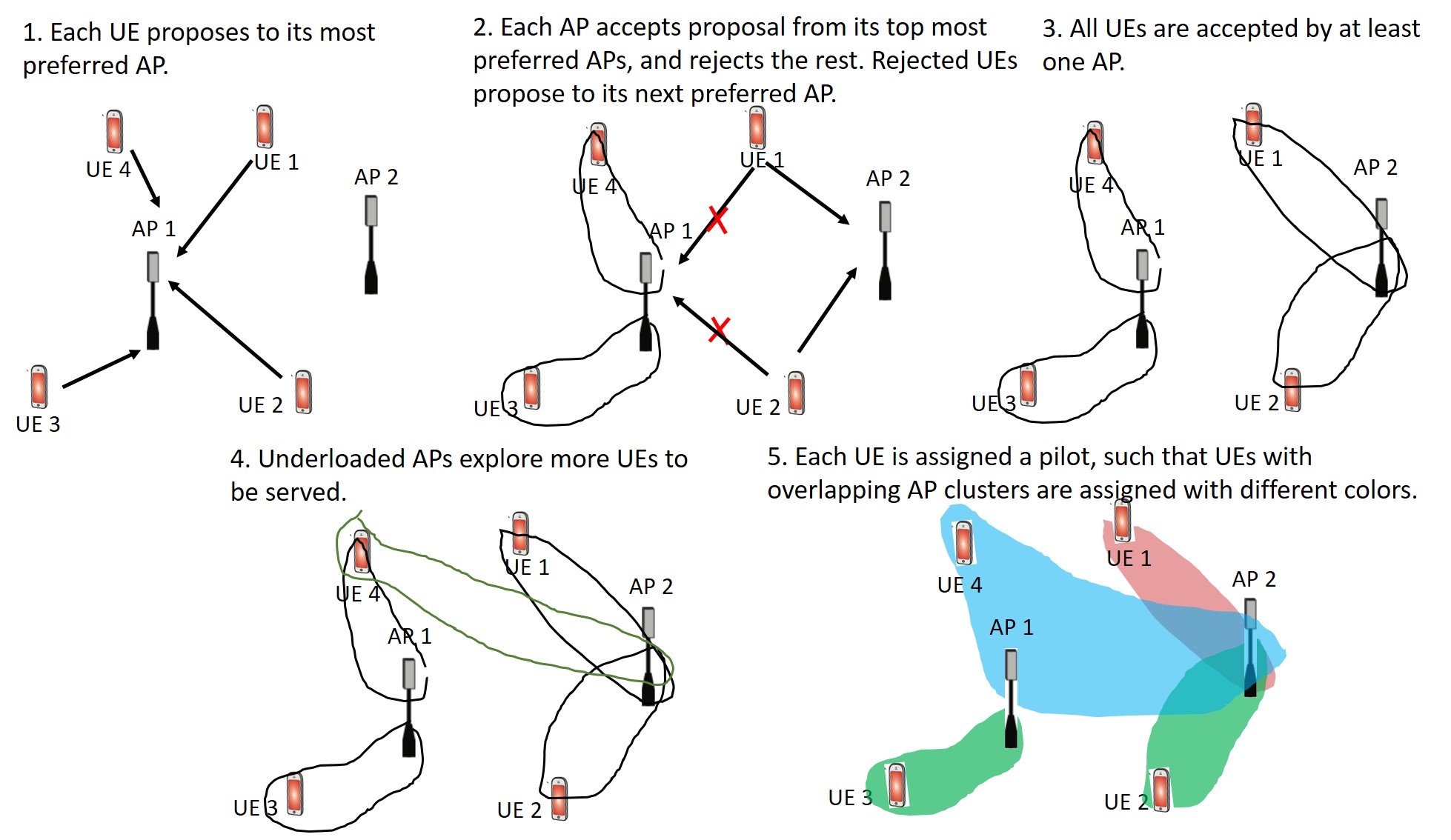
    According to Lin et al. (2018),  clustering comprised of two stages, namely anchoring and exploration. Initially, UEs measured the large-scale fading  from the received synchronization signal and generated the preference list based on these measurements. APs produced the preference list using the same steps. To determine the anchor AP, UE proposed the most preferred AP which had not been rejected initially and is waiting for acceptance or rejection. Meanwhile, each AP retained all UE proposals until the limit  was reached, after which it kept only  best channel UEs and rejected the rest. The rejected UEs then proposed to the following preferred AP, and the process is repeated until the proposal of a given UE is either accepted or all proposals are rejected by all APs in the preference list of the UE.

The exploration stage was conducted only for APs with fewer associated UEs less than  This is different from the method proposed by Lin et al. (2018), where the maximum traffic- load at APs was considered. To ensure UEs with acceptable channel conditions, a threshold  was defined. It is essential to set  to a low enough value such that more UEs will be served by APs. For UEs with firstly sorts them and then associates with the top  list, as long as the total number of UEs, including those from the anchoring stage, does not exceed  At the end of the exploration stage, each UE can be associated with more than 1 APs leading to many-to-many matching. In addition, the subset of APs serving a given UE may partially overlap.

Two pilot allocation methods, namely scalable, non-graph based, and graph methods, were examined.

3.1.1. Scalable Method

The scalable pilot assignment method (Bjornson and Sanguinetti, 2020) was applied to the constructed clusters. Firstly, the joint clustering and pilot assignment, in the original form, were briefly introduced. In the process, UEs selected master AP that had the best channel among its surrounding APs. Subsequently, the master AP assigned the least pilot contamination among the  available option. The surrounding APs determined whether to jointly serve the new UE based on the absence of currently served UEs using the same pilot or if the interference level of the allocated pilot signal is not significantly larger than that measured from its master AP. 

The scalable method does not guarantee that UEs served by a given AP have orthogonal pilots as opposed to the Gale-Shapley exploration stage, which rejected UEs based on the large-scale fading coefficient  This led to two potential outcomes. Firstly, there may be more  UEs designating the same master AP, causing it to allocate pilots with the least corresponding interference level. Secondly, the surrounding APs serve the new UE, which has the same pilot already allocated to its currently served UE.  

The research focused solely on the anchoring stage of the Gale-Shapley algorithm with anchor AP as the master (Bjornson and Sanguinetti, 2020). Moreover, it only accepted proposals from at most  best channel UEs. The process guaranteed orthogonal pilots were assigned to the associated UEs, as opposed to the original version (Bjornson and Sanguinetti, 2020). Similar to the original version, after finding an anchor AP, the surrounding APs jointly served the new UE when they have no UEs served using the same pilot as the new UE or when the interference level of the allocated pilot signal was not significantly larger than that measured from its master AP.
3.1.2. Graph-coloring Method

After defining the user-centric clusters, the next step entailed pilot allocation to each cluster. In the context of graph-coloring, each UE is defined as a vertex. Furthermore, two UEs with overlapping clusters were connected by an edge, indicating that at least common APs served the purpose. The connected vertices known as adjacent vertices were assigned orthogonal pilots to prevent the adverse impact of pilot contamination on the system performance. However, due to the limited number of available pilots, designing an effective allocation scheme challenges. The graph-coloring method (Liu et al., 2020b) was used to allocate the limited number of orthogonal pilots to the user-centric clusters.

Graph-coloring aims to minimize the number of colors applied to the vertices, ensuring that that adjacent ones have different colors (Chartrand and Zhang, 2019; Formanowicz and Tanas, 2012; Cheng et al., 2005). Initially, the algorithm calculates the degree of each vertex, which is defined as the number of connected edges.  The vertex with the highest degree is colored first. Subsequently, the saturation degree of adjacent vertices was updated, indicating the number of unique colors assigned. The next vertex to be colored was selected based on the one with the maximum saturation degree. These steps were repeated until all vertices were colored. However, when the total number of colors is not equal to  the clustering exploration stage must be repeated. During this stage, the threshold  is either increased or decreased, depending on whether the number of colors is higher or lower than the available  colors, respectively.

Figure 1 CDF of spectral efficiency per UE for increasing number of UEs; number of pilots available 

 3.2. Complexity Comparison

     The complexity comparison was performed between the two pilot allocation methods. Based on calculation provided in (Chen et al., 2021), the scalable pilot allocation method has a complexity order of  while the graph-coloring pilot assignment is of order This suggested that the scalable pilot allocation method offered better scalability as 

The system performance was evaluated in terms of the CDF of spectral efficiency per UE for an increasing number of UEs and available pilots. However, since the main aim of cell-free massive MIMO is to provide uniform service for all UEs in the network, this research focused on the 95%-likely spectral efficiency to measure the performance of the lowest 5% UE accurately. The number of UEs considered were  while the available orthogonal pilots were  where each was equipped with  antennas. Furthermore, the single-antenna UE has a transmission power  A large-scale fading channel model similar to the one designed by Bjornson, Hoydis, and Sanguinetti (2017) was adopted. The channel coherence time was set at 200 blocks, allocating  blocks for data transmission. During the exploration stage, a default threshold  was used. Both UEs and APs were uniformly distributed in a 500-meter-square wrapped-around area.
        Figure 1 shows the CDF of spectral efficiency per UE when each AP serves at most  As the number of UEs increases, both the graph and scalable pilot allocation schemes experience decline in because more UEs translate to higher inter-cluster interference in the network. This is a consequence of the low complexity combining vector, which mainly suppresses the interference signals from UEs served by the given APs, as stated in Eq. (6). The performance of the graph pilot allocation method is worse than the scalable at lower spectral efficiency values, and vice versa. The limitation of  pilots per AP in the scalable method leads to severe pilot contamination when the master AP serves more than 5 UEs, resulting in reduced spectral efficiency, particularly evident in the upper part of Figure 1. However, the graph-coloring only allocated orthogonal pilots when common APs serve two different UEs. To fulfill the restricted number of pilots, the graph method reduces the number of cooperating APs for a given UE. This leads to less spatial diversity, which impacts the UEs with low to moderate channel conditions, resulting in lower spectral efficiencies compared to the scalable method.

Figure 2 CDF of spectral efficiency per UE for increasing number of UEs; number of pilots available 

The CDF of spectral efficiency per UE was compared as the number of orthogonal pilots increased from  shown in Figure 2. Similar to the scenario of having  pilots per AP, as the number of UEs is increased, the UE rate decreases. Additionally, both the graph and scalable methods had similar performance when there were more pilots in the system. This is because a greater number of orthogonal pilots reduced the impact of pilot contamination for the scalable method, leading to a uniform increase in UEs spectral efficiency for all UEs. However, increasing the number of pilots for the graph method significantly benefited UEs with low spectral efficiency. This was proven by the lower part of the spectral efficiency curve in Figure 1, which rose as the number of pilots increased in Figure 2. The reverse was the case in the upper part of the curve because each AP served more UEs when the number of pilots was increased. However, the UEs that initially had high spectral efficiency were sacrificed due to increased inter-cluster interference. As a result, increasing the number of pilots provided uniformly superior performance for both pilot allocation methods.

The 95%-likely spectral efficiency for all scenarios showed that the scalable method is superior compared to the graph method. For example, in Figure 1, when  the scalable and graph methods obtained a 95%-likely spectral efficiency of 1.370 and 0.673, respectively. Increasing the number of UEs to  while ensuring the number of pilots fixed, the 95%-likely spectral efficiency reduces to 0.063 and 0.050 for the scalable and graph methods, respectively.

When the number of UEs in the network is low, such as 50, the APs are associated with distant UEs. Due to the insufficient number of pilots, the subset of serving APs was reduced since the graph method needed to assign different colors to adjacent vertices. Therefore, the spectral efficiency per UE of the graph method is much lower. The scalable method tends to allocate the same pilot to overlapping clusters. When the number of UEs is fewer, the average distance is high, causing the impact of inter-cluster interference to be compensated with the benefit of associating each UE with more serving APs.

Increasing the number of available pilots to  increases the 95%-likely spectral efficiency across all UEs scenario for both methods, as shown in Figure 2. For example, when  the scalable and graph methods produced 95%-likely spectral efficiencies of 1.922 and 1.682, respectively. In contrast, the corresponding spectral efficiencies were 0.202 and 0.093 when  . The increased availability of pilots reduced the impact of pilot contamination, leading to enhanced spectral efficiency. The graph method produced more APs serving a given, significantly improving the performance. Despite this fact, the scalable method remains more attractive, since it provides a uniformly superior performance with lower complexity.

        In conclusion, a joint user-centric clustering and pilot allocation method was for scalable cell-free massive MIMO systems aimed at providing uniform spectral efficiency for all UEs in the network. The performance of the graph pilot allocation method was particularly sensitive to the insufficiency of orthogonal pilots, as it relied on following the chromatic number of the graph. UEs were served by a lesser number of APs, which deteriorated the respective spectral efficiencies. Despite the uniformly superior performance, the scalable pilot allocation method had lower complexity, making it a feasible choice for realizing a scalable cell-free massive MIMO system, especially in scenarios with higher UE density. The analysis provided uniform power transmitted from all UEs with interest in optimization despite the higher complexity and signalling overhead required. UEs were assumed static throughout the research, therefore, evaluating the impact of UEs mobility on the system performance was suggested for future investigations.

The authors are grateful for the funding support provided through the 2022 P2MI ITB research grant.

Alonzo, M., Buzzi, S., 2017. Cell-Free and User-Centric Massive MIMO at Millimeter Wave Frequencies. In: Proceedings 2017 IEEE 28^th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), pp. 1–5, DOI: https://doi.org/10.1109/PIMRC.2017.8292302

Alruwaili, M., Kim, J., Oluoch, J., 2024. Optimizing 5G Power Allocation with Device-to-Device Communication: A Gale-Shapley Algorithm Approach. IEEE Access, Volume 12, pp. 30781–30795, DOI: 10.1109/ACCESS.2024.3369597

Ammar, H.A., Adve, R., Shahbazpanahi, S., Boudreau, G., Srinivas, K.V., 2022. User-Centric Cell-Free Massive MIMO Networks: A Survey of Opportunities, Challenges and Solutions. IEEE Communications Surveys & Tutorials, Volume 24(1), pp. 611–652, DOI: 10.1109/COMST.2021.3135119

Aziz, A.A., Mohamad, H.A., Mahmud, A., Alias, M.Y., Hasan, N., 2022. Space-Time Frequency Block Codes in LTE-DSRC Hybrid Vehicular Networks. International Journal of Technology, Volume 13(6), pp. 1183–1192, DOI: https://doi.org/10.14716/ijtech.v13i6.5828

Bjornson, E., Hoydis, J., Sanguinetti, L., 2017. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency, Foundations and Trends® in Signal Processing, Volume 11(3-4), pp. 154–655, DOI: 10.1561/2000000093

Bjornson, E., Sanguinetti, L., 2020. Scalable Cell-Free Massive MIMO Systems. IEEE Transactions on Communications, Volume 68(7), pp. 4247–4261, DOI: 10.1109/TCOMM.2020.2987311

Buzzi, S., D’Andrea, C., 2017. Cell-Free Massive MIMO: User-Centric Approach. IEEE Communications Letters, Volume 6(6), pp. 706–709, DOI: 10.1109/LWC.2017.2734893

Buzzi, S., D’Andrea, C., Zappone, A., D’Eli, C., 2021. User-centric 5G Cellular Networks: Resource Allocation and Comparison with The Cell-Free Massive MIMO Approach. IEEE Transactions on Wireless Communications, Volume 19(2), pp. 1250–1264, DOI: 10.1109/TWC.2019.2952117

Chartrand, G., Zhang, P., 2019. Chromatic Graph Theory, 1^st ed. Chapman and Hall/CRC. https://doi.org/10.1201/9780429438868

Chen, S., Zhang, J., Zhang, J., Bjornson, E., Ai, B., 2022. A Survey on User Centric Cell-Free Massive MIMO Systems. Digital Communications and Networks, Volume 8(5), pp. 695–719, https://doi.org/10.1016/j.dcan.2021.12.005

Cheng, M.X., Huang, S.C., Huang, X., Wu, W., 2005. New Graph Model for Channel Assignment in Ad Hoc Wireless Networks. In: IEE Proceedings – Communications, Volume 152(6), pp. 1039 –1046, https://doi.org/10.1049/ip-com:20059053

Femenias, G., Riera-Palou, F., Björnson, E., 2023. Another Twist to The Scalability in Cell-Free Massive MIMO networks. IEEE Transactions on Communications, Volume 71(11), pp. 6793–6804, DOI: 10.1109/TCOMM.2023.3305531

Formanowicz, P., Tanas, K., 2012. A Survey of Graph Coloring- Its Types, Methods and Applications. Foundations of Computing and Decision Sciences, Volume 37, pp. 223–238, DOI: 10.2478/v10209-011-0012-y

Gesbert, D., Hanly, S., Huang, H., Shamai (Shitz), S., Simeone, O., Yu, W., 2010. Multi-Cell MIMO Cooperative Networks: A New Look at Interference. IEEE Journal on Selected Areas in Communications, Volume 28(9), pp. 1380–1408, DOI: 10.1109/JSAC.2010.101202

Hmida, W., Meghdadi, V., Bouallegue, A., Cances, J.P., 2020. Graph Coloring Based Pilot Reuse Among Interfering Users in Cell-Free Massive MIMO. In: Proceedings IEEE International Conference on Communications (ICC), pp. 1–6, DOI: 10.1109/ICCWorkshops49005.2020.9145111

Huang, X., Wang, Y., Chen, S., Li, Y., Wu, Y., 2023. Joint User Clustering and Graph Coloring Based Pilot Assignment for Cell-Free Massive MIMO Systems. Sensors, Volume 23(11), p. 5014, https://doi.org/10.3390/s23115014

Humadi, K., Trigui, I., Zhu, W., Ajib, W., 2022. User-Centric Cluster Design and Analysis for Hybrid sub-6GHz-mmWave-THz Dense Networks. IEEE Transactions on Vehicular Technology, Volume 71(7), pp. 7585–7598, DOI: 10.1109/TVT.2022.3170518

Interdonato, G., Frenger, P., Larsson, E.G., 2019. Scalability Aspects of Cell-Free Massive MIMO. In: Proceedings 2019 IEEE International Conference on Communications (ICC), pp. 1–6, DOI: 10.1109/ICC.2019.8761828

Larsson, E.G., Edfors, O. Tufvesson, F., Marzetta, T.L., 2014. Massive MIMO for Next Generation Wireless Systems. IEEE Communications Magazine, Volume 52(2), pp. 186–195, DOI: 10.1109/MCOM.2014.6736761

Lin, Y., Zhang, R., Li, C., Yang, L., Hanzo, L., 2018. Graph-Based Joint User-Centric Overlapped Clustering and Resource Allocation in Ultradense Networks. IEEE Transactions on Vehicular Technology, Volume 67(5), pp. 4440–4453, DOI: 10.1109/TVT.2017.2787802

Liu, A., Lau, V.K.N., 2017. Joint BS-user Association, Power Allocation, and User-Side Interference Cancellation in Cell-Free Heterogeneous Networks. IEEE Transactions on Signal Processing, Volume 65(2), pp. 335–345, DOI: 10.1109/TSP.2016.2620962

Liu, H., Zhang, J., Jin, S., Ai, B., 2020b. Graph Coloring Based Pilot Assignment for Cell-Free Massive MIMO Systems. IEEE Transactions on Vehicular Technology, Volume 69(8), pp. 9180–9184, DOI: 10.1109/TVT.2020.3000496

Liu, H., Zhang, J., Zhang, X., Kurniawan, A., Juhana, T., Ai, B., 2020a. Tabu-Search-Based Pilot Assignment For Cell-Free Massive MIMO Systems. IEEE Transactions on Vehicular Technology, Volume 69(2), pp. 2286–2290, DOI: 10.1109/TVT.2019.2956217

Lu, L., Li, G.Y., Swindlehurst, A.L., Zhang, R., 2014. An Overview of Massive MIMO: Benefits and Challenges. IEEE Journal of Selected Topics in Signal Processing, Volume 8(5), pp. 742–758, DOI: 10.1109/JSTSP.2014.2317671

Marzetta, T.L., 2015. Massive MIMO: An Introduction. Bell Labs Technical Journal, Volume 20, pp. 11–22, DOI: 10.15325/BLTJ.2015.2407793

Ngo, H.Q., Ashikhmin, A., Yang, H., Larsson, E.G., Marzetta, T.L., 2017. Cell-Free Massive MIMO Versus Small Cells. IEEE Transactions on Wireless Communications, Volume 16(3), pp. 1834–1850, DOI: 10.1109/TWC.2017.2655515

Papazafeiropoulos, A., Björnson, E., Kourtessis, P., Chatzinotas, S., Senior, J.M., 2021. Scalable Cell-Free Massive MIMO Systems: Impact of Hardware Impairments. IEEE Transactions on Vehicular Technology, Volume 70(10), pp. 9701–9715, DOI: 10.1109/TVT.2021.3109341

Sabbagh, R., Pan, C., Wang, J., 2018. Pilot Allocation and Sum-Rate Analysis In Cell-Free Massive MIMO Systems. In: Proceedings 2018 IEEE International Conference on Communications (ICC), pp. 1–6, DOI: 10.1109/ICC.2018.8422575

Teng, Y., Liu, M., Yu, F.R., Leung, V.C.M., Song, M., Zhang, Y., 2019. Resource Allocation for Ultra-Dense Networks: A Survey, Some Research Issues and Challenges. IEEE Communications Surveys & Tutorials, Volume 21(3), pp. 2134–2168, DOI: 10.1109/COMST.2018.2867268

Teo, C.-P., Sethuraman, J., Tan, W.-P., 2001. Gale-Shapley Stable Marriage Problem Revisited: Strategic Issues and Applications. Management Science, Volume 47(9), pp. 1252–1267, https://doi.org/10.1287/mnsc.47.9.1252.9784

Venkatesan, S., Lozano, A., Valenzuela, R., 2007. Network MIMO: Over- Coming Intercell Interference in Indoor Wireless Systems. In: Proceeding Conference Record 41st Asilomar Conference on Signals, Systems, and Computers, pp. 83–87, DOI: 10.1109/ACSSC.2007.4487170

Wang, R., Shen, M., He, Y., Liu, X., 2021. Performance of Cell-Free Massive MIMO with Joint User Clustering and Access Point Selection. IEEE Access, Volume 9, pp. 40860–40870, DOI: 10.1109/ACCESS.2021.3056051

Xie, M., Yu, X., Rui, Y., Wang, K., Dang, X., Zhang, J., 2023. Performance Analysis for User-Centric Cell-Free Massive MIMO Systems with Hardware Impairments and Multi-Antenna Users. IEEE Transactions on Wireless Communications, Volume 23(2), pp. 1243–1259, DOI: 10.1109/TWC.2023.3287577

Zeng, W., He, Y., Li, B., Wang, S., 2021. Pilot Assignment for Cell Free Massive MIMO Systems Using a Weighted Graphic Framework. IEEE Transactions on Vehicular Technology, Volume 70(6), pp. 6190–6194, DOI: 10.1109/TVT.2021.3076440

Zhang, L., Yang, S., Han, Z., 2023. Pilot Assignment for Cell-Free Massive MIMO: A Spectral Clustering Approach. IEEE Wireless Communications Letters, Volume 13(1), pp. 243–247, DOI: 10.1109/LWC.2023.3327079

Zhong, B., Zhu, X., Lim, E.G., 2022. Clustering-Based Pilot Assignment for User-Centric Cell-Free mmWave Massive MIMO Systems. In: 2022 IEEE 96^th Vehicular Technology Conference (VTC2022-Fall), pp. 1–5, DOI: 10.1109/VTC2022-Fall57202.2022.10012778