Machine Learning Approach for Early Assembly Design Cost Estimation: A Case from Make-to-Order Manufacturing Industry

Title: Machine Learning Approach for Early Assembly Design Cost Estimation: A Case from Make-to-Order Manufacturing Industry

Authors
Authors and Affiliations

Anas Ma’ruf, Ali Akbar Ramadani Nasution, Raden Achmad Chairdino Leuveano

Corresponding email: maruf@itb.ac.id

Published at : 10 Jul 2024
Volume : IJtech Vol 15, No 4 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i4.5675

Cite this article as:
Ma’ruf, A., Nasution, A.A.R., Leuveano, R.A.C., 2024. Machine Learning Approach for Early Assembly Design Cost Estimation: A Case from Make-to-Order Manufacturing Industry. International Journal of Technology. Volume 15(4), pp. 1037-1047

Downloads

Anas Ma’ruf	Faculty of Industrial Technology, Bandung Institute of Technology, Jl. Ganesha 10, Bandung, 40132, Indonesia
Ali Akbar Ramadani Nasution	Faculty of Industrial Technology, Bandung Institute of Technology, Jl. Ganesha 10, Bandung, 40132, Indonesia
Raden Achmad Chairdino Leuveano	Department of Industrial Engineering, Faculty of Industrial Engineering, Universitas Pembangunan Nasional “Veteran” Yogyakarta, Jl. Babarsari 2, Yogyakarta, 55281, Indonesia

Email to Corresponding Author

Abstract

Machine Learning Approach for Early Assembly Design Cost Estimation: A Case from Make-to-Order Manufacturing Industry

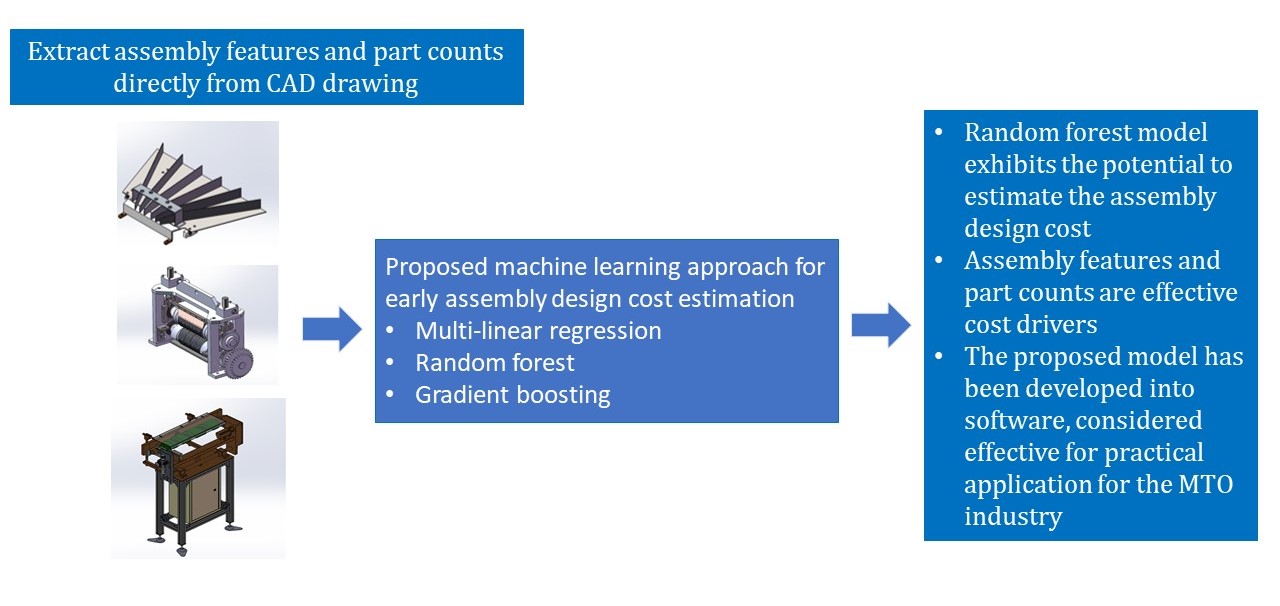
Estimating production costs is a challenging process for the Make-To-Order (MTO) industry because of the product varieties, which leads to inaccurate cost estimation. The product engineering process requires accurate assembly cost estimation to take strategic decisions, specifically during the early design phase. Therefore, an intelligent machine learning-based approach, namely Multi-linear Regression, Random Forest, and Gradient Boosting, is proposed to estimate the assembly design cost. This estimation is done by identifying the assembly features of the 3D CAD model. The validation results showed that mate and assembly features, as well as the number of parts, are effective cost drives, while Random Forest outperformed other models. The proposed methodology is then implemented in a cost estimation program and applied in the MTO industry. The proposed estimation method deviated an average of 17.4% from the actual assembly design cost, considered acceptable during the early design phase. In conclusion, the proposed model and cost estimation program efficiently help the MTO industry predict assembly design costs.

Keywords

3D CAD; Assembly design; Assembly features; Cost estimation; Machine learning

Introduction

Product customization is increasingly implemented in the manufacturing industry to improve competitiveness. Keil (2024) found that industries are motivated to meet new standards due to competitive pressures, complex customer requirements, and stakeholder expectations. This phenomenon has an impact, particularly on the production of the Make-to-Order (MTO) industry (Yazdi, Fini, and Forsythe, 2021). According to Yi et al. (2023), cost estimation is the quantitative prediction of a product’s cost before completing all product development stages. This implies that the MTO industry needs to estimate product costs quickly and accurately. Unlike cost calculation, cost estimation is based on the assumption that the industry lacks access to manufacturing process data and with no conventional standard cost model (Latief, Wibowo, and Isvara, 2013). Koonce et al. (2003) and Bacharoudis et al. (2021) stated that a systematic method is used for estimating material and machining costs by classifying each material and production operation into individual cost drivers.

Estimating assembly design cost is a more complex process, that includes intangible aspects, such as assembly parts and complexity (Castellani, Otri, and Pham, 2019; Demir et al., 2023). In the final design phase, the method used to estimate assembly design cost for mass production is significantly more developed. H’mida, Martin, and Vernadat (2006) and Niazi et al. (2006) have stated that this approach involves outlining the design activities cost, followed by identifying resources and operations during the design phase. Quintana and Ciurana (2011) have suggested that assembly design cost estimation is often performed by using a knowledge-based system, which is typically used in repetitive production.

With these points, this study proposes systematic assembly design cost estimation as an alternative to the conventional MTO approach. Conventional cost estimation is by constructing a regression model based on complex relationships (Verlinden et al., 2008). Also, the choice of method is based on the limited access to manufacturing process data. Hence, the estimation accuracy significantly affects industry profits. This implies that a very low price reduces profits, while an extremely high price tends to affect customer satisfaction negatively (Kalscheuer et al., 2023).

This study examines cost issues related to initial assembly design in the MTO industry. It has been observed that the industry produces a small volume of various assembly products, including precision molding, stamping dies, precision spare parts, and mechanical devices. The assembly design initiates the product’s engineering process based on customer orders using specific 3D Computer-Aided Design (CAD) software. At this phase, accurate cost estimation is essential for making strategic decisions in the engineering process (Post et al., 2020). However, these detailed product features are typically not available when using a conventional cost accounting approach. This caused Alfadhlani et al. (2019) to conclude that CAD data is needed when identifying feature information based on assembly design, saved as historical data of industry orders. To estimate accurate assembly design costs, it is necessary to establish a relationship between the product features and the historical assembly design cost. However, using the conventional approach, it is challenging for cost engineers to determine the product's sufficient cost function and behavior based on experience (Bodendorf, Merkl, and Franke, 2021). Machine Learning (ML) method can be applied to solve classification and prediction problems (Dawangi and Budiyanto, 2021; Alas and Ali, 2019; Fagbola, Thakur, and Olugbara, 2019). ML method, as proposed by Durodola (2022), Hammann (2024), and Ning et al. (2020), is an efficient and accurate technique for identifying the relationship between features and historical product cost. The model is typically employed to overcome this problem as it detects hidden functional relationships between assembly features and costs (Bodendorf, Merkl, and Franke, 2021). Other approaches to assembly cost estimation are analytical, knowledge-base, or hybrid approaches (Mencaroni et al., 2023; Hagemann and Stark, 2020; Burggräf et al., 2019).

The main objectives of this study are (1) to propose the ML method as a model for estimating assembly design costs based on 3D CAD data and (2) to create a program-based Graphical User Interface (GUI) that engineers can use to quickly predict assembly design costs. In the MTO industry, it is observed that customers always want to know the product price ahead of time, and as a result, the preliminary price is expected to be close to the final price.

Experimental Methods

Figure 1 shows the detailed procedure for estimating the cost of designing product assemblies. The three major steps for solving cost estimation problems are discussed in the following subsection.

Figure 1 Implementation procedures of assembly design cost estimation

2.1. Data Collection of Assembly Features, Costs, and Pre-Data Processing

The case study in this research focuses on the MTO industry, which produces small volumes and various parts assembled into a product. Furthermore, historical demand orders received from the industry for 3D CAD files were gathered and stored as assembly design information. Figure 2 shows that the process of identifying the assembly cost driver from CAD drawing, which includes 20 mate and 14 assembly features, as well as parts numbers. These assembly features are common CAD operations used to construct an assembly design. For example, the concentric assembly feature is used to define two assembly parts sharing the same axis.

Figure 2 The assembly features used to early estimate the assembly design costs

Furthermore, to estimate target costs, actual product cost data collected based on each 3D CAD file were used. The MTO company specifically evaluated these models to ensure the cost values were consistent with their estimates. Data preprocessing was employed after data collection since it is impossible to directly use the 3D CAD information as input for the ML method. This step is crucial when analyzing the mate and assembly features, as well as the number of parts that affect assembly design costs. Therefore, the transformation of raw data into datasets began with developing a program to extract the features in the 3D CAD file. After this extraction, data cleansing, feature selection, and data transformation were performed.

Subsequently, an Application Programming Interface (API) was utilized to read the 3D CAD file (Malpass, 2011). A command program was then created using Python programming language, which generated a loop in data reading, sequentially stored into data frames, known as the ML model’s input dataset.

Data cleaning is performed to remove several inconsistent features in the data, considering imbalanced data and outliers to improve the quality of cost estimation (Dogan and Birant, 2021). This rationale is because not all 35 assembly features present a value related to the case study. After analyzing data containing empty values and outliers, the assembly features were reduced to 23 variables, which were tested using the ML methods and re-analyzed to determine their performance. The feature selection technique applied Recursive Feature Elimination (RFE) method to select the critical variables that support the model and its performance. As shown in Figure 2, 18 features were identified as critical cost drivers.

The final step in the pre-processing was data transformation, in which variable characteristics based on 3D CAD had to suit the ML method. It was observed that only the multi-linear regression method exhibited distinct characteristics. Hence the variable data needed to be transformed using min-max normalization-based feature scaling. This selection was because multi-linear regression is a distance-based algorithm. Consequently, the dataset for ML methods was categorized into two sets, namely data training, and testing, in which the former was used to train the model, while the latter evaluated its performance. Wang et al. (2020) stated that the dataset was typically divided into 80% training and 20% testing.

2.2. Develop Early Assembly Design Cost Estimation Model-based ML methods

The ML method was chosen to map the complex relationship between assembly design features and costs, based on the input data, namely assembly features used to estimate the initial assembly design costs. Therefore, this study proposes three ML methods, including Multi-linear Regression, Random Forest, and Gradient Boosting, which each was developed and programmed with Python code.

2.2.1. Multi-linear regression model

In this study, several input variables were defined, and the Multi-linear Regression (MLR) model was applied to model the relationship between these inputs and a target variable, which is the assembly design costs. The technique was conducted by fitting a linear equation to the observed data as expressed in Equation (1).

where

is the predicted value,

denotes the

with all parameters set to zero,

represents the

independent variable for

observation,

Meanwhile,

denote the regression coefficients that indicate changes in

relative to a one-unit change in

respectively. For the

independent variable,

is the model’s random error or residual term.

2.2.2. Random forest model

Random Forest (RF) is a supervised ML algorithm that uses a tree-based ensemble learning to predict the output by combining various Decision Trees (DT) (Montesinos López et al., 2022; Rakhra et al., 2021). It is important to note that DTs exhibited distinct observations from the construction of a single DT. The RF algorithm representation using bootstrapping is shown in Figure 3. Bootstrapping uses distinct subsets of the available features to train multiple decision trees concurrently on different subsets of the training data set.

Figure 3 Implementation of RF prediction on a dataset that has 18 features

and 1 output

for th observation,

Furthermore, a random feature selection was chosen based on the aggregation to train several decision trees in parallel (Misra and Li, 2020). Each tree was trained with a unique set of training data and features. This is carried out to ensure that every decision tree is different from the others, which can lower the variance of the RF model as a whole. The RF model integrates the judgments made by each tree in order to achieve superior generalization outcomes.

To obtain a good estimation result, the RF model has hyperparameters that need to be tuned, as shown in Table 1. These include 1) estimator, which is the number of trees in the forest, 2) Max features representing the maximum number of RF features allowed in a single tree. Three max feature parameter settings are applied respectively: a number of features (auto), square root (sqrt), and logarithm (log), 3) Max depth, which denotes the tree’s maximum depth, 4) Min sample split is the minimum number of data points required in a node before splitting, and 5) Min sample leaf, which refers to the minimum number of data points allowed in a leaf node. In ML, Grid Search Cross Validation (GSCV) was further employed to tune these parameters by selecting those with optimal combinations. Table 1 summarizes the search space values for these parameters.

Table 1 Hyperparameters search space in GSCV

Parameter	Range
estimator	{10,50,100}
Max features	{‘auto’, ‘sqrt’, ‘log’}
Max depth	{5, 10, 18, None}
Min sample split	{2, 5, 10, 18, None}
Min sample leaf	{1, 5, 10, 18, None}

2.2.3. Gradient boosting model

The Gradient Boosting (GB) model is a set of DT that uses an ensemble method similar to the RF (Ozcan et al., 2024). The difference between the GB and the RF models was that the latter constructs each tree independently, while the former builds one tree at a time. Furthermore, RF combine results at the end of the process via the majority or average rule, but the GB model combines results immediately after they are produced by correcting errors in the pre-trained tree. Figure 4 illustrates how the GB algorithm employs the sequential ensemble method based on the case being studied.

Figure 4 The representation of the GB algorithm for the case being studied.

To expand the model's capability, the GB algorithm creates a number of regression trees over time. In a forward stepwise manner, the iteration of training process of the GB model to determine the proximate predicted value and the output is expressed in Equation (2) (Wang et al., 2020).

where

is the predicted value,

represents the real target output prediction, and

denotes the decision tree’s number for boosting. Meanwhile,

is the learning rate that meets

for shrinking the contribution of individual decision trees. The structure of the

which is all units of a tree, including leaf and branch nodes, is denoted by

while

represents a function of

without shrinkage, utilizing a predictor variable

to approximate

with tree structure

Table 2 Hyperparameter of the GB model

Parameter	Range
estimator	{10,50,100}
Learning rate	{0.1, 0.3, 0.5, 1}
Max depth	{3, 5, 10, 20, None}

2.2.4. Validating the estimation accuracy of ML models
The ML method produces prediction output for the observation where = 1, 2,…, . Each evaluation of the prediction output requires a model performance measure. The performance metric was used to validate the accuracy of the model when estimating actual assembly design cost, as described by Li et al. (2021). To accurately reflect the magnitude of the actual prediction error, the Mean Absolute Percentage Error (MAPE) and R² techniques were employed, as expressed mathematically in Equations (3) and (4).

where is the predicted value, represents the real target output, and denotes the observed numbers. After evaluating the ML model’s accuracy, the final step entails the selection of the best model to estimate assembly design cost. It was observed that the model with the lowest MAPE and which was closest to one, exhibited the most accurate estimate for early product assembly design costs.

2.3. Develop a Program of Estimated Costs of Product Assembly Design

The assembly features, and the best model selected in the previous step served as a reference when developing the application program of the proposed methodology. Furthermore, the program aims to assist the industry in efficiently predicting the assembly design cost based on the 3D CAD file.

Results and Discussion

A total of 104 historical datasets were collected on the CAD assembly file, which includes the real assembly design of a MTO company. Upon the completion of the dataset, the cost estimation model was developed, trained, fine-tuned, and tested using the proposed methodology, as shown in Figure 1. The three proposed models, namely MLR, RF, and GB, were employed to estimate the product assembly design cost using training datasets. Table 3 shows the final experimental results of the proposed model when tested with 20% datasets, while the results of training with 80% of the datasets are omitted due to its brevity.

As observed in Table 3, the MLR algorithm has no hyperparameters, and hence no tuning was performed, and the and MAPE results obtained were 0.21 and 53%, respectively. Furthermore, only the five best combinations measured by and MAPE is shown in Table 3. The results showed that the RF-91 and the GB-43 models, with respective scores of 26.70% and 32.27% had the least significant MAPE values, while the RF-421 and GB-43 achieved the most significant score. Consequently, the GB-43 and RF-91 were selected as the best among their corresponding models, despite the RF scoring the highest and lowest MAPE. The optimum model was then determined by comparing the performance of MLR, RF-91, and GB-43 when predicting the best hyperparameter architecture.

Table 3 Best result of the MLR, RF, and GB models

Also, a re-experiment was conducted to fit each model using all the training data. Every model’s cost was estimated with the testing data to ensure that the best has the least significant MAPE value and the most negligible difference in between training and testing data. It was observed that the model was stable and exhibited excellent generalization abilities. The respective models predicted performance value based on training and testing data are presented in Table 4. The result showed that the RF outperformed the other models, and therefore it was selected as the best. Moreover, Figure 5 shows the developed application program for estimating the assembly design cost.

Table 4 Comparison of the model’s performance

Figure 5(a) depicts the program-based GUI where the user input a CAD assembly file. The program then uses the CAD's API to automatically identify the number of assembly features and the number of parts, as shown in Figure 5(b). Based on the proposed method, the user is subsequently presented with the estimated assembly design cost.

After selecting the RF model, the best hyperparameters setting was employed to train the data in the application program. The program became the reference for the user to evaluate the assembly design cost. It is important to note that the assembly design cost program was estimated using the proposed method. This method showed deviations ranging from 6.8% to 35.5%, with an average deviation of 17.4% from the actual assembly design cost. In a similar study, Molcho et al. (2014) reported an average deviation of 35% for early design cost estimation. Another advantage of the proposed method is its simplicity; it requires input data solely from CAD data, whereas Kurasova et al. (2021) require subjective input from the user, such as the level of product complexity.

Figure 5 A program for assembly design estimation cost, (a) the user interface and (b) identified cost drivers consisting of mate features, assembly features and the number of parts

The results of the cost estimation model and program development were discussed with the company engineers, who discovered that two assembly design cases presented a substantial predictive error value. Further analysis revealed that the product assembly size was larger than in normal cases. In essence, when the product’s size increases, the material volume required tends to be more, thereby causing extra assembly design costs. This simply implies that the prediction model was limited in estimating the design cost of homogeneous-sized product assembly. Based on these findings, the proposed prediction model was accepted for use during the early stage of assembly design.

Conclusion

This study examined the challenges encountered when estimating the assembly design cost of the MTO industry. Cost estimation entails early evaluation of various assembly parts, particularly when information is limited. The proposed ML method for addressing the challenge was found to be systematic, consistent, fast, and free of subjectivity. The MLR, GB, and RF models are the ML method utilized to estimate the assembly design cost. The experimental result showed that the RF model exhibits the significant potential to efficiently estimate the assembly design cost with an average deviation of 17.4% from the actual assembly design cost. Therefore, the proposed model was developed into a practical application program for MTO industries and considered viable for early assembly design cost estimation where manufacturing information is incomplete. The model has been integrated with CAD software to expedite and maintain consistency in assembly design cost estimation. Nonetheless, the limitation of the proposed model relies on the consistency of the historical dataset used for training the model. Future research is directed to explore the impact of dynamic motions such as assembly motion and kinematic behavior in assembly design cost estimation.

References

Alas, M., Ali, S.I.A., 2019. Prediction Of The High Temperature Performance Of A Geopolymer Modified Asphalt Binder Using Artificial Neural Networks. International Journal of Technology, Volume 10(2), pp. 417–427

Alfadhlani, Samadhi, T. M. A. A., Ma’ruf, A., Toha, I.S., 2019. Automatic Precedence Constraint Generation For Assembly Sequence Planning Using A Three-Dimensional Solid Model. International Journal of Technology, Volume 10(2), pp. 340–350

Bacharoudis, K., Wilson, H., Goodfellow-Jones, S., Popov, A., Ratchev, S., 2021. An Efficient Cost Estimation Framework For Aerospace Applications Using Matlab/Simulink. Procedia CIRP, Volume 104, pp. 1143–1148

Bodendorf, F., Merkl, P., Franke, J., 2021. Intelligent Cost Estimation By Machine Learning In Supply Management: A Structured Literature Review. Computers & Industrial Engineering, Volume 160, p. 107601

Burggräf, P., Wagner, J., Dannapfel, M., Fluchs, S., Müller, K., Koke, B., 2019. Automation Decisions In Flow-Line Assembly Systems Based On A Cost-Benefit Analysis. Procedia CIRP, Volume 81, pp. 529–534

Castellani, M., Otri, S., Pham, D. T., 2019. Printed Circuit Board Assembly Time Minimisation Using A Novel Bees Algorithm. Computers & Industrial Engineering, Volume 133, pp. 186–194

Dawangi, I. D., Budiyanto, M. A., 2021. Ship Energy Efficiency Management Plan Development Using Machine Learning: Case Study Of CO2 Emissions Of Ship Activities At Container Port. International Journal of Technology, Volume 12(5), pp. 925–934

Demir, O. E., Colledani, M., Paoletti, R., Pippione, G., 2023. Function-Based Selective And Adaptive Cyber-Physical Assembly System For Increased Quality In Optoelectronics Industry. Computers in Industry, Volume 148, pp. 103915

Dogan, A., Birant, D., 2021. Machine Learning And Data Mining In Manufacturing. Expert Systems with Applications, Volume 166(15), pp. 114060

Durodola, J. F., 2022. Machine Learning For Design, Phase Transformation And Mechanical Properties Of Alloys. Progress in Materials Science, Volume 123(August 2020), pp. 100797

Fagbola, T. M., Thakur, C. S., Olugbara, O., 2019. News Article Classification Using Kolmogorov Complexity Distance And Artificial Neural Network. International Journal of Technologies, Volume 10(4), pp. 710–720

H’mida, F., Martin, P., Vernadat, F., 2006. Cost Estimation In Mechanical Production: The Cost Entity Approach Applied To Integrated Product Engineering. International Journal of Production Economics, Volume 103(1), pp. 17–35

Hagemann, S., Stark, R., 2020. An Optimal Algorithm For The Robotic Assembly System Design Problem: An Industrial Case Study. CIRP Journal of Manufacturing Science and Technology, Volume 31, pp. 500–513

Hammann, D., 2024. Big Data And Machine Learning In Cost Estimation: An Automotive Case Study. International Journal of Production Economics, Volume 269, pp. 109137

Kalscheuer, F., Koch, J., Schüppstuhl, T., 2023. Reducing Commissioning Efforts For Hybrid Assembly Systems Using A Data-Driven Approach. Procedia CIRP, Volume 118, pp. 935–939

Keil, S., 2024. Competing For Manufacturing Value Added: How Strong Is Competitive Cost Pressure On Sectoral Level? Structural Change and Economic Dynamics, Volume 69, pp. 197–212

Koonce, D., Judd, R., Sormaz, D., Masel, D. T., 2003. A Hierarchical Cost Estimation Tool. Computers in Industry, Volume 50(3), pp. 293–302

Kurasova, O., Marcinkevicius, V., Medvedev, V., Mikulskiene, B., 2021. Early Cost Rstimation In Customized Furniture Manufacturing Using Machine Learning. International Journal of Machine Learning and Computing, Volume 11(1), pp. 28–33

Latief, Y., Wibowo, A., Isvara, W., 2013. Preliminary Cost Estimation Using Regression Analysis Incorporated With Adaptive Neuro Fuzzy Inference System. International Journal of Technology, Volume 4(1), pp. 63–72

Li, E., Yang, F., Ren, M., Zhang, X., Zhou, J., Khandelwal, M., 2021. Prediction Of Blasting Mean Fragment Size Using Support Vector Regression Combined With Five Optimization Algorithms. Journal of Rock Mechanics and Geotechnical Engineering, Volume 13(6), pp. 1380–1397

Malpass, L., 2011. SolidWorks API Series 1: Programming & Automation. AngelSix

Mencaroni, A., Claeys, D., De Vuyst, S., 2023. A Novel Hybrid Assembly Method To Reduce Operational Costs Of Selective Assembly. International Journal of Production Economics, Volume 264, p. 108966

Misra, S., Li, H., 2020. Noninvasive Fracture Characterization Based On The Classification Of Sonic Wave Travel Times. In Machine Learning for Subsurface Characterization. Elsevier Inc

Molcho, G., Cristal, A., Shpitalni, M., 2014. Part Cost Estimation At Early Design Phase. CIRP Annals - Manufacturing Technology, Volume 63(1), pp. 153–156

Montesinos López, O. A., Montesinos López, A., Crossa, J., 2022. Multivariate Statistical Machine Learning Methods For Genomic Prediction. In Multivariate Statistical Machine Learning Methods for Genomic Prediction

Niazi, A., Dai, J. S., Balabani, S., Seneviratne, L., 2006. Product Cost Estimation: Technique Classification And Methodology Review. Journal of Manufacturing Science and Engineering, Volume 128(2), pp. 563–575

Ning, F., Shi, Y., Cai, M., Xu, W., Zhang, X., 2020. Manufacturing Cost Estimation Based On The Machining Process And Deep-Learning Method. Journal of Manufacturing Systems, Volume 56, pp. 11–22

Ozcan, G., Kocak, B., Gulbandilar, E., Kocak, Y., 2024. Efficient Machine Learning Models For Estimation Of Compressive Strengths Of Zeolite And Diatomite Substituting Concrete In Sodium Chloride Solution. Arabian Journal for Science and Engineering

Post, C., Wentingmann, N., Bramsiepe, C., Schembecker, G., 2020. Using Design Spaces For More Accurate Cost Estimation During Early Engineering Phases. Chemical Engineering Research and Design, Volume 153, pp. 592–602

Quintana, G., Ciurana, J., 2011. Cost Estimation Support Tool For Vertical High Speed Machines Based On Product Characteristics And Productivity Requirements. International Journal of Production Economics, Volume 134(1), pp. 188–195

Rakhra, M., Soniya, P., Tanwar, D., Singh, P., Bordoloi, D., Agarwal, P., Takkar, S., Jairath, K., Verma, N., 2021. Crop Price Prediction Using Random Forest And Decision Tree Regression:-A Review. Materials Today: Proceedings

Verlinden, B., Duflou, J.R., Collin, P., Cattrysse, D., 2008. Cost Estimation For Sheet Metal Parts Using Multiple Regression And Artificial Neural Networks: A Case Study. International Journal of Production Economics, Volume 111(2), pp. 484–492

Wang, M. X., Huang, D., Wang, G., Li, D.-Q., 2020. SS-XGBoost: A Machine Learning Framework For Predicting Newmark Sliding Displacements Of Slopes. Journal of Geotechnical and Geoenvironmental Engineering, Volume 146(9), pp. 1–17

Yazdi, A. J., Fini, A. A. F., Forsythe, P., 2021. Mass-Customisation Of Cross-Laminated Timber Wall Systems At Early Design Stages. Automation in Construction, Volume 132, pp. 103938

Yi, L., Werrel, M., Ehmsen, S., Glatt, M., Aurich, J.C., 2023. A Specific Manufacturing Cost Model For Fast Cost Estimation In Additive Manufacturing. Procedia CIRP, Volume 120, pp. 21–26

Download PDF

Who cite this paper

Table of Contents

Article