Power Transformer Load Noise Model based on Backpropagation Neural Network
Corresponding email: danangwijaya@ugm.ac.id
Published at : 18 Sep 2024
Volume : IJtech
Vol 15, No 5 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i5.5548
Pramono, W.B., Wijaya, F.D., Hadi, S.P., Indarto, A., Wahyudi, M.S., 2024. Power Transformer Load Noise Model based on Backpropagation Neural Network. International Journal of Technology. Volume 15(5), pp. 1550-1560
| Wahyudi Budi Pramono | Department of Electrical Engineering, Faculty of Industrial Technology, Universitas Islam Indonesia, Yogyakarta, 55584, Indonesia |
| Fransisco Danang Wijaya | Department of Electrical and Information Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Sasongko Pramono Hadi | Department of Electrical and Information Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Agus Indarto | Elsewedy Electric Indonesia, Bogor Regency 16820, Indonesia |
| Moh Slamet Wahyudi | Elsewedy Electric Indonesia, Bogor Regency 16820, Indonesia |
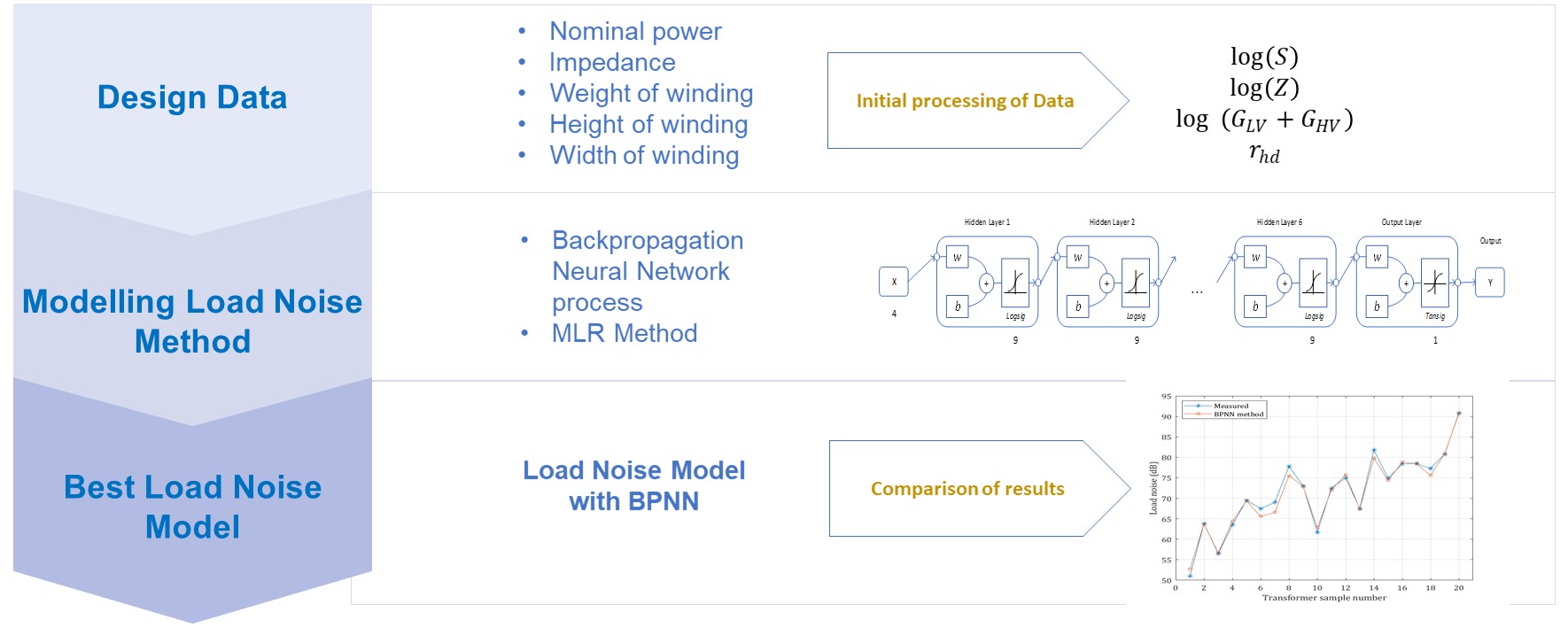
The operation of power transformer in an electric system is the cause of noise in form of sound. At a certain level, this noise can be considered as pollution, interfering with the comfort and health of human hearing. The phenomenon shows the need to understand load noise that is generated during the design process of power transformer. However, a major related problem is the unavailability of an accurate load noise model capable of precise prediction during the design stage. Therefore, this research aimed to develop load noise model based on an artificial neural network for power transformer to predict the generated load noise value. The development process was carried out using a trained backpropagation neural network (BPNN) with the Levenberg-Marquardt algorithm. Before training for neural network, input parameters such as power, impedance, and winding geometry factors were selected and normalized. The linear regression method was used to assess the quality of neural network model training results. For performance comparison, the multiple linear regression (MLR) model and the Reiplinger method were also developed. The results showed that load noise model was developed based on BPNN with seven hidden layers and nine neurons for each layer. Model showed acceptable output variables, with mean absolute percentage error (MAPE), mean absolute error (MAE), root mean square error (RMSE), and correlation coefficient (R) of 0.007, 0.464, 0.708, and 0.998, respectively. Furthermore, the prediction of load noise achieved through BPNN showed significantly high accuracy compared to the existing standard formulas.
Backpropagation; Load noise; Model; Neural network; Power transformer
Power transformer is an essential component in the electric system, playing an important role in meeting the energy demands of customers (Aziz, Indarto, and Hudaya, 2021; Rozhentcova et al., 2020; Indarto et al., 2017). During operation, power transformer generate noise, which can be considered as pollution, potentially disturbing the comfort of surrounding community. This noise is classified into three types, namely no-load, load, and noise caused by the cooling system (Al-Abadi, 2019). Based on classification, no-load noise has an almost constant value during the operation of power transformer (Shilyashki et al., 2016). In contrast, load noise varies significantly depending on the amount of electric current flowing and the winding parameter (Al-Abadi et al., 2017; Rohilla and Palani Samy, 2015). Among these three types, load noise becomes the most dominant source, particularly as power transformer increases (Vasques, Miguel, and Campelo, 2013; Lukic et al., 2012). Load noise is an important aspect that is considered during the design process after power losses, efficiency, dimension, and costs of power transformer. Designers usually use an empirical formula to predict the amount of load noise. However, this formula has not considered all aspects affecting load noise value, resulting in inaccuracies in the predicted values (Paghadar and Kantaria, 2016). Reiplinger has developed the formula for predicting load noise. The formula shows a significant difference in measured value, without considering other variables, such as physical form and electromagnetic force, which are sources of load noise (Girgis, Bernesjö, and Anger, 2009). Therefore, the empirical method must be modified to include other parameters affecting load noise (Lukic et al., 2012). Previous research has included the effect of transformer impedance and the presence of tap winding in the formula to improve the method. Although the results show a better value compared to Reiplinger formula, there is a high standard deviation of 3.5 dB (Girgis, Bernesjö, and Anger, 2009). A new calculation method for load noise caused by windings has also been carried out by considering both radial and axial forces (Yoshida et al., 2021; Witczak and Swiatkowski, 2017), influenced by load current flowing (Kim et al., 2020). The results showed superior measurement accuracy, but the standard deviation is still 1.4 dB (Girgis, Bernesjö, and Anger, 2009). The main problem associated with load noise is the difficulty of accurately quantifying the value of noise generated by transformer. The incompatibility of load noise values against the standards or consumers' specifications poses a significant problem for power transformer manufacturers (Pramono et al., 2021; Pramono, Wijaya, and Hadi, 2020). Several efforts that have been carried out to reduce load noise in power transformer require high costs and a longer time, causing losses to manufacturers. Therefore, knowledge about load noise at the design stage is essential to minimize losses and implement corrective measures (Zhu, Hao, and Lu, 2022).
Based on the background above, this research aimed
to develop load
noise model generated by power transformer based on design data using
backpropagation neural network (BPNN). Generally,
power
transformer parameters have a very complex relationship with each other, leading to difficult application in conventional
mathematical methods. To address this challenge, an
artificial neural network (ANN) offers
a promising solution by effectively modeling
complex system without previous
knowledge of
mathematical relationships (Alas and Ali, 2019; Dhini et al., 2015). In addition, ANN can generalize model to predict outcomes with
new input data,
which are suitable for handling high
data volatility and non-constant variance. One learning method that has been proven effective with good accuracy and speed is backpropagation, providing additional advantages such as minimal parameter tuning
requirements, flexibility, and independence
from
knowledge of network features
(Dhini et al., 2020). This load noise model will incorporate the
main parameters, known as noise sources and others
to provide
accurate values. This research is
organized as follows, the first part discusses the proposed method, consisting of
selecting input parameters and developing load noise model. The second part
presents the result, validation, and comparison. The last part
contains conclusions and opportunities for improvement.
The first step in the proposed is the selection parameters that
significantly affect load noise. Subsequently, the second step is to develop
load noise model using MLR and BPNN methods, while the last step is testing of
model.
2.1. Selection
of The Input Parameters
This research developed model for predicting
load noise by considering the main contributing parameters. During the selection of input parameters, there is a need to consider factors that closely influence
the final model of load noise (Fagbola,
Thakur, and Olugbara, 2019). The parameters used in the development process are the nominal power,
impedance, and winding geometry factor (WGF). Specifically, nominal power is the product of the
current's square and transformer's impedance. The square of current flowing
directly correlates with the electromagnetic force in the winding (Jin
and Pan, 2016; Negi, Singh, and Kr Shah, 2013). Therefore, the nominal power is a parameter
that significantly affects the amount of load noise.
The impedance of power transformer for each phase is
influenced by the number of turns, the axial height of the winding, the winding
width, the duct channel width, the average length of the conductor, and
frequency. Furthermore, the
impedance parameters refer more to the physical geometric shape of the winding (Al-Abadi,
2019). Generally, the current
flowing in the winding produces magnetic flux, causing vibrations that serve as
primary sources of noise (Duan et al., 2018; Al-Abadi et al., 2017; Jingzhu et al., 2016). In the event of a short circuit occurs, the calculation of axial and
radial forces becomes essential. According to (Sathya and Savadamuthu, 2019), axial and radial forces of the winding are
influenced by several parameters of height, diameter, the average diameter of
the two windings, width, and the channel width. As described by (Yu et al., 2022; Lukic et al., 2012), load noise is affected by axial and radial
forces, showing the importance of selecting appropriate impedance
parameters. WGF mechanically influences load noise generated. This is
attributed to WGF, serving as the ratio between the winding height, diameter weight of
and
(Pramono et al., 2023).
2.2.
Selection of The Output Target
BPNN or MLR output in target data containing
load noise data was measured in this research. The measurement of load noise was carried out on power transformer
during short circuit testing. Although the current flowing was nominal, the input voltage was not more than 10% of nominal
voltage. Therefore, noise generated by power transformer was predominantly load current. Input and output data, serving as targets, have a large variation in
values. This variation can be overcome by changing data input such as power, impedance, and the weight of the
winding in the form of logarithmic functions in dB, as shown in Table 1. Based on the analysis, load noise data are obtained from short
circuit testing, while other parameters are collected from power transformer design data.
Table 1 Data of input parameters
2.3.
Development of Load Noise Model
The development of load noise model was carried out using two methods, namely multiple
linear regression (MLR) and BPNN.
2.3.1. MLR Method
MLR is a statistical method that simulates the
relationship between two or more independent variables and a dependent variable
through a relationship in the form of a linear equation (Rinanto
and Kuo, 2021). The form of MLR
equation used in this research is showed by Equation (1). The output variable is a function of input variable
and a random error
added to
develop a probabilistic model rather than deterministic. Subsequently, the coefficient
usually unknown, are
estimated, where
is a
dependent variable,
is an
intercept for regression equations,
is the
coefficients of independent variable
is an error
between the measurement and the prediction result. Equation (1) can be written as Equation (2).
where is the
matrix of dependent variables,
is the input
matrix, and
is the error
matrix. To obtain the coefficient
value of each independent
variable, the error value is made minimum with the least square method.
Equations (2) and (3) are used to obtain the
coefficient of independent variable. Finally,
MLR equation can be written as Equation (4), where
is the MLR model's output and
is the matrix transpose of
Optimum MLR was determined based on statistical performance criteria. These criteria included the coefficient
of multiple determinationsadjusted
coefficient of multiple determination
and prediction
coefficient of multiple determination
2.3.2. Artificial Neural Network (ANN) Method
The structure of ANN consists of input, hidden layer, and
output. Among
ANN architectures, network with MLP structures are very commonly
used to model system (Sholahudina
and Han, 2015). ANN architectures consist of three or more layers, namely the input, hidden, and output, with each neuron interconnected
with a set weight. The determination of neurons in each layer lacks standard rules and varies based on the specific problem to be solved (Najemalden,
Ibrahim, and Ahmed, 2020;
Dhini et al., 2015). Currently, there is no mathematical method capable of determining the exact number of hidden layers and neuron
elements. According to (Haykin,
2008), it was suggested to start
training on an ANN using a small number of hidden and increased neurons to obtain a satisfactory mean square error
(MSE) value. Although no definite mathematical equation for the number of
hidden layers and neurons, the theory by Kolmogorov as expressed in Eq. (5) has been proven effective (Wang
et al., 2021).
is the
number of neurons in the hidden and input layers.
ANN uses a
supervised training method because the input and target have been known. Therefore, knowledge and
appropriate input selection are needed during modeling with ANN (Munakata,
2007). Training ANN is a mathematical
exercise that optimizes all weight and threshold values using fractions of the
available data. Neural network provide empirical model of a complex system capable of unraveling the underlying relationships and
completely understanding the system (Dhini
et al., 2015). In this research, the relationship between the input
signal and the output is expressed
by Equation (6).
where is the weight of the relationship,
is the bias value.
ANN with hidden layer and adequate units has the capability to
theoretically
method a non-linear relationship model.
The mathematical relationship between input X and output Y can be established
by adjusting the weight of the matrix W as well as bias vector B in the hidden and output layers
to minimize the MSE during the training process. This adjustment of network parameter values occurs iteratively during the training or learning phase. After training, network is tested with a signal transmitted forward from input to
output. The output result
is
compared with the target
to
obtain the error, followed by evaluation of model performance using the
determination coefficient (R), and the
value of MSE. When the error obtained does not meet the
required criteria, network parameters are recalculated. The correction of parameters
is carried out in the backward direction and network
trained are called backpropagation network. During the training process, the transmission of a single signal from the start to backpropagation of the
error is called the epoch. The iteration process continues until one of the
stopping criteria is met through many epochs or errors. Although
various learning methods have been developed, this research uses Levenberg-Marquardt optimization.
2.4.
Prediction Performance Criteria
The
determination
of the best model was carried out by testing with the same data and
selecting the optimal criteria.
The best model was identified based on the smallest root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and the largest determination coefficient
(R). Subsequently, Equations (7) to (10) were used to measure model's performance.
3.1. MLR Model
Based on Table 2, with as independent parameters and load
noise as dependent, the initial step is to select the best model among the independent parameters. Table 2 shows the possibility of MLR model with various parameter combinations.
Since
is significantly influenced by the number of parameters, there is
a need to use other criteria for
determining the best model. In this
research,
was used to combine the number of parameters affecting dependency. Specifically,
value provides
information on how well model can predict with new data, indicating that higher
shows a
better model for predicting load noise.
Table 2 Possibility of MLR model with various parameters
The results showed that model with two parameters, namely log (S) and log (Z) produced the best results, as indicated by Based on Equations (1) to (4), load noise
model was obtained in the form of MLR equation, as expressed in Equation (11) :
The comparison between
MLR method and the measurement results is shown in Figure 2(a), presenting the
maximum and minimum deviations of 7.41 dB and -8.62 dB, respectively, with a
MAPE, MAE, RMSE, and R in a row 0.039, 2.727, 3.649 and 0.917.
3.2. BPNN Model
According to (Wang et al., 2021), the number of neurons in each hidden layer can be
determined by Equation (5). Since there are four input
parameters, number of neurons in each hidden layer is nine. However, there are no exact rules or equations to determine the appropriate number of hidden
layers for load noise model. Therefore, number of hidden layers in load noise
model is carried out by trial and error, from the smallest number until the best results are
achieved (Sadighi, Mohaddecy, and Abbasi, 2018).
In this research, the appropriate number
of hidden layers is selected based on the MSE and R values of
each test performed. According to the search results in Table 3, several hidden layers did not always give the
best results. Therefore, seven hidden layers were selected with MSE and R values
of 0.271 and 0.998, respectively. Figure 1 shows the BPNN structure that has the best results
with seven hidden layers, each consisting of nine neurons. Figure 1 The structure of BPNN for load noise model
Table 3 Comparison of trained network for load noise model
|
No. of
hidden layer |
Hidden
transfer function |
MSE |
R |
|
4×9×9×1 |
Logsig, Logsig |
65.38 |
0.589 |
|
4×9×9×9×1 |
Logsig, Logsig, Logsig |
46.17 |
0.748 |
|
4×9×9×9×9×1 |
Logsig, Logsig, Logsig, Logsig |
48.32 |
0.790 |
|
4×9×9×9×9×9×1 |
Logsig, Logsig, Logsig, Logsig, Tansig |
0.877 |
0.996 |
|
4×9×9×9×9×9×9×1 |
Logsig, Logsig, Logsig, Logsig, Logsig,
Logsig |
70.83 |
0.479 |
|
4×9×9×9×9×9×9×9×1 |
Logsig, Logsig, Logsig, Logsig, Logsig,
Logsig, Tansig |
0.271 |
0.998 |
The bold values are selected as model with the optimum structure.
Figure 2 Comparison of load noise between measurement and the other method
The
accuracy of model was evaluated
by comparing the measurement results, the Reiplinger method, and load noise
calculated at the design stage of the industry. Figure 2(b) shows that the Reiplinger method has a large deviation compared to
the measurement results. Based on the results, the maximum
and minimum deviations were 9.96 dB and -6.14 dB, with MAPE, MAE, RMSE, and R in row 0.058, 4.285, 5.199, and 0.894,
respectively. Meanwhile, Figure 2(c) shows the results of
calculations carried out at the industrial design stage, which obtained the maximum and minimum deviation values of 9.24 dB and -6.62 dB, with a MAPE, MAE,
RMSE, and R in a row 0.057, 4.049, 4.942, and 0.900, respectively.
Load noise model developed by BPNN method has the smallest deviation from
the measurement results compared to others. The maximum and minimum deviations
are 1.25 dB and -1.69 dB, with a MAPE, MAE,
RMSE, and R in a row 0.007, 0.464, 0.708, and 0.998, respectively. These performance criteria showed that the development of load noise model with BPNN provided
better accuracy. The comparison results in Figure 2(d) showed that BPNN could be developed for predicting load noise at the early design stage of power transformer.
Figure 3 shows a comparison
of each performance criterion, where BPNN model produces the best results. Specifically, Figure 3(a) shows that the MAPE for BPNN model has the
lowest value of 0.7% compared to others. The low
MAE, as presented in Figure 3(b), shows that BPNN model can
forecast load noise compared to others. The low RMSE, shown in Figure 3(c), indicates that the variation in predicted value is close to BPNN
observational value. The R-value presented in Figure 3(d) shows the strong
correlation between independent and dependent variables. Statistically,
Table 4 shows a summary
of the three models tested, with BPNN producing the best results compared
to others.
Figure 3 Statistical performance comparison
of each model
Table 4 Summary of comparisons of all
models
|
Performance
criteria |
BPNN method |
Design calc. |
Reiplinger method |
MLR method |
|
MAPE |
0.007 |
0.057 |
0.058 |
0,039 |
|
MAE |
0.464 |
4.049 |
4.285 |
2.727 |
|
RMSE |
0.708 |
4.942 |
5.199 |
3.649 |
|
R |
0.998 |
0.900 |
0.894 |
0.917 |
In conclusion, this research successfully developed load noise model using BPNN. Based on the results, the optimal structure of BPNN for power transformer load
noise model with power, impedance, and WGF as inputs was found to be 4-9-9-9-9-9-9-9-1, with MAPE, MAE, RMSE, and R values of 0.007, 0.464,
0.708 and 0.998, respectively. This model should potential to predict load noise for power transformer without using detailed design
data. The prediction of load noise with BPNN produced high accuracy compared to the existing standard formulas. Therefore, load noise model obtained in this research could be implemented for further investigation to design a low-load noise power transformer.
The authors are grateful for the
financial support received from PT Elsewedy Electric Indonesia and RTA (Final
Project Recognition, contract number 2448/UN1.P.III/DIT-LIT/PT/2020) program
from Gadjah Mada University, Yogyakarta.
Al-Abadi, A., Gamil, A., Schatzl, F., Vander, B., Groot,
E.D., Declercq, J., 2017. Investigating The Effect of Winding Design and
Clamping Pressure on Load-Noise Generation of Power Transformer. In:
CIGRE Study Committee A2 Colloqium, pp. 1-10
Al-Abadi, A., 2019. Developing an Accurate Load Noise Formula
for Power Transformers. In: 2019 6th International Advanced
Research Workshop on Transformers (ARWtr), January, pp. 19–24
Alas, M., Ali, S.I.A., 2019. Prediction of
the High-Temperature Performance of a Geopolymer Modified Asphalt Binder using
Artificial Neural Networks. International Journal of Technology, Volume
10(2), pp. 417–427
Aziz, M., Indarto, A., Hudaya, C.,
2021. Study of Material Characteristics of Core and Winding to Minimize Losses
on Power Transformer. IOP Conference Series: Earth and Environmental Science,
Volume 673(1), p. 012008
Dhini, A., Faqih, A., Kusumoputro, B., Surjandari, I.,
Kusiak, A., 2020. Data-driven Fault Diagnosis of Power Transformers using
Dissolved Gas Analysis (DGA). International Journal of Technology,
Volume 11(2), pp. 388–399
Dhini, A., Surjandari, I., Riefqi, M., Puspasari, M.A., 2015.
Forecasting Analysis of Consumer Goods Demand using Neural Networks and
ARIMA. International Journal of Technology, Volume 6(5),
pp. 872–880
Duan, X., Zhao, T., Liu, J., Zhang, L., Zou, L., 2018.
Analysis of Winding Vibration Characteristics of Power Transformers Based on
the Finite-Element Method. Energies, 11(9), p. 2404
Fagbola, T.M., Thakur, C.S., Olugbara, O., 2019. News Article
Classification using Kolmogorov Complexity Distance Measure and Artificial
Neural Network. International Journal of Technology, Volume 10(4), pp. 710–720
Girgis, R.S., Bernesjö, M., Anger, J., 2009. Comprehensive
Analysis of Load Noise of Power Transformers. In: 2009 IEEE Power and
Energy Society General Meeting, PES ’09, pp. 1–7
Haykin, S., 2008. Neural Networks and Learning Machines.
3rd ed. Pearson Prentice Hall
Indarto, A., Garniwa, I., Setiabudy, R., Hudaya, C., 2017.
Total cost of ownership analysis of 60 MVA 150/120 kV Power Transformer. In:
2017 15th International Conference on Quality in Research (QiR)
2017, pp. 291–295
Jin, M., Pan, J., 2016. Vibration Characteristics of a
Disk-Type Winding Simulated by Coupled Concentric Rings. Applied Acoustics,
Volume 101, pp. 104-114
Jingzhu, H., Dichen, L., Oingfen, L., Yang, Y., Shanshan, L.,
2016 Electromagnetic Vibration Noise Analysis of Transformer Windings and Core.
IET Electric Power Applications, Volume 10(4), pp. 251-257
Kim, D.K., Ryu, J.Y., Kim, D.M., Kim, D.J., Lim, M.S., 2020.
Load Noise Prediction of High-Voltage Transformers by Equation Applying 3-D
EMCN. IEEE Access, Volume 8, pp. 130669–130677
Lukic, L., Djapic, M., Lukic, D., Petrovic, A., 2012. Aspects
of Design of Power Transformers for Noise Reduction. In: International
Conference Noise and Vibration, pp. 255–262
Munakata, T., 2007. Fundamentals of the New Artificial
Intelligence. Lodon: Springer
Najemalden, A.M., Ibrahim, S.W., Ahmed, M.D., 2020.
Prediction of Collapse Potential for Gypseous Sandy Soil Using ANN Technique. Journal
of Engineering Science and Technology, Volume 15(2), pp. 1236–1253
Negi, R., Singh, P., Shah, G.K., 2013. Causes of Noise
Generation and Its Mitigation in Transformer. International Journal of
Research in Electrical and Instrumentation Engineering, Volume 2(5), pp.
1732-1736
Paghadar, H., Kantaria, R.A., 2016. Accurate
Estimation and mitigation of Audible Sound using Novel Technique of Flux
Density Reduction at Design Stage in Transformer. International Journal of
Electrical and Electronics Engineering, Volume 3(10), pp. 12–15
Pramono, W.B., Hadi, S.P., Wijaya, F.D., Nugroho, H.A.,
Wibirama, S., 2020. Study of Power Transformer Noise Prediction. In:
2020 7th International Conference on Information Technology,
Computer, and Electrical Engineering (ICITACEE), pp. 213–218
Pramono, W.B., Wijaya, F.D., Hadi, S.P., 2021. Prediction
Formula Development of Power Transformer No-Load Noise. Journal of Physics:
Conference Series, Volume 1858(1), p. 012014
Pramono, W.B., Wijaya, F.D., Hadi, S.P., Indarto, A.,
Wahyudi, M.S., 2023. Application of a PCA-MLR Load Noise Prediction Model for
The Power Transformer. In: 2023 7th International Conference
on Electrical, Telecommunication and Computer Engineering (ELTICOM), pp.
188-193
Rinanto, N., Kuo, C.H., 2021. PCA-ANN
Contactless Multimodality Sensors for Body Temperature Estimation. IEEE
Transactions on Instrumentation and Measurement, Volume 70, pp. 1–16
Rohilla, V., Samy, C.P., 2015. A Study of Transformer Noise
and Reduction Techniques of Transformer Noise. Journal of Basic and Applied
Engineering Research, Volume 2(22), pp. 1911-1915
Rozhentcova, N., Galyautdinova, A., Khayaliev, R., Udaratin,
A.V., Ilyashenko, S., 2020. Automated Diagnostic System for Power Transformers
using a QR Code. International Journal of Technology, Volume 11(8), pp.
1519–1527
Sadighi, S., Mohaddecy, S.R.S., Abbasi, A., 2018. Modeling
and Optimizing a Vacuum Gas Oil Hydrocracking Plant using an Artificial Neural
Network. International Journal of Technology, Volume 9(1), pp. 99–109
Sathya, A., Savadamuthu, U., 2019. Electromagnetic Force and
Deformation in Transformer Winding. International Journal of Applied
Engineering Research, Volume 14(3), pp. 790–796
Shilyashki, G., Pfutzner, H., Hamberger, P., Aigner, M.,
Kenov, A., Matkovic, I., 2016. Spatial Distributions of Magnetostriction,
Displacements and Noise Generation of Model Transformer Cores. International
Journal of Mechanical Sciences, Volume 118, pp. 188-194
Sholahudin, S., Han, H., 2015. Heating Load Predictions using
The Static Neural Networks Method. International Journal of Technology,
Volume 6(6), pp. 946953
Vasques, C.M.A., Miguel, H., Campelo, R., 2013. Quiet
Transformers?: Design Issues. Advanced Research Workshop on Transformers,
pp. 1–17
Wang, Z., Wei, W., Langari, R., Zhang, Q., Yan, Q., 2021. A
Prediction Model Based on Artificial Neural Network for the Temperature
Performance of a Hydrodynamic Retarder in Constant-Torque Braking Process. IEEE
Access, Volume 9, pp. 24872–24883.
Witczak, P., Swiatkowski, M., 2017. Modelling Axial Vibration
in Windings of Power Transformers. Journal Open Physics, Volume 15(1),
pp. 862-866
Yoshida, K., Hoshino, T., Murase, S., Murakami, H.,
Miyashita, T., 2021. Analysis of Load Noise Components in Small Core-Form
Transformers. IEEE Transactions on Power Delivery, Volume 36(5), pp.
2694–2704
Yu, X.C., Zou, D.P., Fan, M.Z., Dong, X., Du, F., 2022.
Vibration and Noise Suppression Method of Transformer. Journal of Physics:
Conference Series, 2158 012030
Zhu, L., Hao, J., Lu, L., 2022. Research on Influence of
Damping on the Vibration Noise of Transformer. IEEE Access, Volume 10,
pp. 92128–92136
