• International Journal of Technology (IJTech)
  • Vol 13, No 3 (2022)

An Empirical Model for Optimizing the Sound Absorption of Single Layer MPP Based on Response Surface Methodology

An Empirical Model for Optimizing the Sound Absorption of Single Layer MPP Based on Response Surface Methodology

Title: An Empirical Model for Optimizing the Sound Absorption of Single Layer MPP Based on Response Surface Methodology
Al-Ameri Esraa, Azma putra, Ali Mosa, Reduan M Dan, Osam H Attia

Corresponding email:


Published at : 01 Jul 2022
Volume : IJtech Vol 13, No 3 (2022)
DOI : https://doi.org/10.14716/ijtech.v13i3.5507

Cite this article as:
Esraa, A., Putra, A., Mosa, A., Dan, R.M., Attia, O.H., 2022. An Empirical Model for Optimizing the Sound Absorption of Single Layer MPP Based on Response Surface Methodology. International Journal of Technology. Volume 13(3), pp. 496-507

780
Downloads
Al-Ameri Esraa Fakulti Kejuruteraan Mekanikal, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, 76100 Durian Tunggal, Melaka, Malaysia
Azma putra Centre for Advanced Research on Energy, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, 76100 Durian Tunggal, Melaka, Malaysia
Ali Mosa Department of Mechanical Engineering, Collage of Engineering, University of Baghdad, Jadriyah - Baghdad, Iraq
Reduan M Dan Centre for Advanced Research on Energy, Universiti Teknikal Malaysia Melaka, Hang Tuah Jaya, 76100 Durian Tunggal, Melaka, Malaysia
Osam H Attia Department of Reconstruction and Projects, University of Baghdad, Jadriyah - Baghdad, Iraq
Email to Corresponding Author
Abstract
An Empirical Model for Optimizing the Sound Absorption of Single Layer MPP Based on Response Surface Methodology

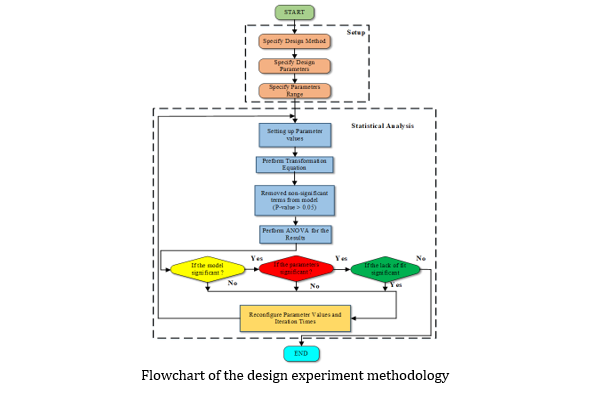
Micro-perforated panel (MPP) is a thin panel absorber capable of absorbing sound energy at a targeted frequency range by adjusting the MPP parameters. An analytical model is available, but it is not a direct, convenient method for practitioners to determine the required MPP parameters. This paper presents an optimized empirical model to calculate the sound absorption coefficient of a single-layer MPP.  The response surface methodology is employed for a simple case to generate a second-order polynomial model through a sequence of designing processes to analyze the functional relationships and variation of the outcome performance (sound absorption coefficient) concerning the MPP parameters, namely the panel thickness, hole diameter, perforation ratio, and the depth of the back air layer.  The analysis is carried out for frequencies between 300 to 900 Hz. The predicted data (empirical) is compared with the actual data (analytical), leading to a coefficient of variation of 0.145%. The proposed empirical model can be used as a method to select the suitable MPP parameters according to the targeted frequency bandwidth of absorption with less computational time.

Optimisation; Response Surface Methodology (RSM); Single layer MPP; Sound absorption

Introduction

    The Microperforated panel (MPP) absorber proposed by Maa (1975) has been widely used as a next-generation sound absorbers system (Mosa et al., 2018). It has the advantages of providing a high sound absorption coefficient, ease of installation, fine washability, environmental friendliness, and attractive appearance (Tayong et al., 2018; Yang et al., 2019), as an alternative to porous absorbing materials  (Ahmad & Salih, 2020; Prasetiyo et al., 2020). Aimed for a wide absorption bandwidth; many studies have been presented on a single layer MPP using various techniques. This includes the presents of the MPP model with incompletely partitioned cavities (Huang et al., 2017) broadband MPP model with ultra-MPP (Qian et al., 2014a); thin MPP models (Prasetiyo et al., 2021), inhomogeneous MPP systems with multiple cavity depths (Prasetiyo et al., 2016; Mosa et al., 2019; Kusaka et al., 2021).
    The analysis and optimization of the MPP parameters to enhance the absorption performance have been presented (Qian et al., 2014b; Yu et al., 2016); however, most of these processes are consumed time with convoluted processing steps, especially models of a large structure (Hussein, 2020; El-Basheer et al., 2017). Generally, it should be considered that the potential interactions between model variables could cause incorrect optimum parameters as any modifying parameter at a time. In order to minimize these computational efforts, the approach of the response surface methodology (RSM) has been employed to implement the optimization of the acoustic absorption for numerous noise control applications (Liang et al, 2007; Harahap et al., 2019; Wang et al., 2017; Wahab et al., 2019).
    Box and Wilson (1951) first presented this method to initialize and evolve empirical models and by providing the basic principles framework of RSM, they denote the response process. Randall P. and Terence J. (Niedz & Evens, 2016) attained a review discussing the theoretical aspects and practical applications of RSM literature. Essentially, the RSM involves replacing the complete procedure along with an empirical model by collecting a series of results at several detached points within the design domain. The impression of the second-order functions is because of the low-order processes are powerful, since generating the corresponding response surface is fast and cheap. (Boulandet & Lissek, 2010; Hawashi et al., 2019; Petrus et al., 2021; Saleh et al., 2021).
    Even though several studies have been presented on the absorption performance of MPP using analytical or simulation methods. Still, they are not direct, convenient methods for practitioners to determine the required MPP parameters. Thus, the current study uses a factorial design of experiment software to present a novel empirical model for a single-layer-MPP absorber based on RSM to contribute a straightforward and more accessible model with less computational time. Furthermore, to optimize the relationship between the model parameters (holes diameters and ratio, cavity depth, and panel thickness). The paper structure presents recent studies on the MPP and the RSM, followed by the empirical model theories and generation methodology step. Section 3 summarized the model validation and predicted results. The conclusion of the study is present at the end.

Conclusion

    The optimized empirical model to calculate the sound absorption coefficient of a ?single-layer MPP has been presented in this paper. The model was developed using the response? surface methodology to generate a second-order polynomial model as a function of MPP parameters, namely the hole diameter, the perforation ratio and the depth of the back air layer?. The predicted data is evaluated with the actual data leading to a coefficient of variation ?of about 0.145%. The predicted model is then verified with the analytical model with good agreement. The proposed model in this paper is however, only valid for the frequency range of 300 – 900 Hz. The same method can be used to generate empirical models of a single layer MPP with a different frequency range of interest. In future work, these empirical models can be utilized as the complete set of mathematical tools to calculate the absorption coefficient of MPP conveniently. The work can also be extended with the more complicated configuration of the MPP structure, such as the double-leaf MPP and the multi-cavity MPP.

Acknowledgement

    The authors would like to express their gratitude to Universiti Teknikal Malaysia Melaka (UTeM). Part of this project is supported by the Fundamental Research Grant Scheme ?from the Ministry of Higher Education Malaysia No. FRGS/1/2016/ ?TK03/FTK­CARE/F00323?. The corresponding author would like to express appreciation for the University of Baghdad for its great support.

References

Ahmad, S.H,  Salih, R.M., 2020. Acoustic and Thermal Insulation of Nanocomposites for Building Material. Baghdad Science Journal, Volume 17 (2), pp. 494–501

Bimakr, M., Ganjloo, A., Noroozi, A., 2019. Effect of Acoustic Cavitation Phenomenon on Bioactive Compounds Release from Eryngium Caucasicum Leaves. Journal of Food Measurement and Characterization 13 (3), Volume, pp. 1839–1851

Boulandet, R., Lissek, H., 2010. Optimization of Electroacoustic Absorbers by Means of Designed Experiments. Applied Acoustics, Volume 71 (9), pp. 830–842

Box, G. E. P., & Wilson, K. B., 1951. On the Experimental Attainment of Optimum Conditions. Journal of the Royal Statistical Society, Volume 13(1), pp. 1–38

Bucciarelli, F., Fierro, G.P.M., Meo, M., 2019. A Multilayer Microperforated Panel Prototype for Broadband Sound Absorption at Low Frequencies. Applied Acoustics, Volume 146, pp. 134–144

Deeying, J., Asawarungsaengkul, K., Chutima, P., 2018. Multi-Objective Optimization on Laser Solder Jet Bonding Process in Head Gimbal Assembly using the Response Surface Methodology. Optics and Laser Technology, Volume 98, pp. 158–168

El-Basheer, T.M., Youssef, R.S., Mohamed, H.K., 2017. NIS Method for Uncertainty Estimation of Airborne Sound Insulation Measurement in Field. International Journal of Metrology and Quality Engineering, Volume 8, p. 19

Harahap, A.F.P., Rahman, A.A., Sadrina, I.N., Gozan, M., 2019. Optimization of Pretreatment Conditions for Microwave-assisted Alkaline Delignification of Empty Fruit Bunch by Response Surface Methodology. International Journal of Technology, Volume 10(8), pp. 1479–1487

Hawashi, M., Aparamarta, H., Widjaja, T., Gunawan, S., 2019. Optimization of Solid State Fermentation Conditions for Cyanide Content Reduction in Cassava Leaves using response surface methodology. International Journal of Technology, Volume 10(3), pp. 624–633

Huang, S., Li, S., Wang, X., Mao, D., 2017. Micro-Perforated Absorbers with Incompletely Partitioned Cavities. Applied Acoustics, Volume 126, pp. 114–119

Hussein, T.M.E.-B., 2020. Calibration and Uncertainty Estimation for the Reference Sound Source in Reverberation Room. Romanian Journal of Acoustics and Vibration, Volume 17(2), pp. 118–127

Kusaka, M., Sakagami, K., Okuzono, T., 2021. A Basic Study on the Absorption Properties and Their Prediction of Heterogeneous Micro-Perforated Panels: A Case Study of Micro-Perforated Panels with Heterogeneous Hole Size and Perforation Ratio. Acoustics, Volume 3(3), pp. 473–484

Liang, X., Lin, Z., Zhu, P., 2007. Acoustic Analysis of Damping Structure with Response Surface Method. Applied Acoustics, Volume 68 (9), pp. 1036–1053

Liu, Z., Zhan, J., Fard, M., and Davy, J.L., 2017. Acoustic Properties of Multilayer Sound Absorbers with a 3D Printed Micro-perforated Panel. Applied Acoustics, Volume 121, pp. 25–32

Maa, D.Y., 1975. Theory and Design of Microperforated Panel Sound-Absorbing Constructions. Scientia Sinica, Volume 18(1), pp. 55–71

Maa, D.Y., 1987. Microperforated-Panel Wideband Absorbers. Noise Control Engineering Journal, Volume 29(3), pp. 77–84

Mosa, A.I., Putra, A., Ramlan, R., Esraa, A.-A., 2018. Micro-Perforated Panel Absorber Arrangement Technique: A Review. Journal of Advanced Research in Dynamical and Control Systems, Volume 10(7): 372–381

Mosa, A.I., Putra, A., Ramlan, R., Prasetiyo, I., Esraa, A.-A., 2019. Theoretical Model of Absorption Coefficient of an Inhomogeneous MPP Absorber with Multi-Cavity Depths. Applied Acoustics, Volume 146, pp. 409–419

Niedz, R.P., Evens, T.J., 2016. Design of Experiments (DOE)-History, Concepts, and Relevance to in Vitro Culture. In Vitro Cellular and Developmental Biology - Plant, Volume 52 (6), pp. 547–562

Petrus, H.T.B.M., Olvianas, M., Astuti, W., Nurpratama, M.I., 2021. Valorization of Geothermal Silica and Natural Bentonite through Geopolymerization: A Characterization Study and Response Surface Design. International Journal of Technology, Volume 12(1), pp.196–206

Prasetiyo, I., Muqowi, E., Putra, A., Novenbrianty, M., Desendra, G., Adhika, D.R., 2020. Modelling Sound Absorption of Tunable Double Layer Woven Fabrics. Applied Acoustics, Volume 157, p. 107008

Prasetiyo, I., Sarwono, J., Sihar, I., 2016. Study on Inhomogeneous Perforation Thick Micro-Perforated Panel Sound Absorbers. Journal of Mechanical Engineering and Sciences (JMES), Volume 10(3), pp. 2350–2362

 Prasetiyo, I., Sihar, I., Sudarsono, A.S., 2021. Realization of a Thin and Broadband Microperforated Panel (MPP) Sound Absorber. Applied Acoustics, Volume 183, p. 108295

Qian, Y.J., Cui, K., Liu, S.M., Li, Z.B., Kong, D.Y., Sun, S.M., 2014a. Development of Broadband Ultra Micro-Perforated Panels Based on MEMS Technology. Applied Mechanics and Materials, Volume 535, pp. 788–795

Qian, Y.J., Cui, K., Liu, S.M., Li, Z.B., Shao, D.S., Kong, D.Y., Sun, S.M., 2014b. Optimization of Multi-Size Micro-Perforated Panel Absorbers using Multi-Population Genetic Algorithm. Noise Control Engineering Journal, Volume 62(1), pp. 37–46

Saleh, B.J., Saedi, A.Y.F., Al-Aqbi, A.T.Q., Salman, L.A., 2021. Optimum Median Filter Based on Crow Optimisation Algorithm. Baghdad Science Journal, Volume 18(3), pp. 614–627

Tayong, R.B., Jacques, A., Manyo, M., Siryabe, E., Ntamack, G.E., 2018., On the Simultaneous Inversion of Micro-Perforated Panels’ Parameters: Application to Single and Double Air-Cavity Backed Systems. The Journal of the Acoustical Society of America, Volume 143(4), pp. 2279–2288

Wahab, H.A., Rus, A.ZM., Abdullah, M.F.L., Abdullah, N.M., 2019. Design of Experiment for Sound Absorption Materials of Microporous Polymer. In: International Conference on Information Science and Communication Technology (ICISCT) 2019, pp. 1–7

Wang, Y., Qin, X., Huang, S., Lu, L., Zhang, Q., Feng, J., 2017. Structural-Borne Acoustics Analysis and Multi-Objective Optimization by using Panel Acoustic Participation and Response Surface Methodology. Applied Acoustics, Volume 116, pp. 139–151

Wyantuti, S., Setyorini, Z., Ishmayana, S., Hartati, Y., Firdaus, M., 2020. Optimisation of Voltammetric Determination of Dysprosium (III) using Plackett-Burman and RSM-CCD Experimental Designs. Baghdad Science Journal, Volume 17(4), pp. 1198–1206

Yang, X., Bai, P., Shen, X., To, S., Chen, L., Zhang, X., Yin, Q., 2019. Optimal Design and Experimental Validation of Sound Absorbing Multilayer Microperforated Panel with Constraint Conditions. Applied Acoustics, Volume 146, pp. 334–344

Yu, X., Cui, F.S., Cheng, L., 2016. On the Acoustic Analysis and Optimization of Ducted Ventilation Systems using a Sub-Structuring Approach. The Journal of the Acoustical Society of America, Volume 139 (1), pp. 279–289

Download PDF
Who cite this paper
Table of Contents
Article
Abstract
Introduction
Conclusion
Acknowlegement
References