Numerical Study on Relocation Process of Al, Fe, and Pb by Using the Moving Particle Semi-Implicit Method During Severe Accident of Reactor
Published at : 28 Jun 2023
Volume : IJtech
Vol 14, No 4 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i4.5240
Yulianto, Y., Mustari, A.P.A., 2023. Numerical Study on Relocation Process of Al, Fe, and Pb by Using the Moving Particle Semi-Implicit Method During Severe Accident of Reactor. International Journal of Technology. Volume 14(4), pp. 800-810
| Yacobus Yulianto | Physics Department, Halu Oleo University, Jl. H.E.A. Mokodompit, Kendari 93232, Indonesia |
| Asril Pramutadi Andi Mustari | Physics Department, Bandung Institute of Technology, Jl. Ganesha 10, Bandung 40132, Indonesia |
Reactor safety is one of the essential parts of
reactor research, especially to appropriately respond when melts down occurred
during a severe accident. In this study, the relocation process of Al, Fe, and
Pb was simulated by using the Moving Particle Semi-Implicit method to study the
relocation mechanism of the liquids when they experienced an interaction
between liquids at high temperatures. It is obtained that, to reach the
stratified condition, Pb-Al needs 0.63 seconds, Al-Fe and Al-Pb need 1.14
seconds, and Fe-Al needs more than three seconds. Overall, the results indicate
that the difference in viscosity and density between two liquids influences the
time to reach the stratified condition. The greater the density difference
between two liquids, the faster the stratification process.
Liquid flow; Moving particle semi-implicit; Relocation process; Severe accident of a reactor
Reactor safety is one of the substantial
matters that should be concerned in the study of the reactor. The reactor
accidents of Three Miles Island, Chernobyl, and Fukushima have warned nuclear
researchers to care about the importance of reactor safety. Information about
the behavior of some reactor materials (Talaat et al., 2019; Chandran
et al., 2018) is very urgent to be provided.
The relocation of melting material during a severe accident is an important
phenomenon due to its influence on the heat transfer to the lower plenum of the
reactor, which may affect the breaching of the reactor.
Several
studies have been conducted regarding the relocation of molten corium.
Moreover, stratification during the accident is also important to be understood
to predict the failure of the reactor pressure vessel (Li et al., 2013). During a severe accident, the variation of
materials may lead to several combinations of interaction between two materials.
In the research reactor, Fe-Al interaction may need to be understood since Al
is the main material with parts of Fe (Hainoun, Ghazi, and Alhabit, 2019; Farrell, 2012). On the other hand, in the LFR (Lead-cooled
Fast Reactor), a study of Pb-Fe interaction in the liquid phase is needed. The
reason is that Pb is the main coolant and Fe is the main structural material (Mustari and
Takahashi, 2011; Machut et al., 2007), where Al is proposed as the
outer layer of structural material (Knebel et al., 2000) in the Accelerator Driven System
(ADS). Unfortunately, investigations on these material combinations in the
liquid phase are very limited.
Some experiments about reactor core
accidents are complicated or costly to be performed. Although experiments are
still principal for some cases, computational simulations (Aliffrananda et
al., 2022; Utama et al., 2021) can be an alternative to reduce
the complexity or the cost of experiments. On the other hand, the conventional
mesh methods face difficulty in explaining several melted core phenomena, i.e.
stratification case, free-surface flow, and phase transitions. The Moving
Particle Semi-Implicit (MPS) method introduced first by Koshizuka and Oka (1996) is one of the alternative mesh-free methods
utilized to simulate the relocation process of some nuclear materials. This
method has been applied successfully (Duan, Yamaji, and Sakai, 2022; Masumura, Yamaji, and Furuya 2015; Mustari et al., 2015; Li, Oka, and Furuya, 2014; Kawahara and Oka, 2012) as reviewed by Li et al. (2020).
While there are many studies analyzing
melting interactions between the melted core and solid materials during reactor
core melting, there is still limited simulation on the relocation of molten
fluids. Studies of the relocation process of some liquids were performed by
some researchers, such as Li et al. (2013) with silicon oil and salt water, Ilham et al. (2018) with freshwater, and Hidayati et al. (2021) with cooking oil and freshwater. In this
study, the liquids of Al, Fe, and Pb are utilized. The simulation of the
relocation process is one of the visible solutions for understanding the
phenomena in the reactor accident. Therefore, the study of the relocation
process is utterly substantial to be performed for nuclear materials. Due to
the lack of study on the materials in the case of a severe accident, where most
materials are in the liquid phase, the objective of this study is to simulate
the relocation process of some liquids of nuclear materials (Al, Fe, and Pb)
and the contact process between two liquids with various temperatures.
2.1. Mathematical Model and Numerical Method
The
Moving Particle Semi-Implicit method assumes that a particle only exercises an
interaction with a limited number of its nearest particles as shown in Figure
1. To
accommodating this assumption, the weight function exists as described well in
the paper of Koshizuka and Oka (1996),
including the explanation of the particle number density, the gradient, the
divergence, and the Laplacian models. All equations in the MPS method follow
the mass and the momentum conservation equations as the commonly used governing
equations for incompressible flow where (Koshizuka
and Oka, 1996).
the time is represented by t, the velocity vector is
represented by 
the gradient is represented by 
the gravity is represented by
the pressure is represented by P, and the
kinematic viscosity is represented by 
To assist the calculation process, the numerical
calculations are proceeded explicitly by using the finite difference method and
implicitly by using the Crank-Nicholson method (Koshizuka
and Oka, 1996). Here are the
references that explained the MPS method clearly, including the algorithm (Li
et al., 2020; Kawahara and Oka, 2012; Koshizuka and Oka, 1996).2.2. Simulation
In
this study, two types of liquids were used, namely, the fallen liquid placed
inside the 2D containment and the target liquid placed inside a bottle located
102 mm above the surface of the target liquid. Both liquids are chemically
miscible, and it was assumed that the stratification process in
thermal-hydraulic is faster than in the chemical process, as supported by
references (Mustari
et al., 2015; Mustari and Oka, 2014), these liquids can be considered as an immiscible
liquid. The temperature, density, and kinematic viscosity of each used liquid
can be seen in Table 1. The simulation was performed by using 4139
particles and a similar code of these references (Yulianto et al., 2019; Ilham et al.,
2018).
Figure 1 Boundary (a) and initial (b)
condition (in mm)
Table 1 The parameters of each
liquid (IAEA, 2008)
|
Component |
Tmelting (°C) |
Tboiling (°C) |
Tsimulation
(°C) |
Density (kg m-3) |
Kinematic viscosity (m2
s-1) |
|
Al |
660 |
2,519 |
1,600 |
2.084890 × 103 |
7.382931 × 10-4 |
|
1,800 |
2.022690 × 103 |
7.083604 × 10-4 | |||
|
2,000 |
1.960490 × 103 |
6.846094 × 10-4 | |||
|
Fe |
1,538 |
2,861 |
1,600 |
6.977548 × 103 |
2.050208 × 10-3 |
|
1,800 |
5.115362 × 103 |
1.784475 × 10-3 | |||
|
2,000 |
4.930162 × 103 |
1.591594 × 10-3 | |||
|
Al |
660 |
2,519 |
1,200 |
2.209290 × 103 |
8.295089
× 10-4 |
|
1,400 |
2.147090 × 103 |
7.771429
× 10-4 | |||
|
1,600 |
2.084890 × 103 |
7.382931
× 10-4 | |||
|
Pb |
327 |
1,745 |
1,200 |
9.590534 × 103 |
8.123931 × 10-8 |
|
1,400 |
9.342134 × 103 |
6.835953 × 10-8 | |||
|
1,600 |
9.093734 × 103 |
5.823038 × 10-8 |
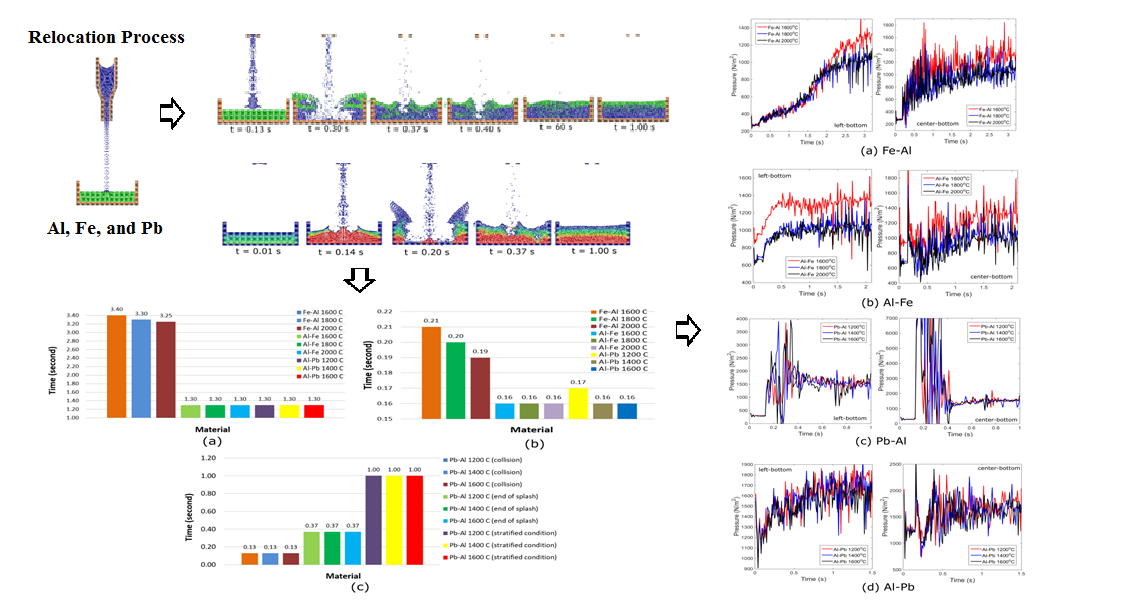
3.1. The Relocation Profiles
The
relocation process of Fe-Al can be seen in Figure 2 where all temperatures have a similar pattern, where Fe made a contact
with Al, broke through the Al layer, dived, created a layer under the Al layer,
and reached the stratified condition. When colliding with the target liquid, Fe
could break through Al as presumed that Fe has a greater density than Al. The
relocation process of Al-Fe can be seen in Figure 3 where all temperatures have a
similarity in its pattern where Al made a contact with Fe, floated above the Fe
layer, made a layer in that position, and finally reached the stratified
condition. When colliding with the target liquids, Al cannot equalize the
buoyancies of Fe. It forces Al to move on top of Fe and create a layer above
that liquid. It is because Al has a lower density than Fe. It is presumed that
the liquid with greater density needs more effort to break the layer of the
target liquid and dives under that layer. In the stratification process, the
lower density moves down gradually to form a layer under the higher density.
The higher viscous force that dominates the stratification process is expected
as the reason for this phenomenon. The collision time and the time to reach the
stratified condition for all used temperatures are similar. The collision time
was reached in 0.16 seconds and the stratified condition was reached in 1.30
seconds.
The
relocation process of Al-Fe can be seen in Figure 4. The relocation process in this
case has a similar pattern to the relocation process of Al-Fe. The time
collision and the time to reach the stratified condition are similar to those
of Al-Fe, except for the collision time at 1,400°C where Al-Pb reached it in 0.17
seconds. The relocation process of Al-Fe can be seen in Figure 5 where Pb collided with Al in
0.13 seconds and made splashes that reached up to the height of the
containment. These splashes were gone out at 0.37 seconds. After that, Pb
formed gradually a layer below Al and commenced the stratification process at
0.37 seconds. The stratified condition of Pb-Al is achieved at about a second
for all temperatures. These obtained results are similar to the cases of Pb-Al
although the temperature was different.
From those results above,
compared to Al and Fe, Pb left the bottle and reached the surface of the target
liquid in the fastest time among the used combinations. It results because,
still as the presumption, the density of Pb is the greatest among them.
Besides, the kinematic viscosity of Pb is the smallest among them. It makes Pb
flow out of the bottle container easily. However, it still needs further study
for verification. Next, the focus is targeted at the collision between liquids.
In this study, the relocation process without splashes has been found in the
cases of Fe-Al, Al-Fe, and Al-Pb. The relocation process with splashes has been
found in the Pb-Al. When Pb-Al was run, the splashes were obtained. When
switching to Al-Pb, the splashes were not obtained. It means that the splash
will arise if the fallen liquid has a higher density when the difference in
density between the two is great enough. The time duration was counted as
follows. The timing of collision started when the two liquids made direct
contact. Both liquids are considered to reach the stratified state if two
layers have formed along the length of the container. The summary of time, for
all cases, is performed in Figure 6 where at 2,000°C, to make a contact and to reach
the stratified condition, Al has the fastest time among the other temperatures.
Figure 2 Relocation process of Fe-Al
Figure 3 Relocation process of Al-Fe
Figure 4 Relocation process of Al-Pb
Figure 5
Relocation process of Pb-Al
Figure 6 The time summary for the relocation process
3.2. The Pressure Profiles
The
pressure profiles of Fe-Al can be seen in Figure 7. The higher pressure commenced
in the middle of the container and expanded to the corner of the container. In Figure 8 part (a), the pressure profiles
in two spots at the bottom of the container were investigated, i.e the
left-bottom side and the center-bottom side. The center-bottom side has higher
pressure than the left-bottom side. The results of Fe-Al at 1,600°C have higher
pressure than the other temperatures in this case. The pressure profiles of
Al-Fe can be seen in Figure 9. The patterns of these results
are similar to the pattern of Fe-Al. The higher pressure is still found in the
bottom of the container. The pressure profiles inside the container in Al-Fe
can be seen in Figure 8 part (b). The results of Al-Fe
at 1,600°C have the highest pressure among the results in this case as found in
Fe-Al.
The
pressure profiles of Pb-Al can be seen in Figure 10. In that figure, it can be seen
that the pressure profiles are similar to those of Fe-Al and Al-Fe. The bottom
side of the container has higher pressure than the wall. The pressure profiles
inside the container are displayed in Figure 8 part (c). In that figure, it can
be seen that the pressure is higher between 0.2 seconds and 0.4 seconds than
the others. It is the condition when the splash was arising. The splashes make
the pressure high. The pressure profile of Al-Pb can be seen in Figure 11. The results of this case are similar
to those of Fe-Al and Al-Fe. The pressure profiles inside the container in this
case can be seen in Figure 8 part (d). The pressures are
mostly in a disarray pattern. In regards to stratification, the difference in
density is the driving mechanism. Therefore, a higher density difference will
accelerate the stratification formation. The stratification will start from the
below area of the less dense material (Yulianto et
al., 2018; Li et al., 2013).
From
the obtained results, the relocation pattern of the liquids is similar to the
results obtained by Ilham et al. (2018) using a different liquid, where the MPS
result is compared to the experiment. Therefore, it is expected that the
temperature did not significantly impact the relocation process, which agrees
with Hidayati et al. (2020). Furthermore, the splash pattern of this
study is similar to the results of Hidayati et
al. (2021). The splash will arise if the fallen liquid
has a higher density where the difference in density between the two is big
enough. The viscosity also affects the formation of the splash. High-viscosity
fluid will show less splash formation than molten tin relocation (Li, Oka, and Furuya, 2014). 
Figure 7 The pressure profiles of Fe-Al (The pressure unit is in N/m2)
Figure 8 The pressure profiles (in N/m2) inside the container
for all configurations
Figure 9 The pressure profiles of Al-Fe (The unit of pressure is in N/m2)
Figure 10 The pressure profiles of Pb-Al (The unit of pressure is in N/m2)
Figure 11 The pressure profiles of Al-Pb (The unit of pressure is in N/m2)
Ideally, the present result should be
validated by the experiment result; however, it is very difficult to find a
study on Pb, Al, and Fe interactions. Regarding Pb-Al, there is an experiment
of melting and solidification, however, it is for crystalline size (Grabaek and Bohr, 1965). In the case of the melting behavior of
Pb-alloy with silicone oil, Masumura et al. (2015) successfully validated the experiment with
numerical simulation.
During
severe reactor accidents with several thousand degrees Celsius of temperature,
the existence of the splash may significantly affect the heat transfer process
and thus melting progression. In that regard, a study on the splash effect on
melting progression is the area to be investigated. The results give an important
understanding of how the pressure may affect the lower plenum of the reactor
when the liquids are relocated. Based on the results above, the bottom side has
higher pressure than the wall side. In a nuclear reactor, the pressure profiles
during a severe accident can provide essential information for the prediction
of the breaching and also give insight to the manufacturer of the reactor. The
present results are focused on the relocation process and its splash, in the
future, more realistic geometry and condition close to the reactor situation
during the accident is necessary to give a better understanding of the
relocation. It is also essential to compare the results with the experiment or
the other methods.
The
relocation process of some liquids has been investigated in this study. The MPS
method has been utilized to simulate the stratification process of these
liquids. This study shows that Pb-Al needs 0.13 seconds to reach collision,
Al-Fe and Al-Pb need 0.16 seconds, and Fe-Al needs more than 0.19 seconds. To
get the stratified condition, Pb-Al needs 0.63 seconds, Al-Fe and Al-Pb need
1.14 seconds, and Fe-Al needs more than three seconds. It is also found that
the difference in viscosity and density between two liquids influences the time
to reach the stratified condition — the more significant the density difference
between two liquids, the faster the stratification process. The obtained
results in this study are in a preliminary stage, which means that further
study needs to be conducted in both experiment and simulation.
AJG Ramalho, JG Marques, F. C. (1999). The Portuguese research reactors: a
tool for the next century. In International symposium on research reactor
utilization, safety and management (pp. 5–10). International Atomic Energy
Agency (IAEA): IAEA. Retrieved from http://www.iaea.org/worldatom/books
Aliffrananda,
M. H. N., Sulisetyono, A., Hermawan, Y. A., & Zubaydi, A. (2022). Numerical
analysis of floatplane porpoising instability in calm water during takeoff. International
Journal of Technology, 13(1), 190–201.
Daisuke,
M., Akifumi, Y., & Masahiro, F. (2015). Analysis of Pb-Bi Vessel Wall
Ablation Experiment with High Temperature Liquid by MPS Method. Journal of
Energy and Power Engineering, 9(11), 7401–7413.
Daisuke
Masumura, Akifumi Yamaji, & Masahiro Furuya. (2015). Analysis of Pb-Bi
Vessel Wall Ablation Experiment with High Temperature Liquid by MPS Method. Journal
of Energy and Power Engineering, 9(11), 944–954.
Duan,
G., Yamaji, A., & Sakai, M. (2022). A multiphase MPS method coupling
fluid–solid interaction/phase-change models with application to debris
remelting in reactor lower plenum. Annals of Nuclear Energy, 166,
108697.
Farrell,
K. (2012). Performance of Aluminum in Research Reactors. Comprehensive
Nuclear Materials. Elsevier Inc.
Fathonah,
N. N., Nurtono, T., Kusdianto, Madhania, S., Wahyudiono, & Winardi, S.
(2019). Numerical study of the hydrodynamic characteristics in an agitated tank
with side-entry mixer: The effect of stirrer entry angle. International
Journal of Technology, 10(3), 521–530.
Grabaek,
L., & Bohr, J. (1965). Superheating and Supercooling of Lead Precipitates
in Aluminum. Nature, 207(5003), 1238–1238.
https://doi.org/10.1038/2071238d0
Hainoun,
A., Ghazi, N., & Alhabit, F. (2019). Syria’s Benchmark Results against
Experimental Data from ETRR-2. International Atomic Energy Agency (IAEA).
Retrieved from
https://www.iaea.org/publications/13547/benchmarking-against-experimental-data-of-neutronics-and-thermohydraulic-computational-methods-and-tools-for-operation-and-safety-analysis-of-research-reactors
Hidayati,
A. N., Mustari, A. P. A., Waris, A., Yulianto, Y., & Ilham, M. (2021).
Study on Fluid Descends Vertically on Static Fluid Using Moving Particle
Semi-Implicit Method. Journal of Physics: Conference Series, 1772(1),
012007.
Hidayati,
A. N., Waris, A., Mustari, A. P. A., Apriani, N. A., Ifthacharo, M., &
Wulandari, R. (2020). The Effect of Temperature Variations on Wood’s Metal
Plate Melting Simulation by Using MPS. Journal of Physics: Conference Series,
1493(1), 012024.
IAEA.
(2008). Thermophysical Properties of Materials For Nuclear Engineering: A
Tutorial and Collection of Data. Vienna: IAEA.
Ilham,
M., YuLianto, Y., & Mustari, A. P. A. (2018). Simulation on Relocation of
Non-Compressed Fluid Flow using Moving Particle Semi-Implicit (MPS) Method. In IOP
Conference Series: Materials Science and Engineering (Vol. 407).
Kawahara,
T., & Oka, Y. (2012). Ex-vessel molten core solidification behavior by
moving particle semi-implicit method. Journal of Nuclear Science and
Technology, 49(12), 1156–1164.
Knebel,
J. U., Cheng, X., Müller, G., Schumacher, G., Konys, J., Wedemeyer, O., …
Carteciano, L. (2000). Thermalhydraulic and Material Specific Investigations
into the Realization of an Accelerator Driven System ( ADS ) to Transmute Minor
Actinides. Karlsruhe, Germany. Retrieved from
https://publikationen.bibliothek.kit.edu/270048483/3814007
Koonen,
E., Fabry, A., Chaouadi, R., Verwerft, M., Raedt, C. D. E., Winckel, S. V. A.
N., … Verwimp, A. (2000). Life Extension of the Br2 Aluminium Vessel Xa9952359.
In Research reactor utilization, safety and management Proceedings (pp.
67–68). International Atomic Energy Agency (IAEA): IAEA. Retrieved from
http://www.iaea.org/worldatom/books
Koshizuka,
S., & Oka, Y. (1996). Moving-particle semi-implicit method for
fragmentation of incompressible fluid. Nuclear Science and Engineering.
Retrieved from http://cat.inist.fr/?aModele=afficheN&cpsidt=3155698
Li, G.,
Gao, J., Wen, P., Zhao, Q., Wang, J., & Yan, J. (2020). A review on MPS
method developments and applications in nuclear engineering. Computer
Methods in Applied Mechanics and Engineering, 367, 113166.
Li, G.,
Oka, Y., & Furuya, M. (2014). Experimental and numerical study of stratification
and solidification/melting behaviors. Nuclear Engineering and Design, 272,
109–117.
Li, G.,
Oka, Y., Furuya, M., & Kondo, M. (2013). Experiments and MPS analysis of
stratification behavior of two immiscible fluids. Nuclear Engineering and
Design, 265, 210–221.
Machut,
M., Sridharan, K., Li, N., Ukai, S., & Allen, T. (2007). Time dependence of
corrosion in steels for use in lead-alloy cooled reactors. Journal of
Nuclear Materials, 371(1–3), 134–144.
Mustari,
A. P. A., & Oka, Y. (2014). Molten uranium eutectic interaction on
iron-alloy by MPS method. Nuclear Engineering and Design, 278,
387–394.
Mustari,
A. P. A., Oka, Y., Furuya, M., Takeo, W., & Chen, R. (2015). 3D simulation
of eutectic interaction of Pb-Sn system using Moving Particle Semi-implicit
(MPS) method. Annals of Nuclear Energy, 81, 26–33.
Mustari,
A. P. A., & Takahashi, M. (2011). Study on corrosion of welded steel for
LBE-cooled fast reactors. Progress in Nuclear Energy, 53(7),
1073–1077.
N.
Chandran, J. Gunasekaran, D. Nithyanand, & C. Vinoth Kumar. (2018). Flow
Analysis of Molten Metal through various Ingates using water models. International
Journal of Engineering Research and Technology, 06(02), 5–7.
Rivai,
A. K., & Takahashi, M. (2010). Corrosion investigations of Al-Fe-coated
steels, high Cr steels, refractory metals and ceramics in lead alloys at 700
°C. Journal of Nuclear Materials, 398(1–3), 146–152.
Saha,
S. K., & Nandi, N. (2017). Numerical study about the change in flow
separation and velocity distribution in a 90o pipe bend with/without
guide vane conditions. International Journal of Technology, 4,
681–689.
Su’ud,
Z., Irka, F. H., Imam, T. T., Sekimoto, H., & Sidik, P. (2013). Desain
study of Pb-Bi cooled fast reactors with natural uranium as fuel cycle input
using special shuffling strategy in radial direction. Advanced Materials
Research, 772, 530–535.
Talaat,
K., Lee, S., Lee, Y., Anderoglu, O., Cakez, C., Ghosh, S., … Ferroni, P.
(2019). Numerical investigation of molten lead flow in a closed loop to
estimate pressure demand. Transactions of the American Nuclear Society, 121,
1787–1790.
Utama,
I. K. A. P., Aryawan, W. D., Nasirudin, A., Sutiyo, & Yanuar. (2021).
Numerical Investigation into the Pressure and Flow Velocity Distributions of a Slender-Body
Catamaran Due to Viscous Interference Effects. International Journal of
Technology, 12(1), 149–162.
Widiawati,
N., Su’ud, Z., Irwanto, D., & Sekimoto, H. (2018). Neutronic Comparison
Study between Pb(208)-Bi and Pb(208) as a Coolant in the Fast Reactor with
Modified CANDLE Burn up Scheme. Journal of Physics: Conference Series, 1090,
012071.
Yulianto,
Y., Hidayati, A. N., Mustari, A. P. A., Ilham, M., & Pramuditya, S. (2018).
Moving Particle Semi-implicit (MPS) Utilization in Analyzing the Stratification
Behavior of Immiscible Liquid. IOP Conference Series: Materials Science and
Engineering, 407, 012189.
Yulianto,
Y., Mustari, A. P., Ilham, M., Hidayati, A. N., & Hatmanti, S. (2019).
Moving Particle Semi-implicit Method in Simulating Water-Oil Penetration. Indonesian
Journal of Physics, 30(2), 24–33.