Design Exploration and Optimization of a Multi-Corner Crash Box under Axial Loading via Gaussian Process Regression
Corresponding email: annisa.jusuf@itb.ac.id
Published at : 24 Dec 2024
Volume : IJtech
Vol 15, No 6 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i6.7278
Jusuf, A., Jarwadi, M.H., Hastungkorojati, D.G., Gunawan, L., Akbar, M., Zakaria, K., Izzaturrahman, M.F., Palar, P.S., 2024. Design Exploration and Optimization of a Multi-Corner Crash Box under Axial Loading via Gaussian Process Regression. International Journal of Technology. Volume 15(6), pp. 1749-1770
| Annisa Jusuf | Mechanics of Solids and Lightweight Structures Research Group, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Maulana Hayu Jarwadi | Master Program of Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Dhimaz Galang Hastungkorojati | Master Program of Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Leonardo Gunawan | Dynamics and Control Research Group, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Mahesa Akbar | College of Business, Technology, and Engineering, Sheffield Hallam University, Sheffield S1 1WB, United Kingdom |
| Kemas Zakaria | Master Program of Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Muhammad Faiz Izzaturrahman | Master Program of Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
| Pramudita Satria Palar | Fluid Dynamics and Propulsion Research Group, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Bandung 40132, Indonesia |
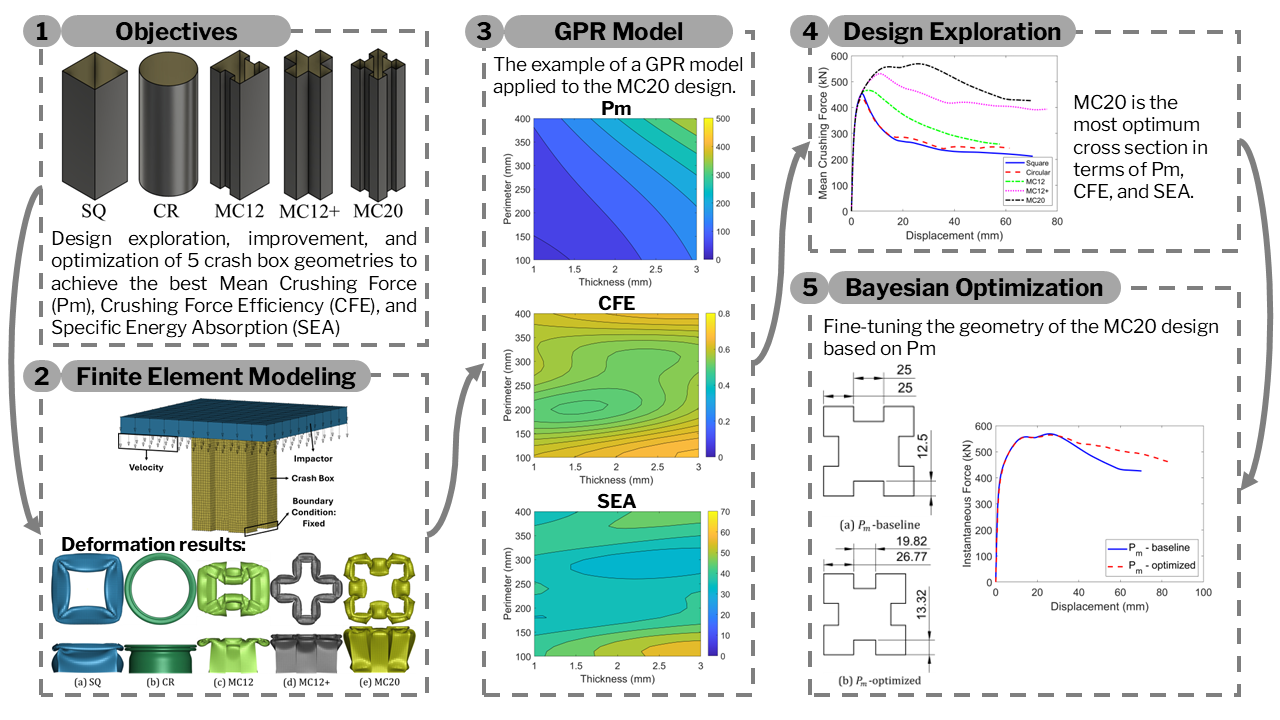
Crash box is the most commonly used energy-absorbing systems for increasing transportation safety. Based on this system, design optimization of crash box is important to meeting safety standards with high performance. Therefore, this study aimed to propose a crucial crash box design featuring a 20-corner structure. This new design was expected to increase the number of folds and reduce the size upon impact, which can further elevate specific energy absorption (SEA). In addition, the study implemented a Gaussian Process Regression (GPR) surrogate model for the first time to optimize the multi-corner crash box design. This method reduced the computational cost of the design optimization process while effectively handling complex configurations. The optimization also focused on dimensional parameters such as thickness and perimeter. An explicit nonlinear finite element method was used for axial loading analysis to assess the crash impact performance. The computational results showed good agreement with experimental data where the performance of the 20-corner structure design was compared with other shapes including square, circular, and 12-corner designs. The results showed that the 20-corner structure design provided the most optimum SEA and Crushing Force Efficiency (CFE). Furthermore, the optimized 20-corner design via GPR-model led to a further performance increment with an increase of 8-9% higher SEA and CFE. The following main conclusions can be drawn (i) the cross-sectional geometry significantly influenced crashworthiness performance with the MC20 configuration achieving the best Pm, CFE, and SEA values compared to other configurations. Therefore, the study concluded that the MC20 configuration was the most efficient among the other configurations; (ii) GPR proved advantageous in the optimization process, offering flexibility for complex nonlinear functions, reducing computational costs, and providing error predictions to further refine the optimization model; and (iii) optimization of the MC20 configuration using the GPR surrogate model focused on a single objective which was to maximizing Pm.
Crashworthiness; Crash box; Design optimization; Gaussian process regression; Multi corner
Crashworthiness is a critical criterion that should be considered in designing a vehicle (Skhvediani et al., 2023), as it requires vehicle structures to absorb kinetic energy and minimize passengers’ injury during an impact collision. Crash box plays a central role in crashworthiness and is positioned between the bumper and side rails in land vehicles. The shape, configuration, and size of a crash box are key determinants of the performance. Basic shapes such as rectangular and circular designs have been extensively used while studies on more complex shapes including multi-corner designs have significantly increased over the last two decades to further enhance crashworthiness. This study introduces a crucial multi-corner crash box design aimed at improving energy absorption and crushing force capabilities. An advanced optimization technique is also applied to streamline the design process and enhance crash box performance.
Crash box is often designed as thin-walled columns due to the high energy absorption, ease of manufacturing, and lightweight structure (Olabi, Morish, hashmi, 2007). The crashworthiness of thin-walled columns depends on factors such as material properties, cross-section shape, configuration, wall thickness, and cross-section perimeter (Wu et al., 2017). Among vehicle collisions, frontal impacts typically cause the most severe injuries and fatalities (Bastien, 2014), which has spurred examination into innovative cross-section designs for crash boxes, as evidenced by numerous studies over recent decades (Christensen, 2022).
Several previous crashworthiness studies focus on metal columns such as steel (Xu et al., 2014; Abedrabbo et al., 2009) and aluminum (Shahi and Marzbanrad, 2012; Galib and Limam, 2004). Recently, studies have expanded to explore columns made from alternative materials, such as composites (Mamalis et al., 2004; Hull, 1991) and hybrid (Wang et al., 2020; Reuter and Tröster, 2017). However, cross-sectional shape and configuration remain important in influencing crashworthiness. Various cross-section shapes have been examined, including square (Lu et al., 2017; Zhang et al., 2014), hexagonal (Alkbir et al., 2014; Hou et al., 2007), octagonal (Liu and Day, 2007), circular (Kumar and Maneiah, 2019; Liu, Huang, and Qin, 2017; Abramowicz and Jones, 1986), top-hat (Dimas et al., 2014; Tarigopula et al., 2006; Schneider and Jones, 2003; White and Jones, 1999), and double-hat shapes (White and Jones, 1999). In addition to these standard cross-sections, unique column shapes such as multi-cell (Lu, Deng, and Liu, 2023; Nagarjun et al., 2020; Zhang et al., 2019; Kumar et al., 2019; Jusuf et al., 2011; Yamashita, Gotoh, Sawairi, 2003; Abramowicz and Wierzbicki, 1989), multi-corner or polygonal (Zhang and Huh, 2010; Zhang and Zhang, 2012; Godat, Legeron, and Bazonga, 2012; Tang, Liu, and Zang, 2012; Liu, et al., 2015; Abbasi et al., 2015; Reddy, Abbasi, and Fard, 2015), and origami-inspired designs (Yuan et al., 2019; Zhou, Zhou, and Wang, 2017) have been developed.
Studies show that increasing the column’s thickness can improve the crash box’s energy absorption capacity (Qi, Yang, Dong, 2012; Liu, 2008). Alternatively, energy absorption can also be improved through multi-corner column designs, as several studies have shown (Liu et al., 2015; Abbasi et al., 2015; Reddy, Abbasi, and Fard, 2015; Zhang and Zhang, 2012; Godat, Legeron, and Bazonga, 2012; Tang, Liu, and Zang, 2012; Zhang and Huh, 2010). Crashworthiness analysis has been conducted on multi-corner cross-sections, such as rectangular, hexagonal, octagonal, and 12-edge profiles (Abbasi et al., 2015) (Reddy, Abbasi, and Fard, 2015). Results show that columns with a 12-edge profile have higher SEA and CFE than others, suggesting that increasing the number of corners improves energy absorption efficiency. Recently, (Zhang et al., 2022) conducted a numerical analysis of energy absorption in 12-corner columns with variable thicknesses and estimated mean crushing force using a theoretical approach derived from plastic deformation theory for thin-walled columns. Results suggest that plastic collapse models for prismatic columns can be applied to multi-corner designs.
Over the last decade, optimization techniques, such as genetic algorithms and artificial neural networks, have become effective tools for enhancing crash box performance. Insights from these optimization studies are crucial for understanding crashworthiness and guiding future design improvements. Various authors have conducted crash box optimizations (Borse, Gulakala, and Stuoffel, 2024; Djamaluddin, 2024; Jongpradist, et al., 2024; Bhutda, Sonje, and Goel, 2023; Wang, et al., 2022; Ciampaglia, et al., 2021; Wang, et al., 2020; Chen, et al., 2019; Pirmohammad and Esmaeili-Marzdashti, 2019; Fang, et al., 2017).
Wu et al. (2017) introduced a discrete optimization algorithm using orthogonal arrays to optimize Specific Energy Absorption (SEA) in Fourier-section tubes. Chen et al. (2019) used multi-objective optimization with surrogate models to identify the optimal design for hybrid multi-cell columns, combining circular and square sections in various configurations. Fang et al. (2017) reviewed essential studies and recent developments in structural crashworthiness and energy absorption optimization. Additionally, Pirmohammad and Esmaeili-Marzdashti (2019) optimized hole shapes and sizes in square and octagon thin-walled structures using genetic algorithms (NSGA-II) and artificial neural networks to achieve optimal configurations.
Wang et al. (2020) introduced a bionic multi-corner crash box inspired by the structure of the cactus. This multi-objective optimization design is developed using the response surface model (RSM) and Latin hypercube design. Wang et al. (2020) showed that the bionic crash box reduced the vehicle damage, increases energy absorption, and creates a stable folding deformation. Wang et al. (2022) explored a new hexahedral pyramid crash box, using the RSM and a multi-objective evolutionary algorithm with a detection and escape strategy (MOEA/D-DAE) to improve crash box performance. Results demonstrated that the hexahedral pyramid crash box has superior energy absorption compared to hollow, hexagonal honeycomb, and re-entrant crash boxes. Moreover, the optimized hexahedral pyramid design offers enhanced energy absorption and more stable folding deformation. Recent studies have also examined optimization approaches for advanced designs with complex configurations and innovative materials, such as origami-shaped crash boxes (Ciampaglia et al., 2021), foam-filled designs (Djamaluddin, 2024) and boxes made from functionally graded materials (Jongpradist et al., 2024).
Beyond traditional methods, machine learning has evolved as a valuable approach in design optimization. Gaussian Process Regression (GPR), also known as Kriging surrogate modeling, has gained popularity in engineering for its ability to reduce computational costs while delivering accurate solutions in less time (Palar and Shimoyama, 2019). This model can not only predict outcomes but also provide error estimates, improving Bayesian optimization and further supplying supplementary information in a relatively straightforward manner. GPR’s flexibility makes the model ideal for capturing complex, nonlinear responses (Palar, Zuhal, and Shimoyama, 2020).
Previous study outlines the importance of geometric and dimensional factors in enhancing energy absorption for crashworthiness, material deformation, and failure characteristics. Therefore, exploring and optimizing crash boxes with varied cross-sections and dimensions is necessary to understand how these factors impact overall performance. Despite the potential of multi-corner crash boxes, a comprehensive comparison across different cross-sectional shapes remains unexplored. Studies show that increasing the number of corners enhances energy absorption and SEA. Multi-corner crash boxes have been implemented in practical applications, as seen in designs by Ford (Cheng, 2011) and Sumitomo (Nakazawa et al., 2005). This study proposes a new 20-corner multi-corner design, previously unexplored, with shape optimization.
The proposed design features recessed sections on all four sides to increase the number of folds and reduce their size upon impact, enhancing SEA values. For future applications, crash boxes could be produced using 3D printing to incorporate complex geometries such as auxetic and lattice structures (Kholil et al., 2023; Hou et al., 2023; Seek et al., 2022).
Basic shapes such as square and circular, are commonly used in crash boxes for ease of manufacture. In this study, a 20-corner design derived from a square cross-section is proposed to maintain manufacturing simplicity. Additionally, other multi-corner shapes, such as a 12-corner H-like and a 12-corner plus sign-like design, are evaluated for comparison. Parametric studies are conducted on shape dimensions, including perimeter and thickness. The crashworthiness parameters—mean crushing force (Pm), SEA, and Crushing Force Efficiency (CFE)—are analyzed using finite element methods.
The GPR model based on Rasmussen (2003) is implemented to conduct optimization on the design of the 20-corner shape. A fine-tuning of the most efficient cross-section in terms of crashworthiness performance is performed using a Bayesian optimization procedure based on Jones’s research (Jones, Schonlau, and Welch, 1998). The GPR-based optimization is particularly effective in approximating nonlinear responses, which are characteristic of the challenges addressed in this study. Additionally, GPR provides point-wise predictive uncertainty, an essential feature for Bayesian optimization, which is not available in models such as artificial neural networks or polynomial regression. This optimization process aims to deliver a high-performance 20-corner configuration based on Pm, offering greater resistance to vehicle structure during frontal impacts while keeping general dimensions within practical limits.
2.1. Crashworthiness characteristics
This study examined three main crashworthiness parameters, namely (1) Mean Crushing Force (Pm), (2) Specific Energy Absorption (SEA), and (3) Crushing Force Efficiency (CFE).
2.1.1. Mean Crushing Force
Mean crushing force (Pm) represented the total energy absorption (EA) divided by the total crushing length ( max), as shown in Equation 1.
Where P denoted the
crushing force and represented the
crushing length (displacement) along the axial direction of the crash box
structure. A higher Pm
2.1.2. Specific Energy Absorption
2.1.3. Crushing
Force Efficiency
Crushing force efficiency (CFE)
was the ratio of the Pm
Where Pmax referred to the maximum force which was kept low to reduce the load transmission from the crash box to the vehicle’s main body. A high CFE implied that the design absorbed energy effectively by maximizing energy absorption while minimizing peak force. In this study, impact behavior of crash box structures was analyzed for Pm, CFE, and SEA by varying the cross-sectional shapes, thickness, and perimeter.
2.2. GPR Surrogate Model
A surrogate model captured the relationship between the input and output variables, fx, through an estimated function fx, where x=x1,x2,…,xmT with m being the design variables. The initial step included preparing the design of experiments X=x1,x2,…,xnT and the corresponding responses y=y1,y2,…,ynT=fx1, fx2,…, fxnT where n was the sample size. GPR assumed that the prediction fx was the mean of realizations of Gaussian processes represented by the following Equation 4.
Where µx represented the mean term and Zx denoted the stochastic process. GPR assumed correlations between different points defined by the correlation function kxi,xj, as shown in Equation 5.
The implementation in this study used the squared-exponential correlation function as shown in Equation 6.
Where was the lengthscale of the correlation function. In GPR, a k-dimensional correlation function was constructed as a product of one-dimensional components. Thus, lengthscales required tuning, forming a vector =1,2,…,m.
To capture correlations among all samples in the design, the matrix (of size n×n) was constructed, where each component. The i, j-th component of the matrix equals to coryi,yj=kxi,xj. The stochastic term of GPR, Zx, was formulated as follows
Where represented the n×1 correlation vector between an arbitrary point x* with the experimental design . The prediction structure of GPR then reads as
Beside the prediction, GPR also directly provided the uncertainty estimate, as given by
Where denoted the GPR variance. The implementation of GPR considered numerical noise by adding a regression factor to the correlation matrix. Therefore, the correlation matrix became
where I represented the identity matrix.
The optimum hyperparameters were aimed by minimizing the negative of ln-likelihood function, as shown in Equation 10.
The GPR mean was estimated by the maximum possible estimation. To accomplish the hyperparameter optimization, this study used the combination of genetic algorithm and hill-climbing to increase the chance of finding the global optimum.
Bayesian optimization enriched the experimental data by evaluating a solution that maximized the acquisition function (Jones, Schonlau, and Welch, 1998). The Bayesian optimization was initiated by seeding the design space with initial samples. The formulation of the expected improvement as the acquisition function, given an established GPR prediction at an arbitrary point x as shown in Equation 11.
Where ymin represented the best solution observed (in the context of minimization).
At every iteration of Bayesian optimization, the sample point with the highest (i.e., xopt) was found by a genetic algorithm followed by a local search. The xopt was then evaluated by a computer simulation and added to the experimental design. The process was then repeated until the computational budget was exhausted.
Numerical Simulation and Optimization Procedures
3.1. Geometrical Detail
In this study, five cross-section configurations were studied, including basic geometries (square 'SQ' and circular 'CR' crash boxes) and more complex, multi-corner geometries, such as 12-corner structures with H-like shapes ('MC12'), 12-corner structures with a positive sign-like shape ('MC12+'), and 20-corner crash boxes ('MC20'), as shown in Figure 1.
Figure 1 Depictions of various cross-section used in the design exploration phase
The inclusion of basic geometries allowed an observation of the performance gains achieved by the multi-corner designs. Two different square crash boxes were analyzed where the first was labeled as 'SQV' which served to validate the finite element model, and the second called 'SQ' for parametric studies.
Table 1 shows the details of the crash boxes in the study. The first square crash box (SQV) followed experimental studies previously conducted by Jusuf et al. (2011; 2015) and Gunawan (2013). The second square crash box (SQ) was among the five models created with the same mass and length (150 mm), while thickness and perimeter were set as variable design factors. The thickness ranged from 1 to 3 mm, and the perimeter spanned from 120 to 400 mm. The lengths of each side for all cross-sections were adjusted so that the resulting perimeter matched the specified design values.
Table 1 Nomenclature of crash Box
For fair comparison, side lengths of each cross-section were proportionately adjusted to yield a perimeter equal to the given design values. In MC12, MC12+, and MC20, relationships between side lengths were fixed. For MC12, when the longest side length was defined as amc12, the other sides were set to amc12/3 and amc12/6 (see Figure 2). In MC20, when the longest distance between points on the edge was amc20, the other sides were amc20/3 and amc12/20 (refer to Figure 2).
Figure 2 Relationship between side lengths for the MC12 and MC20 crash box used in the design exploration phase
For design exploration, the thickness bounds were set from 1 to 3 mm, and the perimeter bounds from 120 to 400 mm. Thirty-one sampling points were generated using Halton (1964) sampling method. This was joined with an additional four sampling points placed at the corners of the design space.
3.2. Mechanical Properties
The crash box material used was mild steel (St37) with a Young's modulus of 222 GPa, a Poisson's ratio of 0.3, a density of 7.33×106 kg/mm³, a yield strength of 0.29 GPa, and power-law hardening of 0.157. Figure 3 illustrates the true stress-plastic strain curve where the material properties were defined as elastoplastic, accounting for strain rate effects. Due to the material’s strain rate sensitivity, Cowper-Symonds parameters D and q were applied, valued at 6844 s-1 and 4.12, respectively (Jusuf et al., 2015). Properties for the impactor material included a Poisson ratio of 0.3 and a density of 7.5×10-4 kg/mm3.
Figure 3 True Stress-Effective Plastic Strain of Mild Steel St37
3.3. Finite Element Modelling and Validation
3.3.1. Finite Element Modelling
The crash box performance analyses were conducted using explicit nonlinear dynamic analysis software. The typical finite element model for crushing analysis of a crash box was depicted in Figure 4. A crash box was modelled as a thin-walled column subjected to the axial impact loading through the impactor. The impactor mass was 30 kg, modelled as a rigid body to avoid energy absorption on the impactor. The impactor could translate freely in the axial direction while constrained in other directions, with a velocity of 10 m/s in the negative y-direction as shown in Figure 4. The lower end of the column was made as a fixed constraint which implied that there was no translation and rotation in any direction, as depicted in Figure 4. The column material was modelled using a piecewise linear plasticity because the column was expected to absorb energy by the plasticity mechanism.
Figure 4 The typical crash box model in the finite element simulation
Figure 5 Result of mesh convergence study
The column walls were modelled using quad-node shell elements. To specify the element size, a convergence test was performed by varying the size of the mesh elements in a square column with a perimeter of 200 mm and a thickness of 1 mm. The result showed that the scheme with a single mesh element of 3×3 mm2 was adequate to ensure reasonable accuracy, as shown in convergence test outcome in Figure 5. Two contact algorithms were used namely ’automatic nodes to surface’ and ’automatic single surface.’ The ‘automatic nodes to surface’ defined the contact between the impactor and the crash box. On the other hand, the ‘automatic single surface’ contact was applied to avoid self-penetration on the column wall during folding creation. The static and dynamic friction coefficients for all contact mechanisms were 0.4 and 0.3 (Zhang et al., 2019) respectively.
3.3.2. Validation
Validation of the finite element model was conducted using the SQV cross-section, as examined by Jusuf et al. (2011; 2015) and Gunawan (2013) to ensure accuracy in the modeling approach. Upon successful validation, the model was employed to analyze and optimize the crash box structures for the study. Table 2 and Figure 6 show a comparison of the crashworthiness characteristics of the validated crash box structure.
Table 2 SQV crashworthiness characteristic comparison
*(Jusuf, et al., 2015); **(Gunawan, 2013); ***Present study
(a)
(b)
Figure 6 (a) Crushing force response of SQV mild steel square columns, (b) Deformation modes of square columns (i) numerical (Jusuf et al., 2015), (ii) experimental (Gunawan, 2013), (iii) numerical validation
3.4. Design Exploration and Optimization Framework
Before examining the design exploration and optimization results in detail, several preparatory steps were necessary to ensure that the simulated samples could be optimized using the GPR surrogate model. As explained in Section 3.1, there were variations in thickness and perimeter
values across five cross-sectional configurations, which were detailed in Table 1. A finite element crash box simulation was then performed for each variation in thickness and perimeter for all configurations. From this simulation process, an instantaneous force graph was obtained and processed to determine the crash box performance parameters namely Pm, CFE, and SEA, which could be calculated using the equation in Section 2.1. The influence of perimeter and thickness on the three crashworthiness characteristics was further analyzed based on these results. In particular, the most efficient cross-section in terms of the mentioned metrics was determined from this procedure. Additionally, the trade-off between the three-performance metrics was also made visible with the help of GPR. The instantaneous and mean crushing forces of the solutions of interest were also analyzed to identify important design insights.
After completing the design exploration, Bayesian optimization was applied to identify the most efficient cross-sectional configuration. Using the MC20 configuration results as input, the GPR model was employed to perform the optimization process to determine when further improvements were possible. The Kriging-based optimization algorithm then fine-tuned the crash box geometry by fixing perimeter and thickness values to their optimal levels. This process identified an optimal geometry by refining these geometric details, with the initial perimeter and thickness values of the cross-section having the highest Pm serving as the baseline design. The primary aim was to maximize the crash box’s potential in terms of mean crushing force (Pm) Pm. Finally, the optimal Pm value from this optimization was compared with simulation results for the optimal configuration, allowing for an assessment of performance improvement after fine-tuning.
4.1. Design exploration result
The analysis began with design exploration results to evaluate how cross-sectional shapes influenced crash box performance, as outlined in Table 1. The GPR plots for Pm, CFE, and SEA, illustrated through surface and contour plots in Figures 7, 10, and 11, respectively, show trends between thickness and perimeter values and crashworthiness characteristics for each configuration. These trends were derived using Gaussian regression based on the simulation results of 35 samples, each with consistent variation distributions for different configurations. The contours and color gradients in the GPR plots indicate how crashworthiness metrics varied with changes in perimeter and thickness, providing a clear view of these factors’ effects. From the GPR plots, the minimum and maximum values of Pm, CFE, and SEA for each cross-section were summarized in Table 3.
4.1.1. Comparison based on
Figure
7 showed that the cross-sectional shape significantly affected the structural
impact behaviour with each cross-section generating unique values.
Figure 7 GPR plots for the Pm of the five cross-sectional shapes
The
first clear trend observed was that increasing thickness and perimeter
generally led to higher mean crushing forces across all cross-section types.
The second trend showed that, for all configurations, the optimal Pm value was achieved at a pattern consistent across crash box types (as depicted in Figures 7(a) to 7(e)).
Figure
8 presented the instantaneous crushing force versus crushing length and the
mean crushing force versus crushing length for all cross-sections with the
maximum Pm In Figure 8(a), differences in instantaneous force trends
showed variations in each configuration's ability to withstand impact forces,
which consequently influenced mean crushing force values displayed in Figure 8(b).
Comparing configurations with the same perimeter and thickness, it was evident
that certain cross-sectional shapes performed better. At maximum perimeter and
thickness, the MC12, MC12+, and MC20 configurations suggested higher mean
crushing forces than the SQ and CR shapes, with MC20 achieving the highest Pm and SQ the lowest. This trend further
suggested that increasing the number of corners improves performance in terms
of mean crushing force.
Figure 8 Instantaneous and Mean Crushing
Force for the Maximum Pm Configurations
The mean crushing force was found to be more
sensitive to changes in thickness than perimeter. Interestingly, the circular
(CR) shape, which theoretically represents a crash box with infinite corners,
did not perform as well as the multi-corner shapes in terms of mean crushing
force (Pm).
Even with the same number of corners, MC12+ outperformed MC12 and further
outlined that geometry played a crucial role in performance. Progressive
buckling occurred across all shapes during deformation with SQ, CR, and MC12
forming longer wavelength folds. On the other hand, MC12+ and MC20 developed
shorter wavelength folds which enabled the elements to absorb more energy. The
deformation patterns of each crash box shape revealed significant differences
in crashworthiness performance, as shown in Figure 9.
The SQ shape
exhibited progressive buckling, while the CR shape displayed smooth, uniform
deformation. In contrast, the multi-cell configurations (MC12, MC12+, and MC20)
showed complex folding and buckling, enhancing load distribution and energy
absorption. These findings suggested that a crash box’s performance depends not
only on corner count but also on the geometry of the multi-corner section.
Specifically, increasing thickness, perimeter, and the number of corners led to
shorter fold wavelengths, contributing to a higher
Figure 9 Deformed shapes at maximum
Figure 10 GPR Plots for the CFE
of the five cross-sectional shapes
4.1.2. Comparison based on CFE
Figure
10 presented the GPR plots for CFE across all crash box configurations,
similar to Figure 7, which showed the impact of variations in thickness and
perimeter on crashworthiness characteristics. For simple shapes (SQ, CR, MC12),
results showed that increasing thickness while reducing perimeter improved CFE,
as shown in Figures 10(a) through 10(c). Significantly, a trade-off evolved
between CFE and mean crushing force Pm.
This trade-off implied maximizing CFE would lead to reduced performance
in terms of Pm and
Although simple
shapes such as SQ, CR, and MC12 showed a steady increase in CFE with
greater thickness and smaller perimeter, the trend was more complex for MC12+
and MC20. This complexity implied that configuring perimeter and thickness for
MC12+ and MC20 required caution, as the relationship with CFE did not
follow a simple trend, especially for MC20. Results also showed that although
CR achieved the highest possible CFE among the cross-sections, this
advantage was minimal compared to the others. Furthermore, Figure 10 suggested
a contrasting CFE trend for MC12+ and MC20 compared to the simpler
shapes. Simple shapes saw increased CFE with higher thickness and lower
perimeter, while MC12+ and MC20 displayed two local maximum values, nearly
equal in peak, as indicated in Figures 10(d) and 10(e). Furthermore, Table 3
showed that MC20's CFE slightly outperformed MC12+.
4.1.3. Comparison Based on SEA
As shown in Figure 11,
high SEA was achieved by reducing perimeter and increasing thickness in
simpler shapes (SQ, CR, MC12). This trend mirrored the one for CFE,
where maximizing thickness and minimizing perimeter led to higher CFE
values. Among the shapes, SQ had the lowest SEA, while CR and MC12
displayed higher SEA levels, respectively. For MC12+ and MC20, the SEA
trend proved more complex, featuring two local maximum values nearly equal in
peak, as depicted in Figures 11(d) and 11(e).
Figure 11 GPR plots for the SEA of the
five cross-sectional shapes
Comparison all five
shapes, SQ had the lowest SEA while MC20 achieved the highest SEA.
This outcome showed that given the same energy absorption, each configuration's
deformed mass varied, resulting in differing SEA values. The SEA
criterion is critical in crash box structures to minimize collision-induced
damage. In such structures, corners act as primary energy absorption points,
making designs with more corners preferable, as these increased SEA
values by reducing deformed mass. Therefore, the crash box's cross-sectional
shape substantially affected energy absorption effectiveness. Even with an
identical number of corners, the precise shape needed careful design, as shown
by the differing performances of MC12 and MC12+.
4.1.4. Comparison Based on
Table 3 summarized the optimal designs across various crashworthiness performance metrics (Pm, CFE, and SEA) for each cross-section. Analysis of the surface and contour plots for Pm, CFE, and SEA, as depicted in Figures 7, 10, and 11, respectively, indicated a clear conflict among the three parameters. The MC20 configuration achieved the highest values for Pm, CFE, and SEA. Although simpler cross-sections such as SQ and CR were easier to manufacture, the sections proved less efficient at impact energy absorption than MC12+ and MC20. A clear trade-off existed between manufacturability and crashworthiness in crash box design. However, selecting the exact geometry for multi-corner crash box designs required careful consideration.
Table 3 Optimized values of Pm, CFE, and SEA, and the
corresponding configuration for all cross-sections
4.2. Bayesian optimization of the maximum Pm 20-corners crash box
Based on the results
from Section 4.1, the GPR-based design exploration identified MC20 as the most
efficient geometry in terms of Pm,
CFE, and SEA, surpassing other shapes in several design aspects.
The design exploration maintained a fixed cross-sectional shape, optimizing
only thickness and perimeter. Consequently, further performance improvements
for the MC20 crash box remained feasible through additional optimization. Bayesian
optimization was subsequently performed to enhance MC20's performance by
keeping the optimized thickness and perimeter values fixed and adjusting the length of each wall segment, as shown in Figure 12(a).
Figure 12 Design variables and design space
for the fine-tuning of the MC20 geometry using Bayesian optimization with
maximum
Figure
12(a) showed the design variables used to fine-tune the MC20 shape, represented
by dimensions a, b, and c. These lengths referred to the
mid-plane of the walls, with the crash box symmetrical along the x- and y-axes.
The total length of all sides was required to equal 400 mm, establishing a
relationship among the three variables. Dimensions a and b were selected as
design variables, while c remained dependent which yielded the equation:
|
|
As discussed in
Sections 4.1, the thickness and the perimeter of optimized MC20 were For this configuration, the corresponding variables
for the baseline design were a = 25 mm and b = 12.5 mm,
represented by blue square shape in Figure 13. The optimization began with ten
random samples, indicated by black circles. Most initial samples appeared in
blue contours, suggesting room for further improvement. Adding ten more samples
in the orange to red areas marked an enhancement in the crash box dimensions,
increasing the Pm value. This process identified the optimal
sample with the highest
Figure 13 The surface and contour plot for the optimization of the MC20 design to maximize Pm. Baseline (blue square shape), Samples (black circle shape), Optimum (green diamond shape)
The
geometries of the baseline and optimized designs as shown in Figure 14
suggested longer sides a and b in the optimized version,
contributing to improvements across all criteria. As depicted in Figure 15, the
optimized design exhibited better energy absorption than the baseline,
benefiting from a progressive buckling mode essential for crashworthiness.
These results underscored Bayesian optimization's ability to refine the MC20
design further, with side length adjustments significantly enhancing the
20-corner configuration's performance.
Figure 14 The Pm 20-corner design (baseline and optimized). The dimensions are in millimeters
Figure 15 Instantaneous and cumulative mean
crushing force for the Pm-baseline
and the
Table 4 Performance comparison between the Pm-baseline and the Pm-optimized 20-corner design. The two designs experienced progressive buckling
|
Model |
|
|
|
|
|
|
|
Baseline |
25.00 |
12.50 |
25.00 |
425 |
0.68 |
46.99 |
|
Optimized |
26.77 |
13.32 |
19.82 |
460 |
0.74 |
51.04 |
In
conclusion, the design exploration and optimization of crash box with various
cross-sections which focused on multi-corner designs were successfully
conducted. This exploration varied the thickness and perimeter across five
cross-sectional shapes namely square (SQ), circular (CR), 12-corner H-like
shape (MC12), 12-corner plus-sign shape (MC12+), and 20-corner (MC20). The GPR
surrogate model was applied to construct response surfaces for Pm
Annisa
Jusuf and Pramudita Satria Palar were funded in part through the Penelitian,
Pengabdian kepada Masyarakat dan Inovasi
ITB scheme (P2MI 2024) administered by Institut Teknologi Bandung, Indonesia.
Abbasi, M., Reddy, S., Ghafari-Nazari, A., Fard, M.,
2015. Multiobjective Crashworthiness Optimization of Multi-Cornered Thin-Walled
Sheet Metal Members. Thin-walled Structures, Volume 89, pp. 31–41. https://doi.org/10.1016/j.tws.2014.12.009
Abedrabbo, N., Mayer, R., Thompson, A., Salisbury, C.,
Worswick, M., Riemsdjik, I., 2009. Crash Response of Advanced High-Strength
Steel Tubes: Experiment and Model. International Journal of Impact
Engineering, Volume 36(8), pp. 1044–1057. https://doi.org/10.1016/j.ijimpeng.2009.02.006
Abramowicz, W., Jones, N., 1986. Dynamic Progressive
Buckling of Circular and Square Tubes. International Journal of Impact
Engineering, Volume 4(4), pp. 243–270. https://doi.org/10.1016/0734-743X(86)90017-5
Abramowicz, W., Wierzbicki, T., 1989. Axial Crushing
of Multicorner Sheet Metal Columns. Applied Mechanics, Volume 56(1), pp.
113–120. https://doi.org/10.1115/1.3176030
Alkbir, M., Sapuan, S., Nuraini, A., Ishak, M., 2014. Effect of Geometry on
Crashworthiness Parameters of Natural Kenaf Fibre Reinforced Composite
Hexagonal Tubes. Material and Design, Volume 60, pp. 85–93. https://doi.org/10.1016/j.matdes.2014.02.031
Bastien, C.,
2014. The Prediction of Kinematics and Injury Criteria of Unbelted Occupants
Under Autonomous Emergency Braking, Coventry University
Bhutda, S., Sonje, S., Goel, M.D., 2023.
Multi-Objective Optimization of Foam-Filled Tubes to Enhance the
Crashworthiness Characteristics Under Impact Loading. Journal of the
Brazilian Society of Mechanical Sciences and Engineering, Volume 45(9), p.
483. https://doi.org/10.1007/s40430-023-04398-1.
Borse, A., Gulakala, R., Stoffel, M., 2024.
Multi-Parameter Design Optimization of Crash Box for Crashworthiness Analysis. Proceedings
in Applied Mathematics and Mechanics, p. e202400096. https://doi.org/10.1002/pamm.202400096.
Chen, T., Zhang, Y., Lin, J., Lu, Y., 2019.
Theoretical Analysis and Crashworthiness Optimization of Hybrid Multi-Cell
Structures. Thin-walled Structures, Volume 142, pp. 116–131. https://doi.org/10.1016/j.tws.2019.05.002
Cheng, J.C.,
2011. Twelve-Cornered Strengthening Member. United States, Patent No. 9533710.
Christensen, J., 2022. Efficient Crash Structure
Design for Road Traffic Accidents of Tomorrow. International Journal of
Crashworthiness, Volume 28(5), pp. 629–648. https://doi.org/10.1080/13588265.2022.2114577
Ciampaglia, A., Fiumarella, D., Niutta, C.B., Ciardiello,
R., Belingardi, G., 2021. Impact Response of an Origami-Shaped Composite Crash
Box: Experimental Analysis and Numerical Optimization. Composite Structures,
Volume 256, p. 113093. https://doi.org/10.1016/j.compstruct.2020.113093
Dimas, A., Dirgantara, T., Gunawan, L., Jusuf, A., and
Putra, I.S., 2014. The Effects of Spot Weld Pitch to the Axial Crushing
Characteristics of Top-Hat Crash Box. Applied Mechanics and Materials,
Volume 660, pp. 578–582. http://dx.doi.org/10.4028/www.scientific.net/AMM.660.578
Djamaluddin, F., 2024. Optimization of Foam-Filled
Crash-Box Under Axial Loading For Pure Electric Vehicle. Results in
Materials, Volume 21, p. 100505. https://doi.org/10.1016/j.rinma.2023.100505
Fang, J., Sun, G., Qiu, N., Kim, N. H., Li, Q., 2017. On Design Optimization
for Structural Crashworthiness and its State of the Art. Structural and
Multidisciplinary Optimization, Volume 55, pp. 1091–1119. https://doi.org/10.1007/s00158-016-1579-y
Galib, D.A., Limam, A., 2004. Experimental and
Numerical Investigation of Static and Dynamic Axial Crushing of Circular
Aluminum Tubes. Thin-walled Structures, Volume 42(8), pp. 1103–1137. https://doi.org/10.1016/j.tws.2004.03.001
Godat, A., Legeron, F., Bazonga, D., 2012. Stability
Investigation of Local Buckling Behavior of Tubular Polygon Columns Under
Concentric Compression. Thin-walled Structures, Volume 53, pp. 131–140. https://doi.org/10.1016/j.tws.2011.12.013
Gunawan, L.,
2013. Material Characterization and Axial Crushing Tests of Single and
Double-Walled Columns at Intermediate Strain Rates. Journal of Mechanical
Engineering, Volume 10(2), pp. 19–36
Halton, J.H., 1964. Algorithm 247: Radical-Inverse
Quasi-Random Point Sequence. Communications of the ACM, Volume 7(12),
pp. 701–702. https://doi.org/10.1145/355588.365104
Hou, S., Li, Q., Long, S., Yang, X., Li, W., 2007.
Design Optimization of Regular Hexagonal Thin-Walled Columns with
Crashworthiness Criteria. Finite Elements in Analysis and Design, Volume
43(6-7), pp. 555–565. https://doi.org/10.1016/j.finel.2006.12.008
Hou, W., He, P., Yang, Y., Sang, L., 2023.
Crashworthiness Optimization of Crash Box with 3D-printed Lattice Structures. International
Journal of Mechanical Sciences, Volume 247, p. 101819. https://doi.org/10.1016/j.ijmecsci.2023.108198
Hull, D., 1991. A Unified Approach to Progressive
Crushing of Fibre-Reinforced Composite Tubes. Composites Science and
Technology, Volume 40(4), pp. 377–421. https://doi.org/10.1016/0266-3538(91)90031-J
Jones, D., Schonlau, M., Welch, W., 1998. Efficient
Global Optimization of Expensive Black-Box Functions. Journal of Global
Optimization, pp. 455–492. https://doi.org/10.1023/A:1008306431147
Jongpradist, P., Tongthong, S., Kongwat, S.,
Ruangjirakit, K., Thongchom, C., Hasegawa, H., 2024. Optimizing Functionally
Graded Hexagonal Crash Boxes with Honeycomb Filler For Enhanced
Crashworthiness. Structures, Volume 59, p. 105775. https://doi.org/10.1016/j.istruc.2023.105775
Jusuf, A., Allam, F.S., Dirgantara, T., Gunawan, L.,
Putra, I.S., 2011. Low Velocity Impact Analyses of Prismatic Columns Using
Finite Element Method. Key Engineering Materials, Volume 462-463, pp.
1308–1313. http://dx.doi.org/10.4028/www.scientific.net/KEM.462-463.1308
Jusuf, A., Dirgantara, T., Gunawan, L., Putra, I.,
2015. Crashworthiness Analysis of Multi-Cell Prismatic Structures. International
Journal of Impact Engineering, Volume 78, pp. 34–50. https://doi.org/10.1016/j.ijimpeng.2014.11.011
Kholil, A., Kiswanto, G., Farisi, A. A., Istiyanto, J.,
2023. Finite
Element Analysis of Lattice Structure Model with Control Volume Manufactured
Using Additive Manufacturing. International Journal of Technology,
Volume 14(7), pp. 1428–1437. https://doi.org/10.14716/ijtech.v14i7.6660
Kumar, A.P., Maneiah, D., 2019. Deformation Studies on
the Significance of Combined Geometry Tubes as Energy Absorbing Structures. International
Journal of Civil Engineering and Technology, Volume 10(1), pp. 2812–2820.
Kumar, A.P., Sankar, L.P., Maneiah, D., Upendra, G.,
2019. Lateral Crushing and Energy Absorption Behavior of Multicellular Tube
Structures. International Journal of Innovative Technology and Exploring
Engineering, Volume 9(1), pp. 2684—2687.
http://dx.doi.org/10.35940/ijitee.A4837.119119
Liu, S., Tong, Z., Tang, Z., Liu, Y., Zhang, Z., 2015.
Bionic Design Modification of Non-Convex Multi-Corner Thin-Walled Columns for
Improving Energy Absorption Through Adding Bulkheads. Thin-walled Structures,
Volume 88, pp. 70–81.
https://doi.org/10.1016/j.tws.2014.11.006
Liu, Y., 2008. Crashworthiness Design of Multi-Corner
Thin-Walled Columns. Thin-Walled Structures, Volume 46(12), pp. 1329–1337. https://doi.org/10.1016/j.tws.2008.04.003
Liu, Y., Day, M., 2007. Development of Simplified
Finite Element Models for Straight Thin-Walled Tubes with Octagonal Cross
Section. International Journal of Crashworthiness, Volume 12(5), pp. 503–508. https://doi.org/10.1080/13588260701483557
Liu, Z., Huang, Z., Qin, Q., 2017. Experimental and
Theoretical Investigations on Lateral Crushing of Aluminum Foam-Filled Circular
Tubes. Composite Structures, Volume 175, pp. 19–27. https://doi.org/10.1016/j.compstruct.2017.05.004
Lu, Q., Deng, X., Liu, F., 2023. Crashworthiness Study
of A Novel Radial Gradient Multicell Tube. Journal of the Brazilian Society
of Mechanical Sciences and Engineering, Volume 45(8), p. 409. https://doi.org/10.1007/s40430-023-04319-2
Lu, R., Liu, X., Chen, S., Hu, X., Liu, L. 2017. Axial Crushing Analysis
for Tailor Rolled Square Tubes With Axially Graded Both Wall Thickness And
Material. Thin-walled structures, Volume 117, pp. 10–24. https://doi.org/10.1016/j.tws.2017.04.001
Mamalis, A., Manolakos, D., Ioannidis, M., Papapostolou,
D., 2004. Crashworthiness
Characteristics of Axially Statically Compressed Thin-Walled Square CFRP
Composite Tubes: Experimental. Composite Structures, Volume 63(3-4), pp.
347–360.
https://doi.org/10.1016/S0263-8223(03)00183-1
Nagarjun, J., Kumar, A.P., Reddy, K.Y., Sankar, L.P.,
2020. Dynamic Crushing and Energy Absorption Perfromance of Newly Designed
Multitubular Structures. Materials Today: Proceedings, Volume 27, pp.
1928–1933.
https://doi.org/10.1016/j.matpr.2020.04.103
Nakazawa, Y., Tamura, K., Yoshida, M., Takagi, K., Kano, M., 2005. Development of
Crash-Box for Passenger Car with High Capability for Energy Absorption.
Barcelona, VIII International Conference on Computational Plasticity.
Olabi, A., Morris, E., Hashmi, M., 2007. Metallic Tube
Type Energy Absorbers: A Synopsis. Thin-walled Structures, Volume
45(7-8), pp. 706–726.
https://doi.org/10.1016/j.tws.2007.05.003
Palar, P.S., Shimoyama, K., 2019. Kriging with
Composite Kernel Learning for Surrogate Modeling in Computer Experiments. San
Diego, California, AIAA SciTech Forum. http://dx.doi.org/10.2514/6.2019-2209
Palar, P.S., Zuhal, L.R., Shimoyama, K., 2020.
Gaussian Process Surrogate Model with Composite Kernel Learning for Engineering
Design. AIAA Journal, Volume 58(4), pp. 1864–1880. https://doi.org/10.2514/1.J058807
Pirmohammad, S., Esmaeili-Marzdashti, S., 2019. Multi-Objective
Crashworthiness Optimization of Square and Octagonal Bitubal Structures
Including Different Hole Shapes. Thin-walled structures, Volume 139, pp.
126–138.
https://doi.org/10.1016/j.tws.2019.03.004
Qi, C., Yang, S., Dong, F., 2012. Crushing Analysis
and Multiobjective Crashworthiness Optimization Of Tapered Square Tubes Under
Oblique Impact Loading. Thin-Walled Structures, Volume 59, pp. 103–119. https://doi.org/10.1016/j.tws.2012.05.008
Rasmussen, C., 2003. Gaussian Processes In Machine
Learning. In: Summer School on Machine Learning. Springer, Volume 3176,
pp. 63–71. https://doi.org/10.1007/978-3-540-28650-9_4
Reddy, S., Abbasi, M., Fard, M., 2015. Multi-Cornered
Thin-Walled Sheet Metal Members for Enhanced Crashworthiness and Occupant
Protection. Thin-walled structures, Volume 94, pp. 56–66. https://doi.org/10.1016/j.tws.2015.03.029
Reuter, C., Tröster, T., 2017. Crashworthiness and
Numerical Simulation of Hybrid Aluminium-CFRP Tubes Under Axial Impact. Thin-Walled
Structures, Volume 117, pp. 1–9.
https://doi.org/10.1016/j.tws.2017.03.034
Schneider, F., Jones, N., 2003. Influence of Spot-Weld
Failure on Crushing of Thin-Walled Structural Sections. International
Journal of Mechanical Sciences, Volume 45(12), pp. 2061–2081. https://doi.org/10.1016/j.ijmecsci.2003.11.004
Seek, C.Y., Kok, C.K., Lim, C.H., Liew, K.W., 2022. A
Novel Lattice Structure for Enhanced Crush Energy Absorption. International
Journal of Technology, Volume 13(5), pp. 1139–1148. http://dx.doi.org/10.14716/ijtech.v13i5.5829
Shahi, V., Marzbanrad, J., 2012. Analytical and
Experimental Studies On Quasi-Static Axial Crush Behavior of Thin-Walled
Tailor-Made Aluminum Tubes. Thin-walled structures, Volume 60, pp. 24–37. https://doi.org/10.1016/j.tws.2012.05.015
Skhvediani, A., Rodionova, M., Savchenko, N.,
Kudryavtseva, T., 2023. Prediction of the Road Accidents Severity Level: Case
of Saint-Petersburg and Leningrad Oblast. International Journal of
Technology, Volume 14(8), pp. 1717–1727. https://doi.org/10.14716/ijtech.v14i8.6859
Tang, Z., Liu, S., Zhang, Z., 2012. Energy Absorption
Properties of Non-Convex Multi-Corner Thin-Walled Columns. Thin-walled
structures, Volume 51, pp. 112–120. https://doi.org/10.1016/j.tws.2011.10.005
Tarigopula, V., Langseth, M., Hopperstad, O., Clausen,
A., 2006. Axial Crushing of Thin-Walled High-Strength Steel Sections. International
Journal of Impact Engineering, Volume 32(5), pp. 847–882. https://doi.org/10.1016/j.ijimpeng.2005.07.010.
Wang, W., Dai, S., Zhao, W., Wang, C., 2022.
Multi-Objective Optimization of Hexahedral Pyramid Crash Box Using Moea/D-Dae
Algorithm. Applied soft computing, Volume 118, p. 108481. https://doi.org/10.1016/j.asoc.2022.108481
Wang, Z., Jin, X., Li, Q., Sun, G., 2020. On Crashworthiness
Design of Hybrid Metal-Composite Structures. International Journal of
Mechanical Sciences, Volume 171, p. 105380. https://doi.org/10.1016/j.ijmecsci.2019.105380
White, M., Jones, N., 1999. Experimental Quasi-Static
Axial Crushing of Top-Hat and Double-Hat Thin-Walled Sections. International
Journal of Mechanical Sciences, Volume 41(2), pp. 179–208. https://doi.org/10.1016/S0020-7403(98)00047-2
Wu, S., Sun, G., Wu, X., Li, G., Li, Q., 2017. Crashworthiness
Analysis and Optimization of Fourier Varying Section Tubes. International
Journal of Non-linear Mechanics, Volume 92, pp. 41–58. https://doi.org/10.1016/j.ijnonlinmec.2017.03.001
Xu, F., Sun, G., Li, G., Li, Q., 2014. Experimental Study on
Crashworthiness Of Tailor-Welded Blank (TWB) Thin-Walled High-Strength Steel
(HSS) Tubular Structure. Thin-walled structures, Volume 74, pp. 12–27. https://doi.org/10.1016/j.tws.2013.08.021
Yamashita, M., Gotoh, M., Sawairi, Y., 2003. Axial
Crush of Hollow Cylindrical Structures with Various Polygonal Cross-Sections:
Numerical Simulation and Experiment. Journal of Materials Processing
Technology, Volume 140(1-3), pp. 59–64. https://doi.org/10.1016/S0924-0136(03)00821-5
Yuan, L., Shi, H., Ma, J., You, Z., 2019. Quasi-Static
Impact of Origami Crash Boxes with Various Profiles. Thin-Walled Structures,
Volume 141, pp. 435–446. https://doi.org/10.1016/j.tws.2019.04.028
Zhang, J., Zheng, D., Lu, B., Liu, Q., 2022. A
Numerical and Theoretical Study on Crushing Behaviours of Variable Thickness 12
Right-Angles Section Tubes. International journal of Crashworthiness,
Volume 27(1), pp. 168–180. https://doi.org/10.1080/13588265.2020.1784538
Zhang, X., Huh, H., 2010. Crushing Analysis of
Polygonal Columns and Angle Elements. International Journal of Impact
Engineering, Volume 37(4), pp. 441–451. https://doi.org/10.1016/j.ijimpeng.2009.06.009
Zhang, X., Wen, Z., Zhang, H., 2014. Axial Crushing
and Optimal Design of Square Tubes With Graded Thickness. Thin-walled
Structures, Volume 84, pp. 263–274. https://doi.org/10.1016/j.tws.2014.07.004
Zhang, X., Zhang, H., 2012. Experimental and Numerical
Investigation on Crush Resistance of Polygonal Columns and Angle Elements. Thin-walled
Structures, Volume 57, pp. 25–36. https://doi.org/10.1016/j.tws.2012.04.006
Zhang, X., Zhang, H., Yang, C., Leng, K., 2019. Static
and Dynamic Axial Crushing of Self-Locking Multi-Cell Tubes. International
Journal of Impact Engineering, Volume 127, pp. 17–30. https://doi.org/10.1016/j.ijimpeng.2019.01.002
Zhou, C., Zhou, Y., Wang, B., 2017. Crashworthiness
Design for Trapezoid Origami Crash Boxes. Thin-walled Structures, Volume
117, pp. 257–267. https://doi.org/10.1016/j.tws.2017.03.022
