The Effect of Fiber Orientation and Crack on Dynamic Characteristics of a Unidirectional Composite Cantilevered Wing Plate
Corresponding email: sasongko@ae.itb.ac.id
Published at : 24 Dec 2024
Volume : IJtech
Vol 15, No 6 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i6.7228
Ramadhan, F., Sasongko, R.A., Gunawan, L., Akbar, M., Widagdo, D., 2024. The Effect of Fiber Orientation and Crack on Dynamic Characteristics of a Unidirectional Composite Cantilevered Wing Plate. International Journal of Technology. Volume 15(6), pp. 1663-1677
| Faisal Ramadhan | Departement of Aerospace Engineering, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Kampus Ganesha, Bandung 40132, Indonesia |
| Rianto Adhy Sasongko | Departement of Aerospace Engineering, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Kampus Ganesha, Bandung 40132, Indonesia |
| Leonardo Gunawan | Departement of Aerospace Engineering, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Kampus Ganesha, Bandung 40132, Indonesia |
| Mahesa Akbar | College of Business, Technology, and Engineering, Sheffield Hallam University, City Campus, Howard Street, Sheffield S1 1WB, United Kingdom |
| Djarot Widagdo | Departement of Aerospace Engineering, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Kampus Ganesha, Bandung 40132, Indonesia |
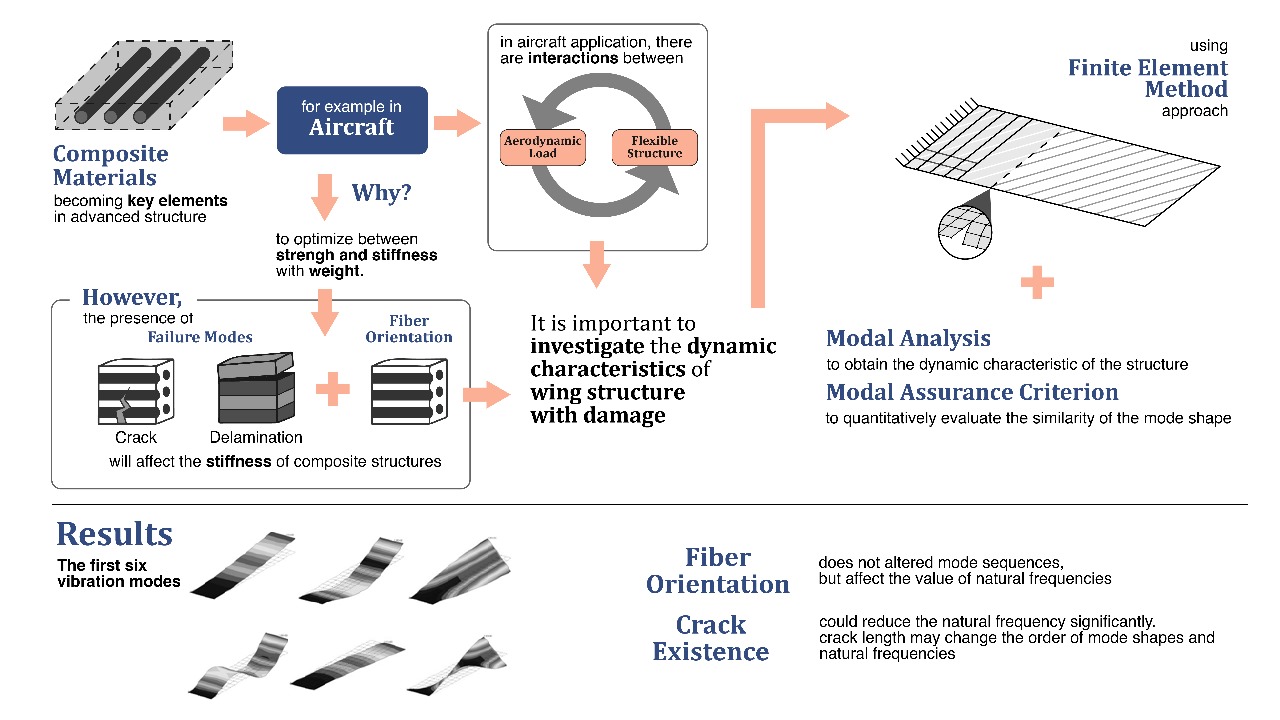
Composite materials are becoming key elements in constructing advanced structures such as aircraft. These structures offer the benefit in terms of optimization between strength, stiffness, and weight. In recent studies, the concern of composite structures applications is the understanding of their failure modes such as crack and delamination, including complex fiber orientations. The presence of crack with various fiber orientations may affect the stiffness of the structure. In aircraft applications, particularly wing structures, the issue is more challenging due to the coupling of aerodynamic load and flexible structure which leads to aeroelastic phenomenon of flutter. Therefore, this study aimed to investigate the effect of crack on dynamic characteristics of a unidirectional composite simplified wing-like structure. The experiment was conducted by constructing the finite element model of a simplified wing-like structure as the basis, which was modeled as a unidirectional composite plate structure with some predefined fiber directions. To model the damage, a chordwise crack was inserted into the structure, whose length and location could be varied. Modal analysis was conducted to obtain dynamic characteristics of the composite structure, namely natural frequencies and mode shapes. The changes in natural frequencies and mode shapes for different combinations of fiber directions, crack lengths, and crack locations, are quantified and analyzed. Modal Assurance Criteria (MAC) was used to quantitatively evaluate the similarity of the mode shapes for different fiber orientation settings. The results showed that the order of the first six vibration modes, namely bending and torsion, was not altered by the change of fiber orientations but affected the value of natural frequencies. Furthermore, the existence of crack could reduce the natural frequencies significantly. MAC evaluation also showed that crack length could change the order of the mode shapes and the natural frequency of particular modes. For the fundamental modes, first bending and torsion, the natural frequencies decrease by approximately 20% as crack moves closer to the root. The changes in natural mode order and frequencies influenced the occurrence of couplings between modes capable of affecting the stability boundary in aeroelastic case.
Composite; Dynamic haracteristics; Finite element method; Mode shape; Modal assurance criteria; Natural frequency
The use of composite materials in high-performance applications is growing significantly in recent decades (Warren, 2004). Composite materials enable the optimization of the mechanical performance of the structures, namely stiffness, strength, and weight reductions (Dursun and Soutis, 2014). In other applications, composite is also used for noise and vibration controls (Zulkarnain et al., 2024). Recently, in aerospace industry, composite materials in the form of carbon fiber reinforced polymers (CFRPs), have been used to construct the main component of aircraft structures (Galos, 2020). As an example, more than 50% airframe structures of Boeing 787 (Hale, 2006) and Airbus A350 XWB (Kinsley-Jones, 2006) are made of CFRPs. Despite their growing application, composite structures in aircraft are still concerned with distinct types of failure, particularly delamination and crack (Purnowidodo et al., 2018).
In aircraft applications, the operating conditions exert complex combined load cases, such as the interaction between aerodynamic and structural dynamic loads (Wright and Cooper, 2015; Bisplinghoff and Ashley, 2013; ESDU, 2004). One of the cases concerning the incident of crack and aero-structure interaction has been reported by the National Transportation Safety Board (NTSB, 2012). A racing aircraft experienced a structural failure which caused control loss and collision with airport ground, leading to fatal injuries on the pilot and people on the ground. From the investigation, it was found that the fatigue crack in one of the elevator’s screws caused stiffness reduction of the elevator system leading to flutter in the aircraft normal racing’s speed range. Flutter is one of aeroelastic phenomena that occurs when two or more vibration modes are coupled by unsteady aerodynamic forces, leading to damping loss and dynamic instability (Hoseini and Hodges, 2019a; Hodges and Pierce, 2011). The incident has shown the importance of the interaction between fracture mechanics and aeroelasticity, known as aerofracturelasticity (Abdullah, Curiel-Sosa, Akbar, 2018). These two fields interact as aerodynamic load induces the initiation and propagation of crack causing changes in load distribution on the structure. Crack reduces the stiffness of the structure, which increases the deflection and the stress levels. The low stiffness also decreases the natural frequencies and aeroelastic instability speed inducing a high dynamic stress level. This higher stress level increases crack size, which continues in a loop leading to the occurrence of aeroelastic instability in the flight envelope of the aircraft. According to a previous study, the stiffness significantly affects the flutter boundary (Torabi et al., 2021; Castravete and Ibrahim, 2008).
One of the earliest studies on aerofracturelasticity of composite structure was discussed in (Strganac and Kim, 1996), investigating panel and bending-torsion flutter for cantilevered composite plate. The results showed that aeroelastic responses are dependent on the distribution of damage. (Pidaparti and Chang, 1998; Pidaparti, 1997) also described that the free vibration and flutter characteristics of composite plates were influenced by the existence of damage. However, these previous studies (Pidaparti and Chang, 1998; Pidaparti, 1997; Strganac and Kim, 1996) only investigated aeroelastic phenomena in a supersonic regime as aerodynamic models used piston theory which was more appropriate for analytical approaches.
Wang et al. investigated aeroelastic flutter and divergence speed limits for damaged composite in the subsonic regime. Unidirectional composite plates with various fiber directions, elastic axis, crack locations, and lengths were also evaluated (Wang et al, 2005a). The composite plate structure was represented using a composite beam while aerodynamic load was modeled with 2D quasi-steady strip theory. Similar to Strganac (Strganac and Kim, 1996), the edge crack was represented using a reduced stiffness modulus property. Abdullah (Abdullah et al., 2019) studied crack behavior of unidirectional composite plates using XFEM under aeroelastic gust loads, where the structure model was represented with 3D elements, and aerodynamic load was shown by the Doublet Lattice Method (DLM). Finite Element Method (FEM) coupled with fluid dynamics or aerodynamics solver has been well established for use in complex configurations such as wing with advanced materials (Akbar et al., 2022) or wind turbine blade (Hamza et al., 2023). Another study by Hoseini and Hodges examined the linear and nonlinear divergence as well as flutter of damaged high-aspect-ratio composite wings (Hoseini and Hodges, 2019b).
Despite the elaborated efforts in the study of aerofracturelasticity of composite, there is a lack of discussion on the effect of crack on structural dynamic characteristics of the structure before aeroelastic instability evaluation (Sharma et al., 2023; Wang et al., 2023). Previous studies had discussed the structural dynamics of the damaged composite plate (Wang et al., 2005b). The results showed that the bending and torsion natural frequencies for composite with a particular fiber direction could coupled due to crack. This shows the need to consider the effect of fiber orientations and the presence of crack on the natural frequencies and the mode shapes of a structure. This process is essential to obtain a comprehensive picture of dynamic characteristics of composite structures, thereby addressing instability phenomena such as flutter and divergence. Although a few studies have been published on this topic, the influence of crack presence on dynamic characteristics of a structure was not thoroughly explored.
Based on the description, this study aimed to explore the effect of crack on dynamic characteristics of simple wing structures using FEM (MSC Software Corporation, 2009; Cook et al., 2001). To minimize the complexity, the study was carried out for a wing model in the form of a cantilevered unidirectional composite plate, focusing on static crack without any propagation. Parametric analyses were carried out to evaluate the effect of varying crack sizes and locations on the wing with several fiber orientations.
2.1. Finite Element Model and Validation
The cantilevered wing model used in this study referred to the composite plate discussed by Wang and Abdullah, as shown in Figure 1.a (Abdullah et al., 2018; Wang et al., 2005a). The chord length, c, is 100 mm, the wingspan, L, is 500 mm, and the thickness, h, is 5 mm. Fiber orientation, as represented in green in Figure 1.a, is measured from the mid-chord of the wing with 1-axis representing the direction of fibers and 2-axis showing the direction perpendicular to fibers on x-y plane. The angle of indicates that fibers are in line with the x-axis. The location of crack, as represented in blue in Figure 1.a, measured from wing root and its length, are indicated with l and a, respectively.
The modelling of cantilevered wing was conducted using shell elements with a rectangular mesh of 20×25 mm, as shown in Figure 1.b. The mesh size followed the increments of the length in chord direction and the location of crack in span direction. Based on the mesh size, the total number of elements used in this model was 100. To replicate the behavior of a cantilevered wing, fixed boundary conditions were applied at the root of the wing. The use of shell elements provides an advantage in modeling crack as a slit on the wing surface (Georgiou, Manan, and Cooper, 2012). Additionally, at crack location, there is a duplication of nodes to replicate the physical condition of crack. In comparison, (Wang et al., 2005b) conducted wing modeling by using beam elements and crack was represented by a reduced stiffness modulus property. This refined method ensures a more accurate representation of crack’s influence on dynamic characteristics of composite wing structure.
Dynamic characteristics of the wing with fiber directions of is used as the baseline model. Parametric studies are performed by varying fiber direction for the undamaged wing and by varying crack position and size for the 0° fiber orientation wing. Subsequently, the results are analyzed by comparing with the baseline model. Fiber orientation is varied from 0o to 135o with 15o increments. For the variation of crack parameters, crack length, which further is called as
is varied from 0.2 to 0.8 span with 0.2 increments. Crack location, which is expressed as
is varied from 0.2 to 0.8 with 0.1 increment. The material properties of the composite and their constitutive values are provided in Table 1 (Abdullah et al., 2018; Wang et al., 2005a).
Figure 1 Structural modeling with (a) general parameters and (b) finite element model.
2.1. Modal Analysis and Modal Assurance Criteria
Modal analysis examines dynamic characteristics of a structure in the frequency domain. This analysis uses the structure's overall mass and stiffness to determine the natural frequencies at which the structure will resonate. Modal analysis includes solving the eigenproblem as shown in Equation 1 (MSC Software Corporation, 2009). The natural frequencies () are obtained as the eigenvalues, while the eigenvectors represent the corresponding mode shapes
Fiber orientations and the presence of crack affect the mode shapes, while the corresponding natural frequencies obtained from the modal analysis (Tsunematsu and Donadon, 2019; Lee et al., 2016; Honda and Narita, 2012). The effect of each parameter on the natural frequencies is analyzed through comparison with the natural frequency of the baseline model (the 0? undamaged model) with similar or almost similar shapes. The similarity of the two modes is quantified using Modal Assurance Criteria (MAC) (Gres, Döhler, and Mevel, 2021; Allemang, 2003).
MAC measures the collinearity between two mode shape vectors and its value is a real scalar ranging from 0 to 1. The value of 0 indicates that the two modes are not similar and 1 shows very similar. The value of MAC of the two modes is determined using Eq. 2, where represents the mode shape matrix with the size of 1×n. In this equation, n is the number considered nodes, the subscript r denotes the reference, c represents the comparison, and the asterisk signifies the complex conjugate of the mode shape.
Table 1 The value of (a) composite properties and (b) constitutive values
3.1. Validation of the Baseline Model
Initially, analysis is carried out on dynamic characteristics of the undamaged wings with 0° fiber direction, designated as the baseline model in the parametric studies. For this baseline model, the results obtained from modal analysis are presented and compared with the referenced work, as shown in Table 2. The overall relative errors obtained from the comparisons are below 2%. The model is validated and can be used to perform further study. Based on the mesh convergence test on the first bending mode in Figure 2, the result shows that the number of elements used in this study, which is 100, is converged relative to the higher number of elements.
Table 2 Modal analysis results comparison.
Figure 2 Mesh Convergence of the First Bending Mode Natural Frequency.
The modes of the baseline model are sorted based on the increasing order of the natural frequencies, as shown in Table 2 and Figure 3. The comparisons of dynamic characteristics obtained from this study with the reference are conducted through visual judgment to make sure that each matching frequency has the same mode shapes. The first six mode shapes of 0° undamaged wing sequentially include first bending (1B), second bending (2B), first torsion (1T), third bending (3B), first swaying (1S), and second torsion (2T). These vibration modes notation will be used in further discussion. For a wing with a different fiber orientation or damage, dynamic characteristics results sorted by considering the increasing values of natural frequencies show different order of mode shapes. Therefore, MAC values of modes obtained from each baseline model are calculated to identify two modes with similar shapes. After the identification of the two similar modes, the change in the natural frequency of mode can be determined.
Figure 3 The first six mode shapes: (a) 1B, (b) 2B, (c) 1T, (d) 3B, (e) 1S, and (f) 2T.
3.2. The Effect of Fiber Orientations on Dynamic Characteristics of the Undamaged Wing
Figure 4 The value of MAC for modes of (a) 0°, (b) 30°, and (c) 45°fiber orientation case relative to the baseline modes (cont.).
Figure 4 The value of MAC for modes of (a) 0°, (b) 30°, and (c) 45°fiber orientation case relative to the baseline modes (cont.).
Figure 4 shows MAC of the 6 modes obtained from the wing with 0°, 30°, and 45° fiber orientation calculated relative to the baseline model. The results show that MAC between the modes in each case and baseline model are maximum in the diagonal position. This indicates that the first mode of each case corresponds to the baseline model and for other vibrations. Similar results are also obtained for wings with other fiber directions. The variations of fiber orientations in this study do not affect the sequence of vibration modes compared to the baseline.
Figure 5 (a) The color map of MAC value regarding the varying fiber orientations in the first six mode shapes (b) Visual comparison between 0o and 90o orientations modes
After determining the mode sequences for each case, the effect of fiber direction on the geometric similarity of the mode shapes can be evaluated. Figure 5.a shows the highest MAC values of the modes related to the baseline model for each case. For all fiber orientations, including the first and the fifth modes, namely first bending and first in-plane bending, MAC is 1. This indicates that the shape of modes for each case is the same as baseline. All modes of the 90? fiber orientation wing have the same shape as baseline. This is confirmed by Figure 5.b, showing that the first three modes of wing with 90o are the same as baseline.
Figure 6 (a) The graph of natural frequency vs. fiber angle for the first six modes (b) The comparison of the first four natural frequencies of the undamaged model with fiber angle variation to prior work
The changes in natural frequencies of the wing due to different fiber orientations are shown in Figure 6.a. The frequency of each mode shape fluctuates as fiber orientation is changed from 0o to 90?, which is more pronounced at higher values. For varying fiber orientation from 0o to 45o, each natural frequency increases or decreases, reaching a maximum or minimum at 45o. Subsequently, from 45o to 90o, each natural frequency goes in the opposite direction and reaches the same value at 90o as baseline wing (0o). For this wing model, the span-wise bending stiffness of fiber orientation at 90o is the same as baseline wing (C11=C22).
The results show that fiber orientation affects dynamic characteristics of the wing as shown by MAC in Figure 5.a and the natural frequencies in Figure 6.a. Special fiber orientations observed in this study are 45o and 90o. The wing with fiber orientation of 45o has the largest difference with baseline while the mode shapes are similar to baseline wing. For wing with fiber orientation of 90o, the natural frequencies and the mode shapes are the same as baseline wing.
Figure 6.a shows that the natural frequency curves do not cross each other. This confirms that the mode shape sequence of the wing is unchanged with varying fiber orientation. However, (Wang et al., 2005a) found that there was an alteration of the mode shape sequence as shown in Figure 6.b. These differences occur due to the modeling method, as Wang used beam elements and incorporated fiber angles into the stiffness matrix.
3.3. The Effect of Crack on Dynamic Characteristics of Wing
In this step, eigenvalue analyses are carried out for wing with 0° fiber orientation comprising crack at position varying from =0.2 to 0.8 with 0.2 increment. For each position, crack size varies from
=0.2 to 0.8 , with 0.1 increment. Eigenvectors for each case are analyzed following the same procedure as in the previous section.
Figure 7 The value of MAC relative to the baseline modes for and
The presence of crack can change the sequence of mode-shapes. Figure 7.a shows the maximum MAC between modes of wing with crack compared to baseline model for crack at position =0.2 and size
=0.2. In this case, MAC of modes of wing referred to the baseline modes, as shown in Figure 7.a. This indicates that for fourth and fifth, mode shapes are similar to baseline modes, respectively. The values of the maximum MAC are mostly less than 1, showing that the corresponding modes have slightly different shapes. Based on the results, eigensolutions of this wing can be re-sequenced according to the mode's similarity with baseline model. Figure 7.b shows that the presence of crack at the same position but with larger size,
=0.4, changes the sequence of modes and similarity of the shapes.
After determining the maximum MAC values and resequencing the eigensolutions based on their similarity to the baseline modes, the impact of cracks on the mode shapes can be analyzed. This report focuses on the first four mode shapes. Figure 8.a shows the maximum MAC values for all cases corresponding to the first baseline mode (1B). A maximum MAC value of 1 indicates that the geometry of the 1B mode remains unchanged regardless of the presence of crack. Figure 8.b shows the maximum MAC values for modes most similar to the second baseline mode (2B). For crack lengths less than 0.4c, MAC values are 1, suggesting that crack smaller than 0.4c does not alter the shape of the 2B mode. However, a larger crack closer to the wing root alters the shape of the 2B mode. As shown in Figure 8.c, the maximum MAC values for modes are most similar to the third baseline mode (1T). For crack lengths under 0.4c, MAC values are 1, indicating no change in the 1T mode shape for smaller cracks. A larger crack near the wing root modifies the 1T mode shape. Figure 8.d presents the maximum MAC values for modes most similar to the fourth baseline mode (3B). Crack smaller than 0.4c do not alter the 3B mode shape, as shown by MAC value of 1. A larger crack closer to 0.6L significantly changes the 3B mode shape.
Figure 9.a shows the natural frequency of the wing for crack position at =0.2 with varying lengths. In this case, increasing crack length lowers the natural frequencies. The most affected mode is the 1T, where its natural frequencies are significantly reduced and close to the 2B for crack size of 0.8c. Figure 9.b shows the natural frequency of the wing for crack length of
=0.2 and varying positions. In this case, crack location does not significantly affect the natural frequencies of all modes.
To provide more complete information on the effect of the presence of crack, the values of natural frequencies of mode at each position and size are tabulated and given a color map according to their magnitude, as shown in Table 3. Lighter colors are related to lower frequencies and vice versa. The table shows that the natural frequency of the first bending mode decreases as crack location reaches the wing root, along with an increase in crack length. This pattern is similarly shown for the first torsion mode. For the second bending mode, the natural frequency reaches its minimum value around the half-span of the wing. Additionally, for the third bending mode, the natural frequency decreases as crack length increases, with the lowest value occurring at approximately 0.3L and 0.7L.
Figure 8 The color map of MAC value for the first four modes: (a) 1B, (b) 2B, (c) 1T, and (d) 3B
The changes in the natural frequencies and mode shapes due to the presence of crack are correlated. For the 1B modes, their shapes are not affected by the presence of crack, as shown by MAC values of 1 in Figure 8.a. The natural frequencies do not vary significantly with minimum values occurring for as shown in Table 3. For the 2B, the lowest MAC occurs for
=0.2 while the lowest natural frequency occurs for
=0.5 in each crack length. Slight significant effects are observed for the 1T mode where MAC values are close to 1 and the natural frequencies do not vary significantly with minimum values occurring at 0.8 and
=0.2. For the 3B, the lowest MAC occurs for
=0.2 and
=0.6 for more than 0.4 while the lowest natural frequency occurs for
=0.3 and
=0.7. The results may shift when the analysis is carried out with finer increment of crack position size.
Figure 9 The natural frequency values for (a) =0.2 with crack length variation and (b)
=0.2 with crack location variation
The reason why certain crack locations significantly affect dynamic characteristics can be explained by using Figure 10 which shows the mode shapes for first three bending modes. The 1B mode has the lowest natural frequency when crack location is close to the wing root with the largest stress and strain during vibrations. A similar explanation may also apply to the 1T mode. The 2B mode has the lowest natural frequency values for crack position in the neighborhood of the half-span region, the antinode position which correlates with high stress and strain. Similarly, the 3B mode has the lowest natural frequency values for crack position close to the antinodes at 0.3L and 0.7L. These results show that the location of crack near the antinode significantly affects the natural frequency.
Table 3 The value of natural frequencies in several and
Figure 10 The bending mode shapes normalized displacements of undamaged wing model
In conclusion, a novel investigation of the effect of crack on the structural dynamic characteristics of unidirectional wing-like composite plate was conducted using FEM. Fundamental bending and torsional modes were also evaluated during the analysis. Quantitative analysis using MAC was implemented to compare the mode shapes of different fiber orientations. Despite the change in natural frequencies specifically composite with 45° orientation, variations on fiber orientation showed insignificant changes in the mode shape pattern. The mode shapes of the composite plate with various crack configurations, namely lengths and locations, were also compared through MAC. The variations in crack length caused a significant reduction in the mode shapes compared to baseline plate. The similarity of the 2B and 1T modes of the damaged plate was reduced by 12-13% compared to baseline. In addition, fundamental modes, namely the 1B and 1T modes had approximately 20% natural frequency reduction when crack was located near the root. Higher-order modes, such as the 2B and 3B modes, had the largest natural frequency reduction when crack was near the antinode of the respective mode. In this case, as the modes were changed and the frequencies reduced, the bending and torsion modes could approximately be coupled even before the existence of aerodynamic loads. Therefore, there might be shifting in the critical aeroelastic boundaries when the composite plate was exposed to airflow.
The authors are grateful for the funding provided through the ITB Research, Community Service, and Innovation Program (P2MI ITB) 2023 based on FTMD Dean’s Letter Number 24E/IT1.C04/SK-KP/2023.
Conflict of Interest
Disclose any conflicts of interest, or explicitly state "The authors declare no conflicts of interest." Authors are required to disclose and acknowledge any personal circumstances or interests that may be perceived as inappropriately influencing the representation or interpretation of the research results.
Abdullah, N.A., Curiel-Sosa, J.L., Akbar, M., 2018. Aeroelastic
Assessment of Cracked Composite Plate by Means of Fully Coupled Finite Element
and Doublet Lattice Method. Composite
Structures, Volume 202, pp. 151–16. https://doi.org/10.1016/j.compstruct.2018.01.015
Abdullah, N.A., Akbar, M., Wirawan, N., Curiel-Sosa, J.L., 2019.
Structural Integrity Assessment on Cracked Composites Interaction with
Aeroelastic Constraint by Means of XFEM. Composite
Structures, Volume 229, p. 111414. https://doi.org/10.1016/j.compstruct.2019.111414
Akbar, M., Abdullah, N.A., Hadian, M., 2022. Evaluation on
Piezoaeroelastic Energy Harvesting Potential of A Jet Transport Aircraft Wing
with Multiphase Composite by means of Iterative Finite Element Method. International Journal of Technology,
Volume 13(4), pp. 803–815
Allemang, R.J., 2003. The Modal Assurance Criterion (MAC): Twenty
years of Use and Abuse. Sound and
Vibration, Volume 37 (8), pp. 14–21. https://doi.org/10.14716/ijtech.v13i4.5468
Bisplinghoff, R.L., Ashley, H., 2013. Principles of Aeroelasticity. New York: John Wiley & Sons
Castravete, S.C., Ibrahim, R.A., 2008. Effect of Stiffness
Uncertainties on the Flutter of a Cantilever Wing. AIAA Journal, Volume 46(4), pp. 925–935. https://doi.org/10.2514/1.31692
Cook, R.D., Malkus, D.S., Plesha, M.E., Witt, R.J., 2001. Concepts and Applications of Finite Element
Analysis, 4th Edition. Wiley. https://doi.org/10.1115/1.3264300
Dursun, T., Soutis, C., 2014. Recent Developments in Advanced
Aircraft Aluminium Alloys. Materials and
Design, Volume 56, pp. 862–871. https://doi.org/10.1016/j.matdes.2013.12.002
ESDU, 2004. ESDU 04024: An
Introduction to Rigid Aeroplane Response to Gusts and Atmospheric Turbulence.
ESDU
Galos, J., 2020. Thin-ply Composite Laminates: a Review. Composite Structures, Volume 236, p.
111920. https://doi.org/10.1016/j.compstruct.2020.111920
Georgiou, G., Manan, A., Cooper, J.E., 2012. Modeling Composite
Wing Aeroelastic Behavior with Uncertain Damage Severity and Material
Properties. Mechanical Systems and Signal
Processing, Volume 32, pp. 32–43. https://doi.org/10.1016/j.ymssp.2012.05.003
Gre?, S., Döhler, M., Mevel, L., 2021. Uncertainty quantification
of the Modal Assurance Criterion in Operational Modal Analysis. Mechanical Systems and Signal Processing,
Volume 152, p. 107457. https://doi.org/10.1016/j.ymssp.2020.107457
Hale, J., 2006. Boeing 787 from the Ground Up. Boeing Aero Magazine, pp. 1–10
Hamza, S., Heidari, M., Ahmadizadeh, M., Dashtizadeh, M., Chitt,
M., 2023. Modification of Horizontal Wind Turbine Blade: A Finite Element
Analysis. International Journal of
Technology, Volume 14(1), pp. 5–14. https://doi.org/10.14716/ijtech.v14i1.5255
Hodges, D.H., Pierce, G.A., 2011. Introduction to Structural Dynamics and Aeroelasticity. Cambridge
University Press. https://doi.org/10.1017/CBO9780511997112
Honda, S., Narita, Y., 2012. Natural Frequencies and Vibration
Modes of Laminated Composite Plates Reinforced with Arbitrary Curvilinear Fiber
Shape Paths. Sound and Vibration,
Volume 331, pp. 180–191. https://doi.org/10.1016/j.jsv.2011.08.019
Hoseini, H.S., Hodges, D.H., 2019a. Nonlinear Flutter and
Limit-Cycle Oscillations of Damaged Highly Flexible Composite Wings. Nonlinear Dynamics, Volume 97, pp. 247–268. https://doi.org/10.1007/s11071-019-04968-w
Hoseini, H.S., Hodges, D.H., 2019b. Aeroelastic Stability Analysis
of Damaged High-Aspect-Ratio Composite Wings. Journal of Aircraft, Volume 56(5), pp. 1794–1808. https://doi.org/10.2514/1.C035098
Kinsley-Jones, M., 2006. Airbus's A350 Vision Takes Shape—Flight
Takes an In-Depth Look at The New Twinjet. Flight
International, pp. 1–10
Lee, T.-H., Kim, J.-H., Lee, J.-H., Lee, S.-K., 2016. Effect of
Fiber Orientation on Acoustic and Vibration Response of a Carbon Fiber/Epoxy
Composite Plate: Natural Vibration Mode And Sound Radiation. Sound and Vibration, Volume 117, pp.
162–173. https://doi.org/10.1016/j.ijmecsci.2016.08.023
MSC Software Corporation, 2009. MSC.Nastran Version 68. Aeroelastic Analysis User's Guide.
MSC.Software Corporation
NTSB, 2012. Aircraft
Accident Brief - Pilot/Race 177, the Galloping Ghost, North American p-51d,
n79111, Reno, Nevada, September 16, 2011. NTSB/AAB-12/01. National
Transportation Safety Board
Pidaparti, S., Chang, J., 1998. Finite Element Supersonic Flutter
Analysis of Skewed And Cracked Composite Panels. Computers and Structures, Volume 69, pp. 265–270. https://doi.org/10.1016/S0045-7949(98)00003-0
Pidaparti, R., 1997. Free Vibration and Flutter of Damaged
Composite Panels. Composite Structures,
Volume 38(1-4), pp. 477–481. https://doi.org/10.1016/S0263-8223(97)00082-2
Purnowidodo, A., Anam, K., Darmadi, D.B., Wahjudi, A., 2018. The
Effect of Fiber Orientation and Stress Ratio on The Crack Growth Behavior of
Fiber Metal Laminates (FMLs). International
Journal of Technology, Volume 9(5), pp. 1039–1048. https://doi.org/10.14716/ijtech.v9i5.853
Sharma, N., Mohapatra, S., Kumar, E.K., Panda, S.K., 2023.
Numerical Aeroelastic Flutter Prediction of Variable Stiffness Laminated Panels
with Curvilinear Fiber in Supersonic Flow. Structures,
Volume 57, p. 105198. https://doi.org/10.1016/j.istruc.2023.105198
Strganac, T.W., Kim, Y.I.,
1996. Aeroelastic Behavior of Composite Plates Subject to Damage Growth. Aircraft, Volume 33, pp. 638–673. https://doi.org/10.2514/3.46904
Torabi, A.R., Shams, S., Narab, M.F., Atashgah, M.A., 2021.
Unsteady Aero-Elastic Analysis of A Composite Wing Containing an Edge Crack. Aerospace Science and Technology, Volume
115, p. 106769. https://doi.org/10.1016/j.ast.2021.106769
Tsunematsu, D.Q., Donadon, M.V., 2019. Aeroelastic Behavior of
Composite Panels Undergoing Progressive Damage. Composite Structures, Volume 210, pp. 458–472. https://doi.org/10.1016/j.compstruct.2018.11.065
Wang, K., Inman, D.J., Farrar, C.R., 2005a. Crack-Induced Changes
in Divergence and Flutter of Cantilevered Composite Panels. Structural Health
Monitoring, Volume 4(4), pp. 377–392
Wang, K., Inman, D.J., Farrar, C.R., 2005b. Modeling and Analysis
of a Cracked Composite Cantilever Beam Vibrating in Coupled Bending and
Torsion. Sound and Vibration, Volume
284, pp. 23–49. https://doi.org/10.1177/1475921705057977
Wang, J., Zhou, L., Chen, L., Song, M., Yang, J., Kitipornchai, S.,
2023. Aeroelastic Flutter of Actively Controlled Nanocomposite Beams with an
open Edge Crack. Aerospace Science and
Technology, Volume 141, p. 108498. https://doi.org/10.1016/j.ast.2023.108498
Warren, A., 2004. Developments and Challenges for Aluminum – A
Boeing Perspective. In: 9th
International Conference on Aluminium Alloys, pp. 24-31
Wright, J.R., Cooper, J.E., 2015. Introduction to Aircraft Aeroelasticity and Loads, 2nd Edition.
John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118700440.ch6
Zulkarnain, M., Harny, I., Insdrawaty, M.I., Azman, M.I.F., Azmi,
M.I.A., Kusrini, E., 2024. Study on Nature Fiber Composite for Noise Material
Control. International Journal of
Technology, Volume 15(3), pp. 618–627. https://doi.org/10.14716/ijtech.v15i3.6442
