Impact of Mahalanobis-Taguchi System on Health Performance Among Academicians
Corresponding email: myazid@umpsa.edu.my
Published at : 28 May 2025
Volume : IJtech
Vol 16, No 3 (2025)
DOI : https://doi.org/10.14716/ijtech.v16i3.7226
Halim, NAM, Abu, MY, Razali, NS, Aris, NH , Sari, E , Jaafar, NN, Ghani, ASA, Ramlie, F, Muhamad, WZAW & Harudin, N 2025, ‘Impact of mahalanobis-taguchi system on health performance among academicians’, International Journal of Technology, vol. 16, no. 3, pp. 846-864
| Nur Aisyah Mardhiah Halim | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Mohd Yazid Abu | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Nor Suhadah Razali | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Nurul Haziyani Aris | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Emilia Sari | Universitas Trisakti, Faculty of Industrial Technology, Department of Industrial Engineering, 11440 Kyai Tapa No 1, West Jakarta, Indonesia |
| Nur Najmiyah Jaafar | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Ahmad Shahrizan Abdul Ghani | Faculty of Manufacturing and Mechatronic Engineering Technology, Universiti Malaysia Pahang Al-Sultan Abdullah, 26600 Pekan, Pahang, Malaysia |
| Faizir Ramlie | Razak Faculty of Technology and Informatics, Department of Mechanical Engineering, Universiti Teknologi Malaysia, Jalan Sultan Yahya Petra, 54100 Kuala Lumpur, Malaysia |
| Wan Zuki Azman Wan Muhamad | Institute of Engineering Mathematics, Universiti Malaysia Perlis, Kampus Pauh Putra, Perlis 02600 Arau, Malaysia |
| Nolia Harudin | Department of Mechanical Engineering, Universiti Tenaga Nasional, 43000 Kajang, Selangor, Malaysia |
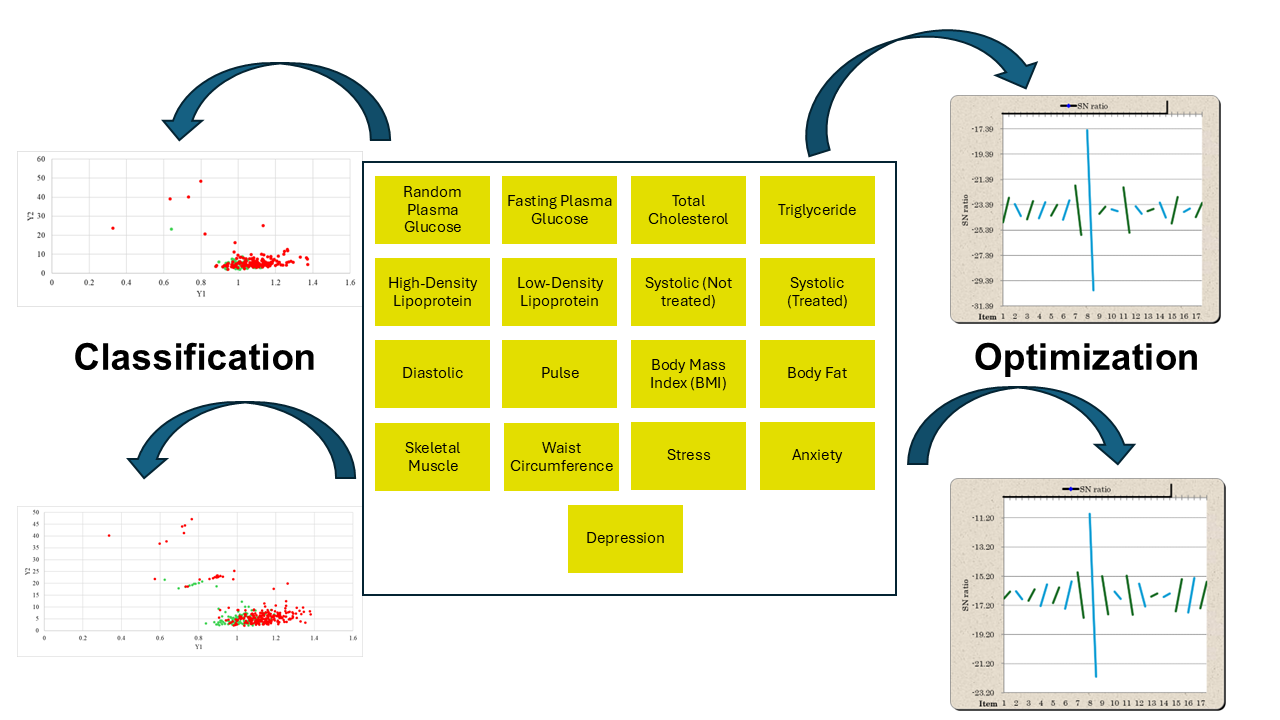
Health performance generally refers to the effectiveness and efficiency of individual or population health outcomes and behaviors. It comprises various aspects, such as physical health, specifically how well an individual manages disease and engages in preventive measures, as well as mental health. Non-communicable diseases affect individuals across diverse backgrounds and regions globally. Therefore, this study aimed to investigate the impact of Mahalanobis-Taguchi System (MTS) on health performance among academicians. Data were collected from health center that served all academic faculties at a local university, focusing on the years 2022 and 2023. To achieve the objective, a total of 17 parameters were considered. The robust Taguchi (RT) Method was used for classification, while the Taguchi (T) Method was used for optimization. In 2022, Mahalanobis distance for abnormal cases ranged between a minimum of 0.0130 and a maximum of 49.9425. For normal cases, the distance ranged between 0.0176 and 44.5121, with a total of 48 samples overlapping the threshold. In 2023, the distance ranged between 0.012843 and 36.986225 for abnormal cases. Meanwhile, for normal cases, the distance ranged between 0.002879 and 8.405225, with a total of 122 samples overlapping the threshold. For both 2022 and 2023, the data for normal and abnormal cases showed a strong negative correlation, with values of -0.6161, -0.3636, -0.5921, and -0.6252, respectively. Regarding the degree of contribution, seven parameters, namely fasting plasma glucose, untreated systolic blood pressure, treated systolic blood pressure, pulse, body mass index (BMI), body fat, and waist circumference, showed a positive degree of contribution in 2022. In 2023, ten parameters, including random plasma glucose, fasting plasma glucose, untreated systolic blood pressure, treated systolic blood pressure, diastolic blood pressure, pulse, BMI, body fat, skeletal muscle, and waist circumference, showed a positive degree of contribution. Therefore, MTS is a valuable tool for evaluating health performance among academicians, offering robust classification and optimization capabilities.
Classification; Health performance; Optimization; RT Method; T Method
Noncommunicable Diseases (NCDs) affect people worldwide, spanning a variety of backgrounds and geographical locations. The common occurrence of NCDs in individuals, families, and communities causes serious health effects. In the twenty-first century, treating and controlling these diseases has become an essential development requirement. Globally, NCDs continue to be the leading cause of disease burden, accounting for 74% of all deaths (approximately 41 million) in 2019 and 61% (approximately 31 million) in 2000. Among the most significant NCDs are diabetes, responsible for about 2.0 million deaths, and cardiovascular diseases, accounting for 17.9 million deaths (World Health Organization, 2021).
The risk of dying from cancer, diabetes, cardiovascular diseases, and chronic respiratory diseases in the South-East Asia region, for those between the ages of 30 and 70, decreased from 23.4% in 2010 to 21.6% in 2019, with a slightly higher decline in both males and females. However, the region is unlikely to meet the 2025 NCDs targets at the current rate of decline. In summary, four main risk factors contribute to NCDs, namely unhealthy diets, physical inactivity, hazardous alcohol use, and tobacco use. Diabetes and hypertension are becoming more common, with an estimated 1,444,528 deaths and 2, 252,981 new cases of cancer in 2020. Moreover, age-standardized incidence and mortality rates are highest for breast and cervical cancers (World Health Organization, 2023).
According to the 2019 Morbidity Survey 2019, approximately 50% of Malaysians were afflicted with at least one NCD, including conditions like hypertension, diabetes, and elevated cholesterol. Malaysia has the highest rate of diabetes prevalence in Southeast Asia, with a sharp rise from 11.2% in 2011 to 18.3% in 2019. In the nation, one in two adults is overweight or obese. According to the National Health and Morbidity Survey 2019, women have the highest prevalence of these problems, at 54.7%, followed by individuals in the 55-59 age range, at 60.9%. Furthermore, 28% of women, 39% of students, and 59% of senior citizens were physically active. However, one in four adults nationwide is physically inactive. The survey also showed low health literacy levels, particularly when encouraging healthy lifestyle choices. For instance, 25.1% of individuals reported physical inactivity, 94.9% reported eating only few fruits and vegetables, and 23.1% reported smoking habits (Institute for Public Health, 2020).
Many types of optimizations have been conducted (Tan et al., 2025; Srisurin et al., 2024; Jusuf et al., 2024; SIripath et al., 2024; Wichapa et al., 2024). Genichi Taguchi developed Mahalanobis-Taguchi System (MTS) for examining multidimensional systems at the end of the 20th century (Taguchi and Jugulum, 2002), as shown in Figure 1. MTS is a pattern recognition technology that leverages data analytics techniques to establish a multivariate measurement scale, enabling quantitative decision-making (Ramlie et al., 2020). One of its key objectives is to classify two groups of samples, such as healthy and unhealthy patients, normal and abnormal conditions, conforming and non-conforming products, or acceptable and non-acceptable approval terms (Ramlie et al., 2021). Furthermore, MTS helps reduce the number of parameters in multivariate analysis, minimizing required data and computational time by identifying the effects of process parameters (Shakya et al., 2012).
MTS has four kinds of methods, which are Taguchi (T), Recognition Taguchi (RT), Mahalanobis Taguchi (MT), and Mahalanobis Taguchi Adjoint (MTA), and the one to choose depends on the system. MTS combines Taguchi’s strong design ideas with Mahalanobis distance, which is used like a measuring scale, to help in system checking and dimension choices (Xiao et al., 2020). It also lets users find how far two people are apart using many variables (Harudin et al., 2021; Abu et al., 2018; Abu et al., 2013; Abu and Jamaludin, 2013). Moreover, MTS is used a lot for recognizing patterns in many systems. It has worked well in places like business control, product checks, health diagnosis, money risk warnings, fault finding, and full evaluations. Mahalanobis distance helps set reference points using samples from reference data, and also builds scales with many dimensions. It also helps with setting class limits (Yao and Lin, 2021).
The main idea behind Mahalanobis distance is when the training data looks like a Gaussian distribution and there is no multicollinearity. When there is damage, the feature vector moves far from the mean of normal data. Even when finding damage location and size is not totally the same as spotting strange patterns, they work kind of the same way. When new damage data fits these conditions, the feature vector stays close to the average vector. However, when the damage type is not the same, it goes farther. When there are just a few samples, getting the covariance becomes hard. Hence, there is a need to get a better way of finding covariance for small data. This helps to find Mahalanobis distances for each group.
Studies have found that using Mahalanobis distance works better with industrial data compared to other methods, showing it is good for detecting drift and useful in real-world applications (Zhao et al., 2021). Empirical results have shown that the method using Mahalanobis distance was better than other few-shot learning techniques and had advantages over traditional and transfer learning methods when working with small samples (Wang et al., 2022). This algorithm is more adaptable and works well for simulations, helping to understand small-sample properties related to Mahalanobis distance (Li et al., 2021). Also, when looking at two datasets, error rates of 6.71% and 16.85% for one, and 6.35% and 20.65% for another, show that the proposed three-way multi-attribute decision-making (MADM) model using Mahalanobis distance is better than other models (Chen and Liu, 2021). Another thing is that combining energy conservation with oversampling or regularization through Mahalanobis distance leads to a stable and reliable method in the long run (Yuan et al., 2021). In addition, it has been shown that Mahalanobis distance can be useful in big data and wireless network technologies, making it helpful for both data analysis and decision-making (Zhang et al., 2021).
Some new studies have looked into how Mahalanobis distance works in different places. Zhao et al. (2021) made a way to find concept drift in factory data without using any labels. They used a segmentation model with Mahalanobis distance. Wang et al. (2022) brought up a method for few-shot damage detection using Mahalanobis distance. This helps find new damage types with just a few labeled samples. Meanwhile, Li et al. (2021) tried simulating data points using Mahalanobis values taken from a whole group, and showed that this kind of method is still not common. Chen and Liu (2021) made a different decision-making model that does not only rank choices, but also states whether a choice is accepted, delayed, or rejected. This method is about how decision-makers actually think. Another study by Yuan et al. (2021) built a method using Mahalanobis distance and added discrete empirical interpolation (DEIM) to lower errors while keeping kinetic energy rules. At the same time, Zhang et al. (2021) came up with a way to choose features using Mahalanobis distance. This helped to reduce the number of features and keep only the ones that matter most for meaning and performance.
MTS makes use of orthogonal arrays (OA) and signal-to-noise ratios to pick the right feature values from the main benchmark data, as shown in Figure 2. This way, the sample stays understandable and the chosen features are easier to test and check (Iquebal et al., 2014). MTS also runs a strong parameter design to see how each parameter works using fewer test cases (Aris et al., 2023; Ihsan Yanikoglu et al., 2022). At the same time, the cost of computing this method (Kamil et al., 2019; Zamrud et al., 2019; Abu et al., 2017) can go down by making classification more accurate and using fewer features that separate the data well (Xue et al., 2019).
The degree of contribution generated by MTS methodology serves as a pattern recognition and optimization algorithm for classification, dimensionality reduction, and diagnosis in multivariate systems. Currently, various machine learning and artificial intelligence techniques, such as random forest, support vector machines, and artificial neural networks, are widely used for classification and feature selection. However, these methods often face challenges related to imbalanced data.
MTS helps to lower the number of features or system dimensions without making identification worse. It does this by using signal-to-noise ratio and orthogonal arrays (OA). The process of choosing features is improved by OA and the signal-to-noise ratio. Mostly, two-level OA is used to find the most important features. In this type, Level 1 means the feature is included, and Level 2 means it is not. Each row in the OA tells which features are used for that experiment. For every experiment, the chosen variables are used to find the Mahalanobis distance from abnormal data, and then the signal-to-noise ratio is calculated as the answer to the combination.
Many studies have investigated the benefits of checking how much each feature contributes using the MTS method. It has been shown that MTS works well for finding patterns in data with many variables and helps figure out causes (Chen et al., 2021). Because MTS can work using fewer important features, it often does better than normal Mahalanobis distance classifiers (Zhang and Liu, 2021). It is also good for checking recovery progress with only a few needed features (Wang et al., 2022). The method has been used to tell apart different pavement conditions too (Li et al., 2022). MTS is a good tool for classification tasks. It checks how abnormal samples are and confirms which variables work best, using OA and signal-to-noise ratios (Tang et al., 2023). Unlike the common machine learning models that need lots of training data, MTS makes a measurement scale using just one class of data. This makes it better at dealing with class imbalance.
A lot of works have investigated how the degree of contribution matters in MTS across many areas. Chen et al. (2021) built an online system that used fuzzy probability to manage uncertainties in chemical processes. The results showed that the method gave better accuracy than others. Zhang and Liu (2021) made a way to check how steady lithium-ion battery packs are using MTS, which helped find and measure changes that happen over time. Wang et al. (2022) made a quick Mahalanobis classification method that mixes symmetrical uncertainty with Mahalanobis kernel PCA. This gave a two-step reduction approach that made accuracy, G-mean, and speed better. Li et al. (2022) used linguistic term sets to go through large comment data and find out which features matter most based on contribution. Their system used a three-way decision method and a better classifier. Tang et al. (2023) also came up with a two-step method using binary particle swarm optimization to improve feature picking and to find a good boundary between healthy and unhealthy parts. This study identified gaps and missing solutions regarding health performance among academicians. The effect of Mahalanobis distance and the degree of contribution on health performance of academicians can be analyzed through multidimensional statistical methods, particularly in areas such as stress levels, workload management, work-life balance, and overall well-being. When applied to health performance of academicians, Mahalanobis distance can identify abnormal health patterns by analyzing variables such as workload, sleep patterns, stress levels, and physical activity. Meanwhile, when applied to academicians, the degree of contribution can determine key stressors such as teaching load, study pressure, administrative duties, and work-life balance. Generally, both Mahalanobis distance and the degree of contribution provide a data-driven method to develop personalized well-being strategies, improve institutional policies for workload and mental health support, as well as foster productivity by ensuring healthier academic environments.
Figure 3 presents the study flow, comprising four main steps that define the methodology used in this study. The first step, problem definition, involved identifying health issues among academic staff at local university. This was followed by the data collection phase, where relevant health data were obtained from the university’s health center.
The data investigation phase entailed systematic analysis of the gathered data using MTS methods to extract meaningful insights. Lastly, the analysis and conclusion phase focused on reviewing results, drawing conclusions, and formulating recommendations. This structured methodology provided a systematic framework, offering valuable guidance for further investigations in this field.
This study involved academicians from 11 academic faculties, including the Faculty of Computing, Faculty of Industrial Management, Faculty of Industrial Sciences and Technology, Faculty of Civil Engineering Technology, Faculty of Electrical and Electronics Engineering Technology, Faculty of Chemical and Process Engineering Technology, Faculty of Mechanical and Automotive Engineering Technology, Faculty of Manufacturing and Mechatronic Engineering Technology, Centre for Modern Languages, Centre for Human Sciences, and Centre for Mathematical Sciences. Furthermore, a total of 17 parameters were examined, including glucose, lipid profile, and blood pressure.
Figure 1 Evolution of Taguchi Method
Figure 2 Orthogonal Array
Figure 3 Study flow of health performance among academicians using MTS
Glucose included random plasma glucose and fasting plasma glucose, while the lipid profile comprised total cholesterol, triglycerides, high-density lipoprotein (HDL), and low-density lipoprotein (LDL). In addition, blood pressure measurements included systolic (untreated), systolic (treated), diastolic, and pulse. These parameters were based on the Clinical Practice Guidelines from experts. Table 1 provides a detailed overview of the parameters used, along with their classifications.
Table 1 Parameter used in the study to measure the abnormalities
Table 1 Parameter used in the study to measure the abnormalities (Cont.)
Table 1 Parameter used in the study to measure the abnormalities (Cont.)
Pattern recognition was emphasized in the RT Method. Items inside and outside the unit space and those outside the unit space were separated into two categories by the RT Method techniques. When multiple unit spaces are available and a measure output's category is obvious, but its true value is unknown, the RT Method can be applied. The average parameter value in normal group unit space is provided in equation (1).
The linear formula, L, and effective divider, r, from Equations (3) and (4) are needed to calculate the sensitivity, for the initial unit space samples in Equation (2).
Total variation, ST element variation proportionate to , error variance, Se, and error variance, Ve are obtained by evaluating Equations (5)-(7) and Equation (8). These results are later substituted into the standard S/N ratio, n.
Equation (9) computes the standard S/N ratio, n. There is a stronger correlation between input and output when the n value is higher.
A scatter diagram is produced by calculating Y1 and Y2. Equations (10) and (11) show the formulas for Y1 and Y2.
The origin is estimated and the averages for Y1 and Y2 are calculated using equations (12) and (13).
The final step involves using Equation (14) in the normal group to calculate Mahalanobis distance.
The same formula was used to calculate both the normal and the abnormal groups. However, the abnormal group should be normalized before doing any computations. It should be noted that the effective, r’, in Equation (4) and the average values, , of the samples and parameters in Equation (1) were comparable to the normal group value.
T Method established significant parameters after RT Method determined normal and abnormal MD. This method produced average output in a uniform unit space. The majority of the samples were normal, while the remaining were not. In the normal group unit space, the parameter and output average values were found using equations (15) and (16).
The abnormal group normalization technique aimed to remove extraneous information from the data to increase the information's flexibility. Equations (17) and (18) compute the normalized input and output data.
To obtain the S/N ratio, n, and proportional coefficient, for each parameter, use the steps found in Equations (19)–(25).
The slope increases to the right when is positive, but decreases when it is negative. A significant correlation between the input and output is shown by positive n values, while negative values signify no correlation.
For each parameter, the proportional coefficient and SN ratio
are used to calculate the integrated estimate value of the abnormal group. Equation (26) is used to calculate the integrated estimate value. Each parameter's normalized values are expressed as x_i1, x_i2, …, x_ik.
Equation (27)-(33) can be used to calculate the estimated S/N ratio, n. Specifically, the suitability of the OA provides the foundation for the predicted S/N ratio, n.
The significance of the parameter was established by the reduction in the estimated SN ratio, n, in the absence of its use. The assessments used OA levels 1 and 2. Under certain conditions, OA measured the predicted S/N ratio, n. When there is a two-level OA, parameter level 1 is used, and level 2 is not. The difference between levels 1 and 2 averages for each parameter in the predicted S/N ratio, n, showed the relative significance of the parameters. When a larger SN ratio, n, is used, the degree of contribution is positive. Otherwise, when it is not used, the degree of contribution parameter is negative.
The RT Method quickly and efficiently performed pattern recognition and classification. Its use of a small-scale database was another key feature. Therefore, it was particularly effective in situations where multiple patterns needed to be recognized, such as character recognition. The method also used Mahalanobis distance values to generate line graphs and scatter diagrams for normal and abnormal data.
Figure 4 presents the scatter diagram of health performance for all academicians in 2022. The values of Y1 and Y2 represent the normal and abnormal data, respectively, subsequently plotted on the scatter diagram. The diagram visually differentiates between the normal and abnormal data using two colors, namely green for normal data and red for abnormal. This study used 17 parameters to achieve the results. Based on analysis, Mahalanobis distance for abnormal data ranged between a minimum of 0.0130 and a maximum of 44.5121. Meanwhile, it ranged between 0.017623 and 18.1934 for normal data. Therefore, the highest distance value recorded was 44.5121. There was some overlap between normal and abnormal data, with 48 samples overlapping. The average distance for 2022 was 5.9839. Abnormal data had a correlation coefficient (r) of -0.3636, while normal data recorded -0.6161. This confirmed a strong negative correlation between normal and abnormal data.
Figure 4 Health performance of academicians 2022
Figure 5 presents a scatter plot showing health performance of academicians in 2023. Based on analysis, Mahalanobis distance for abnormal data ranged from a minimum of 0.012843 to a maximum of 36.9862. For normal data, the distance spanned from 0.0028 to 8.4052. Therefore, the highest value recorded in 2023, as shown in the scatter plot, was 36.986225. There was an overlap between normal and abnormal data, with 122 samples falling within this range. In addition, the average Mahalanobis distance value for 2023 was 3.6131. The correlation coefficient (r) for normal and abnormal data was -0.5921 and -0.6252, respectively, confirming a strong negative correlation.
Table 2 presents the comparison of the data distribution across six selected faculties, categorized by the years 2022 and 2023. In 2023, the Faculty of Industrial Management recorded six abnormal samples. According to the study, Mahalanobis distance values for abnormal samples ranged from a minimum of 0.0128 to a maximum of 13.1484. Meanwhile, the distance for normal samples ranged from 0.0562 to 5.1124. The key contributing parameters to these abnormalities included cholesterol, triglycerides, systolic blood pressure, diastolic blood pressure, depression, stress, and anxiety.
Figure 5 Health performance of academicians 2023
In 2023, the Faculty of Civil Engineering Technology identified ten abnormal samples. Mahalanobis distance for abnormal samples ranged from 0.2079 to 7.4646, while the values for normal samples ranged from 0.1745 to 8.4052. Three samples also showed an overlap between normal and abnormal data. These variations could be attributed to cholesterol, triglycerides, systolic blood pressure, depression, stress, and anxiety. Furthermore, the Faculty of Electrical and Electronics Engineering Technology recorded 17 abnormal samples in 2023. The distance values for abnormal samples ranged from 0.0153 to 42.1261, while the normal samples ranged from 0.0204 to 1.9469. The contributing parameters included blood sugar, cholesterol, triglycerides, systolic blood pressure, depression, stress, and anxiety.
In the Centre for Modern Languages, 30 samples were classified as abnormal in 2023. Mahalanobis distance values for abnormal samples ranged from 0.0302 to 12.5126, while normal samples ranged from 0.0521 to 1.9148. The scatter diagram showed an overlap of 17 samples between normal and abnormal categories. These abnormalities could be attributed to blood sugar, cholesterol, triglycerides, and systolic blood pressure. For the Faculty of Industrial Science and Technology in 2022, 15 samples were identified as abnormal. The distance values for abnormal samples ranged from 0.1097 to 25.0558, while normal samples ranged from 0.0428 to 18.1934. One normal sample had the highest distance of 18.1934, corresponding to Y1 = 0.6409 and Y2 = 21.2808. This case occurred despite most parameters falling within the normal range. The key contributing factors included cholesterol, triglycerides, systolic blood pressure, diastolic blood pressure, and depression.
In 2022, the Faculty of Chemical and Process Engineering Technology identified 28 abnormal samples. The distance values for abnormal samples ranged from 0.0403 to 37.3656, while normal samples ranged from 0.1230 to 1.6096. The scatter diagram presented one sample plotted far from the rest, identified as [0.3269, 21.7305]. This occurred due to the majority of parameters falling within the abnormal range. The contributing factors included cholesterol, triglycerides, systolic blood pressure, diastolic blood pressure, depression, stress, and anxiety.
T Method was specifically applied to a dataset consisting of 197 samples, categorized into two groups, namely the normal group with 48 samples and the abnormal with 149 samples. A total of 17 parameters were used to evaluate the output. Mahalanobis distance value concentration ranged from 0 to 4.2, with 157 samples falling within this range. Among the examined data, sample number 53 showed the lowest distance at 0.0134, while number 57 had the highest at 128.4785. The average distance across all samples was 4.7979, corresponding to sample number 105. Furthermore, four samples had distance values close to the average, namely sample numbers 104 (4.265316), 83 (4.84195), 76 (4.888205), and 146 (4.952923). Signal data normalization was conducted using average values calculated from the unit space samples. To normalize the signal data, the average value of each classification and response variable was subtracted. Table 3 presents the unit space and signal data in descending order. Furthermore, the computation of output M1 for sample number 1 of random plasma glucose X11 is presented as follows.
Table 2 Comparison of data distribution in 2022 and 2023
Table 2 Comparison of data distribution in 2022 and 2023 (Cont.)
X11= 5.8-0 = 5.8
M1= 0.013494- 4.797933= -4.784439
In a statistics-based method, normalization is typically achieved by dividing the residual amount obtained after subtracting the average values by the parameter’s standard deviation. Parameters with a standard deviation of zero in the unit space are significant for estimation and prediction, preventing proper computation.
Table 3 Unit space and signal data
A parameter-by-parameter computation of the proportional coefficients and the signal-to-noise ratio was performed to determine which parameters were useful for prediction and estimation. Figure 6 presents a scatter diagram showing the relationship between each parameter, such as random plasma glucose and fasting plasma glucose, and the output value. The horizontal axis represents the output value, while the vertical axis represents the parameter. The zero point serves as the unit space center for both axes. Using the T-method, the relationship between parameter and output values was analyzed to calculate the proportional coefficients and the S/N ratio. The closer the relationship between the output value and a given parameter to a straight line, the larger the S/N ratio. Parameters with a stronger linear relationship contribute more significantly when estimating the overall output. Moreover, for each parameter, the proportional coefficient quantifies the degree of the line’s inclination.
Based on Figure 6(i), the proportional coefficient was negative, confirming a downward slope. Despite minimal variation, the data points were distributed uniformly along the regression line. This assumption was supported by the large S/N ratio, confirming systolic (not treated) as suitable for estimation. Meanwhile, the lines in Figures 6(j) and 6(k) showed an upward slope to the right, meaning the proportional coefficients were positive. The graph showed the data points were neatly arranged along a regression line intersecting the origin, with minimal scatter. Given the large S/N ratio, systolic (treated) and diastolic measurements were considered well-suited for estimation.
Figure 6 Scatter diagram of output for each parameter (Cont.)
Table 4 presents the proportional coefficients and the signal-to-noise ratio for each parameter. Other parameters also had corresponding values. A larger S/N ratio confirmed a significant contribution of the parameter. When the S/N ratio is negative, it is interpreted as zero. However, in these cases, the parameter will not be used in computing the general estimation value.
Table 4 The proportional coefficients,
Figure 7 is a scatter plot showing the distribution of actual and estimated signal data values. The vertical axis represents the actual values, while the horizontal axis represents the estimated values. The linear pattern of the estimate confirmed a high-quality estimation, as evidenced by the data points clustering near the green line and the relatively strong correlation. This also confirmed a strong relationship between the estimated and actual values in the signal data distribution.
All 17 parameters were used to generate general estimates. However, the integrated estimation used only a subset of the parameters, disregarding the remaining information. To assess the importance of each parameter, an OA was applied. OA helped improve the accuracy of estimation and prediction by analyzing the relationships between parameters. Specifically, the L44 OA was chosen for parameter allocation. The L44 OA, consisting of four prime-type arrays, was selected for its ability to optimize the effects of parameter interactions. Consequently, Level 1 confirmed the parameters used, while Level 2 represented unused parameters. Table 5 serves as an auxiliary reference for the integrated estimation of the S/N ratio. The integrated estimate of the S/N ratio was calculated based on the L44 OA.
Figure 7 Distribution of actual and estimated values of signal data
Based on the integrated estimate of the S/N ratio, a broken-line graph of the S/N ratio was created in Figure 8. The slope, declining from Level 1 to 2, was crucial for output prediction. When Level 1 is subtracted from Level 2, a descending slope occurs, resulting in a positive distribution degree.
Table 5 Integrated estimate S/N ratio for each parameter
Figure 8 Ratio broken graph 2022
Conversely, when Levels 1 and 2 are subtracted and produce insignificant parameters, a negative degree of contribution is observed. In this line graph, seven parameters showed an ascending trend (negative degree of contribution), including parameters 1, 5, 6, 10, 12, 15, and 17. Meanwhile, ten parameters showed a descending trend (positive degree of contribution), including parameters 2, 3, 4, 7, 8, 9, 11, 13, 14, and 16. Specifically, parameter 9 (Diastolic) showed a descending slope, as the subtraction between Level 1 (24.0915) and Level 2 (-23.5384) resulted in a negative degree of contribution of -0.553142892.
In conclusion, this study showed the number of academicians increased from 197 in 2022 to 370 in 2023, confirming a growing awareness of health among the workforce. In 2022, 24.37% of employees were considered healthy, while 76% were not. By 2023, the proportion of healthy employees increased by 33%, leaving 67% still classified as unwell. These health trends could be attributed to various factors, including diet, lifestyle, and sugar consumption. Furthermore, MTS had a significant impact on health performance of academicians by providing a systematic method for diagnosing and monitoring health conditions. By using multivariate analysis, MTS helped identify patterns and deviations in health metrics, enabling the early detection of potential health issues. This predictive capability allowed for targeted interventions, improved decision-making, and personalized health strategies. Consequently, MTS contributed to improving overall well-being, reducing health risks, and promoting a healthier lifestyle among academicians.
The authors are grateful to Universiti Malaysia Pahang Al-Sultan Abdullah for funding this study under the grant code PGRS230319.
Author Contributions
Conceptualization, Ahmad Shahrizan Abdul Ghani; Writing–original draft, Nur Aisyah Mardhiah Halim; Writing–review &editing, Nurul Haziyani Aris; Supervision, Mohd Yazid Abu; Funding acquisition, Nur Najmiyah Jaafar. All authors have read and agreed to the published version of the manuscript.
Conflict of Interest
The authors declare no conflict of interest.
Abu, MY & Jamaludin, KR 2013, ‘Application of Mahalanobis-Taguchi system on crankshaft as remanufacturing automotive part: a case study’, Advanced Materials Research, vol. 845, pp. 883–888, https://doi.org/10.4028/www.scientific.net/amr.845.883
Abu, MY, Jamaludin, KR & Ramlie, F 2013, ‘Pattern recognition using Mahalanobis-Taguchi system on connecting rod through remanufacturing process: A case study’, Advanced Materials Research, vol. 845, pp. 584–589, https://doi.org/10.4028/www.scientific.net/amr.845.584
Abu, MY, Jamaludin, KR & Zakaria, MA 2017, ‘Characterisation of activity based costing on remanufacturing crankshaft’, International Journal of Automotive and Mechanical Engineering, vol. 14, no. 2, pp. 4211–4224, https://doi.org/10.15282/ijame.14.2.2017.8.0337
Abu, MY, Norizan, NS & Rahman, A 2018, ‘Integration of Mahalanobis-Taguchi system and traditional cost accounting for remanufacturing crankshaft’, IOP Conference Series Materials Science and Engineering, vol. 342, pp. 012005–012005, https://doi.org/10.1088/1757-899x/342/1/012005
Aris, NHA, Abu, MY, Zaini, SNAM, Jamil, MAM, Pinueh, NS, Muhammad WZAW, Ramlie, F, Harudin, N & Emelia, S 2023, ‘Mahalanobis-Taguchi system and time-driven activity-based costing integration of printed circuit board’, Journal of Theoretical and Applied Information Technology, vol. 101, pp. 8247–8261.
Chen, H & Liu, J 2021, ‘A three-way multi-attribute decision-making model based on Mahalanobis Distance’, Decision Support Systems, vol. 145, p. 113521, https://doi.org/10.1016/j.dss.2021.113521
Chen, H, Zhang, P & Liu, J 2021, ‘A probabilistic fuzzy evaluation system for uncertainty management in chemical processes based on degree of contribution through MTS’, Chemical Engineering Journal, vol. 420, p. 129876, https://doi.org/10.1016/j.cej.2021.129876
Harudin, N, Ramlie, F, Muhamad, WZAW, Muhtazaruddin, MN, Jamaludin, KR, Abu, MY & Marlan, ZM 2021, ‘Binary bitwise artificial bee colony as feature selection optimization approach within Taguchi’s T-method’, Mathematical Problems in Engineering, 2021, pp. 1–10, https://doi.org/10.1155/2021/5592132
Ihsan Yanikoglu, Erinç Albey, & Serkan Okçuoglu 2022, ‘Robust parameter design and optimization for quality engineering’, Operations Research Forum, vol. 3, no. 1, https://doi.org/10.1007/s43069-022-00121-3
Institute for Public Health 2020, National Health and Morbidity Survey (NHMS) 2019: Non-communicable diseases, healthcare demand, and health literacy—Key findings, Ministry of Health Malaysia, pp. 1-40, https://iptk.moh.gov.my/images/technical_report/2020/
Iquebal, AS, Pal, A, Ceglarek, D & Tiwari, MK 2014, ‘Enhancement of Mahalanobis–Taguchi system via rough sets based feature selection’, Expert Systems with Applications, vol. 41, no. 17, pp. 8003–8015, https://doi.org/10.1016/j.eswa.2014.06.019
Jusuf, A, Jarwadi, MH, Hastungkorojati, DG, Gunawan, L, Akbar, M, Zakaria, K, Izzaturrahman, MF & Palar, PS 2024, ‘Design exploration and optimization of a multi-corner crash box under axial loading via gaussian process regression’, International Journal of Technology, vol. 15, no. 6, pp. 1749-1770, https://doi.org/10.14716/ijtech.v15i6.7278
Kamil, NNNM, Abu, MY, Zamrud, NF & Safeiee, FLM 2019, ‘Analysis of magnetic component manufacturing cost through the application of time-driven activity-based costing’, Lecture Notes in Mechanical Engineering, pp. 74–80, https://doi.org/10.1007/978-981-15-0950-6_12
Li, X, Zhang, Y & Zhao, Q 2021, ‘Simulation studies on small-sample properties using mahalanobis distance’, Journal of Computational Statistics, vol. 39, no. 2, pp. 223-239, https://doi.org/10.1007/s00180-021-01104-5
Li, X, Zhao, Q & Wang, L 2022, ‘Classification of pavement conditions using mahalanobis-taguchi system and degree of contribution analysis’, Journal of Infrastructure Systems, vol. 28, no. 3, p. 04022030, https://doi.org/10.1061/(ASCE)IS.1943-555X.0000709
Ramlie, F, Muhamad, WZAW, Harudin, N, Abu, MY, Yahaya, H, Jamaludin, KR & Talib, HHA 2021, ‘Classification performance of thresholding methods in the Mahalanobis–Taguchi system’, Applied Sciences, vol. 11, no. 9, pp. 3906–3906, https://doi.org/10.3390/app11093906
Ramlie, F, Muhamad, WZAW, Jamaludin, KR, Cudney, E & Dollah, R 2020, ‘A significant feature selection in the mahalanobis taguchi system using modified-bees algorithm, International Journal of Engineering Research and Technology, vol. 13, no. 1, p. 117, https://doi.org/10.37624/ijert/13.1.2020.117-136
Shakya, YB, Guruge, S, Hynie, M, Akbari, A, Malik, M, Htoo, S & Alley, S 2012, ‘Aspirations for higher education among newcomer refugee youth in Toronto: Expectations, challenges, and strategies’, Refuge: Canada's Journal on Refugees, vol. 27, no. 2, pp. 65–78, https://doi.org/10.25071/1920-7336.34723
SIripath, N, Jantepa, N, Sucharitpwatskul, S, Suranuntchai, S, 2024, ‘Integrating taguchi method and finite element modelling for precision ball joint manufacturing with AISI 1045 medium carbon steel’, International Journal of Technology, vol. 15, no. 6, pp. 1801-1822, https://doi.org/10.14716/ijtech.v15i6.7132
Srisurin, P, Guerra, A, Jarumaneeroj, P 2024, ‘Traffic simulation models to enhance signal timing in an oversaturated network: a comparative study of optimizing individual intersections versus the entire network. International Journal of Technology, vol. 15, no. 6, pp. 1678-1696, https://doi.org/10.14716/ijtech.v15i6.7123
Taguchi, G & Rajesh Jugulum 2002, ‘The mahalanobis–taguchi strategy’, https://doi.org/10.1002/9780470172247
Tan, YH, Chai, MK, Wong, LS, Ong, MY & Rajamani, R 2025, 'Optimizing microwave-assisted extraction of carbohydrate from scenedesmus sp. cultivated in domestic wastewater', International Journal of Technology, vol. 16, no. 1, pp. 255-274, https://doi.org/10.14716/ijtech.v16i1.7301
Tang, W, Sun, H & Guo, R 2023, ‘Optimized feature selection in binary particle swarm classification via mahalanobis-taguchi system’, Expert Systems with Applications, vol. 213, p. 118902, https://doi.org/10.1016/j.eswa.2023.118902
Wang, Y, He, L & Sun, J 2022, ‘Fast mahalanobis classification using symmetrical uncertainty and mahalanobis kernel PCA’, Pattern Recognition, vol. 127, p. 108637, https://doi.org/10.1016/j.patcog.2022.108637
Wang, Y, He, L & Sun, J 2022, ‘Few-shot damage detection using mahalanobis distance for limited labeled samples’, Structural Health Monitoring, vol. 21, no. 4, pp. 987-1003, https://doi.org/10.1177/14759217221083148
Wichapa, N, Pawaree , N, Nasawat, P, Chourwong, P, Sriburum, A, Khanthirat, W 2024, ‘Process of solving multi-response optimization problems using a novel data envelopment analysis variant-taguchi method. International Journal of Technology, vol. 15, no. 6, pp. 2038-2059, https://doi.org/10.14716/ijtech.v15i6.7134
World Health Organization 2021, Noncommunicable diseases, Retrieved from https://www.who.int/news-room/fact-sheets/detail/noncommunicable-diseases
World Health Organization 2023, Noncommunicable diseases are the no. 1 killers in the WHO South-East Asia Region, World Health Organization, Retrieved from https://www.who.int/southeastasia/activities/noncommunicable-diseases-are-the-no.-1-killers-in-the-who-sear
Xiao, L, Zhang, Y & Wang, J 2020, ‘Optimized mahalanobis–taguchi system for high-dimensional small sample data classification’, Complexity, 2020, p. 4609423, https://doi.org/10.1155/2020/4609423
Xue, Y, Xue, B & Zhang, M 2019, ‘Self-adaptive particle swarm optimization for large-scale feature selection in classification. acm transactions on knowledge discovery from data, vol. 13, no. 5, pp. 1–27, https://doi.org/10.1145/3340848
Yao, L & Lin, T-B 2021, ‘Evolutionary mahalanobis distance-based oversampling for multi-class imbalanced data classification’, Sensors, vol. 21, no. 19, p. 6616, https://doi.org/10.3390/s21196616
Yuan, B, Tang, W & Guo, S 2021, ‘Energy conservation and regularization using mahalanobis distance for long-term stability’, Applied Mathematics and Computation, vol. 398, p. 125715, https://doi.org/10.1016/j.amc.2021.125715
Zamrud, NF, Abu, MY, Nik Mohd Kamil, NN & Safeiee, FLM 2019, ‘The impact of capacity cost rate and time equation of time-driven activity-based costing (tdabc) on electric component’, Lecture Notes in Mechanical Engineering, pp. 81–87, https://doi.org/10.1007/978-981-15-0950-6_13
Zhang, K & Liu, W 2021, ‘Consistency evaluation of lithium-ion battery packs using mahalanobis-taguchi system and degree of contribution analysis’, Journal of Energy Storage, vol. 42, p. 103043, https://doi.org/10.1016/j.est.2021.103043
Zhang, K, Xu, M & Li, W 2021, ‘Feature selection and dimensionality reduction via mahalanobis distance. Big Data Research, vol. 24, p. 100182, https://doi.org/10.1016/j.bdr.2021.100182
Zhao, P, Chen, X & Li, H 2021, ‘Concept drift detection in industrial data using mahalanobis distance segmentation’, Expert Systems with Applications, vol. 178, p. 115003, https://doi.org/10.1016/j.eswa.2021.115003
