Risk Modeling in the Oil and Gas Industry
Corresponding email: darya.kryz@yandex.ru
Published at : 29 Dec 2023
Volume : IJtech
Vol 14, No 8 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i8.6852
Rodionov, D., Gataullin, M., Smirnova, I., Konnikov, E., Kryzhko, D., Shmatko, A., 2023. Risk Modeling in the Oil and Gas Industry. International Journal of Technology. Volume 14(8), pp. 1663-1674
| Dmitriy Rodionov | Peter the Great St.Petersburg Polytechnic University, Russia, St.Petersburg, Polytechnicheskaya 29, 195251, Russian Federation |
| Marcel Gataullin | Ufa State Petroleum Technological University, Ufa, Republic of Bashkortostan. Ufa. Kosmonavtov st., 1450064, Russian Federation |
| Irina Smirnova | Peter the Great St.Petersburg Polytechnic University, Russia, St.Petersburg, Polytechnicheskaya 29, 195251, Russian Federation |
| Evgenii Konnikov | Peter the Great St.Petersburg Polytechnic University, Russia, St.Petersburg, Polytechnicheskaya 29, 195251, Russian Federation |
| Darya Kryzhko | Peter the Great St.Petersburg Polytechnic University, Russia, St.Petersburg, Polytechnicheskaya 29, 195251, Russian Federation |
| Alexey Shmatko | Institute for Regional Economic Studies, Russian Academy of Sciences, St. Petersburg, Russian Federation |
The oil and gas industry is a
sector that is prone to risks that can have severe consequences for both the
environment and the economy. In this study. the aim is to develop an effective
mathematical tool for risk modeling in the oil and gas industry. The research
proposes a simulation modeling approach that focuses on two key risk parameters
- frequency and severity. By using differentiated distributions. the unique
properties of risk in the oil and gas industry can be effectively described,
and an algorithm can be developed for practical applications. The findings of
this study have significant implications for the oil and gas industry,
policymakers, and investors. By using an effective mathematical tool for risk
modeling. they can identify and manage risks more effectively, reduce the
likelihood of accidents and other events that can have severe consequences. and
minimize the potential impact of these events. Overall, this research provides
valuable insights into the development of an effective mathematical tool for
risk modeling in the oil and gas industry. By using simulation modeling and
differentiated distributions. this study proposes an algorithm that can be
practically applied to manage risks effectively in this important sector.
Environment; Investors; Oil and Gas Industry; Risk Modeling
The
oil and gas industry serves as the backbone of the GDP for many nations playing
an integral role in numerous mass production chains. As one of the largest
industries in terms of dollar value it not only contributes substantially to
economic output but also generates hundreds of thousands of jobs worldwide (Piya et al., 2020). A sudden breakdown in
any of the three global sectors of the oil and gas industry (extraction, transfer,
processing) has serious consequences directly disrupting the rhythm of the supply
chain and creating the potential for an exponential increase in primary
financial losses (Biezma et al., 2020). In addition the oil and
gas industry has an increased level of danger - the most fatal accidents in the
history of oil and gas pipelines have resulted in the death of more than 4.000
people (Biezma et al., 2020). Accordingly, there is a
need to create mechanisms for managing oil and gas industry objects in terms of
preventing the development of emergency situations which requires the formation
of tools for predicting the predisposition of a particular object to the
initiation of a breakdown-risk exposure (Yang, Haugen, and Paltrinieri, 2018).
Risks
are a parameter category indicative of the internal environment of the oil and
gas enterprise. Despite the production specificities of the oil and gas
industry certain limitations apply to predictive mathematical models: it has a
low-risk frequency (accidents happen at a low rate) and at the same time, a
high level of financial losses (Olanipekun and
Alola, 2020). Therefore, a comprehensive examination of
the factors influencing the formation and dynamic activation of risks in the
oil and gas industry should serve as the foundation for devising a mathematical
mechanism to assess an object's risk exposure. This study is
conceptually different from the previous ones in terms of the goal of
developing a risk modeling toolkit that provides analytical capabilities in
conditions of fundamental information constraints, which is typical for the oil
and gas industry. It is precisely the development of a risk modeling toolkit
with the corresponding properties that determine the scientific contribution of
this research. It is necessary to clarify that the developed risk modeling
toolkit is primarily specified in relation to the technical risks of the oil
and gas industry, such as explosions and the release of hazardous substances.
To Before
selecting an instrument for modeling risk parameters it is necessary to
determine its properties in the context of the oil and gas industry. The
specifics of the frequency and severity of risk in the oil and gas industry can
vary depending on many factors such as the field the technologies used on the
field the climatic conditions, the economic and political stability of the
region, etc. Analysis of the Rostekhnadzor (The Federal Service for Ecological,
Technological and Atomic Supervision; Russian Federation) statistics (Gosnadzor, 2023) the total number
of risk events in the industry (for Russia) in 2021 and 2022 is 36 with a total
number of enterprises at 285. Thus, the frequency per enterprise is 3.16%. At
the same time, the average severity is 149 342 767 rubles. Thus, it can be
concluded that the oil and gas industry is low-frequency in terms of risk and
significant in terms of the cost of damage (Olanipekun and
Alola, 2020).
This specificity produces the problem of insufficient statistical arrays for
the training of statistical models with sufficient predictive accuracy. Thus,
the most appropriate is the use of imitation modeling, which will allow us to
model the current conditions of functioning of the industry's enterprises and
thus estimate the most likely values of the considered risk parameters (Rodionov et al., 2022).
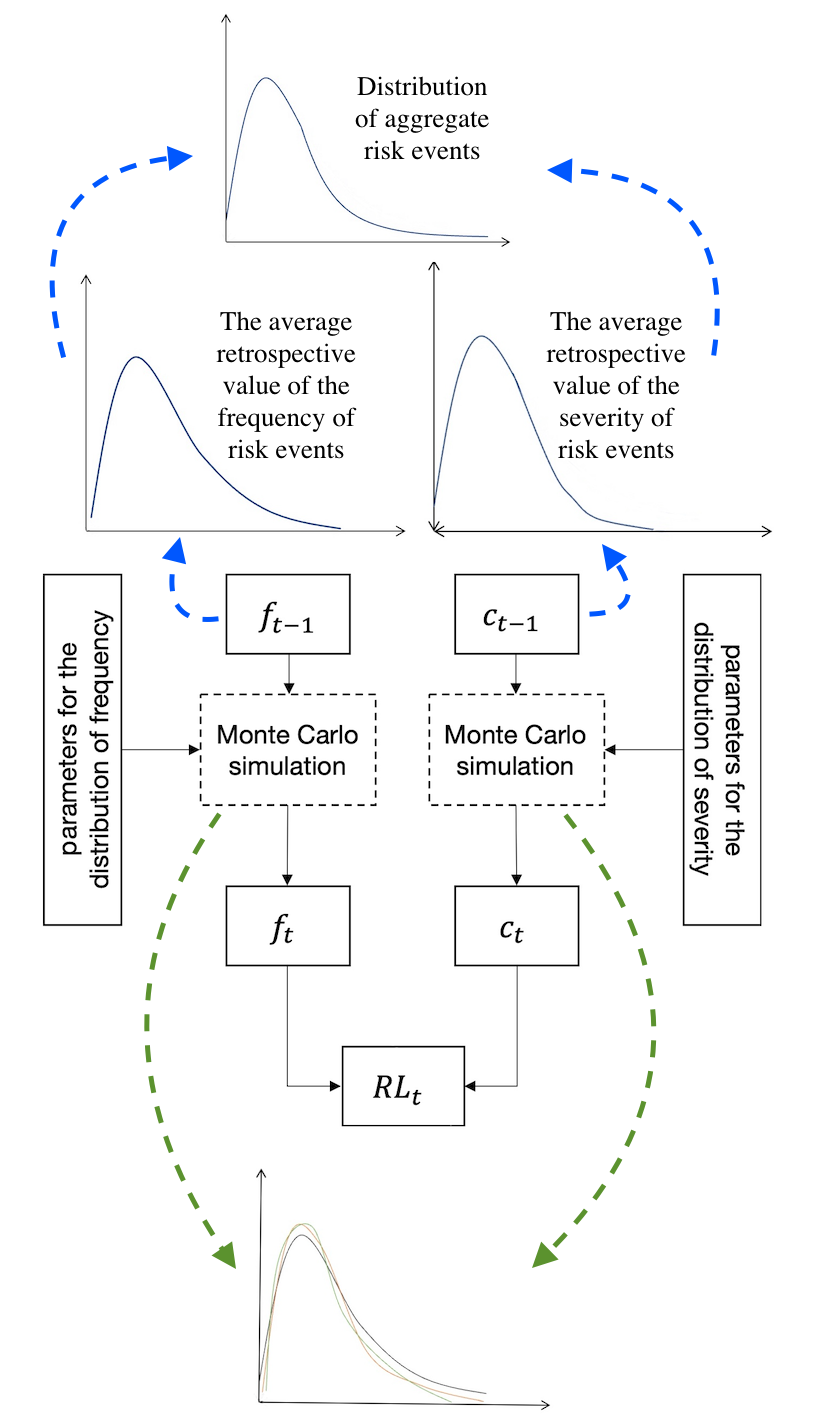
For these purposes Monte Carlo simulation can be used.
Monte
Carlo simulation is a statistical method that is used for modeling random
processes and making decisions based on probabilistic calculations (Hartoyo et al., 2023; Tran, Robbe, and Lim, 2023; Clare, Piggott, and Cotter, 2022). It is based on the idea of generating random numbers
that are then used to create a set of possible scenarios. Monte Carlo
simulation has several drawbacks,
the key of which is the sensitivity to the choice of the random number
generator and the model parameters. Thus, the accuracy of the simulation
results is determined by the quality of selecting the probability distribution
parameters for the frequency and severity of the risk event. Thus,
the algorithm requires aggregation of the historical array describing the
frequency and severity of risk events in the oil and gas industry,
determination of the parameters of frequency and severity of risk events
distribution, generation of the set of component parameters, statistical
generalization of the obtained results and calculation of the integral level of
risk indicator. The described algorithm is presented in Figure 1.
There
are a multitude of statistical distributions that can be used for risk
parameter modeling. The choice of the distribution depends on the assumptions
that can be made about the characteristics of the data. It is necessary to
systematically consider a number of the most commonly used distributions for
such tasks. There are several distributions that have unique advantages for the
purposes of risk event severity modeling specific to the oil and gas industry:
1.
The Gamma Distribution provides the possibility of fine-tuning the shape and
scale, allowing the results of modeling to be adapted to the conditions of
factual reality. Additionally, the Gamma Distribution is a “memoryless”
distribution, which is extremely important for the oil and gas industry due to
the low frequency of risk.
2.
The Pareto Distribution provides the possibility of modeling “heavy tails”,
which is also extremely important for the oil and gas industry due to the high
weight of risk events caused by both technological specialties and the presence
of post-event risks.
3. The Exponential Distribution, like the Gamma Distribution, is “memoryless”, which is extremely important for the oil and gas industry.
Figure 1
Algorithm for assessment of integral risk level indicator, based on Monte Carlo
simulation
Modeling
the severity of a risk event within the context of three distributions in
combination with subsequent comparison of results will significantly increase
the predictive accuracy of the modeling results.
The
nature of risk frequency presents an ambiguous character. While aligning with
the Central Limit Theorem suggests the relevance of utilizing the Normal
Distribution, it is essential to consider potential chain reactions arising
from the inherent risks in the oil and gas industry. This characteristic, often
termed risk accumulation, underscores the need for a nuanced approach to
modeling in this sector. The nature of risk accumulation implies an increased
probability of consecutive risk events, as well as the reverse. Therefore, in
the event of a risk occurrence within a simulation. the probability of
subsequent risk events increases (Ting, Zakariah, and Yusri, 2022).
The parameter that characterizes the strength of this dependence can be
conditionally referred to as internal correlation. In this transformation, it
is reasonable to move from a normal distribution to a multivariate normal
distribution. The probability density function of the multivariate normal
distribution has the following form:
For risk modeling using the multivariate normal distribution, the parameters of the distribution need to be estimated: the vector of means and the covariance matrix. While the vector of means can be determined based on factual data, the covariance matrix requires a subjective-expert approach. The covariance matrix is a matrix containing the pairwise covariances between all the random variables. To construct the covariance matrix, one needs to assess the covariances between all the pairs of variables and then combine them into a matrix. The covariance matrix must be symmetric and positive definite. However, in this case, the simulation process takes on a one-dimensional character. Consequently, the covariance matrix is semantically defined by only one value, represented earlier by the coefficient of internal correlation (corrt). This coefficient ranges from 0 to 1, signifying the degree of risk accumulation. A value of 0 indicates the absence of risk accumulation (implying a normal distribution), while a value of 1 denotes absolute risk accumulation. An example of the product of a risk frequency matrix built on the basis of a multivariate normal distribution and a risk severity matrix built on the basis of the gamma distribution for various values of the risk accumulation coefficient is shown in Figure 2.
Figure 2
The variations of the risk frequency matrix constructed on the basis of the
multivariate normal distribution and the risk severity matrix constructed on
the basis of the Gamma distribution for different values of the risk
accumulation coefficient.
In
order for modeling purposes. the following parameters should become the input
array:
1.
The average retrospective value of the frequency of risk events (ft-1). This
value can be determined on the basis of an existing statistical base and, if
necessary, can be expertly corrected.
2.
The average retrospective value of the severity of risk events (ct-1). The
nature of this parameter is identical to the nature of the previous one.
3.
The internal correlation coefficient (corrt). It is determined by
the expert and can be universalized at the industry level.
4. The shape parameter of the Gamma distribution (k). This parameter reflects the shift of the Gamma function. The scale parameter, in turn, is modeled on the basis of the severity of the risk event:
5. The shape parameter of the Pareto distribution (a) also reflects the shift in the function, like the shape parameter of the Gamma distribution. The minimum value that the random variable can accept is also determined by the severity of the risk event:
6.
The number of risk events over the previous period (n) is determined based on
actual data.
7.
The maximum severity of a risk event (max-cit-1) is also determined based on
actual data but may be subject to expert correction.
Hence, a critical aspect in the discussion revolves around establishing the modeling quality by accurately determining distribution parameters. This challenge is often addressed experimentally, comparing the target indicator derived from actual data with the modeled counterpart. Such an indicator could be the planned loss rate:
Where:
the security fund for compensating for the
consequences of the risk event (in rubles).
As a security fund, the value of the net profit of the enterprise can be used and adjusted by a coefficient of growth. The quality of the modeling will in turn be determined by the closeness of the modeled value to the planned one. For selecting the optimal distribution parameters for modeling. statistical methods such as histograms and distribution graphs can be employed to identify the distribution that best fits the data. The most appropriate technique for this is the use of a cyclical algorithm, which examines combinations of distribution parameters and determines the effective magnitude of those leading to the desired modeled loss. The resulting object of analysis is the shape of the distribution itself. The shape of the probability distribution can tell a lot about the risks associated with a given event or phenomenon. For example, if the distribution is skewed to the right, it could indicate that risk is elevated and that unaccounted-for factors may increase the likelihood of an unfavorable outcome. If the distribution is symmetrical. it could indicate a uniform distribution of risks. Thus, the internal environmental state of the oil and gas enterprises can be determined by the collective of tested risk distribution characteristics and indicators describing loss, based on the solution of the following simulation problem (see equations 1-3):
Defining the shape parameter is determined by the following objective setting (see equation 7):
The
range of the Gamma distribution shape parameter – [0.1. 9.0]
The
range of the Pareto distribution shape parameter – [1.0. 10.0]
However,
the distribution itself cannot provide complete information about the risk, so
it should be considered in conjunction with a set of indicative parameters,
such as the probability quantiles and probability of exceeding the planned loss
values (see equation 8):
The
developed toolkit requires automation and verification for use in petroleum and
gas industry enterprises. Step by step, the developed methodology can be described by
the following algorithm: 1. Identification of risk portfolio categories. 2.
Assessment of parameters of frequency and severity of categorically specified
risk events based on past experience. 3. Monte Carlo generation of arrays
describing the distribution of frequency and severity of risk events using the
gamma distribution, Pareto distribution, exponential distribution, and
multivariate normal distribution. 4. Evaluation of the distribution properties
using the formed set of indicators.
The
system of modeling tools for indicators of the internal environment state of
oil and gas industry enterprises developed implies using an array of empirical
data which can be obtained both based on an analysis of specific enterprise
activities as well as from official aggregate statistical sources. In the
Russian Federation, control and accounting of risks of oil and gas industry
enterprises is a function of the Federal Service for Ecological. Technological
and Atomic Supervision (Rostekhnadzor), particularly of the department
responsible for oversight of oil-and-gas extraction and chemical production
objects.
According
to the information provided on the department website (Gosnadzor, 2023), risk events are divided into four key groups: 1.
Release of hazardous substances (36%); 2. Uncontrolled explosion (14%); 3.
Destruction of structures (28%); 4. Destruction of equipment (22%).
As
can be seen, the distribution of shares is quite uniform, indicating a systemic
quality of control and supervision. The highest share is held by releases of
hazardous substances, which is primarily due to the fact that this type of
situational risk is a consequence of the realization of local resource risks
(micro-level risks). The smallest share is held by uncontrolled explosions,
which again indicates the systemic quality of control and supervision, leading
to the possibility of preventing such risk events. A significant variance of
shares is observed in the cost aspect (cost of damage or severity of risk
events).
The destruction of structures stands
out as the most significant in terms of the severity of risk event
implementation. This aligns with formal-economic logic, as the destruction of a
structure entails not only the efforts involved in its restoration but also
encompasses the restoration of technical infrastructure, affected assets, and
the processes of dismantling and disposal (Ryan and Bristow, 2023). In this rating, the second is the release of
hazardous substances. This fact is determined by the previously stated thesis
regarding the significance of post-event risks, to which environmental risks
are primarily applicable, which are in turn modeled by the emission of
hazardous substances. An uncontrolled explosion, in turn, is the least
significant in terms of the severity of the risk event, which indicates a high
level of technical safety that minimizes chain reactions (Pishchalkina, Pishchalkin. and Suloeva, 2022).
The
consolidated reports presented by Rostechnadzor allowed to compile a
consolidated risk-statistics table (Table 1).
Before
analyzing the corresponding statistical array, it is necessary to note a number
of technical aspects:
When
aggregating, only data detailed in terms of cost and risk subject (enterprises)
were taken into account. In this regard, the list of risk events participating
in the analysis is less than actual (36 risk events instead of 51 risk events).
Table
1 Consolidated Risk-Statistics of Oil and Gas Industry
2021–2022
|
N |
Type of accident |
Number of accidents |
The average cost of damage |
Damage limit |
Frequency |
Average profit of
the previous period |
|
1 |
Release of hazardous substances |
13 |
126,219,152 |
1,210,000,000 |
4.56% |
16,413,470,244 |
|
2 |
Uncontrolled explosion |
5 |
49,029,453 |
131,011,761 |
1.75% |
21,832,052,400 |
|
3 |
Destruction of structures |
10 |
316,559,663 |
1,239,000,000 |
3.51% |
672,989,600 |
|
4 |
Destruction of equipment |
8 |
105,562,799 |
445,800,000 |
2.81% |
22,954,384,625 |
The average profit
of the previous period was obtained in accordance with the accounting data.
The
frequency of a risk event was obtained per 1 enterprise. According to the data
of the Ministry of Energy of the Russian Federation as of January 1, 2021, oil
and gas condensate production on the territory of the Russian Federation was
carried out by 285 organizations with the right to use subsoil.
The
data aspects limit the objectivity of the conclusions that can be formulated
based on the analysis. However, this restriction is insignificant in the
context of comprehensive risk distribution analysis implied by the formed
instrumentarium.
The
formation of the instrumentarium was performed using the high-level programming
language Python and a complex set of tools libraries, namely the Scipy library,
that enables the generation of arrays of random numbers in accordance with
assigned distributions. Before the risk modeling process is implemented, it is
necessary to determine the level of internal correlation (corrt) (Paltrinieri, Louise, and Genserik, 2019).
As noted earlier, this parameter is expert-driven in terms of definition. For
the purpose of the current research, its value was determined based on the
graph logic. According to this logic, the implementation of separate risk
events on the technological level may lead to the implementation of subsequent
ones, which in turn can be described as a chain reaction. The distribution of
the internal correlation indicator in accordance with key risk groups is
provided in Figure 3.
Figure 3 Distribution of Internal Correlation
Indicators According to Key Risk Groups
The internal correlation indicator largely determines the distribution of frequency of highly weighty risk events. This specificity was reflected in the Gamma and Pareto distributions (Figure 4).
Figure
4 Gamma and Pareto Distribution Parameters
Based on the
presented graph. it can be inferred that the most skewed distributions are
associated with uncontrolled explosions and the destruction of structures,
suggesting a relatively low probability of organizing these risk groups. On the
contrary, the Pareto distribution displays an extremely opposite specificity,
which is largely determined by the weightiness of the risks implied by the
release of hazardous substances. Consequently, the risks of uncontrolled
explosion and destruction of structures are most controllable, whereas the
risks of release of hazardous substances are least controllable. This statement
correlates with the previously made empirical conclusions. The consolidated
results of the modeling of condition indicators within the oil and gas industry.
according to the major risk groups, are presented in Table 2.
As
can be seen, the planned loss for the destruction of structures group is
several times higher than for other groups of risk. This fact is also related
to the already described specificity. However, it differs from the specificity
demonstrated by the modeled parameters of distributions. Therefore, despite the
effectiveness of control, the implementation of risk events of the destruction
of structures group brings losses that are incomparable to the profit of the
enterprise. Consequently, measures to control resource risks should be directed
primarily towards the prevention of such types of risk events. The described
specificity is confirmed by the distribution of modeled losses. The quality of
imitation modeling is principally demonstrated by the minimal deviation of
modeled values of losses compared to the planned ones.
The
maximum deviation is observed when using an exponential distribution, which
confirms the hypothesis about the significance of parameter tuning for the form
of the distribution. Much more detailed conclusions can be drawn from the
analysis of the loss quantiles. The destruction of structures group remains the
most significant in terms of potential damage. In 95% of cases, the damage from
its implementation will be more than 90% of the profit, and in 99% of cases -
more than 170% of the profit. The other risk groups are insignificant in
comparison with it. However, it is worth noting the quantiles of the release of
hazardous substances group, according to which the limit of damage can be about
4%. This specificity indicates that the destruction of structures is most
likely a consequence of a systemic problem,which is realized primarily in
enterprises with a low level of financial security. Thus, the risk specificity
of financially stable enterprises is concentrated within the framework of the
release of hazardous substances risk management.
According
to the provided results, it can be concluded that the probabilities of
exceeding the planned loss are extremely comparable, which in turn indicates a
significant shift in the shape of the distributions. The most significant
values of these indicators are reached for the release of hazardous substances
group. Moreover, the variance of these parameters in terms of distributions is
much higher, specifically in the case of the release of hazardous substances
risks. This fact indicates a high variance of the risk nature and, consequently,
a need for additional research on this risk group. At the same time, the
uncontrolled explosion risks are much more stable and more predictable.
Table
2 Consolidated Results of the Modeling of Condition
Indicators within the Oil and Gas Industry according to the Major Risk Groups
|
Index |
Release of hazardous substances |
Uncontrolled explosion |
Destruction of structures |
Destruction of equipment | |
|
1 |
The planned loss indicator |
0.456% |
0.020% |
16.504% |
0.103% |
|
2 |
Modeled loss
Gamma |
0.456% |
0.020% |
16.497% |
0.103% |
|
3 |
Modeled loss
Pareto |
0.457% |
0.019% |
16.508% |
0.103% |
|
4 |
Modeled loss Exponential |
0.457% |
0.018% |
16.214% |
0.101% |
|
5 |
95th
quantile of Gamma loss |
2.032% |
0.183% |
93.894% |
0.748% |
|
6 |
95th
quantile of Pareto loss |
1.655% |
0.182% |
91.563% |
0.671% |
|
7 |
95th
quantile of Exponential loss |
2.328% |
0.084% |
108.815% |
0.746% |
|
8 |
99th
quantile of Gamma loss |
3.241% |
0.446% |
173.027% |
1.734% |
|
9 |
99th
quantile of Pareto loss |
2.707% |
0.438% |
171.751% |
1.613% |
|
10 |
99th
quantile of Exponential loss |
4.038% |
0.561% |
208.727% |
1.942% |
|
11 |
The probability
of exceeding the planned values for Gamma |
0.000% |
0.000% |
4.391% |
0.000% |
|
12 |
The probability
of exceeding the planned values for Pareto |
0.000% |
0.000% |
3.732% |
0.000% |
|
13 |
The probability
of exceeding the planned values for Exponential |
0.000% |
0.000% |
5.665% |
0.000% |
|
14 |
The probability
of exceeding the planned values by 5% for Gamma |
32.401% |
6.649% |
23.282% |
13.512% |
|
15 |
The probability
of exceeding the planned values by 5% for Pareto |
41.366% |
6.649% |
23.405% |
13.802% |
|
16 |
The probability
of exceeding the planned values by 5% for Exponential |
27.014% |
6.193% |
18.243% |
11.850% |
|
17 |
The probability
of exceeding the planned values by 10% for Gamma |
31.713% |
6.649% |
23.245% |
13.475% |
|
18 |
The probability
of exceeding the planned values by 10% for Pareto |
41.366% |
6.649% |
23.405% |
13.802% |
|
19 |
The probability
of exceeding the planned values by 10% for Exponential |
26.478% |
6.172% |
18.033% |
11.766% |
|
20 |
The probability
of exceeding the planned values by 50% for Gamma |
26.274% |
6.649% |
22.558% |
13.094% |
|
21 |
The probability
of exceeding the planned values by 50% for Pareto |
41.366% |
6.649% |
23.405% |
13.802% |
|
22 |
The probability
of exceeding the planned values by 50% for Exponential |
22.471% |
6.009% |
16.408% |
11.111% |
To conclude it is necessary to analyze the overall form of the
distribution of state indicators of oil and gas industry enterprises (Figure
5).
The given distributions demonstrate a
low-frequency specificity of risk when it comes to the oil and gas industry.
However, there are so-called 'long tails' that indicate that the realization of
certain risks can lead to significant losses for the enterprise.
Therefore, it can be concluded that the primary factors for control, in terms of ensuring the sustainability of development. for an oil and gas enterprise are risks of hazardous substance release and destruction of structures. The former are universally significant, while the latter require a systematic analysis of preconditions that will identify minimal fluctuations in their probability of realization.
Figure 5 Gamma Pareto and Exponential distributions of state
indicators of oil and gas industry enterprises
This
research has developed a tool that aggregates the utility of three
distributions (Gamma, Pareto, and Exponential) to describe the probability of an
event with global consequences occurring in a low-frequency (in terms of
frequency of occurrence of such events) environment, whose retrospective
statistical base does not allow for the application of simplified mathematical
description methods. The tool was tested on data on the predisposition of
enterprises in the oil and gas sector to risks - which made it possible to
obtain an effective description of the probability of a breakdown of the
studied system using data containing information about only 36 cases. It
should be noted that within this study,
the analysis was conducted solely based on data from the entire oil and gas
industry in Russia. However,
at the practical level, the use of this toolkit
is most relevant at the specific enterprise level. This assumption is due to
the low frequency of risk events,
which allows for the aggregation of objective and sufficient data solely for
the industry as a whole. In the future, there is a plan to gather more localized risk
statistics within one of the most significant oil and gas industry enterprises
and to test the proposed toolkit in relation to it. The developed model enables
the effective management of risks in the oil and gas industry. mitigating the
occurrence of emergency situations and minimizing the consequences of
accidents. This unique mathematical tool has been crafted for adaptability to a
broad spectrum of practical applications along with an associated algorithm for
its seamless adaptation. The practical results of this study are presented as a
universal risk modeling tool specified to meet the needs of enterprises in the
oil and gas sector. The applicability of these results is determined by the
conclusions resulting from the testing, which
were reflected in decisions regarding changes in the development strategy of a
number of oil and gas enterprises. The limitations of this study undoubtedly
stem from the specifics of the statistical information based solely on data
from the Russian Federation. In future research, it
is advisable to expand the information base for analysis beyond the Russian
Federation and to specify the developed toolkit to the needs of other
industries and types of risks.
The
materials were prepared as part of the implementation of the project of
institutional changes of the strategic academic leadership program “Priority
2030” of the Russian Federation (agreement 075-15-2023-380 dated 02.20.2023).
Biezma, M.V., Andrés. M.A., Agudo. D., Briz. E., 2020. Most Fatal Oil & Gas Pipeline
Accidents through History: A Lessons Learned Approach. Engineering Failure
Analysis, Volume 110, p. 104446
Clare, M.C., Piggott, M.D., Cotter, C.J., 2022. Assessing Erosion and Flood Risk in the
Coastal Zone through the Application of Multilevel Monte Carlo Methods. Coastal
Engineering. Volume 174, p. 104118
Gosnadzor, 2023. Official site of the Gosnadzor. Available online at https://www.gosnadzor.ru/,
Accessed on February 10, 2023
Hartoyo, F., Irianti, G.P., Fatriansyah, J.F., Ovelia, H., Mas’ Ud, I.A, Digita, F.R., Anis. M., 2023. Weibull Distribution Optimization for
Piping Risk Calculation Due to Uniform Corrosion Using Monte Carlo Method. Materials
Today: Proceedings, Volume 80, pp. 1650–1655
Olanipekun, I.O., Alola, A.A., 2020. Crude Oil Production in the Persian Gulf
amidst Geopolitical Risk. Cost of Damage and Resources Rents: Is There
Asymmetric Inference? Resources Policy, Volume 69, p. 101873
Paltrinieri, N., Louise, C., Genserik R., 2019. Learning About Risk: Machine Learning for Risk
Assessment. Safety Science, Volume 118, pp. 475–486
Pishchalkina, I., Pishchalkin, D., Suloeva, S., 2022. Research of the Efficiency of Mining and
Metallurgical Enterprises Based on the Environmental. Social. and Governance
Risk Rating in the Context of Digital Transformation. International
Journal of Technology. Volume 13(7). pp. 1442–1451
Piya, S., Shamsuzzoha, A., Khadem, M., Al-Hinai, N., 2020. Identification of Critical Factors and
Their Interrelationships to Design Agile Supply Chain: Special Focus to Oil and
Gas Industries. Global Journal of Flexible Systems Management, Volume
21, pp. 263–281
Rodionov, D., Kryzhko, D., Tenishev, T., Uimanov, V., Abdulmanova, A., Kvikviniia, A., Aksenov, P., Solovyov, M., Kolomenskii, F., Konnikov, E., 2022. Methodology for Assessing the Digital Image of an Enterprise
with Its Industry Specifics. Algorithms Volume 15(6), p. 177
Ryan, B., Bristow., D.N., 2023. Climate Change and Hygrothermal
Performance of Building Envelopes: A Review on Risk Assessment. International
Journal of Technology, Volume 14(7), pp. 1461–1475
Ting, C., Zakariah, H., Yusri, Y.Z.M., 2022. Probabilistic Risk Assessment of
COVID-19 Patients at COVID-19 Assessment Centre. International Journal
of Technology, Volume 13(6). pp. 1193–1201
Tran, A., Robbe, P., Lim, H., 2023. Multi-Fidelity Microstructure-Induced
Uncertainty Quantification by Advanced Monte Carlo Methods. Materialia, Volume
27, p. 101705
Yang, Haugen, S., Paltrinieri, N., 2018. Clarifying the Concept of Operational
Risk Assessment in the Oil and Gas Industry. Safety science, Volume 108, pp. 259–268
