Multiparametric Optimization of Complex System Management Scenarios Based on Simulation Models
Corresponding email: zhanna.burlutskaya@spbpu.com
Published at : 29 Dec 2023
Volume : IJtech
Vol 14, No 8 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i8.6832
Pospelov, K.N., Burlutskaya, Z.V., Gintciak, A.M., Troshchenko, K.D., 2023. Multiparametric Optimization of Complex System Management Scenarios Based on Simulation Models. International Journal of Technology. Volume 14(8), pp. 1748-1758
| Kapiton N. Pospelov | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Zhanna V. Burlutskaya | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Aleksei M. Gintciak | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
| Konstantin D. Troshchenko | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russia |
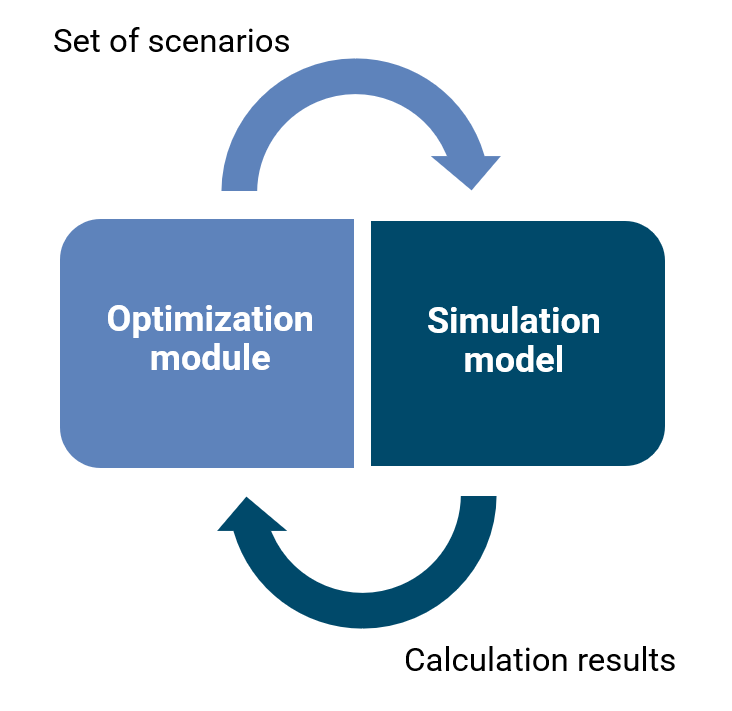
This work is devoted to the development of a
multiparametric optimization module for a digital management decision support
tool based on simulation models. It is noted that the optimization of
simulation models of complex socioeconomic and sociotechnical systems involves
the generation of multiple scenarios of system development, their calculation,
and further comparison, which imposes additional requirements on the
optimization algorithms used. Moreover, complex socioeconomic and
sociotechnical systems are characterized by a multiplicity of goals, which leads to multiparametric
optimization. The result of the work is
the algorithm for solving the problem of optimization of multiparametric
scenario calculations using the example of a two-parameter optimization
problem. The scope of the calculation optimization problem is to form the
optimal set of scenarios that will ensure satisfactory computing time and, at
the same time, give a representative scenario calculation result. Thus, the
contribution of the current research is to formalize the processes of
optimizing the parameters of simulation models of complex systems. In the
course of the study, existing approaches to process optimization are
considered. Based on the analysis of existing approaches to the formation of an
optimal set of scenarios, ways to improve the algorithm type using approaches
to scenario reduction or the introduction of genetic algorithms for the
formation of an optimal set of scenarios are proposed. This work is carried out
within a project to develop a digital tool to support managerial
decision-making in sociotechnical and socioeconomic systems.
Multiparametric optimization; Scenario calculation; Simulation modelling; Stochastic programming
Digital
decision support tools provide an analytical framework for informed managerial
decision-making in sociotechnical and socioeconomic systems based on relevant
and holistic data. This case refers to complex systems that provide both
technical data processing (integrity checking, outlier processing, etc.) and
mathematical modeling considering a variety of computational experiments. Such
scenario calculations are applicable to a wide range of stochastic programming
problems. Computational experiments with simulation models of sociotechnical
and socioeconomic systems are carried out at every stage of the study, from the
study of models to their optimization (Setyaningrum et al., 2022; Rosyidi, Fatmawati,
and Jauhari, 2016). Optimization
of models of complex systems is often associated with the generation of
multiple scenarios of system behavior and their further comparison (Berawi et al., 2018). In turn, this leads to an
increase in the load on the computing power of software tools that control the
model and its results.
The analysis of existing theoretical and practical research in the domain of production process optimization is indisputably crucial in the initial phase of the study. However, the specifics of the study require a clear statement of the task upon which the selection of pertinent sources will depend.
2.1. Description of a typical optimization problem of multiparametric
scenario calculation in stochastic programming
A typical problem solved using the proposed methods is a multiparametric
optimization with a set of scenarios, usually represented by a set of values of
n variables, which can be either discrete or continuous.
In this case, it is possible to represent a set of scenarios as a bounded set for discrete parameters, the number of elements of which is S.
In the formula (1) ki is the number of acceptable (considered) values of
the i-th parameter from the set of discrete values that the parameter can
accept.
For the
case with at least one continuous variable in the number of scenario
calculation parameters, it is obvious that
In the
scenarios under consideration, the optimization task involves narrowing down
the initial set S to a set So. The objective is to ensure that the number of
elements in this set does not exceed the threshold needed for a computationally
efficient process, while keeping the computational error, associated with a
reduction in the accuracy of calculations, below a specified level. Formally,
the task at hand can be expressed as a mathematical transformation of equation
(2).
The task core challenge is the
impossibility of accurately determining the representativeness criteria of a
set of scenarios: if the computational time is predictable at a sufficient
confidence level (i.e. an upper bound for the number of scenarios in the
optimal set can be determined with some accuracy), then the degree of
representativeness cannot be accurately estimated (which leads to uncertainty
of the lower bound for the number of scenarios in the optimal set).
The
hypothesis of the present study is the possibility of implementing such a
transformation with a significant reduction in computational time for an optimal
set of scenarios and maintaining a level of representativeness comparable to
the original set of scenarios in the case of a general multiparametric
optimization problem in stochastic programming.
2.2. Methods of forming an
optimal set of scenarios. General information and algorithms
As part of the study, an
analysis of existing theoretical and practical research in the field of multiparametric
optimization of forming an optimal set of scenarios was
carried out. The analysis is based on articles from the Scopus database of
scientific publications over the past 5 years. The following keywords were used
during the selection of sources: optimization algorithm; multiparametric
optimization; scenario calculation; simulation modeling; stochastic programming.
The stochastic optimization method utilizes randomness
in the search for an optimum. Thus, when simulating the system's probabilistic
features to model uncertainty, random distributions are included as input data (Zakaria et al., 2020; Wang, Liu, and Kirschen, 2017). Owing to the increasing number
of scenarios, the scenario reduction technique is employed, enabling control of
the computational burden by selecting representative scenarios for subsequent
optimization. Nonetheless, this method has drawbacks, including the fact that
the user must determine the number of representative scenarios as a parameter (Wang, Liu,
and Kirschen, 2017).
Due to the complexity of multi-criteria optimization
of production processes, the use of artificial intelligence methods has surged
in popularity over the last few years (Sibalija, 2018). Metaheuristic approaches to optimization stand out for their higher
computational accuracy and the capability to search for both local and global
optima, setting them apart from traditional mathematical approaches.
The simulated annealing algorithm is utilized for
optimizing production process parameters and serves as an illustration of Monte
Carlo methods employed to study numerical processes. The method belongs to the
group of metaheuristic search methods and is considered part of artificial
intelligence. The algorithm starts by selecting an initial point at random
whilst at high temperature. If the new point's objective function exceeds the
current one, another point is selected. When the temperature reaches its
minimum, the chances of selecting the worst points become negligible,
indicating that the algorithm converges to the optimal solution (Sibalija, 2018).
Two metaheuristic methods based on natural or animal
behavior, namely genetic algorithms (GA) and the particle swarm method (PSO),
are explored in this section. This approach also utilizes optimization methods
such as ant colony optimization (ACO) and artificial bee colony (ABC).
Evolutionary algorithms for multi-criteria
optimization based on decomposition simplify a multi-criteria problem by
breaking it down into a set of single-criteria optimization tasks through the
combination of criteria in various ways. This approach divides the initial
criteria into subsets using scalarization with uniformly dispersed direction
vectors before jointly optimizing these subsets (Wu et
al., 2022;
Hong et al., 2019). It facilitates the inclusion of
nonlinearity, variable mixing, and other factors (Cai,
Qu, and Cheng, 2018). There
are additional algorithms that combine criteria, utilize indicators, and focus
on the dominance ratio. Genetic algorithms are a type of heuristic method for
finding the extremum. This approach implies the random generation of a set of
solutions and their evolution, promoting the survival of those solutions most
likely to produce an optimal result after a certain number of iterations.
In the presence of numerous variations in the system
state, conventional scenario-based optimization methods may prove less
effective in achieving optimal result accuracy while also demanding substantial
computational time and power resources. Conversely, an alternative approach
that does not provide guaranteed accuracy but instead yields optimal or
near-optimal results in practice may offer a more efficient solution. The
algorithm's fundamental principle entails creating a random initial
"population" of scenarios and subsequently selecting the
"fittest" of them through evolutionary means. "Fitness" is
determined by a corresponding function specifically set for solving the problem
at hand. After a sufficient number of iterations of such selection, it is possible
to attain an optimal "population".
Genetic algorithms are a commonly employed tool in
tackling various specific problems, such as those found in administration and
management. Nevertheless, the majority of issues resolved by means of such
methods are characterized by a deterministic environment, where probabilistic
traits (which inevitably exist in these situations, at the very least as the
probability of "mutation" or "crossover" for a
"population" of scenarios) possess the only and most precise value. At the
same time, in certain instances of employing this approach, events are
considered probabilistic, like the influence of the fitness function's value on
an individual's 'probability' of survival (for instance, when chosen from a
uniform distribution in the selection function). This contrasts with their
survival in a deterministic sense. Consequently, the use of genetic algorithms
represents a promising approach in dealing with probabilistic environments.
Such algorithms enable the rapid selection of quasi-optimal scenarios. The
potential consideration of probabilities, which are not usually excluded from
the toolkit of genetic algorithms, indicates the applicability of such methods
for addressing the problem at hand. A large number of diverse applications of
genetic algorithms provide further justification for employing this approach.
The particle swarm optimization method is a heuristic
technique for global optimization. It relies on simulating the motion of
numerous particles (a swarm) in a multidimensional space to achieve the optimal
position. A noteworthy characteristic of this approach is its lack of reliance
on gradients, which positions it as a dependable stochastic optimization
algorithm from the lower sensitivity perspective. For combinatorial and nonlinear optimization,
a hybrid approach is employed, combining the sequential use of algorithms for
simulated annealing and swarming particles. This approach aims to enhance the
efficiency of optimization by locating the position of the swarm of particles
and their best social behavior. The method of simulated annealing is used to
determine the optimal global position. The hybrid algorithm enables the
solution performance to be independent of the starting point selected and
offers improved stability and rapidity in locating the global optimum point (Javidrad et al., 2017).
The utilization of artificial neural networks in
conjunction with simulated annealing algorithms and the particle swarm method
in time series forecasting models yields the best results for optimizing
process parameters. Also, it is advisable to combine annealing simulation
methods and genetic algorithms to enhance optimization efficiency.
In multi-criteria optimization, the Pareto optimal
solution method is a principal approach that employs scalarization techniques
to obtain optimal results. The optimal value in multi-criteria optimization is
achieved when one objective function cannot increase without decreasing the
other objective function. This condition is called Pareto optimality (Gunantara, 2018).
When the priority of criteria is not specified, the
global criterion method is used. It enables uniform priority across all
functions by identifying the optimal vector that minimizes a global criterion.
The weighted sum method is also employed to tackle multi-criteria optimization
tasks by merging varied criteria into a unified goal. Nevertheless, the
method's drawback is the challenge presented in selecting task-specific
weights.
Each of
the approaches can be applied to optimize probabilistic events and, therefore,
presumably adapted to optimize simulation models. However, considering the
complex structure of socioeconomic and sociotechnical systems, as well as their
variability, it is imperative to opt for the most versatile solution. This
solution will not necessitate integration into the model's structure but will
permit external circuit control. Thus, optimization will not depend on the
structure of the model but will work with a set of behavior scenarios instead.
Scenario reduction and genetic algorithms were selected out of all the options
examined. The selected options are essentially counterparts to simpler
(scenario reduction) and more sophisticated (genetic algorithms) approaches.
So, consider general
algorithms.
Figure 1 demonstrates a general scenario reduction
algorithm based on information from sources (Kammammettu
and Li, 2023; Peredo and Herrero, 2022; Dvorkin et al., 2014). Scenario reduction, as outlined by Tarasov (2016), encompasses
techniques aimed at filtering out potentially unrepresentative elements from
the initial set of scenarios to form an optimal one. The simplest method for
scenario reduction is random sampling.
Genetic algorithms are opposed to the above scenario
reduction algorithm (Alam et al., 2020). Figure 2 shows the general algorithm for searching the optimal set of
scenarios based on information from sources.
Figure 1 Scenario reduction algorithm general layout
Figure 2 Search for the optimal set of scenarios via a genetic
algorithm general layout
The algorithms considered are almost identical, even
though the proposed methods are based on completely different prerequisites.
Thus, scenario reduction is based on the formation of a large set of scenarios
for input and the establishment of a criterion for the number of scenarios (Oliveira, Carravilla, and Oliveira, 2022; Heitsch and Römisch, 2007), and genetic algorithms assume the ability to set the
initial set of scenarios in the volume corresponding to the volume of the
optimal set of scenarios (i.e., the volume search problem needs to be solved).
Scenario reduction assumes a quantitative criterion as a criterion for
terminating iterations, while a genetic algorithm assumes an abstract
representativeness criterion, the calculation methods of which are the subject
of a separate study. Despite the obvious advantages of integrating the
considered methods, it is important to understand that none of them guarantees
finding the absolute optimum. It's time to move on to the formalization of optimizing the parameters of
simulation models of complex systems.
The developed prototype solves the problem of two-parameter optimization by a set of interrelated input parameters. Regarding the problem, it should be noted that the input parameters have different types: integers and fractional numbers from continuous ranges or finite discrete sets. This remark allows us to declare the applicability of the prototype on the entire class of similar tasks without reference to the input data type. The problem optimality criterion includes two output parameters. Due to the requirements for consistent optimization, the solution must be a Pareto front. The algorithm of the prototype is iterative and connected with a software module that executes scenario calculation. Figure 3 shows the algorithm's general layout.
Figure 3 Scenario calculation optimizer algorithm
In conditionally independent
groups, dominant parameters are specifically identified. The values of these
parameters influence the potential sets of values for the remaining parameters
within the group.
At the end of data preparation,
groups of conditionally independent parameters are divided into subgroups
according to the possible values (or ranges of values for continuous
parameters) of the dominant parameters: each subgroup must differ from all
others by at least one value of at least one dependent on the dominant
parameter. We call sets of subgroups formed from one group a line.
At the stage of scenario generation, one subgroup is randomly selected from each line, and parameter values (both dominant and dependent on them) that satisfy the conditions of the subgroup are randomly set. Expert assignment of weights to certain subgroups in the lines is allowed to increase the probability of empirically choosing more common values of the dominant parameters. Likewise, the values of independent parameters are randomly set. The result is a set of parameters for scenario calculation. Then, the algorithm accesses the scenario calculation program. At the output, the obtained value is checked in accordance with the Pareto criterion. The iterative comparison procedure includes an evaluation of the resulting point at this iteration from each of the points of the Pareto front formed based on the results of past iterations. If the values of at least one of the objective functions deteriorate, the resulting point is excluded from consideration. When improving the values of one of the objective functions and preserving the value of the other objective function, the resulting point is added to the Pareto front. When the values of both objective functions are improved, the resulting point is added to the Pareto front, and the point compared with it is excluded from the Pareto front. If the Pareto front is empty (first iteration), the resulting point is added to the Pareto front. Iterations continue until the specified value of the iteration termination criterion is reached. Within the prototype, such a criterion is the number of iterations.
Discussion
The problem raised in this study,
namely the consideration of uncertainty in multiparametric optimization
problems, has been widely presented in scientific publications of the last ten
years (Pappas et al., 2021). So, researchers take into account uncertainty by modeling the
parameters themselves. That is, integer variables are treated as uncertain
parameters, and the problem is solved through polynomial functions (Charitopoulos, Papageorgiou, and Dua, 2018). Thus, the problem of accounting for uncertainty is
reduced to the problem of linear programming, which is generally characteristic
of many other studies (Pappas et al., 2021). An alternative to linear programming is the approach
of describing the problem and solving it through partial differential equations
(Petsagkourakis and Theodoropoulos, 2018). Each of the solutions has its
own capabilities and disadvantages, but they are all characterized by the
strict mathematical formalization of systems limited in complexity, as well as
the impact on the characteristics of the system parameters, i.e., the
introduction of uncertainty deep inside the model. We propose to solve the
problem of uncertainty in the system through external control of the simulation
model of the system. This approach makes it possible to separate optimization
and simulation of the system, which simplifies overloaded complex models of
systems and logically separates two interrelated but very different tasks:
system simulation and system optimization.
Comparing the algorithm we have developed
with other similar studies, it is worth noting that we do not focus on the
cause-effect relationships between the parameters (Seeve et
al., 2022). On the one hand, this feature
makes it possible to achieve the universality of the algorithm, but on the
other hand, it potentially reduces its accuracy for more deterministic systems (Seeve et al., 2022). This
issue requires further investigation.
The proposed algorithm can be improved in accordance
with the principles proposed in the Methods section. At this point, the
algorithm implements a random selection of scenarios based on dependent
datasets, which, as expected, gives a more representative set of scenarios than
a simple random sample of scenarios. However, even such an approach cannot
fully satisfy the need for the formation of a representative set of scenarios
while reducing the calculation time.
Ways
to improve the algorithm consist of integrating elements of scenario reduction
and/or genetic procedures into it, aimed together at forming an optimal
scenario with a higher probability than the existing method based on
randomness. At this stage of the study, an
assumption is made about the prospects of using genetic algorithms not due to
their dominance over other methods but because of their popularity among
researchers and successful application in a greater number of cases. However,
at the next stage of the study, it is necessary to conduct a full-fledged
in-depth analysis of evolutionary algorithms, as well as a series of
experiments on real data. It is important to note that even though the
described algorithm is implemented in software and tested on synthetic data,
its applicability to real data has yet to be verified, which is the main task
in the framework of the continuation of the project.
The result of the work is the developed prototype of a
scenario calculation optimization algorithm for the problem of two-parameter
optimization as a module for a digital tool to support managerial
decision-making in sociotechnical and socioeconomic systems. In the case of the study, the
problem of optimizing a set of scenarios is formalized, general ideas are
formed about two opposed problem-solving methods (scenario reduction and
genetic search for the optimal set), an algorithm for addressing the general
problem of multiparametric optimization is proposed (providing the example of
two-parameter optimization). The ways of improving the algorithm prototype
using approaches to scenario reduction or implementing evolutionary algorithms
for the optimal set of scenario formation are considered. In the next stage of the study, a
comprehensive in-depth analysis of evolutionary algorithms is planned, along
with a series of experiments on real data. This is necessary as the current
results are confined to theoretical prerequisites. Thus, the contribution of
the current research is to formalize the processes of optimizing the parameters
of simulation models of complex systems. The research is carried out within a project to develop a
digital tool to support managerial decision-making in sociotechnical and
socioeconomic systems.
The research is funded by the Ministry of Science
and Higher Education of the Russian Federation (contract No. 075-03-2023-004
dated 13.01.2023).
Alam, T., Qamar, S.,
Dixit, A., Benaida, M., 2020. Genetic Algorithm: Reviews, Implementations, and
Applications. International Journal of Engineering Pedagogy, Volume 12,
pp. 57-77
Berawi, M.A., Nabila, A.,
Gunawan., Miraj, P., Abdul Rahman, H., Berawi, A.R.B., 2018. Analysis of Life
Cycle Cost and Public-Private Partnership in the Development of Walini City as
Technology Park. International Journal of Technology, Volume 9(7), pp.
1469–1479.
Cai, L., Qu, S., Cheng, G., 2018.
Two-Archive Method for Aggregation-Based Many-Objective Optimization. Information
Sciences, Volume 422, pp. 305–317
Charitopoulos, V.M.,
Papageorgiou, L.G., Dua, V., 2018. Multiparametric Mixed Integer Linear
Programming Under Global Uncertainty. Computers & Chemical Engineering,
Volume 116, pp. 279–295
Dvorkin, Y., Wang,
Y., Pandzic, H., Kirschen, D., 2014. Comparison of Scenario Reduction
Techniques for the Stochastic Unit Commitment. In: 2014 IEEE PES General
Meeting, pp. 1–5
Gunantara, N., 2018. A Review of
Multi-Objective Optimization: Methods and its Applications. Cogent
Engineering, Volume
5, p. 1502242
Heitsch, H., Römisch,
W., 2007. A Note on Scenario Reduction for Two-Stage Stochastic Programs. Operations
Research Letters, Volume 35, pp. 731–738
Hong, W., Tang, K.,
Zhou, A., Ishibuchi, H., Yao X. A Scalable Indicator-Based Evolutionary
Algorithm for Large-Scale Multiobjective Optimization. IEEE Transactions on
Evolutionary Computation, Volume 23, pp. 525–537
Javidrad,
F., Nazari, M., 2017. A New Hybrid Particle Swarm and Simulated Annealing
Stochastic Optimization Method. Applied Soft Computing, Volume 60, pp. 634–654
Kammammettu, S., Li,
Z., 2023. Scenario Reduction and Scenario Tree Generation for Stochastic
Programming Using Sinkhorn Distance. Computers and Chemical Engineering,
Volume 170, p. 108122
Oliveira, B.B.,
Carravilla, M.A., Oliveira, J.F., 2022. A Diversity-Based Genetic Algorithm for Scenario Generation. European
Journal of Operational Research, Volume 299, pp. 1128–1141
Pappas, I., Kenefake,
D., Burnak, B., Avraamidou, S., Ganesh, HS., Katz, J., Diangelakis, NA.,
Pistikopoulos, EN., 2021. Multiparametric Programming in Process Systems
Engineering: Recent Developments and Path Forward. Frontiers in Chemical
Engineering, Volume 2, p. 620168
Peredo, O.F., Herrero, J.R., 2022. Acceleration Strategies for Large-Scale
Sequential Simulations Using Parallel Neighbour Search: Non-LVA and LVA
Scenarios. Computers and Geosciences, Volume 160, p. 105027
Petsagkourakis, P., Theodoropoulos,
C., 2018. Data Driven Reduced Order Nonlinear Multiparametric MPC for Large
Scale Systems. Computer Aided Chemical Engineering, Volume 43, pp. 1249–1254
Rodionov, D.G.,
Alfer'yev, A.D., 2020. Sustainability of The Optimal Plan of Innovative
Production of An Industrial Enterprise. St. Petersburg State Polytechnical
University Journal. Economics, Volume 13(5), pp. 106–119
Rosyidi, C.N.,
Fatmawati, A., Jauhari, W.A., 2016. An Integrated Optimization Model for
Product Design and Production Allocation in a Make to Order Manufacturing
System. International Journal of Technology, Volume 7(5), pp. 819–830
Seeve, T., Vilkkumaa
E., 2022. Identifying and Visualizing a Diverse Set of Plausible Scenarios for
Strategic Planning. European Journal of Operational Research, Volume 298
(2), pp. 596–610
Setyaningrum, R.,
Subagyo, Wijaya, A., 2022. A Mathematical Model of Successful-Product
Development by Considering the Indonesian Culture. International Journal of
Technology, Volume 13(3), pp. 655–663
Sibalija,
T., 2018. Application of Simulated Annealing in Process Optimization: A Review.
Nova Science Publishers, Simulated Annealing: Introduction, Applications and Theory, Volume 2018, pp. 1–14
Simsek, E., Demirel,
Y.E., Ozturk, E., Kitis, M., 2022. Use of Multi-Criteria Decision Models for
Optimization of Selecting The Most Appropriate Best Available Techniques in Cleaner
Production Applications: A Case Study in a Textile Industry. Journal of
Cleaner Production, Volume 335, p. 130311
Wang, Y., Liu, Y., Kirschen,
D.S., 2017. Scenario Reduction with Submodular Optimization. IEEE Transactions on Power Systems, Volume 32, pp. 2479–2480
Wu, T., An, S., Han, J., Shentu,
N., 2022. An -domination Based Two-Archive 2 Algorithm for Many-Objective
Optimization. Journal of Systems Engineering and Electronics, Volume 33, pp. 156–169
Zakaria,
A., Ismail, F.B., Lipu, M. H., Hannan, M.A., 2020. Uncertainty
Models for Stochastic Optimization in Renewable Energy Applications. Renewable
Energy, Volume 145, pp. 1543–1571
