Integrating Data Mining Techniques for Fraud Detection in Financial Control Processes
Corresponding email: vmsushkov@mephi.ru
Published at : 29 Dec 2023
Volume : IJtech
Vol 14, No 8 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i8.6830
Sushkov, V.M., Leonov, P.Y., Nadezhina, O.S., Blagova, I.Y., 2023. Integrating Data Mining Techniques for Fraud Detection in Financial Control Processes. International Journal of Technology. Volume 14(8), pp. 1675-1684
| Viktor M. Sushkov | Department of Financial Monitoring, National Research Nuclear University MEPhI, Kashirskoe shosse, 31, Moscow, 115409, Russia |
| Pavel Y. Leonov | Department of Financial Monitoring, National Research Nuclear University MEPhI, Kashirskoe shosse, 31, Moscow, 115409, Russia |
| Olga S. Nadezhina | School of Industrial Economics, Peter the Great St. Petersburg Polytechnic University (SPbPU), Polytechnicheskaya, 29, Saint Petersburg, 195251, Russia |
| Irina Y. Blagova | School of Industrial Economics, Peter the Great St. Petersburg Polytechnic University (SPbPU), Polytechnicheskaya, 29, Saint Petersburg, 195251, Russia |
Detecting fraud in financial control processes
poses significant challenges due to the complex nature of financial
transactions and the evolving tactics employed by fraudsters. This paper
investigates the integration of data mining techniques, specifically the
combination of Benford's Law and machine learning algorithms, to create an
enhanced framework for fraud detection. The paper highlights the importance of
combating fraudulent activities and the potential of data mining techniques to
bolster detection efforts. The literature review explores existing
methodologies and their limitations, emphasizing the suitability of Benford's
Law for fraud detection. However, shortcomings in practical implementation
necessitate improvements for its effective utilization in financial control.
Consequently, the article proposes a methodology that combines informative
statistical features revealed by Benford’s law tests and subsequent clustering
to overcome its limitations. The results present findings from a financial audit
conducted on a road-construction company, showcasing representations of
primary, advanced, and associated Benford’s law tests. Additionally, by
applying clustering techniques, a distinct class of suspicious transactions is
successfully identified, highlighting the efficacy of the integrated approach.
This class represents only a small proportion of the entire sample, thereby significantly
reducing the labor costs of specialists for manual audit of transactions. In
conclusion, this paper underscores the comprehensive understanding that can be
achieved through the integration of Benford's Law and other data mining
techniques in fraud detection, emphasizing their potential to automate and
scale fraud detection efforts in financial control processes.
Benford’s Law; Clustering; Ellipsoidal approximation; Isolation forest; Principal component analysis
In today's
digital age, where financial crimes and illicit activities have become
increasingly sophisticated, fraud detection is one of the most important
functions of financial control entities. As technology advances, fraudsters
adapt their methods, making it necessary to integrate advanced data mining
techniques to improve fraud detection capabilities.
Despite the large number of data mining techniques studied to date, only a few are most applicable to financial fraud detection. This research aims to address the limitations of existing approaches in applying data mining techniques to fraud detection and propose a comprehensive methodology that can be universally applied to numerical financial data. By combining the power of advanced data mining techniques with Benford's Law, financial control entities can enhance their ability to detect and prevent fraudulent activities, safeguarding their financial integrity and protecting stakeholders' interests.
2.1.
Literature Review
The statistical
method, commonly referred to as Benford's Law or the Law of Anomalous Numbers,
is gaining significant traction in global financial control practices.
According to this law, in datasets generated through natural processes and
without deliberate human manipulation, the distribution of first digits should
conform to a discrete exponential distribution, commonly known as Benford's
distribution (Nigrini, 2012).
The use of
Benford's Law is justified by the unique characteristics of financial fraud.
Fraudulent activities often involve intentional manipulation of financial data,
such as falsifying transactions, inflating revenues, or understating expenses.
However, they often leave subtle, unintentional traces that go against the
expected patterns in naturally occurring data. Fraudulent numbers, often
manipulated by humans, tend to deviate from the expected distribution outlined
by Benford's Law. This deviation serves as a red flag, alerting financial
control entities to the potential presence of fraud.
The greatest
contribution to the development of Benford's Law was made by Professor Mark
Nigrini, who proposed a methodology for the integrated application of Benford’s
Law tests to detect financial fraud (Nigrini, 1993; Nigrini, 2012). Validation of the tests proposed by Mark
Nigrini on different sets of corporate data proves their effectiveness in terms
of identifying anomalies in large sample populations (Leonov
et al., 2021; Rad et al., 2021; Manuel and Garcia, 2021; Pupokusumo et al., 2022). The adaptable nature of
Benford's law allows it to be combined with other statistical approaches, which
has been done in previous research with neural networks, logistic regression,
decision trees, and random forests (Bhattacharya, Xu and Kumar, 2011; Badal-Valero, Alvarez-Jareño, and Pavía, 2018; Bhosale and
Troia, 2022). In some cases, however, the results obtained by Benford’s Law
tests may be contradictory and ambiguous (Ergin and Erturan, 2020; Leonov et al., 2022; Fernandes and Antunes, 2023), which points to the need to
improve the methodology.
2.2.
Methodology
The
recognition of the law can be attributed to the publication of a comprehensive
study conducted by American engineer Frank Benford in 1938 (Nigrini, 2012). That is why the law is now
commonly referred to as Benford's Law, despite it being originally discovered
by American astronomer S. Newcomb. Benford's research was supported by
extensive analysis of the frequencies of first digits in 20 diverse datasets,
encompassing areas such as geography, demographics, physics, mathematics, and other accumulated
data. The majority of these examples provided further evidence of the law's
validity. Additionally, Benford made a significant contribution by developing
formulae for determining the probabilities of the first (), second (
), and the first two (
)significant digits in any number system (
) (formulae 1-3). In practice, problems
solved using Benford's law predominantly relate to the decimal number system,
hence the utilization of the decimal logarithm in these formulae (
= 10).
American researcher M. Nigrini presented a
comprehensive approach for assessing numerical data sets based on Benford's law
(Nigrini, 2012). His methodology includes three categories of
statistical tests: basic, advanced, and associated. The selection of specific
tests from these categories depends on the problem under investigation as well
as the quantity of available data. Typically, the tests are conducted in a
sequential manner, starting with basic tests and then progressing to advanced
and associated tests.
Basic tests, including the first digit test, second
digit test, and first two digits test (also known as the first order test) are
the fundamental and commonly used tests based on Benford's law. They are
conducted separately on positive and negative numbers due to variations in the
motives behind their manipulation. For instance, it is observed that management
often exaggerates profits but underestimates losses.
Advanced tests, including the summation test and the
second-order test, perform a deeper analysis. According to M. Nigrini, these
tests can be performed on almost any data set, even if it is assumed that they
will not comply with Benford's law (Nigrini, 2012). Preliminary filtering is not required to perform advanced tests.
Associated tests include the number duplication
test, the last digits test, and the distortion factor model. These tests are
additional and are based not on Benford's law but on other features of the
numerical distribution.
The goodness of fit of the actual distribution to
Benford's one is estimated not only empirically but also quantitatively. In
this regard, statistical characteristics are calculated, each with specific
applications and interpretations. One of the most widely utilized is
Z-statistics, which entails the comparison of the empirical and theoretical
frequencies of a particular digit. The magnitude of deviations directly
corresponds to the level of suspicion, with higher deviations indicating a
greater degree of anomaly (Nigrini, 2012).
Nevertheless, the methodology proposed by M. Nigrini
has several limitations and shortcomings that necessitate improvements for
practical implementation in financial control.
Firstly, the application of various methods to test
the conformity of the sample distribution to the Benford distribution often
yields contradictory results. For instance, the chi-square is rather
categorical and frequently indicates non-compliance with the Benford
distribution, even when the visual similarity between the sample distribution
and the theoretical one suggests otherwise. The mean absolute deviation (MAD)
may confirm acceptable or close conformity to the Benford distribution for the
same dataset. This discrepancy arises due to the chi-square’s dependence on
sample size, unlike the mean absolute deviation, making the latter a more
preferable and reliable statistic.
Secondly, it is not uncommon for Z-statistics to
exceed critical values, while other methods indicate compliance with the
Benford distribution when analyzing real data. To address this issue, widening
the confidence interval for Z-statistics by increasing the confidence
probability is necessary. However, deviating from the standard 95% confidence
level is not recommended and should be avoided.
Furthermore, advanced tests, such as the summation
and second order tests, are difficult to interpret, and it is challenging to
form samples of suspicious transactions based on them. These tests involve
complex statistical calculations and may require a deep understanding of
mathematical concepts. As a result, it can be difficult for auditors or
investigators to accurately identify suspicious transactions based on the
results of these tests.
Finally, when dealing with large volumes of data,
Nigrini's suspiciousness selection method still leaves significant samples that
require further processing. Additional computational resources and advanced
data processing techniques may be necessary to process these results
effectively.
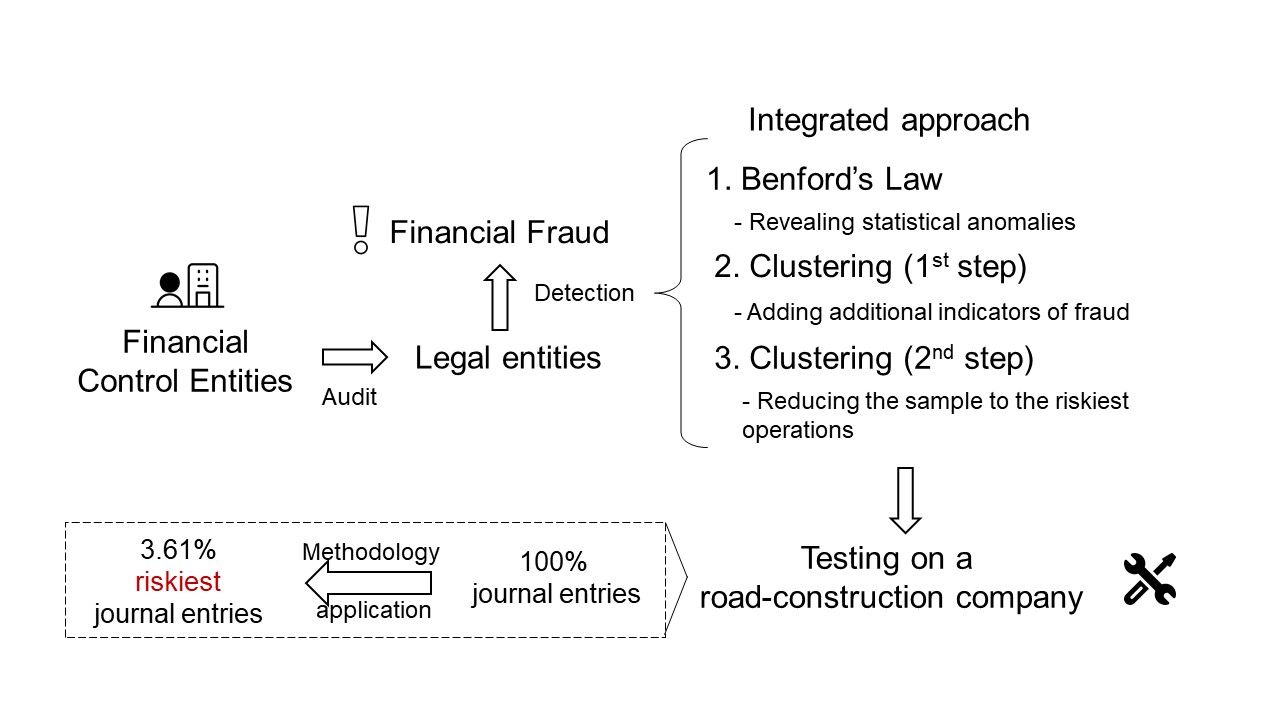
To overcome the aforementioned problems, a potential solution is to combine the most informative statistical features and perform clustering based on them. The proposed methodology begins by implementing basic, advanced, and associated Benford's Law tests and calculating statistical characteristics based on them. Then, clustering algorithms are applied to identify sets of potentially risky transactions that deviate from expected patterns and are more likely to contain fraudulent activity. Additionally, the transactions are clustered based on other fraud indicators such as debit and credit frequency, weekend transactions, and reversal transactions to further narrow down their volume. The result is a subset of high-risk transactions that require manual examination by financial control specialists.
Results
We validated the improved methodology in a series of
financial audits and chose to present the findings from an audit conducted on a
road-construction company as it is one of the most representative cases. The
data to be analyzed is an array of journal entries for three years, containing
27 attributes and 1,459,270 records. The attributes included the accounts,
documents, contents, amounts, and other transaction details. To ensure
confidentiality, all names and sensitive information have been changed.
The array was then checked against the requirements that need to be met in order for Benford’s Law to be used. These include random formation, sufficient volume, absence of categorical data, no minimum and maximum limits, proximity to an exponential distribution, etc. The array has been verified, and therefore, it was decided to examine the whole set of journal entries over the period, consistently using the primary, advanced, and associated tests. The confidence level at which the tests were conducted is 95%, which is usually used in Benford’s Law analysis.
Graphical representations of the results of some primary, advanced, and
associated tests are shown in Figures 1, 2 and 3, respectively. From the visual
analysis, deviations from the expected theoretical frequencies can already be
observed.
Figure 1 Results of
the a) First digit test; b) First-order test
Figure 2 Results of the a) Second-order test; b) Summation test (for the first pair of digits)
Figure 3 Results of
the a) Number duplication test; b) Last two digits test
In order to
conduct further analysis aimed at detecting potentially fraudulent
transactions, it was decided to partition the dataset into distinct classes.
The clustering process will be carried out based on the outcomes of Benford's
law tests, including:
·
Z-statistics
for the first digit test;
·
Z-statistics
for the second digit test;
·
Z-statistics
for the first-order test;
·
Sums of
digit frequencies from the summation test;
·
Z-statistics
for the second-order test;
·
Frequency of
transaction amounts.
The silhouette method was used to visually estimate the number of clusters into which the sample should be divided (Figure 4). This method helps to evaluate the quality of clustering by measuring how similar an object is to its own cluster compared to other clusters.
Figure 4 Silhouette
graph
The number of classes is selected by the maximum silhouette value. In this case, it was decided to split the sample into 2 classes. As a result of the division, class 0 included 34,753 objects, and class 1 included 9,030 objects. A plot of means for each cluster is shown in Figure 5. The x-axis represents the features on which clustering was conducted, while the y-axis displays the averaged values within each class.
Figure 5 Plot of
means
The figure
shows that class 1 is characterized by higher mean values for each feature
compared to cluster 0. In addition, class 1 contains a smaller number of
objects. Hence, we can assume that suspicious operations were allocated to the
1 cluster.
A visualization in principal components was also constructed for the obtained classes. Principal component analysis is used to show the relationships and patterns among the different classes or groups in the data. Figure 6 shows that the two clusters do not overlap.
Figure 6 Visualisation in principal components
In order to
identify outliers, two algorithms were utilized – Isolation Forest and
Ellipsoidal Approximation. Figures 7 and 8 show the labels assigned by each
method based on statistical characteristics.
The
isolating forest highlighted most of the Class 1 representatives in the
outliers (Figure 7).
Figure 7 Result of
the isolation forest
The ellipsoidal approximation also highlighted some of the objects in cluster 1 as outliers, but a smaller part of it compared to the previous algorithm (Figure 8).
Figure 8 Result of
the ellipsoidal approximation
In Figure 9, the dotted line shows the mean values of the features for the class consisting of objects that were selected as outliers by both algorithms. Cluster 1 is similar to the class consisting of outliers. Hence, we can conclude that class 1 does contain suspicious operations.
Figure 9 Plot of
means for selected classes and the class of outliers
For the
analysis of the suspicious class, we conducted additional clustering based on
the following features:
·
Debit account frequency;
·
Credit account frequency;
·
Transaction frequency;
·
Author frequency;
·
Manual transactions;
· Weekend or
weekday transactions;
·
Reversal transactions;
·
Duplicate count.
The number of classes is also determined by the silhouette method (Figure 10).
Figure 10 Silhouette graph for suspicious transactions
Figure
10 shows that the most successful partitioning will be when the number of
classes is 5. As a result, class 0 includes 937 objects. The first class
includes 69 objects, the second class includes 174 objects, the third class
includes 80 objects, and the fourth class includes 446 objects. The mean values
for the new clusters are shown in Figure 11.
Figure 11 Plot of means for the new clusters
Discussion
We proceeded to analyze the outcomes of clustering applied to the suspicious transactions category. This examination is aimed at extracting meaningful insights regarding the underlying patterns and characteristics of the identified clusters.
The analysis
reveals that the 0 cluster is the largest in terms of the number of objects.
This observation can be attributed to the intermediate mean values observed
across all attributes within this cluster. Objects belonging to class 1 exhibit
the highest mean value for the attribute "Author frequency". Class 2
demonstrates the highest mean value for the attribute "Credit account
frequency". Class 3 is characterized by a high mean value for the
attribute "Transaction frequency" and the lowest mean value for the
attribute "Author frequency". Finally, objects in class 4 present the
highest mean value for the attribute "Weekend or weekday
transaction".
As a result,
we successfully identified a class of suspicious transactions that encompassed
a total of 52,706 objects, equivalent to 3.61% of the entire sample. This
indicates that a small but significant proportion of the transactions exhibited
characteristics that warranted further investigation due to their suspicious
nature.
In the
selected operations, the following signs of potential fraud were identified:
1. Unusual
transaction patterns;
2. Misrepresentation
of expenses;
3. Unauthorized
transactions;
4. Overbilling
or double billing;
5. Collusion
with vendors or subcontractors;
6. False
reporting and documentation;
7. Inadequate
internal controls.
While
studies in the past two decades have demonstrated the effectiveness of
Benford's Law for fraud detection, the current work provides a more
comprehensive and efficient approach to financial fraud detection by deepening
previous research and combining Benford’s Law with other data mining
techniques. The universal character of the methodology allows it to be applied to
various types of numerical financial data, unlike specific neural networks,
logistic regression, and random forest models.
The proposed methodology allows
for more efficient and targeted examination of suspicious transactions,
minimizing the labor-intensive task of manual auditing for all transactions.
Moreover, this study addresses the specific requirements of examining accounting
records within the context of financial control measures. By considering the
unique characteristics of this domain, the methodology is tailored to
accurately identify potential fraudulent activities in financial transactions.
The
application of data mining techniques in financial control activities has
indeed been proven to enhance organizational efficiency. By automating routine
transaction checks, professionals can allocate their time and resources to more
critical operations that require additional scrutiny. This not only improves
the overall efficiency of the organization but also ensures that suspicious
transactions with significant monetary values are identified promptly. The combination of
Benford's Law with other machine learning techniques provides a unique
perspective on data analysis for fraud detection. This integration allows for a
more comprehensive understanding of patterns and anomalies in financial data.
By leveraging the power of machine learning algorithms, the application of
Benford's Law can be automated and scaled, making it a valuable tool for
large-scale fraud detection efforts. However, while data
mining techniques have shown promise in detecting potential fraud, there is
always a need to refine and improve the algorithms to reduce false positives
and negatives. In addition, this approach relies on historical patterns and may
struggle to detect new or evolving forms of fraud. To mitigate these
limitations, further research is needed to optimize machine learning algorithms
for processing large volumes of journal entries and enhance the accuracy of
identifying suspicious transactions. Evaluation and refinement of the models
will help achieve better results in identifying signs of fraud.
The
research was funded by the Ministry of Science and Higher Education of the
Russian Federation under the strategic academic leadership program “Priority
2030” (Agreement 075-15-2023-380 dated 20.02.2023).
Badal-Valero, E., Alvarez-Jareño, J.A., Pavía, J.M.,
2018. Combining Benford’s Law and
Machine Learning to Detect Money Laundering. An Actual Spanish Court
Case. Forensic Science International, Volume 282, pp. 24–34
Bhattacharya,
S., Xu, D., Kumar, K., 2011. An ANN-Based Auditor Decision
Support System Using Benford's Law. Decision Support Systems, Volume
50(3), pp. 576–584
Bhosale,
S., Di Troia, F., 2022. Twitter Bots’ Detection
with Benford’s Law and Machine Learning. In Silicon Valley Cybersecurity Conference, pp. 38-54. Cham: Springer Nature Switzerland
Ergin,
E., Erturan, I.E., 2020. Is Benford’s Law Effective
in Fraud Detection for
Expense Cycle? Marmara Üniversitesi ?ktisadi ve ?dari Bilimler Dergisi, Volume 42(2), pp.
316–326
Fernandes, P., Antunes, M., 2023. Benford's Law Applied to Digital Forensic
Analysis. Forensic Science International:
Digital Investigation, Volume 45, p. 301515
Leonov,
P.Y., Suyts, V.P., Norkina, A.N., Sushkov,
V.M., 2022. Integrated Application
of Benford's Law Tests to Detect Corporate Fraud. Procedia Computer Science, Volume 213, pp. 332–337
Leonov,
P.Y., Suyts, V.P., Rychkov, V.A., Ezhova, A.A., Sushkov, V.M., Kuznetsova, N.V., 2021, September. Possibility
of Benford’s Law Application for Diagnosing Inaccuracy of Financial Statements.
In: Biologically
Inspired Cognitive Architectures Meeting, pp.
243–248, Cham: Springer International Publishing
Manuel,
P., García, C., 2021. Applicability of Benford’s Law to Fraud Detection. Universidad y Sociedad,
Volume 13(4), pp. 461–467
Nigrini,
M.J., 1993. The Detection of Income Tax Evasion Through an Analysis of Digital Distributions. University of Cincinnati,
USA
Nigrini,
M.J., 2012. Benford's Law: Applications for Forensic Accounting, Auditing, and Fraud Detection. John Wiley &
Sons, USA
Pupokusumo,
A.W, Handoko, B.L., Hendra, W., Hendra, R., Hendra, E., 2022. Benford’s Law as a Tool in Detecting Financial Statement
Fraud. Journal of Theoretical and Applied
Information Technology, Volume 100(14), pp. 5300–5305
Rad,
M., Amiri, A., Ranjbar, M.H., Salari,
H., 2021. Predictability of Financial Statements Fraud-Risk Using Benford’s
Law. Cogent Economics & Finance,
Volume 9(1), p. 1889756
