Structural Equation Modeling of Right-Turn Motorists at Unsignalized Intersections: Road Safety Perspectives
Corresponding email: azlan.abdaziz@mmu.edu.my
Published at : 31 Oct 2023
Volume : IJtech
Vol 14, No 6 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i6.6644
Mustakim, F., Aziz, A.A., Mahmud, A., Jamian, S., Hamzah, N.A.A., Aziz, N.H.B.A., 2023. Structural Equation Modeling of Right-Turn Motorists at Unsignalized Intersections: Road Safety Perspectives. International Journal of Technology. Volume 14(6), pp. 1216-1227
| Fajaruddin Mustakim | Faculty of Engineering and Technology, Malaysia Multimedia Uni., 75450 Ayer Keroh, Melaka |
| Azlan Abdul Aziz | Faculty of Engineering and Technology, Malaysia Multimedia Uni., 75450 Ayer Keroh, Melaka |
| Azwan Mahmud | Faculty of Engineering, Malaysia Multimedia Uni., 63100 Cyberjaya, Selangor |
| Saifulnizan Jamian | Faculty of Mechanical and Manufacturing Eng., Univ. Tun Hussein Onn Malaysia, 86400 Batu Pahat, Johor |
| Nur Asyiqin Amir Hamzah | Faculty of Engineering and Technology, Malaysia Multimedia Uni., 75450 Ayer Keroh, Melaka |
| Nor Hidayati Binti Abdul Aziz | Faculty of Engineering and Technology, Malaysia Multimedia Uni., 75450 Ayer Keroh, Melaka |
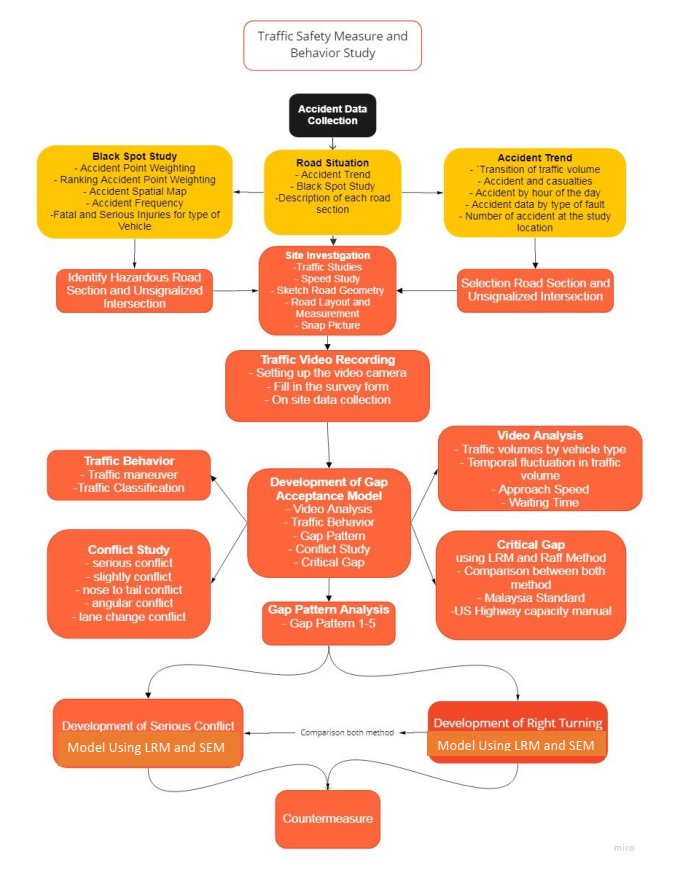
This study aims to determine traffic behavior at the selected unsignalized intersection
and the development of right-turn motorists (RTM) by adopting the logistic
regression method (LRM) and structural equation modelling (SEM). In the early
stage of the study, we analyzed the traffic behavior focusing on traffic volume
and turning volume at the field site. This study involves five unsignalized
intersections (UI), and it observes three types of turning volume: right turn
volume (RTV) from a minor road onto a major road, left turn volume (LTV) from a
minor road onto a major road, and right turn volume (RTV) from a major road
onto a minor road. Although the SEM approach is among the popular scientific
analysis and wisely applied in various fields of study, there is less attention
to traffic behavior and road safety. An SEM model was developed for right-turn
motorists using 812 datasets was developed, and variables that influenced the
decision of right-turn motorists (RTM) were identified. Among the six variables
analyzed in this statistical model, we identified gap, motorcycle rider,
conflict lane change, and the traffic signal to be significant.
Logistic regression method; Structural equation modeling; Traffic behavior
Trafic safety and management has attracted many
researchers to conduct various studies and analysis for improved safety and
efficiency (Trapsilawati et
al., 2023; Siregar et al., 2022; Sumaryo et al., 2019). Unsignalized intersections play
a crucial role in the transportation network, and understanding the traffic
flow and behavior at these intersections is essential for effective traffic
management and planning. Among the various movements at these intersections,
right turns pose unique challenges and safety concerns. Understanding the
factors that influence the behavior of right-turn motorists is essential for
developing effective road safety strategies. Researchers have developed many
methods to address this issue in decades, and one popular method is based on
statistical methods.
Another popular approach is Structural Equation Modelling (SEM), which is also a statistical method used to model complex relationships between observed and unobserved (latent) variables. SEM is interpreted as a multiple regression equation, estimating a group of datasets interdependently and simultaneously by using a structural model (Hair et al., 2006). Equation 1, defines the relationship between an observed and unobserved variable:
2.1. SEM Fit Index
SEM
programming comprises standard error with each calculated loading and related
t-test. If the sample size for SEM estimation is larger than 200, the
Chi-square value can also be determined, which usually results in high
statistical power. Therefore, significant loading is desirable, and even if it
is not attained, the model is still meaningful. Typically, the chi-square
(/df) statistical ratio recommended ranges as low as 2.0 and up to 5.0 (Tabachnick, Fidell, and Ullman, 2007). The root-mean-square error of
approximation (RMSEA) is used as the second fit index in this study. It
provides information about how well the model fits the data, considering the
number of parameters estimated in the model. If the model provides a good fit
to the population covariance matrix, it suggests that the model accurately
represents the relationships between the variables in the population. The
cut-off values of the RMSEA should be between 0 to 0.08 (McQuitty, 2004).
Besides the Chi-Square test, the Goodness of Fit Index (GFI) can be used to
measure the quantity of variance in the model by the estimated amount of
covariance (Tabachnick,
Fidell, and Ullman, 2007). This
statistical index ranges from 0 to 1. Adjusted Goodness of Fit Index (AGFI) is
a modification of the Goodness of Fit Index (GFI) that considers the degrees of
freedom in the model. AGFI is calculated by adjusting GFI for the expected fit
under the null hypothesis of a completely saturated model, given the degrees of
freedom in the actual model. Like the GFI, the AGFI ranges between 0 and 1, and
a value of 0.90 or higher shows a well-fitting model, according to (Tabachnick, Fidell, and Ullman, 2007).
The root mean square residual (RMR) is a
measure of the discrepancy between the hypothesized covariance model and the
sample residuals of the covariance matrix, and its scale depends on the
variables being measured. The Norm Fit Index (NFI) compares the value of the
model with the
value of the null model, which assumes that all tested
variables are unrelated and represents the worst-case scenario. This
statistical index ranges from 0 to 1. Another interesting model is called the comparative fit index (CFI).
It is a reviewed form of the NFI, which concentrates on sample size. The index performs well even though
the sample size is smaller (Tabachnick, Fidell, and Ullman, 2007). Like NFI, the value of CFI
ranges between 0 and 1. An index value that is close to 1 shows a good fit.
Too many models' fit indexes in SEM
create phenomena of reporting results because of complexity, issues, and the
acceptable margin of the fit indexes. Describing and evaluating a hypothesized
model does not require all fit indices to be included. The choice of the fit
index to use typically depends on the purpose of the study, as noted by Alavi et al.
(2020).
2.2. Model
Modification and Fitness
Although SEM
involves complex statistical methods, there are software tools available that
make it relatively easy to apply. The scientific tool can analyze single and
multiple models concurrently and estimate effectively. Modification indices
(MI) found under analysis properties in the SEM provide information on
modification value. Modifying covariances between variables, whether by
expanding the network or removing errors in the measurement model (MI), could
enhance the fit of models, including Chi-Square, NFI, RMSEA, RMR, GFI, AGFI,
RFI, IFI, CFI, and RMSEA (Arbuckle, 2013; McQuitty and Wolf, 2013; Loehlin,
2004). When attempting
to improve the model fit of an SEM, it is important to consider both the
theoretical aspects of the model and the fit indices. We should not disregard
theoretical considerations in favor of only improving the model fit (Teo, Tsai,
and Yang, 2013). Before
implementing the model in SEM, this study used the logistic regression method
to examine and validate all model parameters carefully to ensure that they
align with the theoretical foundation of the model.
2.3. Data
Collection
We performed this study on Malaysia's Federal Route
50. It has four lanes of a two-way, partially divided road. The total stretch
of the roadway from Batu Pahat to Ayer Hitam is about 40 km. The existing road
consists of high-density of access roads or unsignalized intersections. This is
because the location of the route crosses several housing areas, industrial
hubs, and commercial buildings. In the year 2022, it has a capacity providing
approximately 80,102 veh/day and up to 7,949 veh/hr. The design speed for this
route is around 100 kph. Meanwhile, the method applied in this study includes
site investigation, video recording, traffic behaviour analysis, critical gap,
speed study, gap pattern, development of right turn model, and the conflict
model. We have implemented binary regression or logistic regression and
structural equation modeling in the models.
Figure 1
Right turning at a three-leg unsignalized intersection, the four potential gap
patterns for motor vehicle acceptance or rejection (UI)
2.4. Traffic
Volume
We
collected a traffic count at five unsignalized intersections, UI 2, UI 9, UI
10, UI 8, and UI 20, using video cameras. Traffic data conducted in this paper
were based on hourly traffic volume and focused on three peak hours, namely
morning (8:00-10:00), midday (12:00-14:00), and afternoon (16:00-18:00). Figure
2 illustrates the highest traffic volume was during the afternoon at
(17:00-18:00) stated 4,804 veh/hr, 4,500 veh/hr, 4,368 veh/hr, 4,142 veh/hr and
2218 veh/hr for UI 2, UI 8, UI 9, UI20 and UI 10 respectively. The second
highest traffic volume was during the morning (8:00-9:00) recorded at 3,887
veh/hr, 3,632 veh/hr, 3,072 veh/hr, 2,760 veh/hr, and 2,707 veh/hr for UI8,
UI2, UI 10, UI20 and UI9 respectively. Conscience, the third highest traffic
volume was during midday at (13:00-14:00) got 3,628veh/hr, 3,612 veh/hr, 2,822
veh/hr, 2,551 veh/hr and 2,168 veh/hr for UI 20, UI 2, UI 8, UI 9 and UI 10,
respectively. Although UI 2 achieved the highest traffic volume during
(17:00-18:00= 4804 veh/hr, however in right turning volume from a minor road
onto a major UI2 received the lowest (17:00-18:00= 34veh/hr).
2.5. Right Turn
Volume from Minor Road
Right turning volume in this section is defined as right turn motorist from a minor road onto a major road at the selected intersection (Figure 2). Five unsignalized intersections (UI) were involved in right turn volume analysis, which are UI 2, UI 8, UI 9, UI 10, and UI 20. As mentioned before in the previous section, the traffic count was based on hourly traffic turning volume (veh/hr) at three peak hours (8:00-10:00), (12:00-14:00) and (16:00-18:00). Figure 3 shows turning volume over six hours' duration. Right turning flow at UI 10 recorded in uniform trend in early stage recorded (8:00-9:00 = 41 veh/hr), (9:00-10:00 = 39 veh/hr), (12:00-13:00 = 44 veh/hr), (13:00-14:00 = 55 veh/hr), (16:00-17:00 = 42 veh/hr) but drastically increase at (17:00-18:00 = 244 veh/hr). Other turning flows at UI 2, UI 8, UI 9, and UI 20 represent a stable turning maneuver and less fluctuation with a minimum range of 34 veh/hr and a maximum of 92 veh/hr, compared with UI 10.
Figure
2 Traffic volume from minor road fluctuation over six
hours survey during a typical weekday
Figure
3 Right turning volume from minor road fluctuation over
six hours survey during a typical weekday
2.6. Left Turning Volume from Minor Road
Left turning volume in this section is defined as a left turn motorist from a minor road onto a major road at the selected intersection. Figure 4 shows the turning volume over six hours' duration. Left turning volume at UI 9 recorded in less fluctuation trend in morning and midday, was (8:00-9:00 = 89 veh/hr), (9:00-10:00 = 65 veh/hr), (12:00-13:00 = 78 veh/hr), (13:00-14:00 = 67 veh/hr), (16:00-17:00 = 97 veh/hr) however sharply rise during the afternoon (17:00-18:00 = 213 veh/hr). Meanwhile, UI 10 has a different situation pattern during midday (12:00-13:00 = 115veh/hr), achieving the highest left-turning volume and second highest during the afternoon (17:00-18:00= 184 veh/hr). Subsequently, other turning volumes at UI 2, UI 8, and UI 20 represent a uniform turning maneuver and less fluctuation with a minimum range of 8 veh/hr and a maximum of 63 veh/hr.
Figure
4 Left turning volume from minor road fluctuation over six
hours survey during a typical weekday
2.7. Right Turn Volume from Major
Road (RTVmr)
Right turning volume from a major
road in this section is defined as the right turn motorist from a major road
onto a minor road at the selected intersection. Figure 5 shows the turning
volume over six hours' duration. Right turn volume from the major road has a
different turning pattern compared with other right turning volumes from the
minor road (Figure 3) and left turning volume from the minor road (Figure 4).
Concisely, the right turning volume at UI 8 in the morning was (8:00-9:00 = 70
veh/hr) and the number of traffic plumped (9:00-10:00 = 40 veh/hr). Meanwhile,
the volume rises drastically at 121 veh/hr and 123 veh/hr during midday
(12:00-13:00) and (13:00-14:00) respectively. However, the volume dropped
suddenly with 46 veh/hr in the afternoon (16:00-17:00) and increase doubled to
83 veh/hr at (17:00-18:00). Briefly, UI 20 demonstrate active variation volume
flow from morning stated (8:00-9:00 = 46 veh/hr) drop at (9:00-10:00 = 26
veh/hr) sharply rise in midday (12:00-13:00 = 58 veh/hr) and (13:00-14:00 = 95
veh/hr), slightly reduce in the afternoon (16:00-17:00 = 86 veh/hr) before
rocketed (17:00-18:00 = 111 veh/hr).
Figure 5
Right turning volume from major road fluctuation over six hours survey during a
typical weekday
Development of Logistic Regression
812 data points for Right-Turning
Motorists (RTM) comprised 351 accepted gaps, and 461 rejected gaps utilized in
the development of the RTM Models. Subsequently, gap, motorcycle rider,
conflict lane change (CLC), channelization, and traffic signal were set as
independent variables or predictors. Meanwhile, the dependent variable in
logistic regression was RTM and set to 1 and 0 if otherwise. Validation of the
model was done with SPSS Statistics 26. The significant intervals of 90%, 95%,
and 99% were determined using a stepwise selection procedure. The description
of all dependent and independent variables is explained in Table 1, and the RTM Models for Right Turn Motorists in Table
2.
Table 1 Attributes of traffic behavior
models
|
Abbr. |
Description |
|
RTM |
RTM=1 if the motorist turned right at a gap, but
0 if not. |
|
Gap |
Gap which is
rejected or accepted (sec). |
|
Car |
Car=1 if the RTM is a car, and 0 if otherwise. |
|
Mc |
Mc=1 if the RTM is a motorcycle, and 0 if
otherwise. |
|
Rider |
Rider= 1 if the RTM is rider, and 0 if otherwise. |
|
Van |
Van= 1 if the RTM is van, and 0 if otherwise. |
|
Lorry |
Lorry= 1 if the RTM is lorry, and 0 if otherwise. |
|
Bus |
Bus= 1 if the RTM is a bus, and 0 if otherwise. |
|
CLC |
Conflict lane change = 1 if CLC occurred and 0 if
otherwise. |
|
Gap1 |
If the gap was gap pattern 1 in Figure 4, Gap1=1,
but 0 if not. |
|
Gap2 |
If the gap was gap pattern 2 in Figure 4, Gap2=1,
but 0 if not. |
|
Gap3 |
If the gap was gap pattern 3 in Figure 4, Gap3=1,
but 0 if not. |
|
Gap4 |
If the gap was gap pattern 4 in Figure 4, Gap4=1,
but 0 if not. |
|
Gap5 |
If the gap was gap pattern 5 in Figure 5, Gap5=1,
but 0 if not. |
|
Chanlz |
If the channelization facility is in an
unsignalized intersection, so Chanlz = 1, but 0 if not. |
|
TSignal |
If all vehicles are in an unsignalized
intersection, so TSignal=1, but 0 if not. |
In
Model 1, three variable, which is vehicle gap, conflict lane change (CLC), and
traffic signal, achieved significance at a 99% level, followed by rider
received 95% significance, and channelization stated a 90% significance level.
Table 2 Logistic
Regression Models for Right Turn Motorists (RTMs)
|
Attributes |
Model 1 |
|
All (detail) | |
|
Constant |
-5.35(187.29)*** |
|
Gap |
0.96(201.97)*** |
|
CLC |
4.18(28.95)*** |
|
Rider |
0.59(5.73)** |
|
TSignal |
-0.67(6.36)*** |
|
Chanlz |
-0.83(3.04)* |
|
N |
812 |
|
NagelkerkeR2 |
0.72 |
|
H.R-Right Turn |
83% |
|
H.R-Total |
87% |
*,**,***=Significant at 90%,95%, and 99%
levels, respectively
The
dataset applied in the right-turning motorist (RTM) behavior model for logistic
regression is the same dataset implemented in structural equation modeling. The
relationship between exogenous and endogenous latent variables can be
visualized through the SEM diagram. In addition, SEM's ability to assess both
causal impact among these observed and unobserved variables. In this model,
endogenous variables were RTM and six exogenous variables (rider, gap, conflict
lane change, channelization, and traffic signal).
The
IBM SPSS AMOS 23 computer programming is used to develop structural equation
modeling (SEM). AMOS 23 (Arbuckle, 2013), is a
software for analyzing, validating, and testing observed data. Meanwhile, SPSS
26 is used to prepare the dataset. Table 3 shows the outcome results for each
variable in the analysis.
Table 3 Result of
SEM for Traffic Behaviour
|
Estimate |
S.E. |
C.R. |
P |
Label | |||
|
RTM |
<--- |
CLC |
.573 |
.063 |
9.168 |
*** |
par_5 |
|
RTM |
<--- |
Gap |
.080 |
.003 |
25.540 |
*** |
par_6 |
|
RTM |
<--- |
Tsignal |
-.080 |
.029 |
-2.764 |
*** |
par_7 |
|
RTM |
<--- |
Chlzation |
-.041 |
.045 |
-.926 |
.354 |
par_10 |
|
RTM |
<--- |
Rider |
.066 |
.028 |
2.394 |
.017 |
par_11 |
*,**,***=Significant
at 90%,95%, and 99% levels, respectively
The
details, such as parameter estimate, standard error (S. E), critical ratio (C.
R), and level of statistical significance (P), are described in Table 3. All
four variables, namely gap acceptance (Gap), traffic signal (TSignal), and
conflict lane change (CLC), were highly statistically significant statistically
at 99%, excluding motorcycle riders got a 95% significance level. Meanwhile,
channelization was found insignificant. Each parameter shows a positive sign,
except traffic signal and channelization get a negative sign. The positive sign
of conflict lane change, gap, and motorcycle rider shows RTM is likely to
accept a short gap. Subsequently, the negative sign of the traffic signal shows
the RTM is likely to accept a longer gap. The Chi-square ?2 was 9.445.
Meanwhile, the ?2/df statistic index was 3.145, which is less than 5.0, showing
a good fit of the model (Schumacker and Lomax, 2004). The root
mean square residual (RMR) index has a value of 0.010. The index of (RMR) less
than 0.08 means the index is quite good (Benitez et al., 2020).
Subsequently, the root mean squared error of approximation (RMSEA) is 0.05,
which is less than 0.05. A value equal to or less than 0.05 usually shows the
good quality of the model, and when RMSEA is between 0.07-0.09, the model is in
categories of logical estimation. (Khassawneh, Mohammad, and Ben-Abdallah, 2022). The goodness-of-fit index (GFI)
and the adjusted goodness-of-fit index (AGFI) had values of 0.996 and 0.973,
respectively. The index was close to 1.0, showing a perfect fit for the
conflict model (Hair et al., 2010). The
comparative fit index (CFI), tucker-lewis coefficient (TLI), and normal fit
index (NFI) were 0.996, 0.949, and 0.985, respectively. All Incremental Fit
Indexes are close to 1.0, representing the best fit of the model (Benitez, Ray, and Henseler, 2018). We
concluded that the fit of our model is excellent and sufficient to proceed. The
summary of the model index value and its requirement is shown in Table 4.
Table 4
Goodness-of-fit indexes
|
Indexes
Values |
Values |
Requirement |
|
Chi-Square ?2/df Goodness
of Fit Index (GFI) Adjusted
Goodness of Fit Index (AGFI) Comparative
Fit Index (CFI) Tucker-Lewis
Coefficient Index (TLI) Normal
Fit Index (NFI) Relative
Fit Index (RFI) Incremental
Fix Index (IFI) Root
Mean square Residual (RMR) Root
Mean Square Error of Approximation (RMSEA) |
9.45 3.15 0.99 0.97 0.99 0.95 0.99 0.93 0.99 0.01 0.05 |
Significance
> 0.05 Between
2-5 (Tabachnick,
Fidell, and Ullman, 2007) close
to 1, (Hair
et al., 2010) close
to 1, (Hair
et al., 2010) >
0.90, (Benitez,
Ray, and Henseler, 2018) >
0.90, (Benitez,
Ray, and Henseler, 2018) >
0.90, (Benitez,
Ray, and Henseler, 2018) >
0.90, (Benitez,
Ray, and Henseler, 2018) >
0.90, (Benitez,
Ray, and Henseler, 2018) <
0.08 (Benitez
et al., 2020) <
0.08 (Khassawneh,
Mohammad, and Ben-Abdallah, 2022) |
The root mean squared error of the approximation calculation formula is defined by Equation 2.
Where
N number of observations (812), df the degrees of freedom (3), and Chi-square of the
model (9.45).
At
the early stages, using SEM can be challenging as researchers need a basic
understanding of statistical analysis, model fit indices, variable networks,
and the connections between endogenous and exogenous variables, as well as
observed and unobserved (latent) quantitative variables. However, as one gains
experience and regularly practices developing structural models with proper
guidance, it becomes more engaging. This is especially true when leveraging
modification indices (MI) to fine-tune the model, such as increasing covariance
between independent variables based on MI suggestions, leading to improved
model fit indices.
The
resulting outcome from both scientific methods (SEM and LRM) revealed
similarity independent variables such as gap, traffic signal and conflict lane
change, acquiring a significance level at 99%. Only the RTM motorcycle achieved
a 95% confidence level. The same -/+ sign of each variable is given in both
methods. Despite the independent variable of channelization insignificance in
structural equation modeling, these parameters have statistical significance at
90% in the logistic regression model. All ten goodness-of-fit indices support
the analysis having more accuracy in the SEM. SEM can present a visualization
modeling network. Meanwhile, LRM has the advantage of assisting in explaining the result and early preparation of
selection variables in the model before execution of the SEM. Thus, a
combination of both scientific and statistical might complement each other and
create essential understanding in our research work. The results of the SEM
analysis provide a comprehensive understanding of the behavior of right-turn
motorists at unsignalized intersections from a road safety perspective.
The study identifies significant variables that influence
the decision-making process, highlighting their impact on road safety
considerations. These findings contribute to the development of effective road
safety measures and interventions for unsignalized intersections. Furthermore,
the findings could serve as basic research for road safety design, autonomous
vehicle as well as vehicle-to-vehicle communication, specifically employing
artificial intelligence methods. Besides that, this study has the potential to extend another three-turning behavior at
unsignalized intersections, such as a left turn from a minor road to a major
road, a right turn from a major road to a minor road, and a left turn from a
major road to minor road. Moreover, the researcher has intention to explore the
Internet of Vehicle (IoV), vehicle-to-vehicle communication (V2V),
vehicle-to-infrastructure (V2I), and vehicle-to-everything (V2X) in traffic
behavior study for the next future research work. Future studies may address
issues in information sharing in the heterogenous vehicular networks about
traffic conditions such as traffic congestion, accidents with each other and
with traffic controller systems. This will enable more efficient traffic flow
and fully autonomous vehicles.
This work was supported by the Ministry of Higher
Education, Malaysia FRGS/1/2019/TK08/MMU/03/1 and TMRND Grant MMUE/190012.
Alavi, M., Visentin, D.C., Thapa, D.K., Hunt, G.E., Watson R., Cleary, M., 2020. Chi-Square for Model Fit in Confirmatory Factor Analysis. Journal Advance Nursing, Volume 76(9), pp. 2209–2211
Arbuckle, J.L., 2013. Amos 22 User Guide. USA: Amos Development Corporation
Benitez, J., Henseler,
J., Castillo, A., Schuberth, F., 2020. How To Perform And Report An Impactful Analysis Using Partial
Least Squares: Guidelines for Confirmatory and Explanatory IS Research. Information and Management, Volume 57, p. 103168
Benitez, J., Ray, G., Henseler, J., 2018. Impact of Information Technology Infrastructure Flexibility on Mergers and Acquisitions. MIS Quarterly: Management Information Systems, Volume 42(1), pp. 25–43
Branzi, V., Meocci, M.,
Domenichini, L., Calcinai, M., 2021. A Combined Simulation Approach to Evaluate
Overtaking Behaviour on Two-Lane Two-Way Rural Roads. Journal of Advanced
Transportation, Volume 2021, pp. 1–18
Fajaruddin, M., Aziz, A.A., Fujita, M., Wisetjindawat, W., Ahmad, M.N., Sukor, N.S.A., 2021. An Analysis of Right-Turning
Vehicles and Gap Acceptance Behaviour Models on Malaysian Rural Roads. International
Journal of Road Safety, Volume 2(1), pp. 45–53
Fajaruddin, M.,
Fujita, M., Wisetjindawat, W., 2013. Analysis of Fatal-Serious Accidents and Dangerous Vehicle Movements at Access Points on Malaysian Rural Federal Roads. Journal of Japan Society of Civil Engineers, Volume 69(4), pp. 286–299
Gharraie, I., Sacchi, E., 2021. Severity Analysis of Wildlife–Vehicle Crashes Using Generalized
Structural Equation Modeling. Transportation Research Record, Volume 2675(2), pp. 53–64
Grace, J.B., Schoolmaster, D.R.Jr., Guntenspergen, G.R., Little, A.M., Mitchell, B.R., Miller, K.M., Schweiger, E.W., 2012. Guidelines for a Graph-Theoretic Implementation of Structural Equation Modeling. Ecosphere, Volume 3(8), pp. 1–44.
Hair, J.F., Black, W.C., Babin, B.J., Anderson, R.E., 2010. Multivariate Data Analysis. 7th Edition. Englewood Cliffs: Prentice Hall
Hair, J.F., Jr., Black, W.C., Babin, B.J., Anderson, R.E., Tatham, R.L., 2006. Multivariate Data Analysis. 6th Edition. Upper Saddle River, NJ: Prentice-Hall
Hyun, K.K., Mitra, S.K., Jeong, K., Tok, A., 2021.
Understanding The Effects of Vehicle Platoons on Crash Type and Severity. Accident
Analysis & Prevention, Volume 149, p. 105858.
Khassawneh, O.,
Mohammad, T., Ben-Abdallah, R., 2022. The Impact of Leadership on Boosting
Employee Creativity: The Role of Knowledge Sharing as a Mediator. Administrative Sciences, Volume 12(4), p. 175
Kim, K., Pant, P., Yamashita, E., 2011. Measuring Influence of Accessibility On Accident Severity With
Structural Equation Modeling. Transportation Research Record, Volume 2236(1), pp. 1–10
Lee, J-Y, Chung, J-H, Son, B., 2008. Analysis of
Traffic Accident Size for Korean Highway Using Structural Equation Models. Accident
Analysis & Prevention, Volume 40(6), pp. 1955–1963
Loehlin, J.C., 2004. Latent Variable Models: An Introduction to Factor, Path, and Structural
Equation Analysis. 4th Edition. London: Lawrence Erlbaum Associates
McQuitty, S., 2004. Statistical
Power and Structural Equation Models in Business Research. Journal of
Business Research,
Volume
57 (2), pp. 175–183
McQuitty, S., Wolf, M., 2013. Structural Equation Modeling: A Practical
Introduction. Journal of African Business, Volume
14(1), pp. 58–69
Schumacker, R.E., Lomax, R.G., 2004. A
Beginner's Guide to Structural Equation Modeling. 2nd Edition. London: Lawrence
Erlbaum Associates, Inc
Sevenster, A., Farah, H., Abbink,
D., Zgonnikov, A., 2023. Response Times In Drivers’ Gap Acceptance Decisions
During Overtaking. Transportation Research Part F: Transportation Research Part F: Psychology
and Behaviour. Volume 94, pp. 329–340
Siregar, M.L., Tjahjono, Yusuf, N., 2022.
Predicting the Segment-Based Effects of Heterogeneous Traffic and Road
Geometric Features on Fatal Accidents. International Journal of
Technology, Volume 13(1), pp. 92–102
Sumaryo, S., Halim, A., Ramli, K., Joelianto, E.,
2019. A Model for Accelerating Discharge of Lane Traffic to Facilitate
Intersection Access by EVs. International Journal of Technology, Volume 10(1), pp. 116–125
Tabachnick, B.G., Fidell, L.S., Ullman, J.B., 2007, Using Multivariate Statistics. 5th Edition. New York: Allyn and Bacon
Teo, T., Tsai, L.T., Yang, C.-C., 2013. Applying Structural Equation Modeling (SEM) in Educational
Research: An Introduction. In: Application of Structural Equation Modelling in
Educational Research and Practice, Khine,
M.S., (ed.), Rotterdam/ Boston / Taipei: Sense
Publishers
Trapsilawati, F., Li, F., Yisi, L., 2023.
Ergonomics Considerations in Air Traffic Conflict Detection and Resolution. International
Journal of Technology, Volume 14(4), pp. 898–910
Xu, C., Li, D., Li, Z., Wang, W., Liu, P., 2018.
Utilizing Structural Equation Modeling And Segmentation Analysis in Real-Time
Crash Risk Assessment on Freeways. KSCE Journal of Civil Engineering, Volume 22(7), pp. 2569–2577
Yang, D., Xie, K., Ozbay, K., Yang, H., 2021. Fusing Crash Data and Surrogate Safety Measures For Safety
Assessment: Development of a Structural Equation Model
With Conditional Autoregressive Spatial Effect and Random Parameters. Accident Analysis & Prevention, Volume 152, p. 105971
Zgonnikov, A., Abbink, D., Markkula,
G., 2022. Should I Stay or Should I Go? Cognitive Modeling of Left-Turn Gap
Acceptance Decisions in Human Drivers. Human Factors. Volume 2022, p. 00187208221144561
