Design Optimization of a Point Absorber and Hydraulic Power Take-Off Unit for Wave Energy Converter

In recent times, the point absorber Wave Energy Converter (WEC) has gained popularity due to its practicality. Investigating the parameters of the Hydraulic Power Take-Off (HPTO) in the WEC, including hose diameter and check valve variations, is crucial. This study analyzes optimization using the Sequential Quadratic Programming (SQP) method in MATLAB/SimScape, leading to a more comprehensive understanding of the interactions among HPTO components, such as hydraulic cylinders, check valves, hoses, accumulators, motors, and generators. Key system performance indicators, including pressure drop, flow rate, and power output, were assessed in both single and two-point absorber HPTO configurations. The optimization process yielded a maximum hydraulic power output of 7.33 kW, a mechanical power output of 6.41 kW, and an electrical power output of 5.4 kW using a 2-inch hose diameter. Additionally, utilizing a two-point absorber model enhanced power generation capacity by 47.4%, reaching 9.45 kW. The findings highlight the significant pressure drop at the check valve, with the 2-inch hose model experiencing a drop of 31.874 bar. These results demonstrate that optimizing HPTO parameters can significantly improve the efficiency of converting wave energy into electricity, providing valuable design recommendations for WEC technology.

Design optimization; Hydraulic power take-off; Hose diameter; Sequential quadratic programming; Wave energy converter

The literature review highlights the significance of a robust Power-Take Off (PTO) system in efficiently converting ocean wave energy into electrical power (Jahangir, Alimohamadi, and Montazeri, 2023; Wang, Isberg, and Tedeschi, 2018; Drew, Plummer, and Sahinkaya, 2009). It specifically emphasizes the suitability of Hydraulic Power Take-Off (HPTO) systems due to their compatibility with high power-to-frequency ratios and low-frequency ocean environments. This assertion is supported by references such as (Veerabhadrappa et al., 2022; Jusoh et al., 2019; Gaspar et al., 2018; Hansen, Kramer, and Vidal, 2013; Marquis, Kramer, and Frigaard, 2010; Drew, Plummer, and Sahinkaya, 2009). Hydraulic systems are favored for their adaptability, and various configurations of HPTO systems are discussed, including Discrete Displacement HPTO (Penalba, Cortajarena, and Ringwood, 2017; Penalba et al., 2017; Penalba and Ringwood, 2016; Hansen, Kramer, and Vidal, 2013), Multi-point Absorber (Do, Dang, and Ahn, 2018; Hansen and Pedersen, 2016; Hansen, 2013), Double Acting Cylinder (Sotoodeh, 2022; Antolín-Urbaneja et al., 2015; Lin et al., 2015) and multi-chamber cylinder (Li et al., 2022). These systems, along with various parameter configurations (Jusoh et al., 2022; 2021), underscore hydraulic systems' versatility in WEC.

Furthermore, the review emphasizes the importance of evaluating the performance of valves and hoses, pivotal components in the HPTO setup, to understand fluid flow dynamics and pressure distribution within the system. However, it does not explicitly compare the performance or effectiveness of different types of valves and hoses, which could be a potential avenue in this research.

The necessity for a more efficient and economical approach to optimize HPTO systems for maximum power generation needs to be investigated. To advance WEC with HPTO, the stability and energy absorption mechanisms of the HPTO system need refinement. The optimal design of the kinematics of the floating arm cylinder plays a pivotal role in the HPTO system. It plays a pivotal role in achieving optimal power generation. Therefore, it is essential to accurately estimate each component, as mentioned in the study by (Waskito et al., 2024). However, determining parameter values for each HPTO component poses a challenge. Experimental methods for determining these parameters require distinct components with different specifications, entailing significant costs.

        In this study, we employ the Sequential Quadratic Programming (SQP) numerical optimization method to estimate parameter values for each component of the Hydraulic Power Take-Off (HPTO) system, specifically focusing on the check valve and hose. Unlike traditional experimental methods, SQP offers advantages such as handling nonlinear relationships, constrained optimization, smooth and continuous functions, iterative refinement, handling multiple design variables, global convergence, and incorporation of sensitivity analysis. By leveraging SQP, the study aims to identify parameter combinations that maximize power output and consider existing constraints effectively and economically. This systematic approach represents a novel method for optimizing HPTO systems in WECs, thereby addressing the research gap and contributing to the advancement of wave energy conversion technologies.

This section describes the methods for modeling the floating absorbers and HPTO. It begins by modeling the WEC with the HPTO unit, providing a mechanical overview of the WEC. Next, it describes the mathematical formulation of the HPTO and the parameter optimization process using Sequential Quadratic Programming.

2.1. Modeling the WEC with HPTO Unit: An Overview
        The evaluation and presentation of the HPTO is initiated by outlining its layout and key components. This includes a description of the HPTO's main features and overall operation. The HPTO with Double Acting Cylinder (DAC) was selected based on its component efficiency and power generation capabilities. In this system, the floating absorber is connected to a fixed body to capture the kinetic energy of ocean waves effectively. 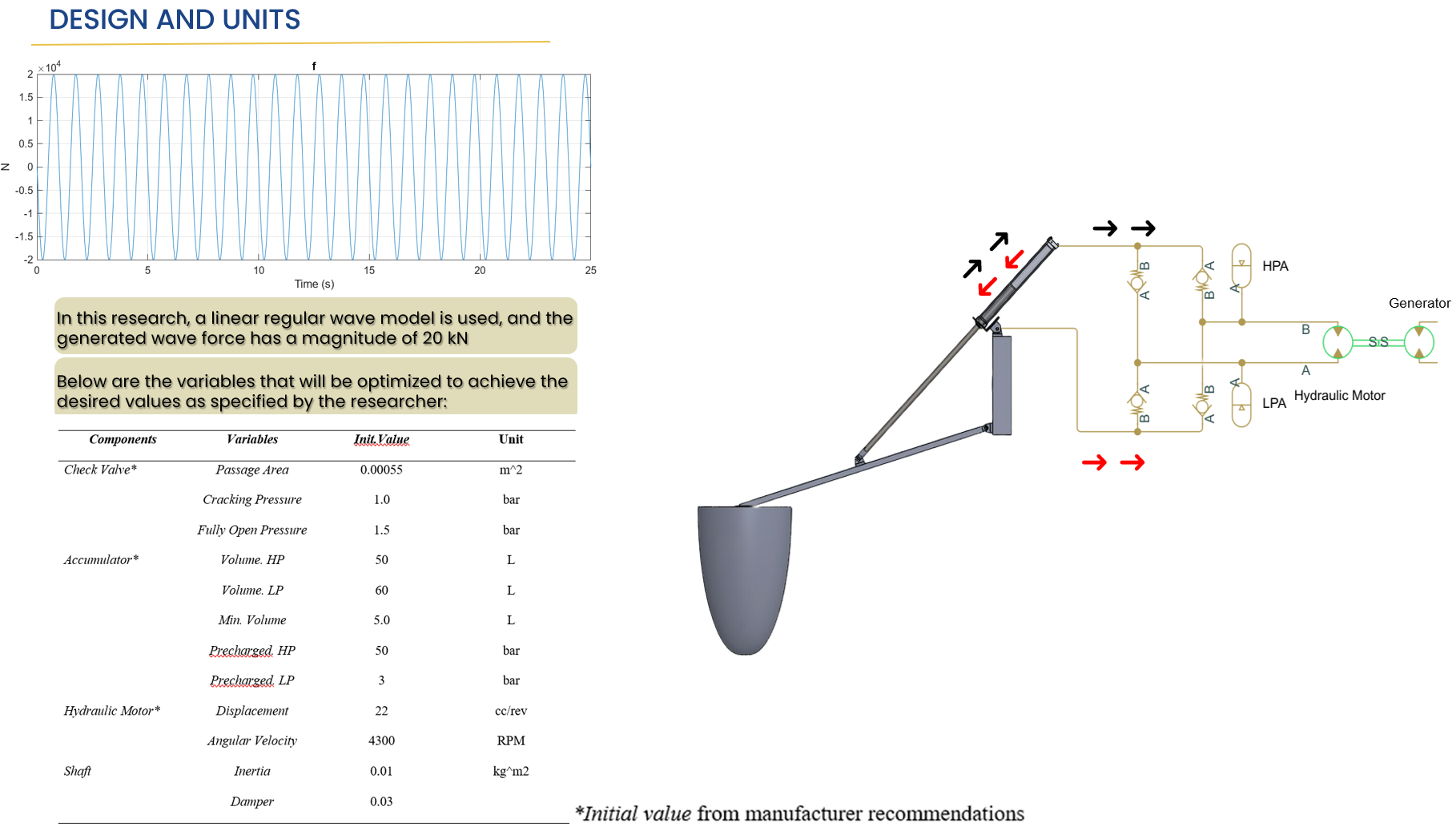The HPTO system is coupled with floating absorbers to convert mechanical energy into usable electrical power. Figure 2 displays the floating absorber system with a Hydraulic Power Take-Off unit. This unit comprises a Hydraulic Motor (HM), Check Valve (CV), High-Pressure Accumulator (HPA), Low-Pressure Accumulator (LPA), and a generator (G). In this design, the floating absorber's arm experiences reciprocating motion in response to pitch and heave motions caused by ocean waves at certain frequencies. This arm motion actuates the cylinder mechanism, generating pressure in each chamber. This pressure drives hydraulic fluid into the HPA via hydraulic hoses and check valves (CV1 and CV3). The pressurized fluid is then directed to the HM. Any excess pressure from the hydraulic motor is stored in the LPA, subsequently re-entering the flowline input of the double-acting cylinder through CV2 and CV4.

Figure 1 Design and Modeling of the WEC, Single-Point WEC System, Adepted fron Waskito et al., (2024)

2.2. Mechanical overview of the WEC

      The geometry of the floaters can be represented as a combination of a sphere and an upper truncated cone. These floaters are primarily constructed with glass-fiber material and include a ballast chamber that can be filled through a hole located at the bottom. This chamber retains water during power generation. The ballast serves two main purposes: reducing the absorber's natural frequency and adjusting the draft of the floater as required. Additionally, the PTO cylinders serve as a mechanism for elevating the floaters during storm protection.

         The oscillating motion of the floater arm generates a moment, as depicted in Figure 3. The arm position is described by the angle  which is defined to be zero when the floater is horizontal. Positive rotation is defined as the floater moving upwards. The angular velocity of the arm is denoted  The PTO cylinder force is denoted  and the cylinder stroke  The length  is the cylinder stroke at which the arm angle  is zero. The distance  is the cylinder’s moment arm for applying torque to the float arm and is dependent on the angle  The relation of the cylinder stroke and arm angle may be expressed in Equations (1-3),

The cylinder’s moment arm  may be expressed as:

where J_WEC is the floater and arm moment of inertia of wave energy converter,  is the added mass.  are the angular acceleration, angular velocity, and angular position of WEC during the pitch motion.  is the radiation impulse response function,  is the time delay,  is the hydrostatic restoring coefficient,  is the impulse response function, and  is the undisturbed wave elevation at the floater center point. The coefficients can be determined from hydrodynamic analysis using potential flow computation such as the Constant Panel Method (CPM), Higher Order Boundary Method (HOBEM), and ANSYS AQWA (ANSYS 2014; Newman 1986) (11-12). In Equation (4) the non-linear effect of HPTO is considered, so that the moment on HPTO can use Equation (5). 

2.3. Mathematical formulation of the HPTO model

     In the HPTO unit, many parameters are considered, such as chamber piston area  piston friction  the pressure of the hydraulic chamber  piston acceleration  Mass of the piston, rod, and oil  and gravitational acceleration  All equations are written in Equation (6-8).

 The piston chamber experiences constantly changing pressure due to the upward and downward motion. By using equations (9) and (10), it is possible to obtain dynamic values of pressure in the piston chamber by considering the effective bulk modulus  in/out volumetric flow  and velocity on piston  The chamber area is obtained from Equations (11) and (12).  are the piston and rod diameters. 

The fluid flow rectifier uses four check valves in each cylinder. In equation (13),  is the flow through the check valve.  are the pressure on the in and out section of the valve.  is the discharge coefficient.  is the area of the valve.  is the density of fluid, oil.

     High-pressure accumulators (HPA) and Low-Pressure accumulators (LPA) are essential components in maintaining pressure stability in the PTO system. Equation (14-17) is used to find the pressure and volume values of the accumulator.  are the pressure and pre-charge pressure in the HPA and LPA.  are the initial and the instantaneous volume of gas in the HPA and LPA, and ? is the adiabatic index accumulators.

Volumetric flow in HPA and LPA can be calculated by equations (18) and (19):

Equation (20) below is used to obtain volumetric flow through the hydraulic motor.   are displacement, speed, and volumetric flow losses of the HM. The torque in the HM  can also be determined by Equation (21), where is the difference in pressure in HM.

Hoses play a crucial role in connecting different components in hydraulic systems. They facilitate the smooth flow of hydraulic fluid, which helps to convert fluid energy into mechanical energy. This process ultimately leads to the generation of electrical power. During simulations conducted in Simulink, hoses are represented as hydraulic resistive tubes, accounting for the hydraulic channel's resistance. Additionally, these hoses tend to experience pressure losses, that is subsequently simulated within Simulink using the Darcy equation as in the following Equations (22-24):

P is Pressure loss along the pipe due to friction, q is flowrate through the pipe. Re is a Reynold Number, and  are Reynold number at laminar and turbulent flow. K_s is the shape factor that characterizes the pipe cross-section.  are friction factors at laminar and turbulent flow.  are area, diameter, and length of pipe hydraulic. r is Height of the roughness on the pipe internal surface and, v is fluid kinematic viscosity.

2.4. Parameter Optimization of HPTO using Sequential Quadratic Programming

         Figure 3 shows the flow chart of HPTO optimization process. The initial value for finding the optimal parameters in the check valve, accumulator, hose, and hydraulic motor is determined by the predetermined sizing of the hydraulic cylinders and configurations of the components.

         The Hydraulic Power Take-Off (HPTO) design phase encompasses the establishment of layout, schematics, and configurations. This design process is executed using MATLAB/Simscape and Simulink software. An approach based on available manufacturer specifications is employed to determine initial component parameters, as outlined in Table 1. Simulations are conducted on the design of a single absorber to assess its performance, with simulation results compared against desired performance outputs. This iterative process involves random component selection until suitable outputs and parameters are approximatedSubsequently, these parameters are processed using the Sequential Quadratic Programming (SQP) algorithm through the Response Optimizer feature in order to optimize the HPTO design. This optimization aims to determine the most suitable parameter configurations obtained from Equation (25)


 is the gradient of the Lagrangian function,  is the gradient of the objective function  is the sum of all equality constraints,  is the sum of all inequality constraints. In this study, the wave model employed is that of a regular wave with a force amplitude of 20 kN and a wave frequency of 6.28 rad/s, as shown in Figure 4. This wave frequency represents a wavelength of 1.56 m, and with an absorber diameter of 0.2 m, it corresponds to  which is around resonance frequency. 

Figure 3 Flow chart of the HPTO optimization process

Figure 4 Regular sine wave force input at the hydraulic cylinder 20kN

The Response Optimizer in MATLAB software enables users to determine design parameters based on the system's response to the desired objectives. To achieve this, specific values need to be defined. This optimization aims to ensure that the motor speed does not exceed 4300 RPM or 460 rad/s. Figure 5 illustrates the angular motor speed amplitude in rad/s before optimization.