Design, Manufacture and Control of a Multi-layer Piezoelectric Actuator

Title: Design, Manufacture and Control of a Multi-layer Piezoelectric Actuator

Authors
Authors and Affiliations

Indrawanto, Indra Agung Ariwi Saputro, Vani Virdyawan, Tegoeh Tjahjowidodo

Corresponding email: indrawanto@itb.ac.id

Published at : 10 Jul 2024
Volume : IJtech Vol 15, No 4 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i4.6605

Cite this article as:
Indrawanto, Saputro, I.A.A., Virdyawan, V., Tjahjowidodo, T., 2024. Design, Manufacture and Control of a Multi-layer Piezoelectric Actuator. International Journal of Technology. Volume 15(4), pp. 1118-1132

Downloads

Indrawanto	Production Engineering Research Group, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Jl. Ganesa 10, Bandung 40132, Indonesia
Indra Agung Ariwi Saputro	Mechanical Engineering Study Program, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Jl. Ganesa 10, Bandung 40132, Indonesia
Vani Virdyawan	Production Engineering Research Group, Faculty of Mechanical and Aerospace Engineering, Institut Teknologi Bandung, Jl. Ganesa 10, Bandung 40132, Indonesia
Tegoeh Tjahjowidodo	KU Leuven, Department of Mechanical Engineering, Jan Pieter de Nayerlaan 5, 2860 Sint-Katelijne-Waver, Belgium

Email to Corresponding Author

Abstract

Design, Manufacture and Control of a Multi-layer Piezoelectric Actuator

A piezoelectric-based micro motion actuator is typically used in micro-scale movement technologies, with the actuator developed to deliver very small movements and high resolution for motion within several micrometer ranges. However, a significant challenge from the strong, nonlinear hysteresis arises affects the piezoelectric materials joining input voltage to output movement, which deteriorates the accuracy of the actuator and causes instability in a closed-loop system. To obtain high precision, accuracy and reduced nonlinear effects, piezoelectric actuators must be controlled with hysteresis compensation. Therefore, this research developed a piezoelectric-based microactuator system with a control scheme based on PID (proportional-integral-derivative) combined with the inverse hysteresis model implemented to compensate for the actuator's hysteresis. Furthermore, a Modified Prandtl-Ishlinskii (MPI) model was used to capture the hysteresis phenomenon, where its parameters were obtained through a system identification process. The inverse model of the hysteresis was then used to generate feedforward signals in the control system. The results showed that the control scheme is able to provide an accurate motion due to the decrease in hysteresis compensation signals from 4.87 to 0.97 . The closed loop control system consisting of the PID control and hysteresis compensation further improved the accuracy of the piezoelectric actuator and reduced the error down to 0.41 .

Keywords

Hysteresis; Micro motion actuators; Modified Prandtl-Ishlinskii model; PID control; Piezoelectric

Introduction

A micro motion actuator is a device capable of generating microscale movements at an accuracy of 0.001 mm, even extending to nanometres. This technology is widely applied in tools that require movement with exceptionally high precision and accuracy, such as micro robots (Karpelson, Wei, and Wood, 2012), atomic force microscopy (Leang and Devasia, 2006), laser beam alignment (Qin et al., 2020), ultra-precision machines (Tian, Zhang, and Shirinzadeh, 2011), etc.

Currently, the types of actuators used to achieve precise and accurate movements incorporate active or smart materials such as piezoelectric (Matsuda, Matsuo, and Ueyama, 2001), shape memory alloy (SMA) (Jani et al., 2014), voice coil motors (Zheng et al., 2018), and magnetostrictive substancese (Apicella et al, 2019). Piezoelectric actuators (PEA) are the most widely used due to certain significant features namely, high rigidity, rapid response, fine motion resolution, and large force capabilities (Cao and Chen, 2015). However, piezoelectricity has several disadvantages, and the most detrimental is the highly nonlinear hysteresis relationship between the input voltage and the output movement (Damjanovic, 2006; Rodriguez-Fortun et al., 2011; Heywang, Lubitz and Wersing, 2008). This characteristic disadvantage can lead to inaccuracies and instability, requiring dedicated controllers for compensation (Changhai and Lining, 2005). Therefore, the Prandtl-Ishlinskii (P-I) model was developed to address the inertial dependency at high frequencies (Hassani and Tjahjowidodo, 2011). An extensive survey of hysteresis mathematical models was carried out, presenting classical formalism and using it for the development of more comprehensive models and corresponding controllers (Hassani, Tjahjowidodo, and Do, 2014). Piezoelectricity is also used for energy harvesting, apart from the application in actuators and sensors (Akbar et al., 2022).

Several mechanisms have been developed to enable both planar and rotary motions using piezoelectric actuator. Devos et al., (2004), designed a planar piezo motor actuated by four piezoelectric motors arranged in a dedicated formation, enabling the delivery of linear motion in three-dimensional space. Li and Xu, (2009), proposed a parallel micromanipulator offering decoupled motion in 3DOF. Polit and Dong, (2011), designed a piezo-driven parallel kinematic nanopositioning planar mechanism enabling decoupled motions in two planar directions. Furthermore, Hassani and Tjahjowidodo (2013), proposed a 3-Degree of Freedom pyramidal-shaped piezo-driven mechanism capable of delivering planar motion in x–y, z–y and x–z planes. The mechanism operates in two modes, namely low and resonance frequencies for high precision positioning (stepping mode) and maximizing the speed (resonant mode), respectively.

In some applications, a direct piezo actuation is required, and a typical example is a micro-macro manipulator such as the one designed for in-vitro intracytoplasmic sperm injection (Fujii et al., 2020). Despite the relative simplicity, this mechanism faces a dual challenge, tend to suffer severely from the hysteresis property inherent in piezoelectricity.

This paper focused on a detailed design of a direct piezoelectric-based actuator system, with a feedback controller and model-based feedforward compensation to counteract the hysteresis phenomenon. The validation test results of the piezoelectric actuator, and the control law were presented through numerical simulations and experimental trials. In conclusion, it examined the main advantages of the developed actuator, with focus on the internally equipped position sensor, which significantly enhanced the performance.

The research was carried out in four phases shown in Figure 1, with the first focused on determining the specifications and design requirements of the actuator, taking into account certain limitations to ensure manufacturability with available materials. The actuator range of motion was set to a maximum of 50 and an error of less than 2 . Subsequently, the design comprising both mechanical and electrical components, were developed based on predetermined specifications. The actuator displacement was measured using a calibrated load cell, which evaluated the models in piezoelectric crystals with significant impact on accuracy at the micro-scale. The results obtained served as a basis for developing the hysteresis compensator model.

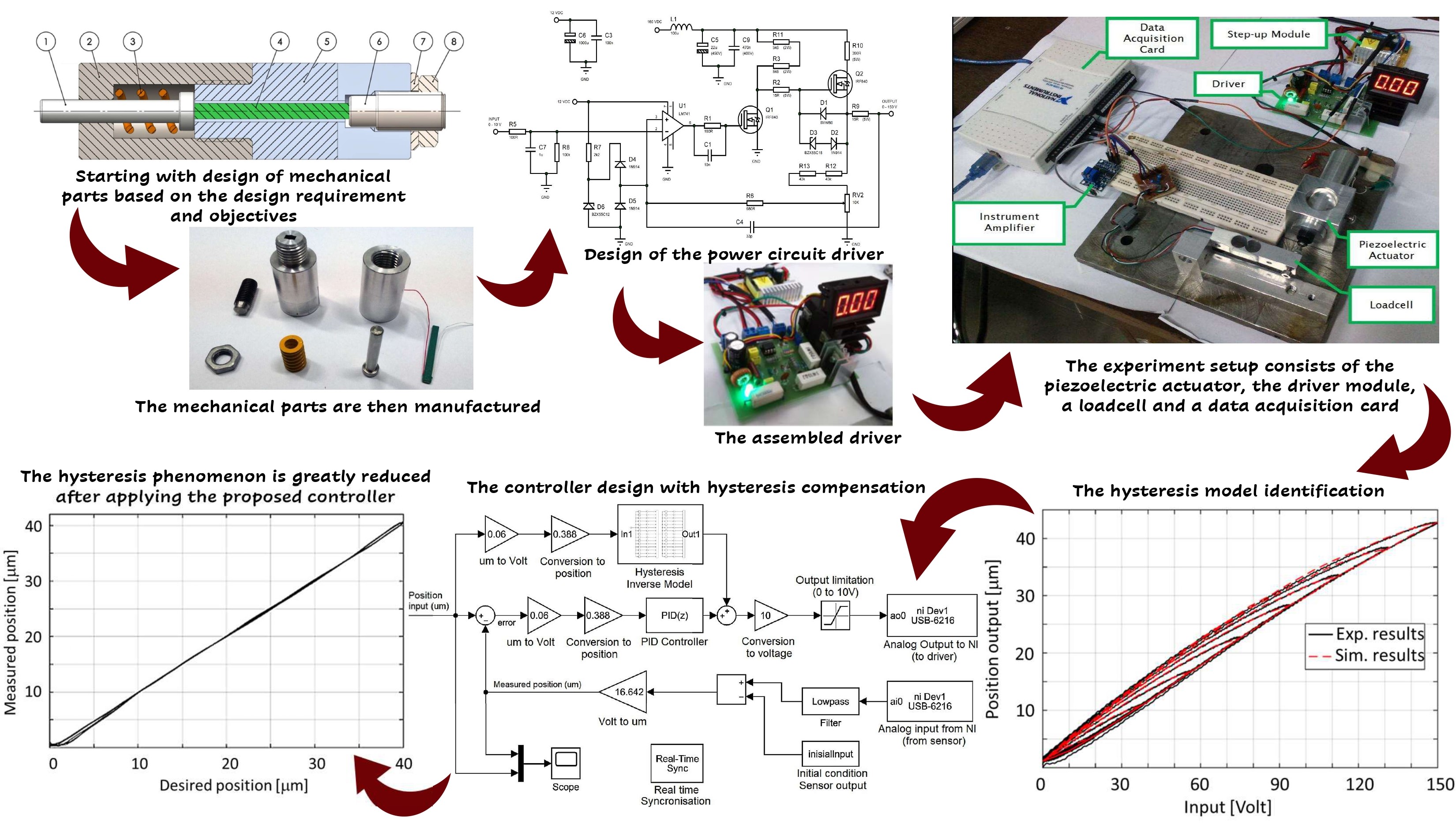
Figure 1 Phases in the development of the piezoelectric-based actuator system

The second phase focused on the manufacturing of the mechanical and electronical components, as well as designing the structure of the position control system, which integrated feedback and feedforward control strategies, using the hysteresis model examined in the first phase.

The third phase also known as the identification phase focused on distinguishing the dynamic parameters of the mechanical system, and hysteresis model, including testing the electronic circuit. The results obtained were then used to adjust and optimize the parameters of the feedback and feedforward control gains.

The fourth phase centered on testing the performance of the developed system, by using a reciprocating trajectory to investigate the effectiveness of the control system. In addition, this phase was completed by proving the satisfactory performance of the developed piezoelectric actuator system.

Experimental Methods

Hysteresis modelling was carried out to capture the characteristic behaviors of piezoelectric systems. In addition, through mathematical modeling, hysteresis can be accurately represented, enabling the development of compensatory strategies to reduce the effect. In this context, three hysteresis models, namely the Bouc-Wen, Prandtl-Ishlinskii (P-I) and Modified Prandtl-Ishlinskii(MPI), was discussed in the following sub-sections.

2.1. Bouc-Wen Model

The Bouc-Wen model was widely used to characterize hysteresis in piezoelectric systems. This model was expressed in a unified form as stated in Equations 1 and 2 (Lin and Yang, 2006; Gomis-Bellmunt et al, 2009; Zhu and Wang, 2012),

where y(t) is the output of the piezoelectric actuator displacement, m, b and k are mass, damping, and spring constant, respectively. In addition, u is the input voltage, d is the ratio of the linear force constant to the input voltage, and h is the force with hysteresis. The values of and n are shape factors tuned for the hysteresis model. One advantage of the Bouc-Wen model is that it uses only a few parameters however, the traditional one is only suitable for symmetrical hysteresis forms (Ha et al, 2006; Wang and Zhu, 2011).

1.2. Prandtl-Ishlinskii (P-I) Model

The Prandtl-Ishlinskii (P-I) model uses a combination of backlash operators to form a hysteresis profile, as shown in Figure 2. Despite the similarity to the Bouc-Wen model, the P-I model lacks the ability to capture asymmetric hysteresis.

Figure 2 Illustration of backlash, (a) backlash operator with weight/slope, (b) physical example of backlash in mechanical systems, (c) Simulink^® (MATLAB, 2023) model of Prandtl-Ishlinskii model (d) backlash operators.

The P-I model shown in Figures 2(a) and (b), included the backlash operator (play) as stated in Equation 3 (Xu and Li, 2010),

where is the input, is the output of the hysteresis model, is the threshold value or the width of the backlash, and is the sampling time. The initial conditions of Equation 3 are stated in Equation 4,

where

is the initial condition of the output, in addition the backlash operator has two parameters,

where

is the difference between the forward and backward paths and

is the slope between input and output.

The output of the P-I model is a combination of several backlash operators multiplied by the weight values. Furthermore, the

value determines the slope of the backlash, while the output of the P-I model is stated in Equation 5 (Xie et al., 2018),

P-I model, proven to effectively capture hysteresis behavior, lacks the capability to distinguish the direction of motion, as stated in Equation 3. However, it is only effective for modeling symmetrical non-local memory hysteresis.

2.3. Modified Prandtl-Ishlinskii (MPI) Model

The Prandtl-Ishlinskii (P-I) model is only effective for representing symmetrical hysteresis. To address this shortcoming, the modified Prandtl-Ishlinskii (MPI) model was developed by Kuhnen (2003). Both models are similar, except that a dead-zone operator is integrated at the P-I output. A combination of the backlash and dead-zone operators, enables the MPI to model asymmetric hysteresis. The formular for determining the dead-zone operator is stated in Equation 6 (Xie et al., 2018), while the threshold is shown in Figure 3.

Based on Equation 6, the model output from the combined dead-zone operators multiplied by weights is stated in Equation 7. In addition, the structure of the MPI model is shown in Figure 3(d).

Figure 3 Dead zone with threshold: (a) negative {d<0}, (b) without dead zone {d=0}, and (c) positive {d>0}, (d) the MPI (Modified Prandtl-Ishilinskii) model is composed of combination of several backlash and dead zone operators

The MPI model is formed from a series combination of backlash and dead zone operators. By substituting Equation 5 in 7, the resulting equation for the model output is stated in Equation 8,

where is the output and is the input to the MPI hysteresis model.

The proposed modification of the P-I model effectively captures the asymmetric hysteresis phenomenon. This improvement required additional parameters, potentially leading to a longer computational process. The use of a more elemental model increases the number of parameters to be optimized. Therefore, the trade-off between the model complexity and effectiveness needs to be carefully considered.

Actuator Design

The research developed a multilayer piezoelectric actuator, with the constituent components shown in Figure 4(a). Additionally, Figure 4(b) presents the manufactured parts, while Figure 5 illustrates the corresponding piezoelectric actuator driver circuit. In addition, the manufactured parts and the corresponding piezoelectric actuator driver circuit are shown in Figures 4(b), and 5.

The actuator design parameters obtained from the component measurements shown in Figure 4(b), are summarized in Table 1. The experimental set-up, comprising the piezoelectric actuator, a loadcell used as a displacement sensor, step-up module, driver, and data acquisition card are shown in Figure 6. To enable the usage as a position sensor, the loadcell is calibrated by applying force to the tips and measuring both the displacement and output voltage. The results obtained led to the establishment of a relationship between the loadcell output voltage and the displacement of the tip.

Figure 4(a) The piezoelectric actuator design contains (1) actuator rod, (2) front chassis, (3) spring, (4) piezoelectric crystal, (5) rear chassis, (6) adjustment bolt, (7) washers, (8) lock nut; (b) Piezoelectric actuator components

Figure 5 The piezoelectric actuator driver circuit

Table 1 Actuator's parameters

Figure 6 (a) Block diagram of the experimental setup, (b) The experimental setup to evaluate piezoelectric actuator performance. A load cell is used to measure the actuator displacement

The dynamics of a piezoelectric actuator can be modeled using a second order system as stated in Equation 1. By assuming the hysterical part

and addressing the compensated phenomenon separately as discussed in Section 6, the actuator dynamic model is stated in Equation 9,

Based on Equation 9, the transfer function between the output and is stated in Equation 10,

is stated in Equation 10,

Using the parameters given in Table 1, the transfer function Equation 10 can be stated as 11,

The transfer function in Equation 11 is therefore used to assist in the design of the linear feedback controller.

Estimation of the Hysteresis Parameters

A sinusoidal signal with decreasing amplitude was fed to the driver circuit at low frequency to estimate the P-I and MPI hysteresis model parameters. Initially, the signal had an amplitude of 150V, covering the typical range of actuations in the system. Input at low frequencies puts the piezoelectric in a quasi-static state, minimizing the impact of actuator dynamics on hysteresis, including the rate-dependent effect (Qin, Zhao, and Zhou, 2017; Zhu and Rui, 2016). The frequency of the input signal used for the parameter estimation is 0.1 Hz, and the voltage measurement is stated in Equation 12,

The estimation process was carried out based on Levenberg-Marquardt algorithm using the Simulink^® parameter estimation feature that minimizes the quadratic cost in Equation 13 (MathWorks, 2018).

The Simulink^® models for the P-I and MPI models are shown in Figures 7(a) and (b), respectively.

Figure 7 (a) Simulink^® model of Prandtl-Ishlinskii (P-I) hysteresis, (b) Simulink^® model of Modified Prandtl-Ishlinskii (MPI) hysteresis

The estimated parameters for both P-I and MPI models, comprising a total of 15 elementary models, where each element consists of two and four parameters respectively, are shown in Table 2.

Table 2 (a) The estimated P-I parameters; (b) The estimated MPI parameters

Hysteresis Model Validation

The obtained hysteresis parameter models were validated by comparing the simulation with the experimental outputs. The simulation and experimental results of the P-I and MPI models are shown in Figures 8 and 9(a) including Figures 9(b) and 10, respectively. However, Figures 9(a) and 10(b) show that the deviation between the simulation and experimental outputs of the P-I model are larger than the MPI. Figure 11 shows the comparison of the Root Mean Square Error (RMSE) between P-I and MPI models, in which the P-I model has an RMSE three times larger than that of the MPI.

Figure 8 Simulation and experiment results of P-I Model (a) position output vs input voltage input, (b) position output vs time. There are significant errors between simulation and experiment results on the P-I model

Figure 9 (a) Detailed section on the P-I model validation with a maximum error of 1.4

(b) Simulation and experiment results of the MPI model, position output vs input voltage

Figure 10 Simulation and experiment results of the MPI model (a) position output vs time, (b) detailed section on the MPI model validation. The MPI model yields a better agreement between simulation and experiment compared to the P-I model (Figure 9(b))

Figure 11 Comparison of absolute position error between the P-I and MPI models. RMSE of the P-I model is 0.703 , while RMSE of the MPI model is 0.217

Controller Design

The inverse hysteresis model-feedforward was applied to the controller to compensate for the hysteresis phenomenon in the piezoelectric actuator. Based on Equation 8, the inverse hysteresis model is stated in Equation 14,

The control system proposed in this research consists of a PID and hysteresis inverse model. The PID controller is obtained using Equation 21,

where and K_d are the control command, the position error, and gain, including the integral, and derivative gain, respectively. The PID control algorithm was implemented as a feedback control considering the robustness and broad applicability. It has been used in various applications including the control of medical devices (Irianto et al., 2023) and ICE engines (Abdurrakhman et al., 2020). By adopting an incremental PID algorithm, the overall control input can be derived in a discrete form as stated in Equation 22,

where is the feedback control command in the previous step, and the feedforward term is given by the inverse MPI model. The PID gains were set by using Ziegler–Nichols step response method (Åström and Hägglund, 2004). Figures 12 and 13 show the controller block diagram and the implementation on Simulink^® respectively.

Figure 12 Block diagram of the proposed control system.

Figure 13 Implementation of the proposed controller using Simulink^®

Results and Discussion

Tracking Results

The evaluation of the piezoelectric actuator control system was carried out using two types of controllers. The first experiment used the position control system without an inverse hysteresis model. While the second analysis adopted a position control system with an inverse hysteresis model. The desired position to evaluate the performance of the proposed controller is stated in Equation 23,

Figure 14 shows the response of the position control system without inverse hysteresis model feedforward and the hysteresis phenomenon respectively.

Figure 14 (a) Plot of the desired and measured positions using a PID controller only, (b) Hysteresis phenomenon on the PID controller without the reverse hysteresis model feedforward. The hysteresis phenomenon is around 5mm.

Figure 15 shows the response of the position control system with inverse hysteresis model feedforward and the hysteresis phenomenon, respectively.

Figure 15 (a) Plot of the desired and measured positions using the PID controller with the hysteresis inverse model feedforward, (a) Hysteresis phenomenon on the PID controller with the inverse hysteresis model feedforward. The hysteresis phenomenon is much reduced compared to the PID controller without the feedforward compensation (Figure14(b))

Figure 16 shows a comparison of responses between open loop control with and without inverse model hysteresis compensation. In open loop control, hysteresis values of 4.87 mm and 0.97 mm were observed in without and with the compensation, respectively. This shows that the hysteretic compensator is able to reduce the hysteretic error significantly.

Figure 17 shows a comparison of absolute position errors between two control systems, one using only the PID controller and the other integrating PID controller with the feedforward compensator. It clearly shows that the application of the inverse hysteresis model feedforward can significantly improve the control system performance. Furthermore, the root mean square errors of 1.26 µm and 0.41 µm was obtained for the PID only and the one with feedforward.

Figure 16 Hysteresis comparison between open loop response without compensator ( ) and with the inverse model hysteresis compensator ( ) at 0.2 Hz input signals. The hysteresis compensator is able to reduce the hysteretic error from 4.87 mm to 0.97 mm

Figure 17 Comparison of absolute position errors of the PID controller only and the PID with feedforward compensation. RMSE of the PID controller is 1.26 mm dan for the PID controller with feedforward compensation is 0.41 mm

Conclusion

In conclusion, the design and manufacturing of a piezoelectric-based actuator and the controller were presented. A significant asymmetric hysteretic phenomenon was observed in the piezoelectric actuator. This was addressed by adopting a Modified Prandtl-Ishlinskii (MPI) model and the inverse, which were proposed for incorporation into the position control system, effectively capturing the asymmetric displacement or voltage hysteresis. The parameters in the MPI model were efficiently identified using the Levenberg-Marquardt method. Based on the inverse MPI model, a closed loop control scheme with hysteresis feedforward compensation was proposed. The results of the experiment showed the effectiveness of the proposed MPI model and the inverse in describing the displacement or voltage asymmetric hysteresis of the piezoelectric actuator. In addition, the developed piezoelectric-based micro motion actuator showed good performance with sufficient accuracy.

Acknowledgement

This research was supported by PPMI Ado Lit KK FTMD – ITB.

References

Abdurrakhman, A., Soehartanto, T., Hadi, H.S., Toriki, M.B., Widjiantoro, B.L., Sampurno, B., 2020. Design of Output Power Control System Based on Mass Flow Rate Comparison of Air-Fuel Ratio (AFR) on Dual Fuel Generator Set by Using PID Control Method. International Journal of Technology, Volume 11(3), pp. 574–586

Akbar, M., Ramadhani, M.J., Izzuddin, M.A., Gunawan, L., Sasongko, R.A., Kusni, M., Curiel-Sosa, J.L., 2022. Evaluation on Piezoaeroelastic Energy Harvesting Potential of a Jet Transport Aircraft Wing with Multiphase Composite by means of Iterative Finite Element Method. International Journal of Technology, Volume 13(4), pp. 803–815

Ang, W.T., Khosla, P.K., Riviere, C.N., 2007. Feedforward Controller with Inverse Rate-Dependent Model for Piezoelectric Actuators in Trajectory-Tracking Applications. IEEE/ASME Transactions on Mechatronics, Volume 12(2), pp. 134–142

Apicella, V., Clemente, C.S., Davino, D., Leone, D., Visone, C., 2019. Review of Modeling and Control of Magnetostrictive Actuators. Actuators, Volume 8(2), p. 45

Åström, K.J., Hägglund, T., 2004. Revisiting the Ziegler–Nichols Step Response Method for PID Control. Journal of Process Control, Volume 14(6), pp. 635–650

Cao, Y., Chen, X.B., 2015. A Survey of Modeling and Control Issues for Piezo-electric Actuators. Journal of Dynamic Systems, Measurement, and Control, Volume 137(1), p. 014001

Changhai, R., Lining, S., 2005. Hysteresis and Creep Compensation for Piezoelectric Actuator in Open-Loop Operation. Sensors and Actuators A: Physical, Volume 122(1), pp. 124–130

Damjanovic, D., 2006. Hysteresis in Piezoelectric and Ferroelectric Materials. The Science of Hysteresis, pp. 337–465

Devos, S., Vijver, W.V.d., Mesonero-Romanos, D., Reynaerst, D., Brussel, H.V., 2004. Piezoelectric Motors with a Stepping and a Resonant Operation Mode. In: Proceedings 9^th International Conference on New Actuators, pp. 439–442

Fujii, Y., Endo, Y., Mitsuhata, S., Hayashi, M., Motoyama, H., 2020. Evaluation of The Effect of Piezo?Intracytoplasmic Sperm Injection on The Laboratory, Clinical, and Neonatal Outcomes. Reproductive Medicine and Biology, Volume 19(2), pp. 198–205

Gomis-Bellmunt, O., Ikhouane, F., Montesinos-Miracle, D., 2009. Control of a Piezoelectric Actuator Considering Hysteresis. Journal of Sound and Vibration, Volume 326(3–5), pp. 383–399

Ha, J.-L., Kung, Y.-S., Fung, R.-F., Hsien, S.-C., 2006. A Comparison of Fitness Functions for The Identification of a Piezoelectric Hysteretic Actuator Based on The Real-Coded Genetic Algorithm. Sensors and Actuators A: Physical, Volume 132(2), pp. 643–650

Hassani, V., Tjahjowidodo, T., 2011. Integrated Rate and Inertial Dependent Prandtl-Ishlinskii Model for Piezoelectric Actuator. In: 2011 2^nd International Conference on Instrumentation Control and Automation, IEEE, pp. 35–40

Hassani, V., Tjahjowidodo, T., 2013. Dynamic Modeling of 3-DOF Pyramidal-Shaped Piezo-Driven Mechanism. Mechanism and Machine Theory, Volume 70, pp. 225–245

Hassani, V., Tjahjowidodo, T., Do, T.N., 2014. A Survey on Hysteresis Modeling, Identification and Control. Mechanical Systems and Signal Processing, Volume 49(1–2), pp. 209–233

Heywang, W., Lubitz, K., Wersing, W., 2008. Piezoelectricity - Evolution and Future of a Technology. In: Springer Series in Materials Science, Springer-Verlag Berlin Heidelberg, Berlin

Irianto, B.G., Maghfiroh, A.M., Sofie, M., Kholiq, A., 2023. Baby Incubator with Overshoot Reduction System using PID Control Equipped with Heart Rate Monitoring Based on Internet of Things. International Journal of Technology, Volume 14(4), p. 811–822

Jani, J.M., Leary, M., Subic, A., Gibson, M.A., 2014. A Review of Shape Memory Alloy Research, Applications and Opportunities. Materials & Design (1980-2015), Volume 56, pp. 1078–1113

Karpelson, M., Wei, G.-Y., Wood, R.J., 2012. Driving High Voltage Piezoelectric Actuators in Microrobotic Applications. Sensors and Actuators A: Physical, Volume 176, pp. 78–89

Kuhnen, K., 2003. Modeling, Identification and Compensation of Complex Hysteretic Nonlinearities: A Modified Prandtl-Ishlinskii Approach. European Journal of Control, Volume 9(4), pp. 407–418

Leang, K.K., Devasia, S., 2006. Design of Hysteresis-Compensating Iterative Learning Control for Piezo-Positioners: Application to Atomic Force Microscopes. Mechatronics, Volume 16(3–4), pp. 141–158

Li, Y., Xu, Q., 2009. Design and Optimization of an XYZ Parallel Micromanipulator with Flexure Hinges. Journal of Intelligent and Robotic Systems, Volume 55(4–5), pp. 377–402

Lin, C.-J., Yang, S.-R., 2006. Precise Positioning of Piezo-Actuated Stages Using Hysteresis-Observer Based Control. Mechatronics, Volume 16(7), pp. 417–426

Matsuda, S., Matsuo, T., Ueyama, M., 2001. Micro Actuator with Two Piezoelectric Elements Placed at Right Angles. Human Friendly Mechatronics, Elsevier, pp. 143–148

MathWorks, 2018. Least-Squares (Model Fitting) Algorithms, Accessed: December 5, 2022. Available: https://www.mathworks.com/help/optim/ug/least-squares-model-fitting algorithms.html

MATLAB, 2023, Version R2023b, License No: 40908710, Natick, Massachusetts: The MathWorks Inc.

Polit, S., Dong, J., 2011. Development of a High-Bandwidth XY Nanopositioning Stage for High-Rate Micro-/Nanomanufacturing. IEEE/ASME Transactions on Mechatronics, Volume 16(4), pp. 724–733

Qin, F., Zhang, D., Xing, D., Xu, D., Li, J., 2020. Laser Beam Pointing Control with Piezoelectric Actuator Model Learning. IEEE Transactions on Systems, Man, and Cybernetics: Systems, Volume 50(3), pp. 1024–1034

Qin, Y., Zhao, X., Zhou, L., 2017. Modeling and Identification of the Rate-Dependent Hysteresis of Piezoelectric Actuator Using a Modified Prandtl-Ishlinskii Model. Micromachines, Volume 8(4), p. 114

Rodriguez-Fortun, J.M., Orus, J., Alfonso, J., Buil, F., Castellanos, J.A., 2011. Hysteresis in Piezoelectric Actuators: Modeling and Compensation. IFAC Proceedings Volumes, Volume 44(1), pp. 5237–5242

Tian, Y., Zhang, D., Shirinzadeh, B., 2011. Dynamic Modelling of a Flexure-Based Mechanism for Ultra-Precision Grinding Operation. Precision Engineering, Volume 35(4), pp. 554–565

Wang, D.H., Zhu, W., 2011. A Phenomenological Model for Pre-Stressed Piezoelectric Ceramic Stack Actuators. Smart Materials and Structures, Volume 20(3), p. 035018

Xie, S., Mei, J., Liu, H., Wang, Y., 2018. Hysteresis Modeling and Trajectory Tracking Control of The Pneumatic Muscle Actuator Using Modified Prandtl–Ishlinskii Model. Mechanism and Machine Theory, Volume 120, pp. 213–224

Xu, Q., Li, Y., 2010. Precise Tracking Control of a Piezoactuated Micropositioning Stage Based on Modified Prandtl-Ishlinskii Hysteresis Model. In: 2010 IEEE International Conference on Automation Science and Engineering, IEEE, pp. 692–697

Zheng, J., Fu, M., Lu, R., Xie, S., 2018. Design, Identification, and Control of a Linear Dual-Stage Actuation Positioning System. Journal of the Franklin Institute, Volume 355(12), pp. 5018–5036

Zhu, W., Rui, X.-T., 2016. Hysteresis Modeling and Displacement Control of Piezoelectric Actuators with The Frequency-Dependent Behavior Using a Generalized Bouc–Wen Model. Precision Engineering, Volume 43, pp. 299–307

Zhu, W., Wang, D., 2012. Non-symmetrical Bouc–Wen Model for Piezoelectric Ceramic Actuators. Sensors and Actuators A: Physical, Volume 181, pp. 51–60

Download PDF

Who cite this paper

Table of Contents

Article