Target Strength of Eels from Echosounder and Calibrated Fish Finder Using Acoustic Measurement and Numerical Model
Corresponding email: angga.dwinovantyo@brin.go.id
Published at : 17 Jul 2025
Volume : IJtech
Vol 16, No 4 (2025)
DOI : https://doi.org/10.14716/ijtech.v16i4.6525
Dwinovantyo, A, Triyanto, Triwisesa, E, Samir, O, Haryani, GS, Wibowo, H, Hidayat, Sulawesty, F, Nafisyah, E, Lukman, Ali, F & Setiawan, FA 2025, ‘Target strength of eels from echosounder and calibrated fish finder using acoustic measurement and numerical model’, International Journal of Technology, vol. 16, no. 4, pp. 1323-1336
| Angga Dwinovantyo | Research Center for Deep Sea, The National Research and Innovation Agency (BRIN), Jl. Pasir Putih Raya No.1, Jakarta 14430, Indonesia |
| Triyanto | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Endra Triwisesa | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Octavianto Samir | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Gadis Sri Haryani | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Hendro Wibowo | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Hidayat | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Fachmijany Sulawesty | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Eva Nafisyah | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Lukman | Research Center for Limnology and Water Resources, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Fauzan Ali | Research Center for Fisheries, The National Research and Innovation Agency (BRIN), Jl. Raya Bogor Km. 46, Cibinong, West Java 16911, Indonesia |
| Foni Agus Setiawan | Research Center for Data and Information Science, The National Research and Innovation Agency (BRIN), Jl. Sangkuriang No. 21, Bandung, West Java 40135, Indonesia |
Acoustics methods are essential in surveying and assessing fish stocks in aquatic environments, utilizing both conventional fish finders and scientific echosounders. Although fish finders can provide acoustic backscatter information, scientific echosounders give more precise measurements since their settings are calibrated. The present study investigates the acoustic backscattering characteristics of eels (Anguilla sp.) using a calibrated fish finder (Furuno FCV-628) and a scientific echosounder (Simrad EK15), both operating at 200 kHz. Discrete targets were identified in the water column by quantifying their backscattering values. The Distorted-Wave Born Approximation (DWBA) and Kirchhoff-Ray mode (KRM) models were adopted to estimate the theoretical dorsal and lateral backscatter as a function of frequency and length for each eel. Results showed that the calibrated fish finder could effectively distinguish target strength variations, offering comparable outcomes to scientific echosounders and numerical models, particularly across different eel lengths.
Acoustic backscattering; Calibrated fish finder; Eel; Numerical models, Scientific echosounder
Eel is a fish species found particularly in Lake Poso, Sulawesi Island, Indonesia. It is categorized as a high-value target species in the local fishery industry due to its high economic potential (Moeis et al., 2024). The life cycle of eels comprises various stages, each characterized by distinct shapes and sizes, ranging from the transparent bodies of glass eels to the more robust and pigmented forms of elvers and adult eels. (Lukman et al., 2021; Triyanto et al., 2021). Given this scenario, the Industrial Revolution 4.0 has introduced innovative methods for monitoring eel to ensure sustainability, including the use of underwater acoustics to track behavior and migration patterns (Surjandari et al., 2022).
Acoustic technology is critically important in fisheries studies (Zang et al., 2021; Lagarde et al., 2020; Becker and Suthers, 2014). In this context, the industrial exploration and monitoring standard, specifically for migratory fishes, include using a scientific echosounder to measure volume backscattering strength (SV) and target strength (TS) to estimate fish size, biomass, and distribution patterns with high accuracy and non-invasive methods (Popper et al., 2020). It is important to note that acoustic methods are quantitative, operate in quasi-real time, and are not limited by light availability or high turbidity, which facilitates their increasing use in aquatic studies (Martignac et al., 2015). However, these methods still face limitations in terms of operational flexibility, portability, and equipment compatibility. While scientific echosounders offer clear advantages for measuring TS, calibrated fish finders can also provide useful acoustic backscatter data for research. Both instruments are capable of rapidly estimating aquatic populations such as fish abundance, and tracking migratory movements along with spatial and temporal distribution patterns, particularly for eels (Anguilla spp.) (Shen et al., 2024; Noda et al., 2021; Howe et al., 2019; MacLennan and Fernandes, 2008).
A general limitation of conventional fish finders is the lack of TS and SV outputs data required for post-processing. In contrast, scientific echosounders provides more accurate and reliable acoustic backscattering measurements. Data from conventional fish finders tend to lack precision, as these devices are primarily designed for fishing activities rather than scientific analysis. However, it is possible to calibrate the acoustic backscatter values. The raw, uncalibrated signal typically includes echoes from various objects in the water column (Winfield et al., 2009). To obtain precise TS measurement of the target, a conventional fish finder must be calibrated by analyzing the echo pattern of individual targets and adjusting the instrument settings to minimize electrical interference and false echoes (Demer et al., 2015).
Recent advancements in eel research have been supported by the application of modern acoustic methods. These techniques have contributed to a more detailed understanding of eel behavior and migration patterns (Noda et al., 2021; Popper et al., 2020). In this context, the use of single beam echosounders such as the Simrad EK15 and Furuno FCV-628, both operating at a frequency of 200 kHz, has proven particularly valuable. Verifying the consistency of results obtained from these two types of acoustic instruments is essential for ensuring data reliability (Rautureau et al., 2022). The Simrad EK15, equipped with a high-resolution and compact narrowband transducer, has been instrumental in capturing detailed acoustic characteristics of fish (Fauziyah et al., 2023; Linløkken et al., 2019; Betanzos et al., 2015). On the other hand, the Furuno FCV-628 offers exceptional resolution (Manik et al., 2020), flexible raw data output, and effective target separation (Dwinovantyo et al., 2023), making it a useful tool for monitoring and studying eels in natural habitats.
To obtain accurate acoustic backscatter measurements, several parameters on acoustic devices must be properly calibrated (Demer et al., 2015). Calibration is typically performed by measuring the TS of a reference sphere under controlled laboratory conditions (Manik et al., 2017). The TS of eels has been determined across various body lengths, with results showing variation in TS values depending on size (Dunning et al., 2023; Pratt et al., 2021). These measurements are generally conducted in a small water tank using a horizontal beam orientation to ensure consistent and controlled conditions (Kim et al., 2018).
In fish acoustic measurements, comparing experimentally measured TS with theoretical values derived from models such as the Kirchhoff-Ray Mode (KRM) and the Distorted-Wave Born Approximation (DWBA) is essential for validating results and improving acoustic methodologies. In this study, the KRM model was used to estimate the theoretical TS of elvers and adult eels, while the DWBA model was applied to glass eels (Macaulay et al., 2013; Horne et al., 2000). The challenges in conventional fish finders are to be addressed by quantifying backscatter in digital numbers, which were then converted into TS in decibels (dB). This study fills an important gap in eel acoustics by combining acoustic measurements at a single frequency with model-based TS estimates, enabling a stronger connection between empirical data and numerical simulations.
2.1. Experimental Design
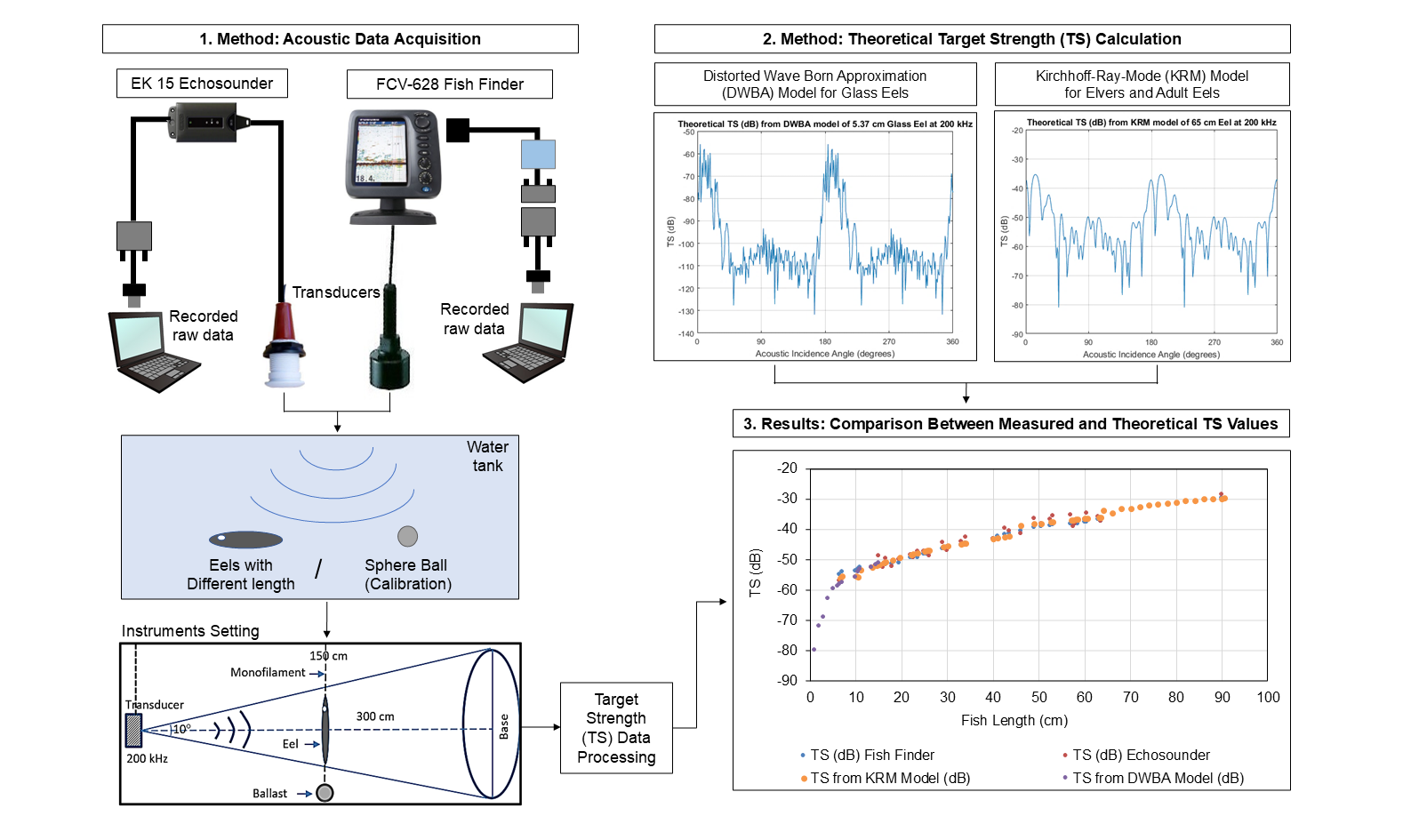
In the experimental setup of this study, the acoustic acquisition was carried out using alternating deployments of a scientific echosounder Simrad EK15 (Simrad Kongsberg Maritime AS, Horten, Norway) and a fish finder Furuno FCV-628 (FURUNO ELECTRIC CO., LTD, Hyogo, Japan) for individual eel across a range of lengths. A reference sphere was used concurrently as a calibration control (Demer et al., 2015). The experimental design aimed to identify potential size-related patterns in acoustic signatures by systematically varying the body length of the eels. The EK15 operated with dedicated software integrated into a pre-built interface hardware system, allowing direct communication and control during measurements. In contrast, the FCV-628 was connected via a serial converter, with data acquisition and recording managed through TeraTerm software (Dwinovantyo et al., 2023). A schematic diagram showing the interface setup for both the fish finder and the echosounder is presented in Figure 1.
Figure 1 Schematic of experimental data acquisition for eel TS measurement in the controlled water tank contrasting acquired data with theoretical TS derived from numerical models for comprehensive analysis
Raw data obtained from acoustic measurements were processed using procedures based on the sonar equation (Manik et al., 2020). The processed results were then compared with theoretical outputs from the KRM and DWBA models to evaluate their accuracy and consistency. To explore potential relationships and trends within the data, simple linear regression was applied as the primary statistical analysis method.
2.2. Data Acquisition
The tools used in this study included a single-beam fish finder Furuno FCV-628 and a single-beam scientific echosounder Simrad EK15, both operating at a frequency of 200 kHz. Additional materials consisted of eels of various sizes, reference spheres for calibration, and a monofilament line. The detailed settings of the acoustic instruments are presented in Table 1.
Table 1 Tool settings during data acquisition and water conditions in the water tank
The study procedure began with the calibration of the fish finder using a reference sphere, followed by the measurement of eel acoustic data using each instrument in a water tank maintained at a constant temperature of 27°C. TS measurements were performed on 69 anesthetized live eels, ranging in size from 6.5 to 90 cm. The transducers were mounted horizontally at a depth of approximately 0.5 meters below the water surface, with various beam orientations applied during the measurements (Kerschbaumer et al., 2020; Kurnia et al., 2011).
2.3. Data Analysis
Raw acoustic data were converted into acoustic backscattering values, expressed in decibels (dB). The data were obtained using TeraTerm software for Furuno FCV-628 fish finder and Simrad EK15 acquisition version 1.2.4 software for scientific echosounder. When an acoustic signal encounters a targets or object, the characteristic measure of the scattering strength is referred to as the specific scattering power. This is defined by (Nishiyama, 2017) and is calculated using Equation 1:
where TS is target strength (dB), EL is echo level (dBV), KTR is the factor of transmitting and receiving (dBV), R is water range from the transducer to object (m), and
is absorption coefficients (dB km-1). KTR is an unknown parameter for users and was calibrated by the manufacturer. Subsequently, the measured TS from both instruments were compared (Rautureau et al., 2022).
The observed fish TS was primarily considered a function of the length and orientation or angle of inclination. The length and angle of inclination from the observation conducted are presented in Equation 2 (Furusawa and Amakasu, 2010):
where L is the length of fish (m), is the angle of inclination of fish (°), fa(
) is the probability density function (PDF) of the tilt angle, and fb(L) is the PDF of the length of fish. Results obtained from measuring the reflected acoustic strength with variations in the angle and acoustic sounding points on the back (dorsal), abdomen (ventral), as well as the side of each target were compared and averaged to obtain the mean TS value. Equation 2 can be derived from the relationship between the length and average TS, as shown in Equation 3:
where LAvg is the mean of fish length, and L is the standard deviation. TScm was calculated from the average TS measured and average fish length, alongside the standard deviation obtained from the measured length (Dunning et al., 2023). This suggested that the standard deviation of the variation in length was relatively small. Additionally, the average and mean TS were assumed to be equal.
2.4. Numerical Model
In this study, two numerical models were employed, each suited to a different life stage of eel. The KRM model was used to calculate the theoretical TS calculations of adult eels, while DWBA model was applied for glass eels.
2.4.1. Kirchhoff-ray Mode (KRM) Model
KRM model was used to theoretically estimate acoustical backscattering characteristics of the dorsal and lateral of eels as a function of fish length, aspect, and frequency (Lan-yue et al., 2021). This model adopted a fish-shaped base resembling fluid and gas-filled cylinders representing the body and swimbladder, respectively. The acoustic backscattering is presented in Equation 4:
and swimbladder is shown in Equation 5 as:
where l(f) is scattering amplitude as a function of carrier frequency, k is the wave number (2/
) which depends on the frequency and sound speed at water medium,
is the acoustical wavelength, a is the radius of the cylinder, fb is fish body, w is water, sb is swimbladder, and
u(j) is the cumulative distance between cylinder at the midpoint (Li et al., 2023). The backscattering cross-section (
bs) from the scattering amplitude was calculated in Equation 6, while the theoretical TS of the eel was presented in Equation 7.
where TL is transmission losses. The theoretical TS was calculated individually for fish body and swimbladder, before being summed.
2.4.2. Distorted-wave Born Approximation (DWBA) Model
General mathematical equations for scattering amplitude in DWBA model are expressed in Equation 8:
where fbs is the backscattering amplitude, k1 is the acoustic wave number, r0 is the position vector, rpos value is the position in a particular line of the body axis. The material properties of glass eel bodies, namely , and
, were expressed in Equation 9 (Jech et al., 2015):
where g is density contrast, h is sound speed contrast, and is compressibility which is presented in Equation 10:
where is mass density, and c is sound speed. DWBA model, used in weak scatterers, is valid for all acoustic frequencies, the angle of orientation, and shapes of glass eels. Furthermore, g and h from other studies were considered to be used based on the acoustic properties of the weakly scattering sphere of fluid-like bodies (Jech et al., 2015). Density (
) and sound speed (c) in glass eels’ bodies were 1028 kg m-3 and 1480.3 m s-1, respectively, against the surrounding medium of 1026.9 kg m-3 and 1477.4 m s-1 (Kusdinar et al., 2014).
3.1. Calibration
The results of fish finder calibration using a sphere, produced output in the form of raw data, which were then extracted using spreadsheet software. The output consists of an index of setting, depth, and echo data record, as shown in Figure 2.
Figure 2 Raw data output in one ping data from the fish finder
The data format adhered to the NMEA0183 proprietary sentence standard compatible with a baud rate of 38400bps. In the raw data, PFEC SDes1, which contained frequency, power, pulse width, data type, start depth, resolution, and the number of data, was used to index the setting. PFEC SDes2 contained the depth of measurement, while PFEC SDesd contained raw data from the echosounder without TVG compensation.
The calibration was conducted to verify whether the fish finder could accurately measure the sphere ball (Kim et al., 2018). TS pattern was calculated and compared to the theoretical model, and the measured results agreed with the model, confirming the accuracy. Subsequently, data from recorded pings were compared and averaged to verify data consistency. The calibration results are shown in Figure 3.
Figure 3 (a) represents the first and second echo on each ping from TS measurements. The first echo signified backscattering from the surface of the water to the bottom, which included the backscattering strength of the sphere ball, while the second echo showed the reflection from the bottom of the water. The measurement results also signified noise at the surface, caused by the near field at 0-0.5 m. The results obtained were an average value of 188 from 100 pings, as well as minimum and maximum values of 152 and 211, respectively. The reflected strengths were then processed into decibels (dB). Figure 3 (b) represents the sonar equation conversion results as an echogram which considered parameters such as transmission losses and sound absorption by the water medium. The average TS of the sphere, calculated using Equation 1, was -40.55 dB, while the theoretical value for a standard sphere ball, was -41.0 dB (Demer et al., 2015).
(a)
(b)
Figure 3 (a) The raw data and (b) processed data of the sphere ball from the fish finder
3.2. Measured TS pattern and orientation of eel
The average echo isolation was used to distinguish the measured echo value from surrounding reflections (Dunning et al., 2023). Echoes with peak values significantly higher than the surrounding signal were classified as single echoes. TS values obtained from the variation in measurement angles, namely dorsal, ventral, and both sides of the eels, are shown in Figure 4.
Eels were measured at depth ranging from 1.4-1.6 m, where higher acoustic peaks were observed. The TS values on the dorsal side were generally higher, likely because the entire surface of the head and swimbladder reflected the sound, resulting in a high digital value. The swimbladder, being filled with air, produced a strong acoustic response due to the impedance contrast between water and air (Gauthier and Horne, 2004).
Figure 4 The results of measuring acoustic values on the dorsal or upper (blue), ventral or downside (red), left (green), and right side (yellow) of the eel
3.3. TS of eel from numerical models
3.3.1. KRM Model
The comparison between TS values measured in the laboratory and those estimated using the KRM model can vary depending on several factors, including the fish species, experimental condition, and the modeling assumptions (Reeder et al., 2004). The integration of experimental measurements with numerical modeling offered a more comprehensive understanding of TS behavior and variability in fish, as illustrated in Figure 5.
(b)
Figure 5 (a) Digitized shape of eel in cylinder form with swimbladder (red color) and interval 16 mm; (b) The theoretical TS pattern related to tilting angle from digitized shape of eel generated by KRM model
The results were based on assumptions regarding the shape, size, and internal structure of the fish (Kusdinar et al., 2014). In this study, the KRM model was applied specifically to elvers and adult eels, as it effectively represented TS across all range frequencies and under near-normal incidence conditions. TS values generated from KRM model showed various results based on the acoustic incidence angle or fish orientation. The model calculated the acoustic backscatter from a three-dimensional representation of both the swimbladder and the fish body (Macaulay et al., 2013). Figure 5 (a) illustrates the acoustic scattering pattern at the 200 kHz digitizing interval for the fish and swimbladder. Meanwhile, Figure 5(b) presents the modeled TS pattern based on the combined geometry of the swimbladder and fish body. It Is important to note that the results shown in Figure 5 (b) varied with a change in pitch angle, where the impact on scattering strength was greater at higher frequencies. The highest TS values were observed within a pitch angle range of -10° to 0°, corresponding to the tilt angle of the swimbladder (Tong et al., 2022).
The orientation of fish relative to the incident sound wave can affect TS values, due to varying scattering characteristics in different directions. At an incidence angle of at 0° (dorsal aspect) and 180° (ventral aspect), the main lobes from a 65 cm eel at 200 kHz displayed a similar shape, both yielding higher TS values. The dorsal and ventral aspects exhibited greater scattering angles compared to other orientations, resulting in stronger sound wave reflections (Reeder et al., 2004). All eels' sizes were modeled and the results showed consistent patterns. It is important to note that the acoustics response from different sizes of eels primarily depends on the area and rugosity of the swimbladder surface and body. Eels possessing swimbladders exhibited resonance effects at specific frequencies, which could enhance or reduce TS values depending on factors such as incident frequency, swimbladder size, shape, and gas content (Li et al., 2023).
3.3.2. DWBA Model
The KRM model has limitations when applied to weak scatterers, such as glass eels (Jech et al., 2015). This is because the model was based on ray theory, which assumed the scatterers were larger than the wavelength of the incident sound wave. Additionally, it primarily accounts for specular reflections from the surface of the scatterer (Li et al., 2023).
Glass eels, however, are small and possess relatively smooth bodies, which may not satisfy the assumptions required by the KRM model. In such cases, DWBA model is more suitable for predicting scattering as it can accommodate smaller and weaker scatterers (Jech et al., 2015). The DWBA model incorporates the size, shape, composition, and orientation of the target, enabling more accurate predictions of scattering behavior in glass eels. For this analysis, fish shapes were digitized and used to generate meshes for TS estimation, as illustrated in Figure 6.
(a) (b)
Figure 6 (a) The digitized 5.37 cm glass eel; (b) The theoretical TS compared to the acoustic incidence angle at 200 kHz generated by DWBA model
The dorsal and ventral aspects of the fish, corresponding to incidence angles of 0° and 180° respectively, are generally more exposed to the incoming sound wave because they face directly toward the acoustic source. This positioning allows for more direct scattering, which often results in higher TS values. Additionally, the body shape and orientation influence how sound waves are scattered. The larger surface area of the dorsal and ventral sides reflects more sound energy, further contributing to increased TS values.
TS curves produced using the KRM model consistently showed smoother frequency response profiles with smaller amplitude fluctuations. This suggests that TS estimates from the KRM model exhibit lower variability and offer greater statistical reliability across the frequency spectrum compared to those from the DWBA model. As shown in Figures 5 (b) and 6 (b), this trend aligns with the central limit theorem, which states that increasing the sample size tends to reduce both the range and the standard deviation of the data distribution.
3.4. Statistical analysis
After obtaining TS values of eels from both numerical models, the data were plotted and compared with laboratory measurement results, as shown in Figure 7. In this figure, the purple color represents the TS value derived from the DWBA model, which were based on eel lengths obtained from digitized images during the glass eel phase. The orange data points indicate TS values generated by the KRM model, covering the elver to adult eel stages. To evaluate the relationship between model outputs and measured values, simple linear regression analysis was applied. TS values obtained from the KRM model demonstrated a strong correlation with experimental measurements, as shown by the nearly parallel regression lines. In contrast, TS values from the DWBA model tended to be higher than the measured values.
Figure 7 TS results (dB) from the direct measurements in the laboratory and the 2 numerical models, compared to the length of eel (in cm)
KRM model is more appropriate for solid-shaped fish, while the DWBA is more suitable for soft-bodied organisms such as zooplankton (Jech et al., 2015). DWBA assumes that the target organism has soft, smooth surface, which does not accurately represent the complex shape and rough surface of elver and adult eels. As a result, DWBA may not fully capture the scattering and reflection of sound waves from these irregular surfaces, potentially leading to an overestimation of TS values. In this study, it was not possible to clearly distinguish between TS measurements obtained in the laboratory and those predicted by the DWBA model for fish measuring between 1 and 5 cm in length.
TS values from both the numerical models and laboratory measurements showed a positive correlation with fish length (Dunning et al., 2023; Hananya et al. 2020). Previous studies have also established a relationship between fish length and TS across various marine species (Frouzova et al., 2005). This study found a strong correlation between TS values obtained from the echosounder and fish finder when compared to those predicted by the KRM and DWBA models, while also recognizing several limitations. The research involved two eel species, Anguilla bicolor bicolor and Anguilla marmorata, which differ in morphology and behavior. These biological differences contributed to variability in the relationship between fish length and TS.
Further comparisons were made between TS measurements collected from the echosounder and the calibrated fish finder. The results showed no statistically significant difference in mean TS values across different eel lengths, as determined by simple linear regression analysis (p-value > 0.05). Moreover, graphical representations in Figure 8 illustrate a high level of consistency between the datasets acquired using the EK15 echosounder and the FCV-628 fish finder, regardless of fish size.
Figure 8 The results of numerical models and laboratory measurements using simple linear regression analysis
The significance and advantages of this study lie in its potential applications and cost-effectiveness. The findings demonstrated that a calibrated fish finder can accurately measure fish of various sizes within the water column. To improve the validity and generalizability of these results, future research should consider increasing the sample size to include a wider range of specimens. Investigating eel populations from diverse geographic regions or ecological settings would also enhance the broader applicability of the findings. Data collected from acoustic instruments can be further analyzed using artificial intelligence (AI), with machine learning algorithms employed to identify patterns and trends (Berawi, 2020), particularly in the context of monitoring eels. Additionally, AI offers the potential to automate routine and repetitive tasks involved in acoustic data acquisition and processing (Asvial et al., 2023), thereby increasing efficiency and reducing manual effort.
In conclusion, the TS measurement method was applied to 69 eels in a small water tank using a calibrated fish finder at 200 kHz. The results demonstrated a clear positive relationship between eel body length and TS values, with the highest TS observed from dorsal and ventral aspects due to greater acoustic reflectivity, while side orientations produced comparatively lower values. Numerical modeling further supported these findings: the Kirchhoff-Ray Mode (KRM) model showed a strong correlation with measured TS values, particularly for elvers and adult eels, making it a reliable tool for TS prediction in solid-bodied fish. In contrast, the Distorted-Wave Born Approximation (DWBA) model, more suitable for soft-bodied organisms, tended to overestimate TS, especially in smaller eels, due to its assumptions about body composition and surface smoothness. Importantly, no significant statistical difference was found between the TS data collected using the echosounder and the fish finder, highlighting the potential of using a calibrated fish finder as a practical and cost-effective alternative for acoustic fish monitoring. This approach provides new insights into eel detection and size estimation based on TS values. Future studies should consider larger and more diverse samples, as well as integrating artificial intelligence techniques to enhance data analysis and automate acoustic processing for broader ecological applications.
The publication is prepared within the framework of the LPDP Rispro Invitation Program No. PRJ-54/LPDP/2020 under the "Continuity of Anguillids Eels Production as Migratory Fish in Central Sulawesi Lakes and Poso River to Support Food Sustainability" project.
| Filename | Description |
|---|---|
| R1-EECE-6525-20240328091324.png | Figure 1 (*.png) for better clarity |
Asvial, M, Zagloel, TYM, Fitri, IR, Kusrini, E & Whulanza, Y 2023, 'Resolving engineering, industrial and healthcare challenges through AI-driven applications', International Journal of Technology, vol. 14, no. 6, pp. 1177–1184, https://doi.org/10.14716/ijtech.v14i6.6767
Becker, A & Suthers, IM 2014, 'Predator driven diel variation in abundance and behavior of fish in deep and shallow habitats of an estuary', Estuarine, Coastal and Shelf Science, vol. 144, pp. 82–88, https://doi.org/10.1016/j.ecss.2014.04.012
Berawi, MA 2020, 'Managing artificial intelligence technology for added value', International Journal of Technology, vol. 11, no. 1, pp. 1–4, https://doi.org/10.14716/ijtech.v11i1.3889
Betanzos, A, Martín, HA, Tizol, SVR, Schneider, P, Hernández, JL, Brehmer, P, Linares, EO, Guillard, J & Hermand, JP 2015, 'Performance of a low-cost single beam echosounder: In situ trials in a shallow water coral reef habitat with verification by video', In: 2015 IEEE/OES Acoustics in Underwater Geosciences Symposium (RIO Acoustics), pp. 1–3, https://doi.org/10.1109/RIOAcoustics.2015.7473629
Demer, DA, Berger, L, Bernasconi, M, Bethke, E, Boswell, KM, Chu, D, Domokos, R, Dunford, A, Fässler, S & Gauthier, S 2015, 'Calibration of acoustic instruments', ICES Cooperative Research Report, vol. 326, pp. 1–133, http://dx.doi.org/10.25607/OBP-185
Dunning, J, Jansen, T, Fenwick, A & Fernandes, P 2023, 'A new in-situ method to estimate fish target strength reveals high variability in broadband measurements', Fisheries Research, vol. 261, article 106611, https://doi.org/10.1016/j.fishres.2023.106611
Dwinovantyo, A, Solikin, S, Triwisesa, E & Triyanto, T 2021, 'Target strength of Nile tilapia (Oreochromis niloticus) from 200 kHz calibrated fish finder and scientific echosounder: laboratory measurement and modeling', IOP Conference Series: Earth and Environmental Science, vol. 1251, article 012022, https://doi.org/10.1088/1755-1315/1251/1/012022
Fauziyah, F, Ningsih, EN, Arnando, E, Fatimah, F, Agustriadi, F & Supriyadi, F 2023, 'Effect of hauling and soaking time of stationary lift nets on fish aggregation using a hydroacoustic monitoring approach', Egyptian Journal of Aquatic Research, vol. 49, no. 3, pp. 339–346, https://doi.org/10.1016/j.ejar.2023.05.003
Frouzova, J, Kubecka, J, Balk, H & Frouz, J 2005, 'Target strength of some European fish species and its dependence on fish body parameters', Fisheries Research, vol. 75, pp. 86–96, https://doi.org/10.1016/j.fishres.2005.04.011
Furusawa, M & Amakasu, K 2010, 'The analysis of echotrace was obtained by a split-beam echosounder to observe the tilt-angle dependence of fish target strength in situ', ICES Journal of Marine Science, vol. 67, pp. 215-230, https://doi.org/10.1093/icesjms/fsp246
Gauthier, S & Horne, JK 2004, 'Potential acoustic discrimination within boreal fish assemblages', ICES Journal of Marine Science, vol. 61, no. 5, pp. 836–845, https://doi.org/10.1016/j.icesjms.2004.03.033
Hananya, A, Pujiyati, S, Hasbi, MS & Retnoaji, B 2020, 'Indonesian short fin eel Anguilla bicolor (Mclelland, 1844) swim bladder as important organ for reflecting acoustic wave', IOP Conference Series: Earth and Environmental Science, vol. 429, article 012017, https://doi.org/10.1088/1755-1315/429/1/012017
Horne, JK, Walline, PD & Jech, JM 2000, 'Comparing acoustic model predictions to in situ backscatter measurements of fish with dual?chambered swimbladders', Journal of Fish Biology, vol. 57, no. 5, pp. 1105-1121, https://doi.org/10.1111/j.1095-8649.2000.tb00474.x
Howe, BM, Miksis-Olds, J, Rehm, E, Sagen, H, Worcester, PF & Haralabus, G 2019, 'Observing the oceans acoustically', Frontiers in Marine Science, vol. 6, article 426, https://doi.org/10.3389/fmars.2019.00426
Jech, JM, Horne, JK, Chu, D, Demer, DA, Francis, DT, Gorska, N, Jones, B, Lavery, AC, Stanton, TK, Macaulay, GJ, Reeder, B & Sawada, K 2015, 'Comparisons among ten models of acoustic backscattering used in aquatic ecosystem research', The Journal of the Acoustical Society of America, vol. 138, pp. 3742-3764, https://doi.org/10.1121/1.4937607
Kerschbaumer, P, Tritthart, M & Keckeis, H 2020, 'Abundance, distribution, and habitat use of fishes in a large river (Danube, Austria): mobile, horizontal hydroacoustic surveys vs. a standard fishing method', ICES Journal of Marine Science, vol. 77, no. 5, pp. 1966–1978, https://doi.org/10.1093/icesjms/fsaa081
Kim, H, Kang, D, Cho, S, Kim, M, Park, J & Kim, K 2018, 'Acoustic target strength measurements for biomass estimation of aquaculture fish, redlip mullet (Chelon haematocheilus)', Applied Science, vol. 8, article 1536, https://doi.org/10.3390/app8091536
Kurnia, M, Iida, K & Mukai, T 2011, 'Measurement and modelling of three-dimensional target strength of fish for horizontal scanning sonar', Journal of Marine Science and Technology, vol. 19, no. 3, pp. 287-293, https://doi.org/10.51400/2709-6998.2194
Kusdinar, A, Hwang, B & Shin, H 2014, 'Determining the target strength bambood wrasse (Pseudolabrus japonicus) using Kirchhoff-ray mode', Journal of the Korean Society of Fisheries Technology. The Korean Society of Fisheries and Ocean Technology, vol. 50, no. 4, pp. 427–434, https://doi.org/10.3796/KSFT.2014.50.4.427
Lagarde, R, Peyre, J, Amilhat, E, Mercader, M, Prellwitz, F, Simon, G & Faliex, E 2020, 'In situ evaluation of European eel counts and length estimates accuracy from an acoustic camera (ARIS)', Knowledge and Management of Aquatic Ecosystems, vol. 421, article 44, https://doi.org/10.1051/kmae/2020037
Lan-yue, Z, Yu-tong, S, Yi, Y, De-sen, Y & Gui-lin, Z 2021, 'Study on acoustic scattering characteristics of fish', 2021 OES China Ocean Acoustics (COA), pp. 250–255, https://doi.org/10.1109/COA50123.2021.9519886
Li, C, Chu, D, Horne, J & Li, H 2023, 'Comparison of coherent to incoherent Kirchhoff-ray-mode (KRM) models in predicting backscatter by swim-bladder-bearing fish', Journal of Marine Science and Engineering, vol. 11, no. 3, article 473, https://doi.org/10.3390/jmse11030473
Linløkken, AN, Næstad, F, Langdal, K & Østbye, K 2019, 'Comparing fish density and echo strength distribution recorded by two generations of single beam echo sounders', Applied Sciences, vol. 9, no. 10, article 2041, https://doi.org/10.3390/app9102041
Lukman, L, Triyanto, T, Haryani, GS, Samir, O, Gogali, L & Bandjolu, KP 2021, 'Eel (Anguilla spp.) fishing activity in Poso Area Central Sulawesi, Indonesia', IOP Conference Series: Earth and Environmental Science, vol. 869, article 012022, https://doi.org/10.1088/1755-1315/869/1/012022
Macaulay, GJ, Peña, H, Fässler, SM, Pedersen, G & Ona, E 2013, 'Accuracy of the Kirchhoff-approximation and Kirchhoff-ray-mode fish swimbladder acoustic scattering models', PLOS ONE, vol. 8, no. 5, article e64055, https://doi.org/10.1371/journal.pone.0064055
MacLennan, DN & Fernandes, PG 2008, 'Fish abundance estimation using hydroacoustics', In: Simmonds, J. (Ed.), Fisheries Acoustics: Theory and Practice, Blackwell Publishing Ltd, Oxford, UK, pp. 145-200
Manik, HM, Apdillah, D, Dwinovantyo, A & Solikin, S 2017, 'Development of quantitative single beam echosounder for measuring fish backscattering', In: Advances in Underwater Acoustics, pp. 119-133
Manik, HM, Nishimori, Y, Nishiyama, Y, Hazama, T, Kasai, A, Firdaus, R, Elson, L & Yaodi, A 2020, 'Developing signal processing of echo sounder for measuring acoustic backscatter', IOP Conference Series: Earth and Environmental Science, vol. 429, article 012034, https://doi.org/10.1088/1755-1315/429/1/012034
Martignac, F, Daroux, A, Bagliniere, JL, Ombredane, D & Guillard, J 2015, 'The use of acoustic cameras in shallow waters: new hydroacoustic tools for monitoring migratory fish population. A review of DIDSON technology', Fish and Fisheries, vol. 16, no. 3, pp. 486-510, https://doi.org/10.1111/faf.12071
Moeis, AO, Gita, AA, Destyanto, AR, Rahman, I, Hidayatno, A & Zagloel, TY 2024, 'Policy analysis of coastal-based special economic zone development using system dynamics', International Journal of Technology, vol. 15, no. 1, pp. 195-206, https://doi.org/10.14716/ijtech.v15i1.5498
Nishiyama, Y 2017, 'Easy measurement system by using conventional echo sounder', In: The Asian Fisheries Acoustic Society (AFAS), Guangzhou, China
