Study on the Application of Model-based Control Algorithm for a Suspended Cable-Driven Parallel Robot

This paper introduces a model-based control scheme for controlling the position of a suspended cable-driven parallel robot. The robot is designed to have a fixed frame base with four cables. The cables are attached to winches on one end, driven by stepper motors, and to a moving platform at the other end. The control scheme consists of two systems: the reference model and the implemented control. The implemented control hosts the stepper motor to drive the winch based on the requirements derived from the reference model. The reference model converts the desired Cartesian trajectory into joint spaces, which are then translated into the number of required steps. The number of steps will act as a set point for the stepper motor. Three trajectories are generated to test the compliance of the controller with its position. The error compensation scheme is introduced to increase the positional accuracy of the previous controller, especially on the z-axis. This algorithm uses the nature of discrete stepper motor movement to estimate the actual cable length, which is then fed back to the control system as an error. The control simulation results indicate a significant improvement in control performance, i.e. reduced position error, was achieved.

Cable-Driven Parallel Robot (CDPR); Error compensation; Model-based control; Stepper motor

    Nowadays, many different types of robots are used in industries, for example, arm and gantry robots. However, the use of these robots frequently comes with a number of issues related to their movement. (Baskoro, Kurniawan and Haikal, 2019). A new type of parallel manipulator that has emerged since the 1980s is a Cable-Driven Parallel Robot (CDPR). CDPR is a new type of manipulator where the rigid links are replaced by cables, giving it numerous advantages. Cables can bear a higher payload (Qian et al., 2018) due to their ability to withstand high tension. Unlike rigid links, cables can be actuated by coiling and uncoiling, which does not take up space, expanding their workspace (Gosselin, 2013). Moreover, cables have lower inertia and can be driven at high speeds (Qian et al., 2018). Capabilities possessed by CDPR have been realized in several industrial applications, such as material handling in port logistics (Holland and Cannon, 2003), aircraft maintenance (Nguyen and Goutterfarde, 2014), offshore sandblasting (Gagliardini et al., 2014), structural painting (Nguyen et al., 2014), large scale construction (Hussein, Santos, and Gouttefarde, 2018), rescue operation (Daney and Merlet, 2010), etc. CDPR can also be introduced as an alternative technology for search-and-rescue operations since it can cover a wide range of areas and has a high payload-to-weight ratio (Nurahmi et al., 2017).
    Thus far, numerous topics related to CDPR, such as kinematics and path planning, have been extensively covered, but there is relatively limited information available on its control system. The control system of CDPR faces a significant challenge due to the flexible nature of cables, which can only exert force. Position of the moving platform is harder to control due to its flexibility, which leads to lower accuracy (Jung et al., 2016). The need to be in tension also implies that an under-constrained configuration cannot be fully controlled (Qian et al., 2018). A number of feedback control laws have been developed to tackle these issues, such as PD (Kawamura et al., 1995), Lyapunov-based and feedback linearization-based Proportional Derivative, PD (Alp and Agrawal, 2002), and Proportional Integral and Derivative, PID (Khosravi and Taghirad, 2014, Khosravi, Taghirad, and Oftadeh, 2013) to control the position of the end effector. However, the major drawback of these methods is that they do not consider the dynamics due to payload, thus leading to high position error. To solve this issue, more complex control has been introduced, such as sliding mode control (Hu et al., 2014), force control (Kraus et al., 2014), differential flatness (Yoon et al., 2018), and active stabilizer (Lesellier et al., 2018). Feed-forward compensators are also used for cable elasticity (Piao et al., 2017) and vibration reduction (Baklouti et al., 2019).

In this paper, a model-based control algorithm will be presented for the suspended cable robot. Due to CDPR's appealing advantages, such as large workspace and high load capacity, relatively lightweight, low cost, etc., CDPR has gained large attention from many applications. In this paper, the illustration of the cable robot and its use to aid search and rescue operations are shown in Figure 1. The robot is designed to move debris due to natural disasters, and therefore, it does not need to be in high precision. The term model-based refers to the use of an actuator model in the control algorithm. A Stepper motor is used to drive the cables, with a number of steps taken as a set point. The discrete nature of moving in steps is used as feedback to the system. Therefore, the cable lengths can be calculated by using the linear-angular relationship between cables and the stepper motor. Three trajectories are selected based on past work carried out (Syamlan et al., 2019, Syamlan et al., 2020). The desired and actual trajectories will be compared along with their error, and the result will be used to suggest an improvement. The structure of this paper is as follows: The mechanical modeling of the cable robot and the motor is shown in section 2. Section 3 describes three potential work trajectories, and Section 4 describes the controller design, which contains the suggested and enhanced control systems. The simulation results for both control strategies on the specified trajectories are shown in Section 5's results and discussions.

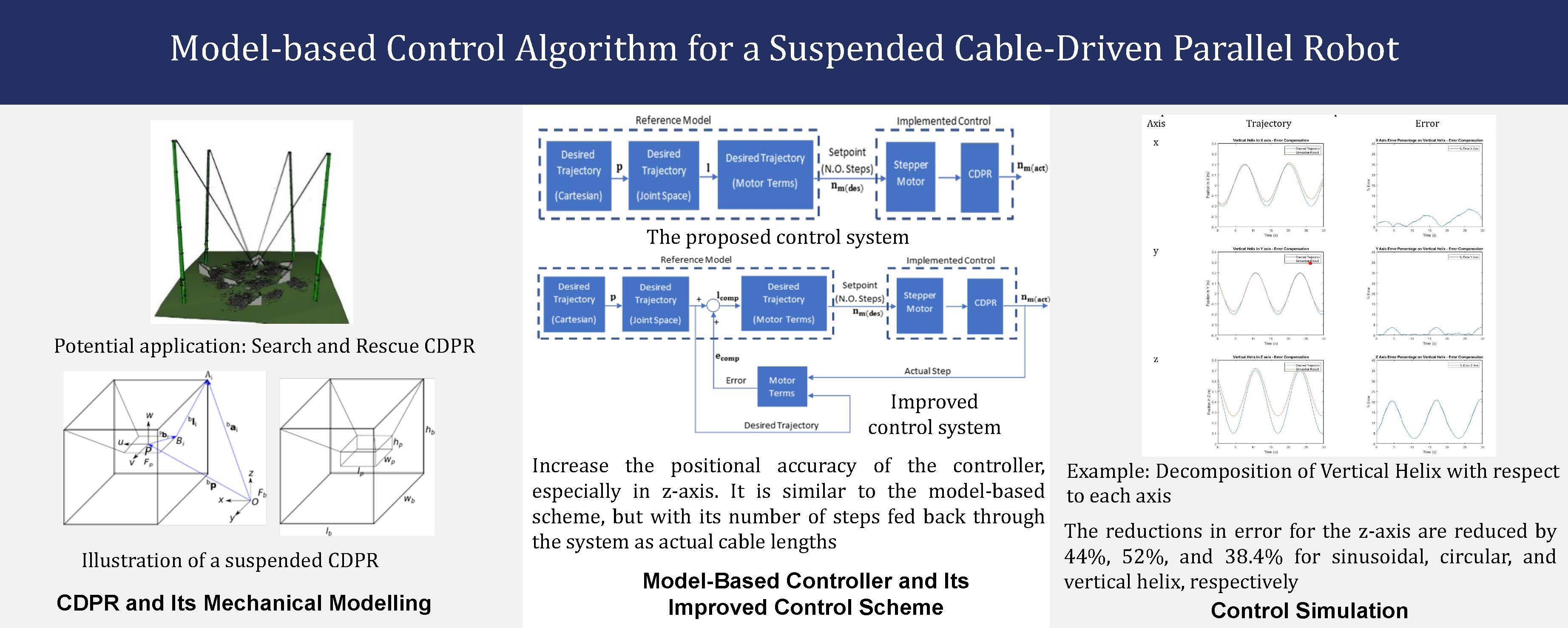
Figure 1 Illustration of Search – and – Rescue CDPR

Mechanical Modelling 

    The reference model consists of the inverse geometric model and the motor model. It converts the desired trajectory from Cartesian space into joint space. The trajectory serves as input for geometric analysis, carried out to convert the desired position into the desired cable lengths. It is then translated into the number of steps that have to be generated by the stepper motor by using the motor model. In general, the reference model hosts mechanical modeling of the whole system, from the robot model to its supporting mechanisms. The geometric analysis and the motor model will be discussed briefly in this section.
2.1. Geometric and Dynamic Analyses
    The suspended CDPR understudy comprises four cables, a cube moving platform, and a cube base frame, as shown in Figure 2. Each cable connects the cube-moving platform at the point  to the base frame via a reconfigurable pulley at the point , as shown in Figure 3. The moving platform is defined by length , width , and height , and the moving coordinate system . The geometric center P of the moving platform has its position coordinate expressed in the base frame denoted by . The origin of the base frame is denoted by point O. The base frame is situated on the bottom of the fixed frame, denoted by . The base frame is defined by length , width , and height . The pulley which can freely rotate about  axis of the angle  as depicted in Figure 3(b), is considered as a reconfiguration strategy. The pulley reconfiguration contributes to the robot motion and cable tension, as reported by (Syamlan et al., 2020).

    The point in the moving platform needs to be expressed with respect to the base coordinate system by introducing rotation matrix R. Suppose the rotations about  axes are denoted by . This is referred to as roll, pitch, and yaw, respectively. Then, the orientation of the moving frame with respect to the base frame can be expressed as:

Combining both the translational and rotational positions of the moving platform become:

                            

Each cable runs through a pulley, connecting the moving platform to the fixed frame. The cable end that is attached to the moving platform is referred to as anchor points , where . The position vector of these anchor points is expressed with respect to the platform frame , denoted as . Pulleys are attached to each side on the top of the fixed frame. The cable enters the pulley at the contact point  and exits at the point , as shown in Figure 3(a).  The position vector of these contact points is expressed with respect to the base frame , denoted as . The cable distance between the contact point and anchor point  is the cable length, denoted as . Therefore, by using loop closure, the vector of cable lengths can be determined as follows: 

                                    

For more detailed mathematical expressions of the reconfigurable pulley at the contact point , the readers may refer to (Syamlan et al., 2020).
The unit vector of cables is derived as:

Figure 2 Geometric representation of a suspended CDPR

Figure 3 Detailed description of a pulley mechanism
    The cable mass and stiffness are negligible since the cable is relatively lighter than the rigid links. The unit vector of the cable  is used to determine the wrench matrix . This matrix is useful to derive the dynamics of CDPR based on the Newton Law of motion, as follows:

Where  is the cable tension,  is the external wrench,  is the mass of the moving platform, and  is the acceleration of the moving platform. The trajectory generation discussed hereafter will provide the information corresponding to the position, velocity, and acceleration of the moving platform. Given the acceleration , the cable tension can be deduced from Equation (5). Since each cable is mounted to the winch and motor, the cable tension from Equation (5) can be used directly to compute the motor torque depending on the motor shaft diameter.

2.2. Motor Modelling

The cable lengths obtained from the geometric model need to be represented in terms of its actuators. In this case, stepper motors are used to drive the cables. Stepper motors are chosen because they move by number of steps, which is the multiplication of their step angle. Therefore, actual steps can be gathered without the need for an additional sensor. Before deriving this relationship, some assumptions are taken into account as follows:

1. Pulley and cables are assumed mass-less and friction between pulley and cables is assumed negligible.

2. Winches are assumed to always coil only one layer of cable.

3. Transmission loss within the actuator is assumed negligible.

4. No missed steps were generated by the stepper motor.

    The current control scheme applied to the robot focuses solely on position control. The rotation of the shaft angle acts as the set point to the control scheme. The stepper motor moves the shaft to the desired angle  determined by the number of steps  that must be generated according to its step angle , and mathematically can be expressed as:

                                

The relationship between the desired cable length  and the desired shaft angle can be written as:

where  defined the shaft radius. Hence, the number of steps required to generate the desired shaft angle based on the desired cable length can be mathematically expressed as:

                

Rearranging the equation to find a number of steps  gives:

    

Trajectory Generation

Three trajectories, namely sinusoidal, circular, and vertical helix trajectories, are generated in this paper based on (Gosselin, 2010). The design parameters of the CDPR model shown in Table 1 are referenced from previous work on the suspended CDPR conducted by (Syamlan, 2020). The results corresponding to the platform position between the desired values versus the actual one and its error will be presented for each trajectory.

Table 1 Design Parameters

3.1. Sinusoidal Trajectory
    The moving platform following the sinusoidal trajectory oscillates in the -axis. The moving platform position   expressed with respect to the base frame, has its oscillation frequency and amplitude of  respectively. The initial height of the platform is denoted as , which in this case is set to be equal to . The position can be expressed as:

            

    The velocities and accelerations are obtained by deriving Equation (10) with respect to time. The trajectory parameters for the sinusoidal wave used in this paper are based on (Syamlan, 2020), as shown in Table 2.
Table 2 Trajectory Parameters for the Sinusoidal Motion

3.2. Circular Trajectory
    The second trajectory generated in this paper is a circular trajectory lying on the xy-plane. The position of the moving platform tracing this trajectory is expressed with respect to the base frame. The initial height of the moving platform is denoted by . The rotating frequency and amplitude of the trajectory are defined as  respectively. The moving platform poses tracing this trajectory can be mathematically determined as:

By deriving Equation (11) with respect to time, the velocities and accelerations of the moving platform are determined. The parameters that are used to construct the circular trajectory are based on (Syamlan, 2020), as shown in Table 3.
Table 3 Trajectory Parameters for the Circular Trajectory

3.3. Vertical Helix
    The vertical helix trajectory is a more complex. The platform rotates with respect to the -axis with an amplitude of  while simultaneously performing an oscillation in the vertical direction. The frequencies for both the rotation and oscillation are denoted by respectively. The initial height of the platform is set as , which is equal to . The amplitude of oscillation is denoted by . The moving platform position executing the vertical helix trajectory can be mathematically defined as:

By performing the time derivative for Equation (12), the velocities and accelerations of point P can be defined. The values assigned to each parameter are based on (Syamlan, 2020), as summarized in Table 4.
Table 4 Trajectory Parameters for the Vertical Helix

Controller Design
4.1. Proposed Control Scheme
    The proposed control scheme comprised two sub-systems, a reference model and an implemented control. The reference model generates set points for the controller. It converts Cartesian trajectory into the required cable lengths for each motor. These values are then translated into equivalent shaft angles. A number of steps obtained from the shaft angle will be used as a set point for the Implemented control. The proposed block diagram of the system is shown in Figure 4.

Figure 4 Block Diagram of the Proposed Control Scheme.
Each cable will be driven by a Sumtor 57HS6425A4D8 stepper motor. The specification of the stepper motor is shown in Table 5.
Table 5 Motor Specification

4.2.  Improved Control Scheme
    The proposed control scheme is enhanced by the error compensation scheme. This control strategy was created to improve the controller's position precision, particularly on the z-axis. It is analogous to the model-based scheme, with its number of steps being fed back through the system as an actual cable length, as shown in Figure 5.

Figure 5 Block Diagram of Improved Control Scheme.
    Multiplying the number of steps by the shaft radius will give the actual cable length as follows:

                        

     Routing this value back and subtracting this value from the desired cable length will give a value that is like a position error. The error will be added to the system as an addition to determine the compensated length as follows:

                            

    The difference between the actual and desired cable length is defined as error _comp, which can be mathematically expressed as follows:

                        

    This improved control scheme is applied to the CDPR understudy such that the motion of the moving platform will follow as close as possible to the generated trajectory. The results are presented and discussed hereafter.

 

Figure 7 Errors from Sinusoidal Motion (a) Model-based control, (b) Error compensation control.

Figure 8 Results from Circular Horizontal Motion (a) Model-based control, (b) Error compensation control.

Table 6 Decomposition of Circular Trajectory with respect to each axis.

Figure 9 Results from Vertical Helix Motion (a) Model-based control, (b) Error compensation control.

Figure 9(a) presents a comparison between the desired and actual trajectories for the vertical helix achieved through model-based control. It is noteworthy that the actual trajectory exhibits a smaller radius and higher position in comparison to the desired trajectory. Overall, it is observed that the actuator is able to track the set point in less than 5 seconds. There is a slight difference between the desired and the actual pose in the x and y axis, but in general, the y-axis performs better than the x-axis. In terms of error, the overall error is less than 5% and 5.5% for both axes, respectively. As for the z-axis, the major difference is seen between the desired and the actual pose, with errors as high as 32.8%. Based on these results, it can be concluded that, in general, the control scheme performs well on the x and y-axis but not on the z-axis. Therefore, an improvement termed an error compensation control scheme was proposed. Significant improvement is seen in the vertical helix when using an error compensation scheme, as shown in Figure 9(b). The circular radius becomes wider, and the robot is now able to follow the z-axis trajectory. The trajectory for each axis is summarized in Table 9. Using the error compensation scheme reduces the error on y-axis by 26%, but a slight increase of 29% to 7.1% for the x-axis. The error reduction is also seen on the z-axis of the vertical helix at 38.4%, from 32.5% to 20.5%. The highest error is still registered at the downward motion, especially in the lowest position.

A control scheme and its improvement for suspended cable-driven parallel robots have been developed, namely model-based and error compensation control. The robot is designed to have a fixed frame base with four cables. The cables are attached to winches at one end, which are driven by stepper motors, and a moving platform at the other end. Both control schemes consist of two systems, namely the reference model and the implemented control. The main difference between the model-based and error compensation control is that the latter uses the nature of the stepper motor to acquire the actual cable length without the need to use sensors. The actual cable length is fed back into the system as an error. Both schemes are tested on three trajectories, sinusoidal, circular, and vertical helix. In general, the model-based control scheme has reduced performance in z-axis, with errors as high as 32.5% when performing the vertical helix. The error compensation scheme shows better control performance as compared to the model-based ones, reducing errors for all trajectories noticeably in the z-axis. The reduction in error for z-axis is reduced by 44%, 52%, and 38.4% for sinusoidal, circular, and vertical helix, respectively.

        This work is supported by the Ministry of Research and Higher Education of Indonesia, under the scheme of Fundamental Research 2019, No. T/208/IT2.VII/HK.00.02/xi/2019. 

Alp, A.B., Agrawal, S.K., 2002. Cable Suspended Robots: Feedback Controllers with Positive Inputs. In: Proceedings of American Control Conference, Volume 1, pp. 815–820

Baklouti, S., Courteille, E., Lemoine, P., Caro, S., 2019. Vibration Reduction of Cable-Driven Parallel Robots through Elastodynamic Model-Based Control. Mechanism and Machine Theory, Volume 139, pp. 329–345

Baskoro, A.S., Kurniawan, R.P., Haikal, 2019. Evaluation of the 2-Axis Movement of A 5-Axis Gantry Robot for Welding Applications. International Journal of Technology, Volume 10(5), pp. 1024–1032

Berawi, M.A., Leviakangas, P., Muhammad, F., Sari, Gunawan, Yatmo, Y. A., Suryanegara, M., 2019. Optimizing Search and Rescue Personnel Allocation in Disaster Emergency Response Using Fuzzy Logic. International Journal of Technology, Volume 10(7), pp. 1416–1426

Berawi, M.A., 2021. Philosiphy of Technology Design: Creating Innovation and Added Value. Internation Journal of Technology, Volume 12(3), pp. 444–447

Daney, D., Merlet, J.P., 2010. A Portable, Modular Parallel Wire Crane for Rescue Operations. In: 2010 IEEE International Conference on Robotics and Automation, pp. 2834–2839

Gagliardini, L., Caro, S., Gouttefarde, M., Wenger, P., Girin, A., 2014. Optimal Design of Cable-Driven Parallel Robots for Large Industrial Structures. In: IEEE International Conference on Robotics and Automation (ICRA), pp. 5744–5749

Gosselin, C., 2013. Cable-Driven Parallel Mechanism: State of the Art. Bulletion of JSME

Gosselin, C.M., 2010. Global Planning of Dynamically Feasible Trajectories for Three-DOF Spatial Cable Suspended Parallel Robots. Mechanisms and Machine Science, Volume 12, pp. 3–22

Holland, C.S., Cannon, D.J., 2003. Cable Array Robot for Material Handling. USA: United States Patent. US6826452B1

Hu, Y., Tao, L., Jia, J., Lv, W., 2014. Control and Simulation of Cable-Driven Parallel Robots in Offshore Cargo Handling. In: Proceeding of the 11^th World Congress on Intelligent Control and Automation, pp. 2451–2455

Hussein, H., Santos, J.C., Gouttefarde, M., 2018. Geometric Optimization of a Large Scale CDPR Operating on a Building Façade. In: International Conference on Intelligent Robots and Systems (IROS), pp. 5117–5124

Jung, J., Piao, J., Park, S., Park, J.-O., Ko, S.Y., 2016. Analysis of Cable Tension of High-Speed Parallel Cable Ro-bot: High Speed Position Tracking of Winch. In: 16^th International Conference on Control. Automation and Systems (ICCAS), pp. 1053–1056

Kawamura, S., Choe, W., Tanaka, S., Pandian, S.R., 1995. Development of an Ultrahigh Speed Robot FALCON Using Wire Drive System. In: Proceedings of IEEE International Conference on Robotics and Automation, Volume 1, pp. 215–220

Khosravi, A.M., Taghirad, H.D., 2014. Robust PID Control of Fully Constrained Cable Driven Parallel Robots. Mechatronics, Volume 24(2), pp. 87-97

Khosravi, A.M., Taghirad, H.D., Oftadeh, R., 2013. A Positive Tensions PID Controller for a Planar Cable Robot: An Experimental Study. In: First RSI/ISM International Conference on Robotics and Mechatronics (ICRoM), Tehran, pp. 325–330

Kraus, W., Schmidt, V., Rajendra, P., Pott, A., 2014. System Identification and Cable Force Control for a Cable Driven Parallel Robot with Industrial Servo Drives. In: 2014 IEEE International Conference on Robotics and Automation (ICRA), pp. 5921–5926

Lesellier, M., Cuvillon, L., Gangloff, J., Gouttefarde, M., 2018. An Active Stabilizer for Cable-Driven Parallel Robot Vibration Damping. In: 2018 IEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, pp. 5063–5070

Nguyen, D.Q., Gouttefarde, M., Company, O., Pierrot, F., 2014. On the Analysis of Large-Dimension Reconfigurable Suspended Cable-Driven Parallel Robots. In: 2014 IEEE International Conference on Robotics and Automation (ICRA), pp. 5728–5735

Nurahmi, L., Pramujati, B., Caro, S., Jeffrey, 2017. Dimension Synthesis of Suspended Eight Cables-Driven Parallel Robot for Search-and-Rescue Operation. In: 2017 International Conference on Advanced Mechatronics, Intelligent Manufacture, and Industrial Automation (ICAMIMIA), pp. 237–241

Piao, J., Jin, X., Jung, J., Choi, E., Park, J.-O., Kim, C.-S., 2017. Open-Loop Position Control of a Polymer Cable–Driven Parallel Robot via a Viscoelastic Cable Model for High Payload Workspaces. Advances in Mechanical Engineering. Volume 9(12), pp. 1–12

Qian, S., Zi, B., Shang, W.-W., Xu, Q.-S., 2018. A Review on Cable-driven Parallel Robots. Chinese Journal of Mechanical, Volume 31(1), pp. 1–11

Nguyen, D.Q., Goutterfarde, M., 2014. Study of Reconfigurable Suspended Cable—Driven Parallel Robots for Airplane Maintenance. In: IEEE International Conference on Intelligent Robots and System, pp. 1682–1689

Syamlan, A.T., Nurahmi, L., Pramujati, B., Tamara, M.N., 2019. Dynamic Trajectory Generation of Suspended Cable-Driven Parallel Robot. In: AIP Conference Proceedings, Volume 2187(1), p. 050006

Syamlan, A.T., Nurahmi, L., Tamara, M.N., Pramujati, B., 2020. Dynamic Trajectory Planning of Reconfigurable Suspended Cable Robot. International Journal of Dynamics and Control, Volume 8, pp. 887–897

Syamlan, A.T., 2020. Mechanical Modelling and Control of Suspended Cable Driven Parallel Robot (CDPR) for Search and Rescue Operation. Master Thesis, Graduate Program, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia

Yoon, J., Hwang, S.W., Bak, J.-H., Park, J.H., 2018. Vibration Suppression of CDPRs Based on Differential Flatness. In: IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, pp. 259–264