Modeling of Ship Sailing Patterns in Maluku to Support the Sea Highway
Corresponding email: macs_tukan@fatek.unpatti.ac.id
Published at : 25 Jan 2024
Volume : IJtech
Vol 15, No 1 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i1.6231
Tukan, M., Esmail, H.A.H., Hozairi, Camerling, B., Alim, S., Manapa, E.S., Berhitu, P., 2024. Modeling of Ship Sailing Patterns in Maluku to Support the Sea Highway. International Journal of Technology. Volume 15(1), pp. 166-178
| Marcus Tukan | Department of Industrial Engineering, Faculty of Engineering, Pattimura University, Kampus Poka, Ambon, 97233, Indonesia |
| Hanaa Abdelaty Hasan Esmail | Commerce Department, Economic, Port Said University, 42526, Egypt |
| Hozairi | Department Informatics Engineering, Faculty of Engineering, Madura Islamic University, Pamekasan, 69351, Indonesia |
| Billy Camerling | Department of Industrial Engineering, Faculty of Engineering, Pattimura University, Kampus Poka, Ambon, 97233, Indonesia |
| Syariful Alim | Department Informatics Engineering, Faculty of Engineering, Bayangkara University, Surabaya, 60231, Indonesia |
| Esther Sanda Manapa | Graduate School Department of Transportation, Naval Engineering, Hasanuddin University, Makasar, 90245, Indonesia |
| Pieter Berhitu | Departement Urban and Regional Planning, Coastal Management, Faculty of Engineering, Pattimura University, Kampus Poka, Ambon, 97233, Indonesia |
The low level of the ships' load factor (LF) in
the Maluku archipelago region can be attributed to the lack of compatibility
between ship loads and the available cargo potential in the region. Therefore,
the implementation of an optimal sailing pattern is required. The sailing
pattern of the ship can be optimal if it can carry cargo according to the
available potential because this circumstance can improve sailing efficiency.
The purpose of this study is to determine the optimal sailing pattern according
to the potential of the Maluku region to support the maritime highway program
in Maluku. Firstly, Fuzzy Multi-Attribute Decision Making (Fuzzy MADM) was used
to determine the optimal model of ship operating patterns in the Maluku archipelago
region. Secondly, a time series correlation analysis was conducted to identify
patterns and correlations among the data. This analysis provides insights into
the relationships between different variables over time. Thirdly, another
analysis was performed using the Cobb-Douglas production theory to identify the
influencing variables on the number of ship visits (Call), ship deadweight
tonnage (DWT), and ship cargo potential (QS). The results show that
the selection of the best ship operating pattern using the recommended Fuzzy
MADM method is a mixed sailing pattern, namely regular and tramper sailing. In
addition, increasing the productivity of QS_R+T and DWT ships will
have a positive effect on ship visits in a certain time unit. If the potential growth
of positive cargo QS_R+T > Call and DWT, then it is important to
build new ships with optimal DWT so as to increase ship efficiency in
supporting the maritime highway program. This research provides a significant
contribution to the development of an efficient and sustainable national
logistics system, as well as being a policy reference for decision-making
related to the sailing pattern and the development of the maritime highway
program in Maluku.
Archipelago; Fuzzy MADM; Maritime highway; Sailing patterns
The
geographical condition of an area greatly influences the development of
transportation and tends to be influenced by the characteristics of differences
in potential natural resources, human resources, and the availability of
existing infrastructure. This condition
requires a different development approach for each island region, especially in
the Maluku region. However, sea transportation infrastructure, such as ships,
ports, networks, and ship operating patterns, must be developed synergistically
as the main support for regional development in order to provide optimal
services (Tukan
et al., 2015).
Efficiency is a key condition in operating ships, both passenger ships and
cargo ships. Therefore, efficiency becomes the goal of planning the island’s
transportation system to support the maritime highway service network (Nurkholis
et al., 2016).
The operational cycle of sea transportation is determined
by the availability of the cargo to be transported, the shipping network and
ships, as well as adequate port infrastructure. If one of the parameters does
not work optimally, it will have an impact on decreasing other operational
performance, so it can be described as a multiplier effect of sea
transportation (Tukan et al., 2012), (Jaal and Abdullah, 2012). Transportation has a strong positive
influence on economic development, and increased production can be directly
related to increased transportation (Tukan, 2021).
The regular shipping pattern consists of fixed routes and
schedules which are very suitable for industrial areas with stable production
schedules and cargo quotas. Meanwhile, shipping patterns with irregular routes
or based on certain port points to other port points are usually applied to
non-container route ships that are always changing. Therefore, a mixed shipping
pattern between Regular and Tramper can increase the amount of cargo carried.
From the results of observations, differences were found in shipping patterns
in the archipelago. Therefore, the purpose of this research is to evaluate the
efficiency of shipping patterns in Maluku to support the maritime highway
policy in Indonesia.
Figure 1
Voyage Pattern of Ships in Maluku
In this study, the pattern of sailing in
the island region of Maluku Province can be seen in Figure 1. The illustration
in Figure 1 shows that the port of Luhu, Loki port, and Piru port to Hitu port
is carried out regularly. On the other hand, at Saparua port, Amahai port,
Tehoru port, to Tulehu port, sailing is carried out in combination between
regular and tramper. Therefore, it is necessary to analyze the feasibility of the region's economic
potential to ensure the most efficient industrial policy (Zhogova, Zaborovskaia, and Nadezhina, 2020)
so that
it can also be carried out on industrial shipping, also the importance of
interaction between island regions to drive regional economic growth (Kozonogova, Dubrovskaya, and Dubolazova, 2020).
The
transportation network has a positive causal effect on the rate of per capita
growth in all sectors. Therefore, the availability of infrastructure must have
a significant impact on the performance of the transportation network and
changes in economic behavior. This argument relies on the simple logic that individuals
first need to have access to transportation in order to benefit from it (Banerjee, Duflo,
and Qian, 2020). The maritime infrastructure
approach model can be used to measure economic growth with infrastructure
improvements that can ensure loading and unloading operations, reduce port
operating costs and increase product competitiveness on the island (Tukan et al.,
2015). Thus, it can be said that the maritime sector is an
important economic route. It is also considered a window to support trade and
attract investment (Esmail, 2016).
All the above explanations, of course, must be supported by a good ship
sailing pattern.
The
hypothesis in this study found that there is a relationship between sailing
patterns and ship efficiency, so this study will identify the parameters of
sailing patterns and ship operating efficiency in typical island areas. By
taking the port of Hitu, Luhu port, Loki port and Piru port as well as Saparua
port, Amahai port, Tehoru port and Tulehu port, as examples of cases where the
correlation between dimensions of sea transport and ship sailing patterns, dead
weight tonnage (DWT), number of visits ship (Call) per unit time and potential
shipload (QS) have an impact on the operational efficiency of ships
on an island.
In
general, the operation of ships on small islands has its own unique
characteristics. Some operations are carried out regularly, while others are
conducted through trampers, or sometimes a combination of both regular and
tramp services. Therefore, in this research, a study on the modeling of ship
sailing patterns at of ports will be carried out to support Indonesia's maritime
highway policy. Determination of ship operations will be selected based on four
criteria, namely cargo depending on seasonal factors (Cr1), industrial product
cargo (Cr2), annual average shipload above 60% (Cr3), and ship visits per unit
time (Cr4). Therefore, determining the pattern of ship operation in these small
islands is a complex problem, so it is necessary to develop a decision support
system that will provide the best decision solution based on the consideration
of several predetermined criteria.
Based
on previous research related to multi-criteria decision-making, many
researchers have done this, as was done by (Lumaksono,
2018) for
selecting suitable fishing gear for fishermen on Madura Island using Fuzzy AHP
and Fuzzy TOPSIS. (Hozairi
et al., 2019) Regarding
the study of the most influential factors on Indonesian maritime security using
the Fuzzy Analytical Hierarchy Process. (Tukan
et al., 2020)
regarding a decision support system for determining the location of floating
docks in the Maluku Islands using AHP-TOPSIS. (Amelia, Lathifah, and Yasa, 2021; Santos, Portugal, and Ribeiro, 2021) on evaluating the performance of highway concessions through
public-private partnerships using a fuzzy multi-criteria decision-making
procedure. (Xu
et al., 2022), (Goodarzi, Abdollahzadeh, and Zeinalnezhad, 2022)
on risk assessment for environmentally friendly integrated energy systems using
Fuzzy MCDM. This problem can be solved by combining the multi-criteria
decision-making method and an intelligent system, namely Fuzzy SAW. Based on
previous research studies on the application of the Fuzzy-SAW method to solve
complex problems to determine the most influential criteria and the most
appropriate decision alternatives, so that in the problem of determining ship
operating patterns in the small islands, the Fuzzy-SAW method is chosen as a
tool for resolve decision-making problems related to the assessment of ship
operating models in existing archipelagic areas. For this reason, a sailing pattern is needed
that can increase the load factor (LF) and sailing efficiency on small islands.
(Wang
and Wang, 2011) concluding
in the future how shipping companies form global sailing networks.
The research methodology consists of three
steps. The first step is to analyze sailing patterns in archipelago ports to
support maritime highway policy using Fuzzy-SAW. The second step is to analyze
the correlation between the increase in the number of ship calls (Call) and
deadweight tonnage (DWT), potential ship loading (QS) using time
series methods. The final step is to analyze the performance of the ship's
sailing pattern using the Cobb-Douglass production theory.
The operation of ships on
small islands is characterized by its unique attributes. Some operations occur
on a regular basis, while others utilize trampers. Alternatively, a combination
of regular services and trampers is implemented. Regular patterns often occur
in large island areas where goods are produced from industrial products and are
carried out routinely and on a scheduled basis (such as on the large island of
Java). Meanwhile, the tramper pattern only occurs in island areas (such as the
Maluku Islands) where production results come from the traditional
agricultural, plantation and livestock sectors where the results are more
influenced by seasons or natural factors (Tukan,
2021). This problem can be described as a causal relationship between
shipping patterns and cargo availability which can be modeled as shown in
Figure 2.
Figure 2 Efficiency Model of
Sailing Patterns in the Island Region
The efficiency of
sailing (? sailing) is determined by the size of the potential area and the potential
for cargo that is in synergy with the ship's DWT and ship's Call. From this
point, the ship pattern is determined as more efficient in terms of operation
and optimal related to income to ensure the continuity of ship operations. For
this reason, the ship pattern can be chosen whether the ship operates with a
regular ship pattern, tramper and a combination of regular and tramper. While
choosing a ship pattern, the Fuzzy-SAW method can be implemented.
2.1. Modelling
of ship operation patterns using Fuzzy MADM
More
efficient and optimal modeling of sailing
patterns can be obtained using the fuzzy method, where the information is full
of uncertainty. However, through such a method, fuzzy numbers can employ
arithmetical operations (Kumar, Maheshwari,
and Sharma, 2015). The basic concept of a fuzzy decision
support system is rooted in the relationship between elements within the
system, which is represented as a set that captures the relationship between
two or more sets, where the ship's operating pattern is determined by the availability of
cargo. It can be done using a multi-attribute decision making (MADM) approach
by evaluating alternatives m Ai (i = 1,2,..n) in which each criterion is Cj (j
= 1, 2,… n) and each attribute is independent of one another. The decision matrix for each
alternative especially for the attribute X = attribute for the ship's operating
pattern is described in equation 1.
where Xij is the ith
performance rating on attribute j. The weight value shows the level of
importance relative to the attribute, which is described as W as shown in
equation 2.
Where the pattern of shipping efficiency is determined
by the load factor (LF) of the ship in relation to the cargo being transported.
If LF < 60, then the ship will lose money. Moreover, it will not be able to
bear its operational costs. For this reason, an alternative optimal sailing pattern is sought. The optimal sailing pattern is the number of ship visits
(Call) required for cargo per unit time with LF > 60% (Tukan et al.,
2012).
Ship
operation decision-making in which preference information about alternatives
provided by the decision maker is represented in two different formats, namely
multiplication preference relationship and fuzzy preference relationship, in
order to minimize the gap between collective opinion and preference
relationship. The opinions of each decision maker were used to integrate the
two different formats of preference relationships and to calculate the
collective rating scores of the alternatives. Thus the ranking of the most
desirable alternative or alternative (X) is obtained directly from the
calculated collective ranking value. Next, numerical examples are also used to
illustrate the application of the proposed approach.
Performance
rating (X) and weighted score (W) are the main values ??representing an
absolute preference for decision-making. The ranking process is carried out by
using multi attributes decision-making (MADM) to obtain the best-obtained
alternative based on the overall preferences given. Simple Additive Weighting (SAW) is one
of the methods in MADM that is used to normalize the decision matrix (X) to a
scale that can be compared with all available alternative ratings associated
with equation 3.
Where
rij = Normalized performance rating of the Ai
alternatives on the attribute Cj; i = 1, 2,…m and j = 1, 2,…m.
Equation 3 in this study focuses more on the cost attribute. Then the
preference value for each alternative V is given as following equation 4.
A
larger Vi value indicates that the alternative Ai is
preferred. In this study, the ship's operating pattern was selected, where A1 =
Regular pattern, A2 = Tramper pattern, A3 = Mixed pattern, and + tramper
pattern. The suitability rating of each alternative depends on the level of
importance of each criterion assessed with a weight of 1 to 5. Where in this
study, 4 criteria were chosen as decision-making materials, including Cr1=
cargo that depends on seasonal factors. In the case of a bountiful harvest season, the assigned weights for
different harvest conditions are as follows: a weight of 5 for abundant
harvests, a weight of 4 for sufficient harvests, a weight of 3 for moderate
harvests, a weight of 2 for less substantial harvests, and a weight of 1 for
very poor harvests. For Cr2 = cargo of industrial products, if the resulting
production takes place continuously, it gets a weight of 5, moderate production
weighs 4, moderate production weighs 3, very poor production weighs 2, and the
production is very underweight 1. Cr3= shipload per year on average above 60 %.
If LF of ship > 80 % by weight 5, LF of ship >70% and <79.9% by weight
4, LF of ship >60 % and < 69.9 % by weight 3, LF of ship > 50 % and
< 59.9 % by weight 2, LF ship <50% weight 1. Lastly, about Cr4 = ship
visits (Call) per unit time, if ship visits occur every week, a weight of 5,
ship visits every month weights 4, ship visits every 3 months weight 3, ship
visits every 5 months get a weight of 2, ship visits every 6 months weights 1. The suitability rating of each
alternative on each criterion can be followed in Table 1 below.
Table 1 The suitability rating of each alternative on each
criterion.
|
Alternatif |
Cr.1 |
Cr.2 |
Cr.3 |
Cr.4 |
|
The Reguler |
3 |
4 |
2 |
2 |
|
Tramper |
3 |
3 |
3 |
3 |
|
Reguler+Tramper |
5 |
5 |
4 |
4 |
Each value given to each alternative for
each criterion is a suitability value according to the weight of its importance
so that each given criterion is assumed to be the best criterion. The
results of the assessment by experts who are experienced in managing sailing
management give preference weights as W = (4, 4, 5, 3). So for that, we can
create a match matrix and table as follows:
The first
step is to normalize the X matrix based on equation 3. The following results
are obtained, as in Table 2 below.
Table 2 The results of the normalization of the X matrix are based on
equation 3
From Table 2, the normalized matrix R is obtained as follows
By
using equation (4), the V value is obtained as follows:
V1 = (4).(0,60) + (4).(0,60) + (5).(1,00)
= 9,80,
V2 = (4).(0,80) + (4).(0,60) + (5).(1,00) = 10,60,
V3 = (4).(1,00) + (4).(1,00) + (5).(1,00) = 13,00
From the results of calculations using the
Simple Additive Weighting (SAW) method, the value of V3 = 13 is the highest,
indicating that the ship's operating pattern is suitable for archipelagic areas
where production factors tend to come from natural sources such as the
agricultural, plantation, forestry, and fisheries sectors. These tend to be
influenced by the seasons so the optimal sailing pattern is a sailing pattern
that combines a regular sailing pattern and a tramper sailing pattern.
2.2. Ship
Visits, Ship Size and Cargo Volume
There
is a strong correlation between the increase in the number of ship visits
(Call), ship size (DWT) and cargo growth (QS), where the
greater volume of cargo will have an impact on ship visits and ship size in an
area, (Tukan et al., 2015). From
statistical data, the increase in the number of ship visits and ship size on
cargo growth can be analyzed using econometric methods. The availability of
shipload volume described as potential shipload (QS) is able to
increase the number of ship visits (Call) and ship size (DWT), and can be
modeled as equation (5).
Therefore, the optimization method
can be employed to calculate the availability of maximum QS cargo,
as well as the number of ship visits (Call) and the load capacity (DWT). The following equation (6) can be written to
explain it.
Goal :
To find the most influential sailing parameters that
can provide
efficiency to the operational performance of the ship, with the question of how
far these variables influence each other.
Variable:
X1 = number
of ship visits (Call),
X2 = ship
load capacity (DWT),
X3
= the amount of cargo on the ship (QS).
Constraint:
If QS ? Call and DWT where Call and DWT are
the maximum dimensions in one year, it can be ascertained that the ship's sailing operation is inefficient (LF<60).
However, the availability of cargo in an area is largely determined by the
production function that is carried out, whether it comes from industries that
can guarantee the availability (quota) and continuity of production or
agricultural, plantation and fishery products which are more influenced by
natural factors and season. Then the availability of charge shows a non-linear
production function. It becomes the linear function through a logarithmic
transformation. Therefore, the Cobb-Douglas function becomes equation 7.
Where the regression coefficient is the quantity
of load production elasticity, namely the percentage change in output as a
result of a one percent change in input o and
1,
2, ….
n referred to as Call and DWT parameters.
o is the intercept
when the value X1 equals zero.
1,
2,
….
n is also known as the slope. Slope states how much
the Call changes (
1), and DWT (
2), during the load growth rate changes by one unit. In economic mathematics, the
amount of elasticity can be obtained by the following equation 9.
APxi is the average product for
the input x (QS) which is obtained by the following equation
(10).
Thus the equation for loading and unloading
elasticity for input x (QS) is formed as following equation 11.
If in a loading and unloading process at the
port: where is the output (Y) = QS, an area of unity time (ton), and input (Xi) = a
number of the unit time ship visits (Call), so that it is able to carry out a certain
amount of cargo per unit time, a ship with a certain carrying capacity (DWT) is
needed.
Partially, all variables have a significant
effect on economic growth. For every one percent increase in cargo volume (QS),
ceteris paribus can encourage the growth of ship visits (Call) which can be
modeled as depicted in equation 12.
Here
the increase in QS also has a strong correlation with the increase
in shipload capacity (DWT), which can be modeled equation 13.
The increase in ship
loading capacity (DWT) affects the amount of cargo availability (QS)
of goods, which can be modeled into equation 14.
Where the Cobb-Douglas production function
can be employed to determine the global optimum in selecting the best model for
the development of potential cargo in an island area, taking into account
transportation dimensions such as Call and DWT, these factors play a crucial
role in determining the sailing pattern of ships in small islands.
2.3. Model
Analysis
Analysis
of sailing patterns using
production theory where the sailing
performance time series data shown in Figure 3.
Figure 3 Phase Diagram Analysis
The
number of ship visits (Call), ship capacity (DWT) and potential payload (QS)
are inputs that are processed in the form of multilinear regression and then
converted into Cobb Douglas form. This step is an input to find the maximum QS
condition with minimum Call and DWT. It is also necessary to find the optimal
solution for selecting ship sailing patterns with Fuzzy MADM. The above steps
are carried out to obtain optimal shipping conditions according to the
potentially available shiploads. To calculate the QS and the number
of call ships needed in a certain period of time and also a certain DWT can be
done by using a regression model that is modified on the Cobb Douglass
production theory model. The results of the analysis using the two methods
above can determine the appropriate shipping pattern for the island region.
2.4. Data
This study uses port
performance data (QS, Call, DWT) on conditions of sailing that are carried out
regularly or combined regular pattern + tramper pattern in the 2011-2021 period in the Maluku
archipelago, as shown in Table 3.
Table 3 Transport performance
data of ports in Ambon Island
|
Year |
Reguler Pattern |
Reguler + Tramper Pattern Mix | ||||
|
(Hitu Port specific data: Luhu, Loki, Piru) |
(Tulehu Port specific data: Saparua, Amahai, Tehoru) | |||||
|
QS |
Call |
DWT |
QS_R+T |
Call |
DWT | |
|
2011 |
2.111 |
737 |
11.876 |
23.664 |
728 |
21.840 |
|
2012 |
2.260 |
749 |
12.090 |
29.680 |
742 |
22.260 |
|
2013 |
2.733 |
777 |
12.268 |
33.840 |
750 |
24.064 |
|
2014 |
2.738 |
786 |
12.360 |
38.808 |
792 |
25.344 |
|
2015 |
4.370 |
1.031 |
19.471 |
52.624 |
1.012 |
35.420 |
|
2016* |
4.406 |
1.002 |
19.750 |
52.702 |
1.023 |
35.455 |
|
2017* |
4.392 |
1.042 |
19.752 |
54.801 |
1.037 |
35.560 |
|
2018* |
4.405 |
1.048 |
19.760 |
55.014 |
1.052 |
37.002 |
|
2019* |
4.762 |
1.062 |
19.802 |
57.021 |
1.074 |
37.105 |
|
2020* |
4.980 |
1.095 |
19.895 |
57.132 |
1.098 |
37.252 |
|
2021* |
4.810 |
1.071 |
19.826 |
57.094 |
1.076 |
37.194 |
Source: Ministry of Transportation RI
Hitu Port RIP document 2016. and *additional data on institutional
research at Pattimura University in 2022, which
was re-analyzed.
Results in the growth of
cargo, visits and ship capacity that continues to increase every year, analysis
of quantitative approaches in answering regional connectivity and efficiency of
sailing patterns in supporting the Sea Tol
is an illustration of the sailing
performance of the Maluku islands at a low-efficiency level, where many
shipping companies have to sail by looking for cargo so that there are areas
that are not served because ships are not visited. This makes it difficult for
the community to bring agricultural, plantation, forestry and fishery products
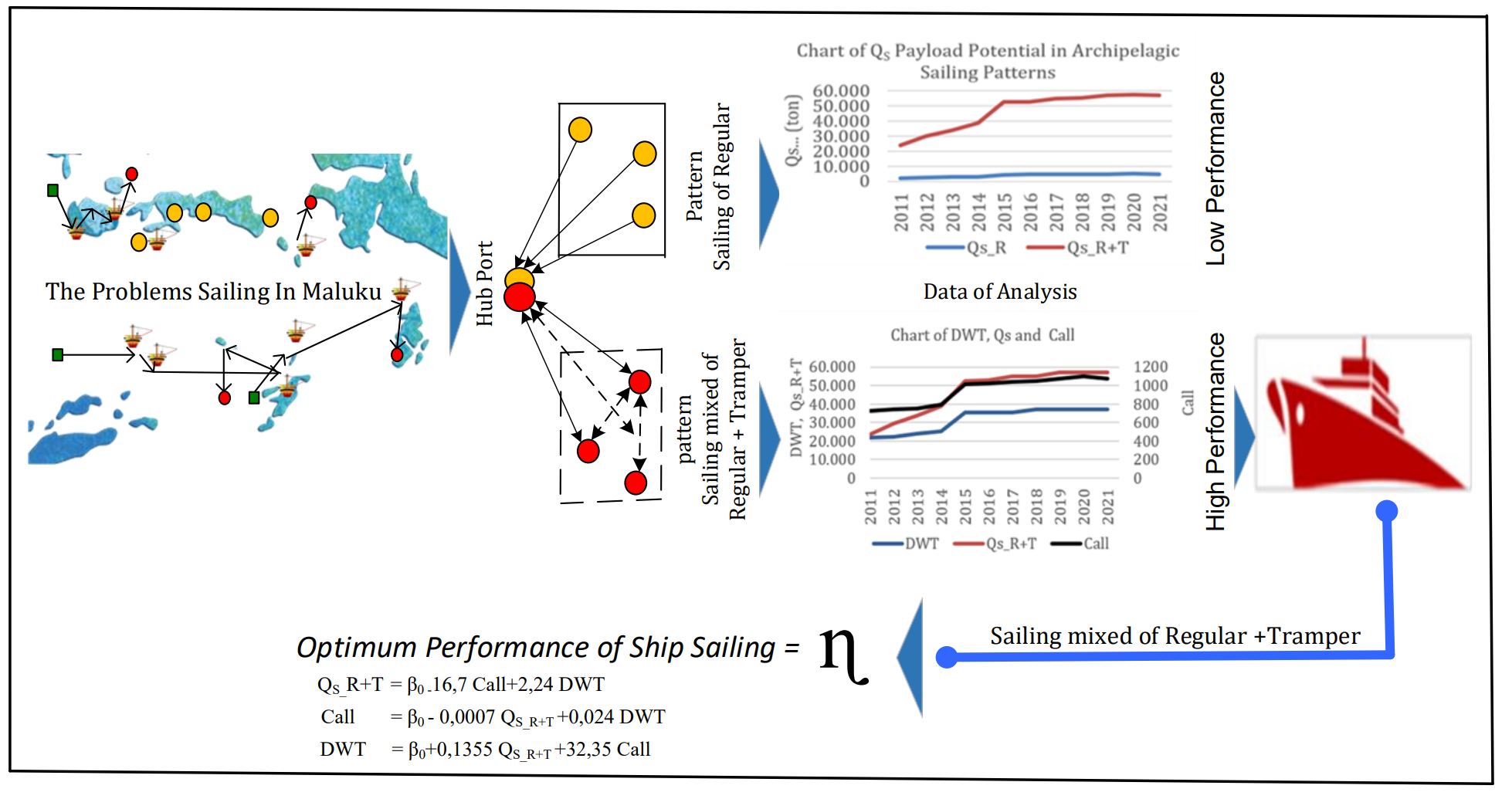
to be marketed. The pattern of regular sailing at the sample port shows an average growth over the last 11 (eleven) years, including: for Call = 0.041%/year,
DWT = 0.061%/year and cargo QS_R
= 0.116% /year. Meanwhile,
the mixed regular+tramper sailing
pattern at the sample port shows an average growth of 5 (five) years higher
than the regular or tramper pattern. For Call = 0.043%/year and DWT = 0.064%/year,
it expenses QS_R+T = 0.128%/year.
From
the description of the sailing pattern above, it can be seen as described in
Figure 4 below, where the amount of cargo carried QS_R+T is
higher than the usual QS_R
sailing pattern.
Figure 4
Differences in QS Payload Potential in Archipelagic Sailing Patterns
Figure 5 Archipelagic Sailing Pattern Performance
Analysis of the
selected sailing pattern is a
mixed sailing pattern where on
average, there are 3 (three) ships docked at the port (Tulehu Port, Saparua
Port, Amahai Port, Tehoru Port). The average size is 35 DWT, with an average
payload of 17,687 tonnes/call/port. Figure 5 shows the trend of sailing performance at several ports in the
Maluku islands and depicts an
insignificant increase. However, the
launch of the maritime
highway and connectivity by the Indonesian government in 2015 caused a
significant increase in 2014–2015. The graph of cargo growth on a mixed pattern QS_R+T continues to increase the average number of ship visits per
year, fulfilling the need for additional capacity and a number of ships to
support the maritime
highway.
The results of the analysis
between parameters of shipping performance can be seen in Table 4 using Minitab
19. In this table, R2 is the correlation coefficient which shows how
strong the relationship between parameters is, while ?0 is the intercept or
constant coefficient.
From Table 4, it can be
explained from the related parameters that for Call versus QS_R+T
and DWT, the parameters are known as ?o=207.1, ?1=0.0007 and ?2 = 0.024. It means that the growth of QS_R+T
and DWT have a positive effect on Call, and if there is a constant ceteris paribus ,.
Then a growth of 1% for QS. The DWT will have an impact on changes in
Call of QS_R+T = 0.001% as well as DWT = 0.024%.
Table 4 Recapitulation Equation
Model Parameter Relations between the QS_R+T and the Call, DWT. For
Regular Mixed sailing Patterns+Trampers
|
Equation Model |
R2 |
| |
|
Call vs QS_R+T, DWT |
Call = |
99.15 |
207.1 |
|
Call vs QS_R+T Call vs DWT |
Call = Call = |
95.98 99.14 |
384.1 216.4 |
|
DWT vs QS_R+T, Call |
DWT = |
99.58 |
-5166 |
|
DWT vs QS_R+T |
DWT = |
97.16 |
7259 |
|
DWT vs Call |
DWT = |
99.14 |
-9067 |
QS_R+T vs Call, DWT |
QS_R+T
= |
97.20 |
-8506 |
QS_R+T
vs Call |
QS_R+T
= |
95.98 |
-2879 |
QS_R+T
vs DWT |
QS_R+T
= |
97.16 |
-1212 |
For Call versus QS_R+T, the associated parameters
are known as =384.1 and
1= 0.0120. This means that an increase in
shiploads will be followed by a growth in ship visits, where if the cargo
increases by 1%, the growth in ship capacity will increase by 0.0128%.
Meanwhile, Call versus DWT parameters are known as
=216.4 and
1= 0.0229. This means that the
increase in DWT will affect the growth of ship visits, where if the DWT
increases by 1%, the growth of ship calls will increase by 0.0229%. In such
context of the Call and DWT relationship, if the DWT demand increases while the
Call for ships is still available in a certain time unit, then the addition of
DWT can be done by adding Call up to the maximum point. However, if there is no
vessel Call, then it is necessary to build a new ship to meet the growing
demand of DWT ships. Likewise, for DWT versus QS_R+T
and Call known parameters
o=-5166,
1=0.1355 and
2=32.35 it means that the growth
of QS_R+T and Call has a positive effect on DWT, and if
there is a constant ceteris paribus, then growth of 1% for QS_R+T
and Call will have an impact on changes in Call of QS_R+T=0.1355%
as well as Call=32.35%.
For DWT versus QS_R+T
with parameters of o=7259 and
1=0.5243, the increase in shiploads will be followed by
the growth of the ship's DWT, where if the cargo increases by 1%, the growth in
ship capacity will increase by 0.5243%. Meanwhile, DWT versus Call
parameters with
0=-9067 and
1=43.17 that the increase in Call will be followed by DWT
growth, where if Call increases by 1%, the DWT growth for ships will increase
by 43.17%. In the context of the DWT and Call relationship, if the call request
rises while the ship's DWT is still available in a certain time unit, then the
addition of a Call is very much determined by the DWT growth up to the maximum
point. Furthermore, if there is no growth in the ship's DWT, the ship call can
be increased to ensure the fulfillment of transportation goods at a certain
time unit.
For QS_R+T versus Call parameters with o=-8506 and
1=16.7, it describes that
the growth of QS_R+T will be negative or non-existent
if there are no ship visits in an area, whereas if Call grows by 1%, then the
change in QS_R+T will occur by 41.1%, and if the growth
of QS_R+T is positive while the number of calls remains, an increase
is required. DWT ship capacity of 2=2.24%
if the Call of the ship is considered constant ceteris paribus. Therefore, to
anticipate the growth of QS_R+T, it shall be done by increasing the
load capacity, which is usually by adding new vessels (making or renting), or
it can also be improved by increasing the call frequency of existing ships if
possible.
For
the relationship QS_R+T versus Call with the known parameters of =-2879 and
1=79.85,
the growth of QS_R+T
will be negative or non-existent if there is no call growth, whereas if
the Call occurs by 1%, the change in QS_R+T will occur by 79.85%.
For
QS versus DWT with the known parameters of =-1212 and
1=1.85, an increase in ship
loading capacity will be followed by a growth in cargo, where if the cargo
increases by 1%, the growth in ship capacity will increase by 1,85%.
Modeling of
operating ship patterns applied in islands to increase shipping efficiency is
done by Fuzzy MADM. The results of the three shipping patterns showed that the
mixed regular and tramper shipping patterns could improve ship sailing
performance with a value of 13.00 higher than the regular value of 9.80 and the
tramper of 10.60. And by using the transportation performance data ( QS_R+T,
Call, DWT) in Table 3, it is known that the availability of QS_R+T
cargoes greatly affects the demand for Call and DWT vessels. The addition of Call and DWT will have
a positive impact on the growth of QS_R+T to support the Maluku Sea
Highway. The implications of this model can be used to measure the growth of
transportation performance in islands by determining shipping patterns and
dimensions of transportation infrastructure that are universally applicable and
can be used in areas that have the same characteristics, especially in the
Eastern regions of Indonesia.
This study aims to determine
the optimal shipping pattern in the Maluku region to support the sea
Highway program in Indonesia. The
results indicate that the best ship operating pattern, determined using the
Fuzzy MADM method, is a combination of regular and tramper sailing, known as a mixed
sailing pattern. Increasing the productivity of QS_R+T and DWT ships will have
a positive effect on ship visits in a certain time unit. If the potential
growth in positive cargo QS_R+T > Call and DWT, then it is
necessary to build new ships with optimal DWT to increase ship efficiency in
supporting the Sea Highway program. Thus the increase in Call
and DWT for ships requires adjustment to cargo availability in the archipelago. The implications of this research can be used as a reference for consideration for policies making on the development of sailing patterns in the archipelago,
as well as being able to improve the economy of the archipelagic community through optimal shipping access
as an effort to build regional economic strength to overcome economic
disparities between archipelagic regions. Suggestion: The need for
further studies between the government as policymakers and academics to see how
far the impact of sailing has on increasing LF in small island areas where
Call, DWT and Qs are variables that influence economic development.
The authors would like to thank the Ministry of Transportation of the
Republic of Indonesia for researching the Port Master Plan in Maluku 2016,
Pattimura University for providing PNDP Research funding No. 926/UN13/SK/2022
and all parties who have contributed to this research so that this paper can be
completed properly.
Amelia, P., Lathifah,
A., Yasa, I.N.A, 2021. Analysis of the Impact of Maritime Sector
Development in Supporting Indonesian Navy Ship Operations. Procedia Computer
Science, Volume 197, pp. 317–325
Banerjee, A., Duflo, E., Qian, N., 2020. On The Road:
Access to Transportation Infrastructure and Economic Growth in China. Journal of
Development Economics, Volume 145, Volume 2020, p. 102442
Esmail, H.A.H., 2016. Efficiency Assessment of
Jazan Port Based on Data Envelopment Analysis. Mediterranean
Journal of Social Sciences, Volume 7, p. 320
Goodarzi, F., Abdollahzadeh, V., Zeinalnezhad,
M., 2022. An Integrated Multi-Criteria Decision-Making
and Multi-Objective Optimization Framework for Green Supplier Evaluation and
Optimal Order Allocation Under Uncertainty. Decision Analytics Journal, Volume 4, p.
100087
Hozairi, Lumaksono, H., Tukan, M.,
Buhari, 2019. Assessment of the Most Influential Factors on Indonesian Maritime Security
Using Fuzzy Analytical Hierarchy Process. In: Proceedings - 2019
International Conference on Computer Science, Information Technology, and
Electrical Engineering ICOMITEE, pp. 74–81
Jaal, Z., Abdullah, J., 2012. User’s
Preferences of Highway Landscapes in Malaysia: A Review and Analysis of the
Literature. Procedia - Social and Behavioral Sciences, Volume 36, pp. 265–272
Kozonogova, E., Dubrovskaya, J., Dubolazova, Y., 2020.
Assessment of the Contribution of Inter-Territorial Interaction in the
Development of the National Economy. International Journal of Technology,
Volume 11(6), pp. 1161–1170
Kumar, A., Maheshwari, S., Sharma,
S.K., 2015. Fuzzy Logic Optimization of Weld Properties for SAW Using Silica Based
Agglomerated Flux. Procedia Computer Science, Volume 57, pp. 1140–1148
Lumaksono, H., 2018. The selection of suitable fishing gear
for fishermen in Madura Island using Fuzzy AHP and Fuzzy TOPSIS. Ecoterra,
Volume 15(2), pp. 34–51
Nurkholis, Nuryadin, D., Syaifudin, N., Handika, R.,
Setyobudi, R.H., Udjianto, D.W., 2016. The Economic of Marine Sector in
Indonesia. Aquatic Procedia, Volume 7, pp. 181–186
Santos, T.S., Portugal, L.d.S., Ribeiro, P.C.M., 2021.
Evaluating The Performance Of Highway Concessions Through Public-Private
Partnerships Using A Fuzzy Multi-Criteria Decision-Making Procedure. Transportation
Research Interdisciplinary Perspectives, Volume 10, p. 100399
Tukan, M., 2021. Optimalisasi Dimensi Transportasi Laut
Berbasis Potensi Ekonomi Wilayah Pulau (Optimizing Sea Transportation
Dimensions Based on the Economic Potential of Island Regions). In:
Seminar Nasional Archipelago Engineering 2021
Tukan, M., Achmadi, T., Widjaja, S., 2015. Seaport
Dimensional Analysis towards Economic Growth in Archipelagic Regions.
International Journal of Technology, Volume 6(3), pp. 422–431
Tukan, M., Achmadi, T., Wijaya, S., Ciptomulyono, U., 2012.
Modelling Ports Investment and Island Economic Growth. IPTEK The Journal for
Technology and Science, Volume 23(3),
pp. 120–126
Tukan, M., Camerling, B.J., Afifudin, M.T., Hozairi, 2020.
Decision Support System for Determining Floating Dock Locations in Maluku
Islands Using AHP-TOPSIS. Journal of Physics: Conference Series, Volume 1577(1),
p. 012001
Wang, C., Wang, J., 2011. Spatial Pattern of The
Global Shipping Network and its Hub and-Spoke System. Research in Transportation Economics, Volume 32(1), pp.
54–63
Xu, F., Gao, K., Xiao, B., Liu, J., Wu, Z., 2022. Risk
Assessment for The Integrated Energy System Using a Hesitant Fuzzy
Multi-Criteria Decision-Making Framework. Energy Reports, Volume 8, pp. 7892–7907
Zhogova, E., Zaborovskaia, O., Nadezhina,
O., 2020. An analysis of the Indicators of Regional Economy Spatial Development
in the Leningrad Region of Russia. International Journal of Technology, Volume 11(8), pp. 1509–1518
