COVID-19 Spread Modeling Considering Vaccination and Re-Morbidity
Corresponding email: gintsyak_am@spbstu.ru
Published at : 27 Dec 2022
Volume : IJtech
Vol 13, No 7 (2022)
DOI : https://doi.org/10.14716/ijtech.v13i7.6186
Borovkov, A.I., Bolsunovskaya, M.V., Gintciak, A.M., Rakova, V.V., Efremova, M.O., Akbarov, R.B., 2022. COVID-19 Spread Modeling Considering Vaccination and Re-Morbidity. International Journal of Technology. Volume 13(7), pp. 1463-1472
| Aleksey I. Borovkov | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
| Marina V. Bolsunovskaya | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
| Aleksei M. Gintciak | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
| Valeriya V. Rakova | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
| Marina O. Efremova | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
| Ruslan B. Akbarov | Peter the Great St. Petersburg Polytechnic University, 29 Polytechnicheskaya st., St. Petersburg, 195251, Russian Federation |
To effectively counter
the COVID-19 spread, using scientifically based decision-making methods in this
area is required. The disease characteristics and the methods applied to stem
it are constantly changing, so it is necessary to update existing methods for
predicting the COVID-19 spread in light of new trends. The present paper deals
with developing a new SVEIRS model from the SEIR class, taking into account the
vaccination campaign and the possibility of recurrent morbidity cases. These
improvements make it possible to increase the accuracy of the disease spread
prediction due to a more direct correspondence to reality. The developed SVEIRS
model was verified when predicting the COVID-19 spread in Moscow in
July-September of 2022 and showed higher prediction accuracy compared to the
SEVIS reference model. Based on the developed model, it is possible to predict
the COVID-19 spread in various regions to form an optimal vaccination campaign
strategy.
COVID-19; Epidemiology; Infection spread; Simulation modeling; System dynamics
At the end of 2019, the pandemic of the new
coronavirus infection SARS-CoV-2 swept the world. The COVID-19 pandemic became
geographically widespread; the virus rapidly affected the world's population in
every corner of the globe (Rothan & Byrareddy,
2020). For more than two years, humanity has been countering this
disease. Several waves of increase and decrease in COVID-19 spread were
observed.
Regarding the frequent cases of the
population's recurrent morbidity, vaccination and revaccination remain the most
effective measures to counter infection (Pilz et
al., 2021). Due to these measures, the virus's contagiousness is reduced
and the number of death cases among the vulnerable proportion of the
population. From the economic perspective, vaccination is the most effective
measure to stem coronavirus infection, since the vaccinated part of the
population has the right to return to their usual lifestyle, earn and consume,
which causes the country's economy to grow (Berawi,
2021). To fully restore the global economy and prevent the emergence of
new variants of coronavirus infection, it is required to vaccinate at least 70%
of the world population. Thus, the development of a proper vaccination
strategy, taking into account the regional, individual characteristics of
various population groups, is a complex and time-consuming process,
implementing such a strategy makes it possible to form collective
immunity, reduce the economic burden (Polyanin et
al., 2020), increase the vaccination attractiveness.
Traditional approaches to modeling the
infectious disease spread have a significant disadvantage in the form of
"uncertainty" parameters that are difficult to measure. These are
indicators of mobility and population homogeneity, which also assumes a
proportional infection spread among the entire population. It is generally
incorrect. In the early stages of the pandemic, the incubation period, the
infectivity period, the patient isolation period, the time and effectiveness of
immunity after the disease, and later the effect of vaccination was considered
as uncertain indicators. In this connection, such predictions were approximate,
short-term, requiring a scenario approach (Klyushin,
2022). Models do not only predict events but also describe possible
outcomes and scenarios for the pandemic development. The use of simulation
modeling, machine learning, and interpolation methods make it possible to solve
this problem due to the principle of trainability on samples and data obtained
as a result of experiments. Moreover, it is worth noting that with the course
of the COVID-19 infection, several additional factors affecting the modeling
results accuracy have appeared, in particular, the population recurrent
morbidity, revaccination which requires current models calibration.
The above determines the relevance of the
current study and the urgent need to develop a simulation model considering the
above factors and generating highly accurate realistic predictions on
coronavirus infection spread based on the methodology of mathematical modeling
and dynamic prediction of the COVID-19 spread.
This research aims to develop a new
SVEIRS (“Susceptible – Vaccinated – Exposed – Infected – Recovered –
Susceptible”) model from the SEIR (“Susceptible – Exposed – Infected –
Recovered”) class (Li et al., 2021), taking
into account the vaccination campaign and the possibility of recurrent
morbidity cases. Within the present study, simulation modeling tools were
considered from the perspective of applicability for predicting the infectious
diseases spread, taking into account recurrent morbidity and vaccination.
2.1. Infectious
disease spread modeling
Simulation modeling is a quantitative method of making and supporting
decisions. A digital model of the system under study is created to evaluate and
predict its effectiveness in real-world conditions. System analysis is used as
the methodological basis for simulation modeling, classifying it as system
modeling. The method's main feature is the possibility of reproducing the
system under study without losing the dynamics of the system element's
interaction. The research method is based on simulation and an experimental
approach, which enables distinguishing it from mathematical modeling based on a
computational approach.
Mathematical modeling provides possibilities for studying systems that
change under the influence of random factors. At the same time, simulation
models are widely used in the study of stochastic and deterministic systems and
are applicable to solving complex problems under uncertainty (Lychkina,
2005). For managers and health services, simulation
modeling is of key importance when making decisions since it allows studying
and evaluating the effect of various alternative solutions, situations and
conditions (Borovkov et al., 2020).
The modeling method selection should be based on the requirements,
problems, and complexity of the system under study. Currently, the following
methods of simulation modeling are widely used (Currie et al., 2020).
System dynamics based on creating simultaneous differential equations that
reflect resources (human, material), the connections between them, and the
importance (criticality) of these connections for the system. The most
essential elements of system dynamics are the feedback loops and delays, which
make it possible to explain the system's behavior. The SIR
(suspected-infected-recovered) model is the most widely used in predicting the
spread of infectious diseases. The SIR model and models based on it are
designed to support strategic decisions that have consequences for the entire
population of a country or region (Branding, 2022).
Agent-based modeling (agent-based approach) simulates the interaction
of individuals in society and allows for determining how small changes in their
behavior can affect the entire population in the area under study. Modeling
social ties and population mobility becomes critically important in the need’s
context to ensure high accuracy in predicting the spread of infectious disease (Makarov et al., 2020). Agent
models are stochastic because they assume and consider many human behavior
scenarios. Due to this, the models can predict the effectiveness of management
decision-making, even under the impermanence (changeability) of the
population’s behavior.
Discrete-event approach (simulation) involves using stochastic
models that consider the spread (delay and variability) of time between the
measures taken by the authorities and the onset of their impact on the system
(epidemiological situation). The discrete-event approach is widely used to simulate
the operation of systems in time, in which such system elements as people,
agents, tasks, and messages (information) undergo the procedures of queues and
operations. A typical application area of such models is the assessment of the
medical resources (e.g., doctors and nurses) availability impact for the
waiting time and the number of items in the queue (for example, patients).
Having studied the existing paradigms of simulation modeling, a group of
authors of the present research concluded that the system dynamics methods
application is the most appropriate, particularly SIR class models. They are
possible to take into account a large number of factors without significantly
reducing the modeling accuracy. This approach is applicable under incomplete
information and uncertainty. Moreover, it gives the opportunity of dynamically
changing environment and the possibility of simulating numerous scenarios. The
key argument for the system dynamics selection was the possibility of taking
into account a large number of causality chains and identifying functional
dependencies between various factors, which makes it possible to accurately
simulate the system's behavior (Yusoff &
Izhan, 2020).
The analysis of existing methods of modeling and predicting the spread of
infectious diseases and the distinctive features of the coronavirus infection
progress allowed us to determine a mechanistic Kermack-McKendrick SEIR model as
a basis for the experimental model development. It appears to be the most valid
model that provides sufficient prediction accuracy in the medium term.
The current study proposes an extension of the SEIR model to the SVEIRS
model by adding appropriate elements and interconnections between them. The
model considers a significant number of factors affecting the dynamics of the
COVID-19 spread for the complete simulation of a real system.
2.2. Model description
The SVEIRS model developed within the current study is based on the system
dynamics principles and are simultaneous differential equations linking
reserves (categories of the population to the COVID-19 morbidity process) via
flows (infection, vaccination, and recovery processes) and converters (the
morbidity process parameters).
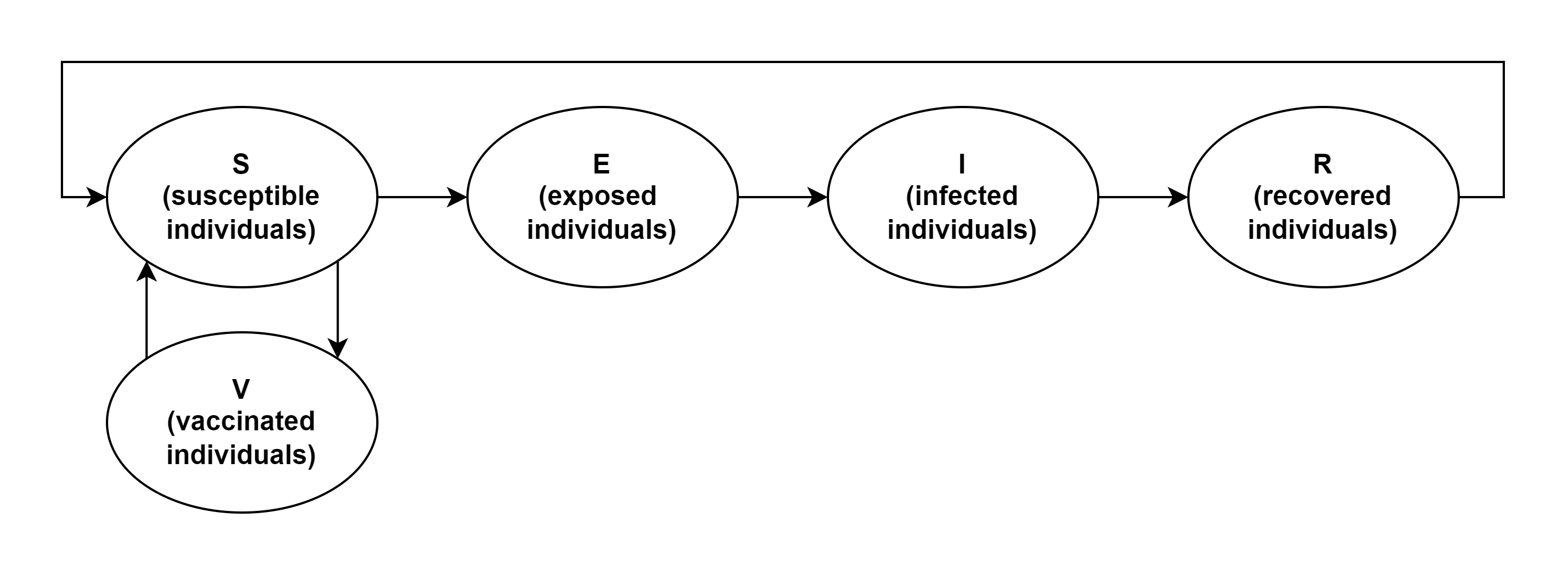
In addition to the basic population categories for SEIR class models (S -
Susceptible, E - Exposed, I - Infected, R - Recovered), the SVEIRS model
includes an additional type: V - Vaccinated.
The developed SVEIRS model is described by the following simultaneous differential equations (1)–(5):
where S(t) is the number of susceptible individuals at time t; V(t) is the number of vaccinated individuals with artificial immunity (acquired via vaccination) at time t; E(t) is the number of exposed individuals at time t; I(t) is the number of infected individuals at time t; R(t) is the number of recovered individuals with natural immunity (acquired as a result of a previous disease) at time t; v(t) is the absolute rate of vaccination campaign, people per day; ? - the relative frequency of effective (leading to disease transmission) contacts of individuals - the value is determined during calibration; ?- the relative frequency of individual’s transition from the Recovered (R) category to the Susceptible (S) category - the value inversely proportional to the natural immunity duration; ?- the relative frequency of individual’s transition from the Vaccinated (V) category to the Susceptible (S) category - the value inversely proportional to the artificial immunity duration; ? - the relative frequency of individual’s transition from the Exposed (E) category to the Infected (I) category - the value inversely proportional to the incubation period duration; ?- the relative frequency of individual’s transition from the Infected (I) category to the Recovered (R) category - the value inversely proportional to the disease duration.
Figure 1 shows the block diagram of the developed SVEIRS model.
Figure
1 Block diagram of the developed SVEIRS model
In addition to the dependencies widely used in SEIR
class models, there are two critical features in the developed SVEIRS model.
Firstly, the model considers the vaccination campaign
as a way to reduce morbidity by minimizing the number of susceptible
individuals at risk. Vaccinated individuals are identified as a separate
category linked by flows only to the category of susceptible individuals. The
absolute rate of vaccination campaign determines the rate of this category of
individuals replenishment, depends on government measures to vaccinate the
population and the propensity of the people to vaccinate, therefore, within the
model, it is an external parameter. The rate of this category of individuals
withdrawals is determined by the rate of termination of artificial immunity
acquired via vaccination. The relative rate of individuals transitioning into
the category of susceptible is inversely proportional to the duration of the
artificial immunity effect obtained via vaccination.
Secondly, the model considers the possibility of
recurrent morbidity as an additional source of susceptible individuals. Unlike
traditional SEIR models, in this case, recovered individuals are susceptible to
the recurrence of the same disease not forever, but for a certain period equal
to the duration of the natural immunity acquired due to the previous disease.
Considering the recurrent COVID-19 cases, this model extension makes it more
realistic. The recurrent morbidity possibility is implemented as a result of
combining an additional flow between the Recovered (R) and Susceptible (S)
categories, the rate of individuals transition which is determined by the rate
of termination of the natural immunity acquired as a result of the previous
disease. The relative rate of individuals growth into the category of
susceptible is inversely proportional to the duration of the natural immunity
acquired due to the previous disease.
The main reference model for the developed SVEIRS model is the SEVIS (“Susceptible – Exposed – Vaccinated – Infected – Susceptible”) model (Li et al., 2021), which is described by the following simultaneous differential equations:
where - the proportion of the disease cases ending with
the immunity acquisition. The
other symbols were described in formulas (1)–(5).
Figure 2 shows the block diagram of the SEVIS reference model.
Figure 2
Block diagram of the SEVIS reference model
The SEVIS reference model is also an extension of the
SEIR model. It was created by adding a vaccination campaign and the recurrent
morbidity possibility to the model. However, this extension is implemented
differently than in the developed SVEIRS model. The vaccination process is
one-sided, i.e., once vaccinated against COVID-19, an individual receives
permanent immunity to the disease. At the same time, individuals fall into the
Vaccinated (V) category not only after vaccination but also with some probability
after the disease. Thus, the Vaccinated (V) category in the SEVIS model
contains individuals with the artificial and natural immunity. In addition, both types of immunity are
indefinite, which is contrary to the actual dynamics of the disease spread.
Table
1 compares the SEVIS and SVEIRS models regarding vaccination features and the
possibility of recurrent morbidity.
Table 1 Comparison of
SEVIS and SVEIRS models
|
|
SEVIS reference model (Li et al., 2021) |
Developed SVEIRS model |
|
Vaccination
campaign |
A separate category of
Vaccinated (V) individuals. A flow from the Susceptible (S) category,
depending on the relative rate of the vaccination campaign. No reverse flow
is provided. |
A separate category of
Vaccinated (V) individuals. A flow from the Susceptible (S) category,
depending on the total rate of the vaccination campaign. The reverse flow
into the Susceptible (S) category, depending on the duration of the immunity
acquired via vaccination. |
|
Recurrent
morbidity |
Some individuals
are transferred to the Susceptible (S) category after the disease. Another
part of individuals after the disease is assigned to the Vaccinated (V)
category. |
All individuals after the disease are moved to the
Recovered (R) category and receive natural immunity. The flow from the
Recovered (R) category to the Susceptible (S) variety depends on the duration
of the immunity acquired due to the previous disease. |
Even though both models are SEIR class model
extensions and additionally consider the same set of disease features and ways
to stem its spread, these features are implemented in different ways in the
models, which affects the simulation experiments with these models.
Within
the present research, both models are verified on the same data set to assess
their functional features. Moscow is chosen as the modeling object. For the
model calibration historical data on the number of infected (I, Infected
individuals) in Moscow from 07/01/2022 to 07/30/2022 (30 days) will be used.
The prediction accuracy estimation will be carried out on the relevant data
from 07/31/2022 to 09/28/2022 (60 days), which corresponds to the medium-term
prediction horizon.
The
parameters of the models are deduced from historical data on the COVID-19
incidence in Moscow and modern publications studying the COVID-19 features
(Table 2).
For the selection the relative frequency of effective contacts the calibration of models based on historical data on the number of infected (I, Infected individuals) in Moscow from 07/01/2022 to 07/30/2022 (30 days) has been performed. Figure 3 shows the data series of the SVEIRS and SEVIS models at the calibration time interval to the actual data at the same time interval.
Table 2 Model parameters
|
Parameter |
Value in the SEVIS reference model |
Value in the developed SVEIRS model |
|
The
initial number of susceptible individuals, S(0), people (Stopkoronavirus.rf,
2022) |
10,958,609 |
|
|
The initial
number of vaccinated individuals, V(0), people (Stopkoronavirus.rf, 2022) |
1,500,649 |
782,616 |
|
The initial
number of exposed individuals, E(0), people (Stopkoronavirus.rf, 2022) |
29,368 |
|
|
The initial
number of infected individuals, I(0), people (Stopkoronavirus.rf, 2022) |
146,840 |
|
|
The initial
number of infected individuals, R(0), people (Stopkoronavirus.rf, 2022) |
- |
718,033 |
|
Relative
frequency of effective contacts, 1 / (people * day) |
it is determined during the calibration process |
|
|
The absolute rate
of vaccination campaign, v, people per day (Stopkoronavirus.rf, 2022) |
- |
386 |
|
Relative rate of
the vaccination campaign, 1 / day (Stopkoronavirus.rf,
2022) |
1 / 28,390 |
- |
|
Relative
frequency of individual’s transition from the Recovered (R) category to the
Susceptible (S) category, 1 / day (Dan
et al., 2021) |
- |
1 / 180 |
|
Relative
frequency of individual’s transition from the Vaccinated (V) category to the
Susceptible (S) category, 1 / day (Lopez
Ledesma et al., 2021) |
- |
1 / 180 |
|
Relative frequency of individual’s
transition from the Exposed (E) category to the Infected (I) category, 1 /
day (Hay et al., 2022) |
1 / 2 |
|
|
The relative frequency of an
individual’s transition from the Infected (I) category to other categories, 1
/ day (Hay et al., 2022) |
1 / 10 |
|
|
The proportion of the disease cases
ending with immunity acquisition. (Li et al., 2021) |
0.8 |
- |
Figure 3 Data series of the
SVEIRS and SEVIS models with real data in the interval from 07/01/2022 to
07/30/2022
Table 3 demonstrates
calibration results. As part of the calibration, a value of the relative
frequency of effective contacts has been selected for both models. The same
parameter value has been chosen for both models as a result of the calibration.
The chosen value minimizes the mean percentage absolute error (MAPE) to the
nearest thousandths. Table 3 also provides the value of the square root of the
root-mean-square error for the calibration accuracy (and further prediction)
interpretability.
Table 3 Models calibration
results in the interval from 07/01/2022 o 07/30/2022
|
|
SEVIS reference model |
Developed SVEIRS model |
|
Relative frequency of effective contacts, 1 / (people * day) |
0.064 | |
|
MAPE |
0.300% |
0.299% |
|
RMSE, people |
573.340 |
571.647 |
The calibration accuracy of the SEVIS and SVEIRS
models using data series from 07/01/2022 to 07/30/2022 is comparable. It makes
possible to evaluate the accuracy of prediction models using data series in the
interval from 07/30/2022 to 09/28/2022 compared to actual data (Figure 4).
Figure 4 Prediction data series of the SVEIRS and SEVIS models
with real data in the interval from 07/31/2022 to 09/28/2022
Table
4 shows indicators of the prediction accuracy of the COVID-19 spread in Moscow
from 07/31/2022 to 09/28/2022 using SEVIS and SVEIRS models.
Table 4 Indicators of the SEVIS and SVEIRS models prediction accuracy
|
|
SEVIS reference model |
Developed SVEIRS model |
|
MAPE |
6.309% |
3.329% |
|
RMSE, people |
14,374.837 |
7,772.028 |
The
results of the COVID-19 spread modeling using SEVIS and SVEIRS models allow us
to claim a higher prediction accuracy of the developed SVEIRS model in this
case.
4. Discussion
For a more reliable SEVIS and SVEIRS models accuracy
assessment, it is required to simulate the COVID-19 spread on data corresponding
to other regions and time intervals. Within the present paper, the application
of the SEVIS reference model and the developed SVEIRS model to modeling the
COVID-19 spread in one region (Moscow) in the interval of 90 days (30 days for
calibration and 60 days for evaluation) has been considered.
Prediction accuracy
depends not only on the model and the features of the modeling object, but also
on the prediction horizon. Thus, particular models may have high accuracy in
short term prediction, but may be inappropriate for long-term prediction, and
vice versa. Although the developed SVEIRS model has shown higher prediction
accuracy in the considered case, during its development, assumptions were made,
the elimination of which can bring the model behavior closer to the conduct of
the real system.
Firstly, in the
SVEIRS model, only one disease variant is constantly active. In contrast, the
SARS-CoV-2 virus that causes COVID-19 has several thousand variants (Koyama et al., 2020), some of which cause mutually
independent morbidity waves. It shows that the natural immunity obtained from
one virus variant disease does not always prevent infection with another virus
variant (Tang et al., 2020). In addition,
vaccines' effect is often directed at particular virus variants (Callaway, 2021).
Secondly, in the SVEIRS model, it is assumed that vaccination is available only to susceptible individuals, and the possibility of vaccination of individuals with natural or artificial immunity is not considered, although such cases are undoubtedly encountered in real life. However, this assumption is inherent in most SEIR class models that consider the vaccination campaign (Johnston et al., 2022).
Thirdly, the SVEIRS model assumes that all recovered individuals acquire natural immunity, and all vaccinated individuals acquire artificial immunity. At the same time, there are cases of individuals recurrent morbidity shortly after the disease. In addition, none of the existing COVID-19 vaccines has absolute efficacy (Huang et al., 2022). The correction for the probability of acquiring natural immunity and the effectiveness of vaccines can be made in the SVEIRS model extensions.
The paper describes the developed SVEIRS model, the SEIR class model
extension created by considering the vaccination campaign and the possibility
of recurrent morbidity. The developed model makes it possible to predict the
spread of infectious diseases (including COVID-19) characterized by the
prospect of acquiring natural immunity due to the previous disease and
artificial immunity via vaccination. The developed SVEIRS model was verified
when predicting the COVID-19 spread in Moscow in July-September of 2022
compared to the SEVIS reference model. SVEIRS model showed higher prediction
accuracy. Based on the developed model, it is possible to predict the COVID-19
spread in various regions to form an optimal vaccination campaign strategy.
The
research is funded by the Ministry of Science and Higher Education of the
Russian Federation as part of the World-class Research Center program: Advanced
Digital Technologies (contract No. 075-15-2022-311 dated 20 April 2022).
Berawi M.A., 2021. Innovative Technology for
Post-Pandemic Economic Recovery. International Journal of Technology,
Volume 12(1), pp. 1–4
Borovkov, A.I., Bolsunovskaya, M.V., Gintciak,
A.M., Kudryavtseva, T.Yu., 2020. Simulation Modelling Application for
Balancing Epidemic and Economic Crisis in The Region. International Journal
of Technology, Volume 11(8), pp. 1579–1588
Branding, N., 2022. Prediction of The
Number of Weekly Covid-19 Infections: A Comparison of Machine Learning Methods.
Master Degree Project in Informatics with a Specialization in Data Science. Available online at
https://www.diva-portal.org/smash/get/diva2:1672236/FULLTEXT01.pdf, Accessed on September 30, 2022
Callaway, E., 2021. Mix-and-match COVID Vaccines
Ace The Effectiveness Test. Nature, Volume 21
Currie, C., Fowler, J.W., Kotiadis, K., Monks, T., Onggo,
B.S., Robertson, D.A. and Tako, A.A., 2020. How Simulation
Modelling Can Help Reduce The Impact of COVID-19. Journal of Simulation,
Volume 14(2), pp. 83–97
Dan, J. M., Mateus, J., Kato, Y., Hastie, K.M., Yu, E.D.,
Faliti, C.E., Grifoni, A., Ramirez, S.I., Haupt, S., Frazier, A., Nakao, C.,
2021. Immunological Memory to SARS-Cov-2 Assessed for Up to 8 Months After
Infection. Science, Volume 371(6529), p. eabf4063
Hay, J.A., Kissler, S.M., Fauver, J.R., Mack, C., Tai, C.G.,
Samant, R.M., Connolly, S., Anderson, D.J., Khullar, G., MacKay, M., Patel, M.,
2022. Quantifying The Impact of Immune History and Variant On SARS-Cov-2 Viral
Kinetics and Infection Rebound: A Retrospective Cohort Study. Elife, Volume
11, p.e81849
Huang, Z., Su, Y., Zhang, T., Xia, N., 2022.
A Review of The Safety and Efficacy of Current COVID-19 Vaccines. Frontiers
of Medicine, Volume 16(1), pp. 39–55
Johnston, M., Pell, B., Nelson, P., 2022. A
Mathematical Study of COVID-19 Spread by Vaccination Status in Virginia. Applied
Sciences, Volume 12
(3), p. 1723
Klyushin, D., 2022. Comparing Predictive Accuracy of COVID-19
Prediction Models: A Case Study. Decision Sciences for COVID-19, Volume
320, pp. 165–179
Koyama, T., Platt, D., Parida, L., 2020.
Variant Analysis of SARS-Cov-2 Genomes. Bulletin of the World Health
Organization, Volume 98(7), pp. 495–504
Li, Y., Ge, L., Zhou, Y., Cao, X., Zheng, J., 2021. Toward the
Impact of Non-pharmaceutical Interventions and Vaccination on the COVID-19
Pandemic with Time-Dependent SEIR Model. Frontiers in Artificial
Intelligence, Volume 4, p. 648579
Lopez Ledesma, M.M.G., Sanchez, L., Ojeda,
D.S., Rouco, S.O., Rossi, A.H., Varese, A., 2021. Temporal Increase in
Neutralization Potency of SARS-CoV-2 Antibodies and Reduced Viral Variant
Escape after Sputnik V Vaccination. medRxiv.
Lychkina, N., 2005. Imitacionnoe Modelirovanie
Ekonomicheskih Processov (Modeling of Economic Processes). M.: Finansy i statistika (Finance
and statistics), Volume 164
Makarov, V.L., Bakhtizin, A.R., Sushko, E.D., Ageyeva, A.F.,
2020. Modelirovanie Epidemii COVID-19-Preimushchestva Agent-Orientirovannogo
Podhoda (COVID-19 Epidemic Modeling-Advantages of An Agent-Based Approach).
Economic and social changes: facts, trends, forecast, Volume
13(4), pp. 58–73
Pilz, S., Chakeri, A., Ioannidis, J.P., Richter, L., Theiler-Schwetz,
V., Trummer, C., Krause, R., Allerberger, F., 2021. SARS-CoV-2 Re-infection Risk
in Austria. European journal of clinical investigation, Volume 51(4), p.
e13520
Polyanin A., Pronyaeva L., Pavlova A.,
Fedotenkova O., Rodionov D. 2020. Integrated Approach for Assessing the
Economic Security of a Cluster. International Journal of Technology,
Volume 11(6), pp. 1148–1160
Rothan, H.A., Byrareddy, S.N., 2020. The Epidemiology and
Pathogenesis of Coronavirus Disease (COVID-19) Outbreak. Journal of
Autoimmunity, Volume 109, p. 102433
Stopkoronavirus.rf, 2022. The Official Internet
Resource for Informing The Public About Coronavirus (COVID-19). Available online at https://stopcoronavirus.rf, Accessed on September 30,
2022
Tang, X., Wu, C., Li, X., Song, Y., Yao, X., Wu, X.,
Duan, Y., Zhang, H., Wang, Y., Qian, Z., Cui, J. 2020. On The Origin
and Continuing Evolution of SARS-CoV-2. National Science Review, 7(6),
pp. 1012–1023
Yusoff, M., Izhan, M., 2020. The Use of System
Dynamics Methodology in Building a COVID-19 Confirmed Case Model. Computational and
Mathematical Methods in Medicine, Volume 11
