A Novel Design and Performance Analysis of Piezoelectric Energy Harvester with Application to a Vehicle Suspension System Moving on Uniform Bridges
Corresponding email: edwa005@brin.go.id
Published at : 10 Jul 2024
Volume : IJtech
Vol 15, No 4 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i4.6155
Hikmawan, M.F., Azhari, B., Yazid, E., Nugraha, A.S., Mirdanies, M., 2024. A Novel Design and Performance Analysis of Piezoelectric Energy Harvester with Application to a Vehicle Suspension System Moving on Uniform Bridges. International Journal of Technology. Volume 15(4), pp. 1133-1147
| Muhammad Fathul Hikmawan | Research Center for Smart Mechatronics, National Research and Innovation Agency (BRIN), Bandung, 41035, West Java, Indonesia |
| Budi Azhari | Research Center for Smart Mechatronics, National Research and Innovation Agency (BRIN), Bandung, 41035, West Java, Indonesia |
| Edwar Yazid | Research Center for Smart Mechatronics, National Research and Innovation Agency (BRIN), Bandung, 41035, West Java, Indonesia |
| Aditya Sukma Nugraha | Research Center for Smart Mechatronics, National Research and Innovation Agency (BRIN), Bandung, 41035, West Java, Indonesia |
| Midriem Mirdanies | Research Center for Smart Mechatronics, National Research and Innovation Agency (BRIN), Bandung, 41035, West Java, Indonesia |
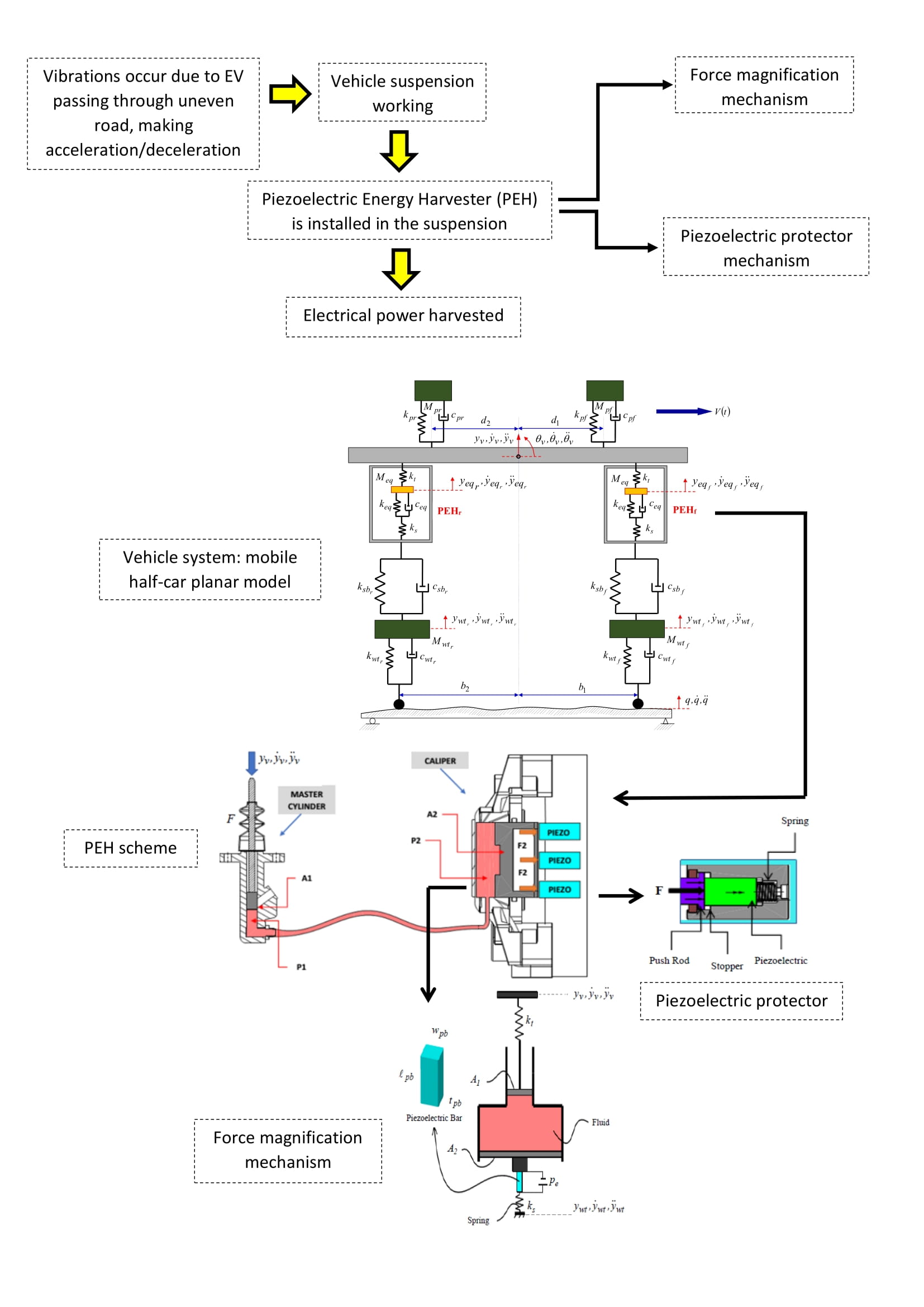
The development
of energy recovery systems in vehicles is a form of synergy between energy efficiency
and renewable energy to overcome the energy crisis and global warming problems.
This paper addresses such challenges by introducing a novel design of a
piezoelectric energy harvester (PEH) for a vehicle
suspension system. The PEH is designed to capture the linear vibration of the
suspension system subjected to road surface roughness and move on uniform bridges. The vibration is
amplified by a pressurized liquid cylinder-piston mechanism which deforms the
piezoelectric bar to produce electric power. An additional novel mechanism in the form of a
piezoelectric protector is also proposed to avoid physical damage due to
excessive unidirectional compressive force as a result of an unpredictable
uneven road. Given the key design parameters, the
electric power can be harvested up to 67.5 W for a PEH with a span of 150 m of
the bridge, a velocity of 40 m/s, and a vehicle mass of 2,691.6 kg.
Energy harvesting; Hydraulic mechanism; Piezoelectric; Vehicle suspension
In
vehicle suspension systems, the vibrations produced due to the road surface
irregularities, acceleration, and deceleration are considered as energy losses.
Researchers have processed and reused it as a new energy source for an energy efficiency and recovery
system (e.g., a tuned vehicle damper (Alhumaid, Hess, and Guldiken, 2022; Xie et al., 2020; Pan et al.,
2017) and piezoelectric energy
harvester (PEH) (Elgamal, Elgamal, and Kouritem, 2024; Akbar et al., 2022; Azangbebil et al., 2019; Taghavifar and Rakheja, 2019; Zhao et al., 2019a; Chen et
al., 2016; Hendrowati, Guntur, and Sutantra, 2012; Jeon et al., 2005)). With the piezoelectric
transducer, an energy harvester with a specific application to a vehicle
suspension system has attracted significant attention (Du
et al., 2023; Ghormare, 2022; Sheng et al., 2022; Li et al., 2021; Darabseh et al., 2020; Morangueira and Pereira, 2020; Tavares and Ruderman, 2020; Wang et al., 2020; Lafarge et al., 2019; Shin et al., 2019; Kulkarni et
al., 2018; Tao et al., 2017; Wei and Taghavifar, 2017; Zhao et al., 2019b). However, the generated electrical power is still in the mW order. Nowadays, there is an urgent
need to enhance the electric power capacity of a PEH. To date, the existing
literatures are very limited. A new class of PEH has been proposed, such as: a
dual-mass piezoelectric
This paper enhances the aforementioned research works with the following contributions: (i) a novel design of PEH for a vehicle suspension system is presented, utilizing a pressurized liquid cylinder-piston mechanism to deform the piezoelectric material and generate electricity, (ii) a novel additional mechanism of a piezoelectric protector is proposed to avoid damage due to excessive unidirectional compressive force as a result of an unpredictable uneven road, (iii) the dynamic model of the PEH mounted on a vehicle is improved by transitioning from a mobile quarter-car model to a mobile half-car planar model that considers both the passenger and driver and moves on uniform bridges for more realistic performance (iv) performance of the proposed PEH for energy harvesting using a piezoelectric bar from PZT material is evaluated using intensive numerical simulations, and parametric study [is performed as well to support the results. The paper is organized as follows. Section 2 presents the design concept and system modeling. Section 3 provides results and discussion. Finally, conclusions are in Section 4.
Design Concept and System Modelling
The PEH is proposed to be
universally used on a wide range of vehicle suspension types. However, the
space available on the suspension section is limited. Also, the vibration level
experienced by the suspension is different for every vehicle. It leads to
variations of load exerted on the piezoelectric transducer. To harvest the
vibration energy optimally, an effective mechanism of the PEH is designed to
address those challenges.
2.1. Design Concept
Figure 1a shows the proposed PEH design concept
(Figure 1b) mounted on a vehicle suspension system. There are two main
developed mechanisms: force magnification and piezoelectric protector mechanism
(Figure 1c). The former is designed to amplify the excitation force through a
linear-spring mounted on the suspension system. It works based on a pressurized
liquid cylinder-piston mechanism known as a hydraulic system, consisting of the
master cylinder and caliper cylinder components. Due to the vehicle
suspension’s limited space, the PEH that can be mounted onto the suspension
system is limited in volume. Thus, the master cylinder components with small
volumes and easily attached must be chosen.
However, some factors such
as road surface roughness, traffic conditions, and vehicle speed dynamics may
significantly affect excitation force. If the road surface is flat with
congested traffic conditions, the vehicle suspension's excitation force may be
weak. Thus, the force magnification mechanism must be set to effectively
capture the suspension’s vibration while amplifying its magnitude
simultaneously. Meanwhile, the piezoelectric protector is an
additional mechanism to avoid piezoelectric damage due to excessive
unidirectional compressive force as a result of an unpredictable uneven road.
It uses springs as the main component for regulating the pressure that deforms
the piezoelectric.
Figure 1 System: (a) suspension
[Adapted from www.pakwheels.com
(Ali, 2015)], (b) PEH, (c)
diagram block of modeling
2.2. System Modelling
The model of the overall system in Figure 1a comprises three main
subsystems: the dynamics of the bridge, the vehicle, and the PEH. In this
subsection, each will be detailed, and
the parameter values of the respective subsystems will be tabulated afterward.
2.2.1. Modelling
of Force Magnification Mechanism
Figure 2 shows the overall structure and working principle of the proposed force magnification mechanism, which is the main subsystem of the PEH. The spring force F generated by the vehicle suspension's vibration is transmitted to the large piston, which moves the master cylinder and produces force F1. The force is then transferred to the fluid in the closed channel. The fluid will move the small piston and produce F2 in the caliper. The force F2 will deform the piezoelectric bar and generate electrical energy. In short, this mechanism applies Pascal’s Law (Equations 1-2). By taking into account the cross-sectional area of both pistons, A1 and A2, the value of F2 can then be calculated,
The ratio of cross-sectional area is denoted by np
= A2/A1 where np>1 so the excitation force
in the master cylinder into the caliper can be magnified. This magnified force
will deform the piezoelectric at the end of the piston in the caliper. By
taking the effect of friction force between piston and cylinder and working
fluid mass in the pressurized cylinder-piston system are not accounted for, the
ratio of the big piston of master cylinder S1 and
small piston of caliper S2 to the respective cross-sectional area A1
and A2 is,
Since the excitation force
exerted by the vehicle suspension system on the PEH is random, impulsive
impact force can occur anytime. It then becomes an important
consideration for PEH design. A novel design of a piezoelectric protector
mechanism is proposed to minimize physical damage. Figure 2 provides
the design concept and its components. If the magnitude of force F
approaches or exceeds the limit of compressive strength of piezoelectric
material, the linear spring will be compressed accordingly. The push rod then
sticks to the stopper and discharges to press the piezoelectric. Thus, the
piezoelectric will always be within its strength limit and a
safe mode.
2.2.2. Modelling
of PEH
Since the PEH is mounted
onto the existing vehicle’s suspension, it can be considered as two main
structures: super- and sub-structure. The former is a vehicle, while the latter
is a hydraulic system-based PEH. The piezoelectricity
cylinder-piston mechanism depicted in Figure 3a can
be simplified as a translational lumped mass and is shown in Figure 3b. It
consists of an equivalent mass meq, damping coefficient ceq,
and spring constant keq. Two external springs are from master
cylinder kt and piezoelectric protector ks.
If the piston thickness and its mass density, tcp, and are respectively defined, then the mass of the small
piston under pressurized working fluid can be computed using Equation 3,
A big piston deforms the piezoelectric transducer
in Figure 2c through piston extension where its spring constant is not
considered. Spring stiffness kpb of the big piston may be computed using Equation 4,
Considering the working fluid,
the small piston can be modeled as a spring on a mass. The equivalent spring stiffness keq can be calculated
using Equation 5.
Figure 2 Overall structure and working principle (a) proposed force
magnification mechanism (b) Proposed piezoelectric protector mechanism (c) Piezoelectric
bar
When the work done by the
spring force is converted into electricity, there is an equivalent electric
resistance. The electrical damping coefficient ceq can be derived as follows (Aouali et
al., 2021; Pasharavesh, Moheimani, and Dalir, 2020; Wu, Wang, and Xie, 2015; Xie and Wang, 2015),
Equation 6 contains three important variables: d33 is the piezoelectric strain
constant in the polling direction, ca is the electrical capacity of the piezoelectric bar, and f is the natural vibration frequency of the system.
Once the equivalent mass meq, spring constant keq, and damping coefficient ceq are obtained, the proposed PEH
results in a damped single-degree-of-freedom system subjected to the road
surface roughness. Considering the equivalent magnified force Fm(t) at the PEH as expressed in Equation 7, the electrical charge that can
be stored by the piezoelectric bar is calculated using Equation 8,
Figure
3 PEH
model (a) Cylinder-piston
mechanism (b) Equivalent model of the proposed PEH
Equation 7 and Figure 3b contain some important parameters: yv and ywt are displacements of the vehicle
body and wheel tire, respectively, in the area where the PEH is mounted, yeq is the displacement of the
PEH, and n is the magnification factor
(cross-sectional area ratio). The electrical current resulted by the piezoelectric bar can be calculated by deriving the electrical charge in Equation 8 with respect to time,
The electrical voltage
resulted by the piezoelectric bar can be found by dividing the electrical charge Qep in Equation 8 over electrical capacity of the piezoelectric
material ca,
Generated electrical power is
then obtained by multiplying the electrical current in Equation 9 and electrical voltage in Equation 10 with the number of piezoelectric
p,
Equations 8-11 reflect that the outputs of PEH are electrical parameters such as
electrical charge, current, voltage, and power. In particular, electrical
charge Qep is seen as a very
instrumental parameter and must be produced optimally. The RMS of the electric
power within a predefined time duration can be
then determined by using Equation 12,
2.2.3. Modelling
of Bridge Dynamics Traversed by a Mobile Half-Car Planar Model
Quarter-car model is the common model employed.
However, such a model type is considered inadequate for many realistic cases,
particularly for analyzing the total vehicle dynamics. In this paper, the
vehicle consisting of the driver and passenger is
modeled as a mobile half-car planar model, as depicted in Figure 4a. The vehicle moves on a bridge above the uneven road
surface. The case becomes transverse elastic deformation of the bridge
traversed by a mobile half-car planar model carrying the PEHs. They are modeled
in Figure 4b. In deriving the governing equations of motion, simplifications
and assumptions are defined:
1.
The
overall system is modeled in linear behavior.
2.
A mobile half-car planar model has six DoFs,
which consist of a body, two PEHs, two-wheel tires, a driver, and a passenger. The vehicle body
is constrained to have the vertical motion (bounce) and the angular motion
(pitch), where every wheel-tire bounces in its respective coordinate. Also, the driver and
the passenger are considered to have only their vertical oscillations.
3.
The PEH is mounted between the vehicle body and
the wheel-tire in front or rear positions.
4.
Passenger seats, suspension, and wheel-tire
systems are modeled as a combination of linear springs and viscous dampers
which are connected in parallel arrangements.
5.
The resilience and damping of the suspension
and wheel-tire systems are expected to be sufficient so as to be more realistic
models for simulation and analysis.
6.
The
wheel-tire system is assumed to be in contact with the surface of the uneven
road at all times.
To
derive the motion equations of the overall system, the energy method is
employed. By defining x as the axis along the length of the beam measured
from the left to right end support, and t
as the travel time, then y(x,t) can be
characterized as the vertical deformation of the bridge all the way of the
undeformed neural axis of the bridge as depicted by Figure 4b. The kinetic and
potential energies of the overall system in Figure 4a using linear strains
assumption are given by Equations 13-14, respectively. Both equations belong to
the bridge, vehicle body (bounce and pitch), PEH, wheel-tire (front and rear), driver, and passenger.
Parameter in
Equation 13 is the mass density per unit length of the uniform beam, EI in Equation 14 denotes the
flexural rigidity of the beam, while H(x) represents the Heaviside function. In particular,
Equation 14 contains variables
which point out the locations of the contact
points of the front and rear tires with the bridge surface.
Rayleigh’s dissipation function and generalized
force are expressed in Equations 16-18,
By considering the Galerkin approximation, y(x,t) is written in Equation 19, where presents mode shapes and qi(t) points out the generalized coordinates for the
elastic deflection of the beam element. Orthogonality conditions are given by Equation 20, where the term
denotes the Kronecker delta
for i,j=1,2,..,n,
Figure
4 Vehicle
system model (a) the bridge traversed by a mobile half-car planar model (b)
transverse elastic deformation of the bridge traversed by a mobile half-car
planar model
Defining the eight state variables as in Equation 21, Lagrange’s equations for those variables can be expressed in Equations 22-23,
Finally, motion equations of
the overall system can be derived in general forms,
1.
The
vertical motion (bounce) for the driver is given by,
2.
The
vertical motion (bounce) for the passenger is presented by,
3.
The
vertical motion (bounce) for the vehicle is defined as,
4.
The
vertical motion for the front PEH is,
5.
The
angular motion (pitch) for the vehicle can be expressed as,
6.
The
vertical motion for the rear PEH is,
7.
The
vertical motion for the front wheel-tire can be written as,
8.
The
vertical motion for the rear wheel-tire can be written as,
9.
The
equation motion of the bridge is,
Parameter ktot1 is equivalent spring
stiffness between shock-breaker with external spring of master cylinder kt, ktot2 is equivalent spring stiffness
between wheel-tires with external spring of piezoelectric protector ks while two coefficients D1 and D2 denote the predefined interval of the motion of the vehicle. The roughness of road surface (Wei and Taghavifar, 2017),
Gq(n0) indicates the roughness coefficient of the road surface, n0 refers to a reference spatial frequency with a value of 0.1 m-1, f0 is a minimal boundary frequency with a value of 0.0628 Hz, v(t) denotes the vehicle velocity, and w(t) presents a zero-mean white noise.
2.2.4. Numerical Solver
Equations 24-32 form a system of nine second-order
coupled differential equations. They could be written in the state-space model by converting all equations into
first-order differential equation systems. Consequently, state variables become
(2+(2·DOF)+n) as the following,
From Equation 34, the
system of first-order differential equations can be arranged in Equation 35.
Considering the computational time and accuracy, the time step is selected as 0.001 s. Consequently, the
displacements and velocities of the system at the time ti+1 can be arranged as in Equation 36. By assuming that
the system is in an equilibrium position at i=0 and t0=0 s, the initial conditions of all are equal to zero.
The proposed PEH's performance is evaluated using
important design factors: the ratio of piston cross-sectional area, vehicle velocity,
and road roughness coefficient. Dynamic responses of displacement, velocity,
and acceleration in all nodal coordinates of the half-car planar model,
particularly at the point of the PEH mounted on the vehicle suspension, are used.
For vehicle dynamics, the road roughness coefficient refers to ISO/TC108/SC2N67 (Wei and Taghavifar, 2017), in
which only the classes B, E, and H are used, with roughness coefficient (Gq(n0),
in cm3) are 64; 4,096; and 65,536 respectively. Meanwhile, Tables 1
and 2 list the beam and
vehicle parameters. Dimension and material properties of the PEH are listed in
Table 3. The harvested electric power is expressed in RMS value.
3.1. Dynamic Responses Analysis
Results are obtained by setting the numerical variables in simulations
such as: (1) a random Gaussian white noise with a zero mean shown in Figure 5a,
(2) road surface roughness of the car on the road in the class of B for 10
seconds are depicted in Figure 5b, (3) Two types of velocity are used in terms
of variable and constant velocities as, where the former is shown in Figure 6a,
and the latter is set to be constant of 30 m/s, (4) parameters of the bridge, vehicle, and PEH are
based on Tables 1-3. Dynamic displacements are displayed in Figures 6b. Each figure compares the
displacement of respective subsystems under both velocities. However, it should
be noted that the values are selected only to show the dynamic characteristics.
Any arbitrary values can be chosen as long as the time trajectory of the vehicle
moving on the bridge is sufficient. Figure 7 reveals that the developed motion equations with
the numerical solver can capture the dynamics of the overall system. The
dynamic displacement obtained from variable and constant velocities is
different. An amplification factor is produced when the maximum value of each
displacement is compared. The ratio is averagely found around 1.23. It can be a
variation if the trajectory profile is varied accordingly. However, those figures
are intended to demonstrate the effect of velocity on the generated electrical
power of the proposed PEH model, as justified by Figure 8a.
Figure 5 Road
data (a) Gaussian white noise with zero mean
value (b) road surface roughness
Figure 6
Vehicle and bridge system (a) Trajectory profile for vehicle (b) Bridge
displacements
3.2. Parametric
Study for PEH
Three key design parameters
are chosen: vehicle speed variations,
road roughness coefficient, and ratio of the cross-sectional area of the
piston. Each variation is tested with three white noise time series to check
the robustness of the generated electric power. The white noise has a similar
mean value with different intensities, shown in Figure 8b respectively. The
first parametric study involves variations in vehicle velocity and its effect
on the harvested electric power, while keeping the road roughness coefficient
in the C class and maintaining a piston cross-sectional area ratio of 4. The
piezoelectric bar and the cylinder-piston dimensions are based on Tables 2-3.
The results show that the highest RMS of the generated power is 135 W. From Figure 9a, it can be seen that the
increase in vehicle velocity is followed by the increase of Prms.
The increment has a linear form. This finding owes to the fact that an increase
in velocity leads to an increase in dynamic displacements of the bridge and
suspension system, respectively. As a result, the dynamic displacement of the
equivalent model of the cylinder-piston mechanism and piezoelectric bar (PEH)
in Figure 3, either in the front or rear parts increases correspondingly. Those
increments correspond to the increase in charge, voltage, current, and
generated electric power of the PEH as indicated by Equations 9-12. Under three
white noise time series, the difference slightly deviates within 6% for the
generated electrical power. Thus, the proposed PEH model is less sensitive to
noise variances.
In
the next case, we examine variations in the road roughness coefficient while
keeping the vehicle velocity at 40 m/s and the cross-sectional area ratio at 4.
Road-roughness coefficients are based on ISO/TC108/SC2N67 (Class A-H).
Piezoelectric bar dimensions and piston-cylinder dimensions are still based on
Table 3. The results are displayed in Figure 9b. Similar to the previous
variation, an increase in the road roughness coefficient results in an increase
in the RMS of the electric power generated by the proposed PEH. However, this
increment follows a nonlinear form. The results show that the highest RMS of
the generated power is 230 W. However, this value is only found on a very
rough road. Such a road may be found as off-road, which is not common as a
public road. City road is commonly found in the range of class A to class D so
the road-roughness coefficients are considered in those ranges. In this
variation, the proposed PEH model is also less sensitive to noise variations.
The difference is within 7.5%.
Table 1 Beam parameters
|
Parameter |
Value |
|
Beam length (m) |
150 |
|
Mass density (kg/m3) |
20,000 |
|
Modulus of elasticity
of the beam (N/m2) |
2.07e11 |
|
Moment of inertia (m4)
|
0.261 |
|
Damping Coefficient
(N.s/m) |
2,625 |
Table 2 Vehicle parameters
Table 3 Property
and dimension of a piezoelectric bar (Piezo,
n.d.)]
The last case is variations of
piston cross-sectional area ratio to the harvested electric power by keeping
the vehicle velocity of 30 m/s, and road roughness coefficients in the class of
C. The results are displayed in Figure 9c. A nonlinear relation between the RMS
of the electric power generated by the proposed PEH and the piston cross-sectional
area ratio is found. The results show that the highest RMS of the generated
power is 93.5 W under piezoelectric bar and cylinder-piston dimensions in Table
2. This is to be expected since the increase of cross-sectional area ratio np decreases the deflection of the
PEH. This can be referred to as magnified force Fm(t) in Equation 7.
Since the force increases
with the ratio of n, then
the Prms
increases up to a certain limit. When the ratio of np is at higher values, the equivalent damping
coefficient ceq becomes predominantly, and the Prms decrease according to Equation 6. Hence, the optimum
value of np is selected to be 4, which can still be
accommodated in the design. For this variation, the proposed PEH model also
seems less sensitive to the noise variations as in the previous case. The
difference is found within 8.7% for the generated electrical power. This result
suggests that the proposed PEH is robust due to the deviation being relatively low to the
variations of white noise as an environmental factor.
Figure 7 Dynamic displacements of (a) vehicle body (b) front
tire (c) rear tire (d) PEH
Figure 8 Harvested
energy (a) Generated electric power (b) White noise time series
![]()
Figure 9 RMS
of generated electric power under
variation of (a) vehicle velocity (b) road class (c) piston cross-sectional area ratio
In this paper, a novel design of a PEH
for a vehicle suspension system has been developed. The structural dynamics of the
bridge, vehicle in terms of half-car model, and PEH system are characterized to
calculate the RMS of generated electric power. The finding results show that
the RMS of generated electric power increases with an increase in the velocity of vehicles, the ratio of the
cross-sectional area of the piston cylinder, and the road roughness
coefficient. The increment has a linear form for vehicle velocity variation and
a nonlinear form for the last two variations. The electric power can be harvested up to 67.5 W for a
PEH with a span of 150 m of the bridge, a velocity of 40 m/s, and a vehicle
mass of 2,691.6 kg. Based
on the findings, it is possible to harvest a higher power by increasing the
number of PEHs, high-capacity type piezoelectric transducer, the size of the
vehicle and speed, the number of passengers, and other parametric designs as
long as the vehicle and PEH are safe. However, experimental work is envisaged
for future work.
Financial support from Electronics and Information Research Organization
under contract: SK IPT no. 2/III/HK/2022 and facility from Research Centre for Smart Mechatronics, National
Research and Innovation Agency (BRIN) are greatly appreciated.
Akbar, M., Ramadhani,
M.J., Izzuddin, M.A., Gunawan, L., Sasongko, R.A., Kusni, M., Curiel-Sosa,
J.L., 2022. Evaluation on Piezoaeroelastic Energy Harvesting Potential of A Jet
Transport Aircraft Wing with Multiphase Composite by means of Iterative Finite
Element Method. International Journal of Technology, Volume 13(4), pp.
803–815
Alhumaid, S., Hess, D.,
Guldiken, R., 2022. A Noncontact Magneto–Piezo Harvester-Based Vehicle
Regenerative Suspension System: An Experimental Study. Energies, Volume 15,
p. 4476
Ali, A., 2015. Comparison Between Pakistani Corolla and
Civic’s Suspension: What’s The Difference? Available Online at: https://www.pakwheels.com/blog/comparison-between-pakistani-corolla-and-civics-suspension-whats-the-difference/#:~:text=Bo
th%20Civic%20and%20Corolla%20use,wishbone%20aka%20double%20A%20suspension, Accessed on June 14, 2021
Al-Yafeai, D., Darabseh, T., Mourad, A.-H.I., 2020.
Energy Harvesting from Car Suspension System Subjected to Random Excitation. In:
2020 Advances in Science and Engineering Technology International Conferences
(ASET). Presented at the 2020 Advances in Science and Engineering Technology
International Conferences (ASET), IEEE, Dubai, United Arab Emirates, pp. 1–5
Aouali, K., Kacem, N., Bouhaddi, N., Haddar, M.,
2021. On the Optimization of a Multimodal Electromagnetic Vibration Energy
Harvester Using Mode Localization and Nonlinear Dynamics. Actuators,
Volume 10, p. 25
Azangbebil, H., Djokoto,
S.S., Chaab, A.A., Dragasius, E., 2019. A Study of Nonlinear Piezoelectric Energy Harvester
with Variable Damping Using Thin Film MR Fluid. IFAC Papers OnLine, Volume 52-10, pp.
394–399
Chen, Y., Zhang, H., Zhang, Y., Li, C., Yang, Q.,
Zheng, H., Lü, C., 2016. Mechanical Energy Harvesting from Road Pavements Under
Vehicular Load Using Embedded Piezoelectric Elements. Journal of Applied
Mechanics, Volume 83, p. 081001
Darabseh, T., Al-Yafeai, D., Mourad, A.I.,
Almaskari, F., 2021. Piezoelectric Method?Based Harvested Energy Evaluation
from Car Suspension System: Simulation and Experimental Study. Energy
Science & Engineering, Volume 9, pp. 417–433
Du, R., Xiao, J., Chang,
S., Zhao, L., Wei, K., Zhang, W., Zou, H., 2023. Mechanical Energy Harvesting
in Traffic Environment and its Application in Smart Transportation. Journal
of Physics D: Applied Physics, Volume 56, p. 373002
Elgamal, M.A., Elgamal, H., Kouritem, S.A., 2024.
Optimized Multi-Frequency Nonlinear Broadband Piezoelectric Energy Harvester
Designs. Scientific Reports, Volume 14, p. 11401
Ghormare, P., 2022.
Development of Energy Harvesting Device to Utilize the Vibrational Energy of
the Vehicle Suspension Systems. In: The 2nd International Conference on
Innovative Research in Renewable Energy Technologies (IRRET 2022), MDPI,
p. 10
Hendrowati, W., Guntur, H.L., Sutantra, I.N., 2012.
Design, Modeling and Analysis of Implementing a Multilayer Piezoelectric
Vibration Energy Harvesting Mechanism in the Vehicle Suspension. Engineering,
Volume 4, pp. 728–738
Jeon, Y.B., Sood, R., Jeong, J.-h., Kim, S.-G.,
2005. MEMS Power Generator with Transverse Mode Thin Film PZT. Sensors and
Actuators A: Physical, Volume 122, pp. 16–22
Kulkarni, H., Zohaib, K.,
Khusru, A., Shravan Aiyappa, K., 2018. Application of Piezoelectric Technology In
Automotive Systems. Materials Today: Proceedings, Volume 5, pp. 21299–21304
Lafarge, B., Delebarre, C., Grondel, S., Curea, O.,
Hacala, A., 2015. Analysis and Optimization of a Piezoelectric Harvester on a
Car Damper. Physics Procedia, Volume 70, pp. 970–973
Lafarge, B., Grondel,
S., Delebarre, C., Cattan, E., 2018. A Validated Simulation of Energy
Harvesting with Piezoelectric Cantilever Beams on a Vehicle Suspension Using
Bond Graph Approach. Mechatronics, Volume 53, pp. 202–214
Li, Z., Peng, Y., Xu, A.,
Peng, J., Xin, L., Wang, M., Luo, J., Xie, S., Pu, H., 2021. Harnessing Energy Form
Suspension Systems of Oceanic Vehicles with High-Performance Piezoelectric
Generators. Energy, Volume 228, pp. 1–14
Morangueira, Y.L.A.,
Pereira, J.C.C., 2020. Energy
Harvesting Assessment with A Coupled Full Car and Piezoelectric Model. Applied
Energy, Volume 210, pp. 1–13
Pan, P., Zhang, D., Nie, X., Chen, H., 2017. Development
of Piezoelectric Energy-Harvesting Tuned Mass Damper. Science China
Technological Sciences, Volume 60, pp. 467–478
Pasharavesh, A., Moheimani, R., Dalir, H., 2020.
Nonlinear Energy Harvesting from Vibratory Disc-Shaped Piezoelectric Laminates.
Theoretical and Applied Mechanics Letters, Volume 10, pp. 253–261
Piezo, n.d.
Specification of Large Piezo Stack.
Available Online
at: http://www.piezo.com/
prodstacks1.html,
Accessed on
April 10, 2020
Sheng, W., Xiang, H., Zhang, Z., Yuan, X., 2022.
High-Efficiency Piezoelectric Energy Harvester for Vehicle-Induced Bridge
Vibrations: Theory and Experiment. Composite Structures, Volume 299, p.
116040
Shin, Y.-H., Jung, I.,
Noh, M.-S., Kim, J. H., Choi, J.-Y., Kim, S., Kang, C.-Y., 2018. Piezoelectric
Polymer-Based Roadway Energy Harvesting via Displacement Amplification Module. Applied
Energy, Volume 216, pp. 741–750
Taghavifar, H.,
Rakheja, S., 2019. Parametric Analysis of the Potential of Energy Harvesting
from Commercial Vehicle Suspension System. In: Proceedings of the
Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,
Volume 233(11), pp. 2687–2700
Tao, J.X., Viet, N.V.,
Carpinteri, A., Wang, Q., 2017. Energy Harvesting from Wind by a Piezoelectric
Harvester. Engineering Structures, Volume 133, pp. 74–80
Tavares, R., Ruderman,
M., 2020. Energy Harvesting Using Piezoelectric Transducers for Suspension
Systems. Mechatronics, Volume 65, pp. 1–9
Tian, L., Shen, H., Yang, Q., Song, R., Bian, Y.,
2023. A Novel Outer-Inner Magnetic Two Degree-Of-Freedom Piezoelectric Energy
Harvester. Energy Conversion and Management, Volume 283, p. 116920
Touairi, S., Mabrouki,
M., 2021. Control and Modelling Evaluation of a Piezoelectric Harvester System.
International Journal of Dynamics and Control, Volume 9, pp. 1559–1575
Viet, N.V., Al-Qutayri,
M., Liew, K.M., Wang, Q., 2017. An Octo-Generator for Energy Harvesting Based
on The Piezoelectric Effect. Applied Ocean Research, Volume 64, pp.
128–134
Wang, M., Yin, P., Li,
Z., Sun, Y., Ding, J., Luo, J., Xie, S., Peng, Y., Pu, H., 2020. Harnessing
Energy from Spring Suspension Systems with A Compressive-Mode
High-Power-Density Piezoelectric Transducer. Energy Conversion and
Management, Volume 220, pp. 1–12
Wei, C., Taghavifar,
H., 2017. A Novel Approach to Energy Harvesting from Vehicle Suspension System:
Half-Vehicle Model. Energy, Volume 134, pp. 279–288
Wu, N., Wang, Q., Xie,
X., 2015. Ocean Wave Energy Harvesting with A Piezoelectric Coupled Buoy Structure.
Applied Ocean Research, Volume 50, pp. 110–118
Xie, L., Cai, S.,
Huang, G., Huang, L., Li, J., Li, X., 2020. On Energy Harvesting from a Vehicle
Damper. IEEE/ASME Transactions on Mechatronics, Volume 25(1), pp.
108–117
Xie, X.D., Wang, Q.,
2015. Energy Harvesting from a Vehicle Suspension System. Energy, Volume
86, pp. 385–392
Zhao, Z., Wang, T.,
Shi, J., Zhang, B., Zhang, R., Li, M., Wen, Y., 2019a. Analysis and Application
of The Piezoelectric Energy Harvester on Light Electric Logistics Vehicle Suspension
Systems. Energy Science & Engineering, Volume 7(6), pp. 2741–2755
Zhao, Z., Wang, T., Zhang, B., Shi, J., 2019b.
Energy Harvesting from Vehicle Suspension System by Piezoelectric Harvester. Mathematical
Problems in Engineering, pp. 1–10
