Optimal Design and Performance Analysis of Multiple Photovoltaic with Grid-Connected Commercial Load
Corresponding email: mdpauzi@utm.my
Published at : 10 Jul 2024
Volume : IJtech
Vol 15, No 4 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i4.6019
Jamahori, H.F., Abdullah, M.P., Ali, A., AlKassem, A., 2024. Optimal Design and Performance Analysis of Multiple Photovoltaic with Grid-Connected Commercial Load. International Journal of Technology. Volume 15(4), pp. 834-846
| Hanis Farhah Jamahori | Faculty of Engineering, Built Environment and IT, Mahsa University, 42610 Selangor, Malaysia 2Institute of Future Energy, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 Johor |
| Md Pauzi Abdullah | Institute of Future Energy, Faculty of Electrical Engineering, Universiti Teknologi Malaysia, 81310 Johor Bahru, Malaysia |
| Abid Ali | Interdisciplinary Institute of Technological Innovation (3IT), Université de Sherbrooke, 3000 Boulevard Université, Sherbrooke, J1K OA5 Québec, Canada |
| Abdulrahman AlKassem | Department of Electrical Engineering, Faculty of Engineering, Islamic University of Madinah, Madinah 42351, Saudi Arabia |
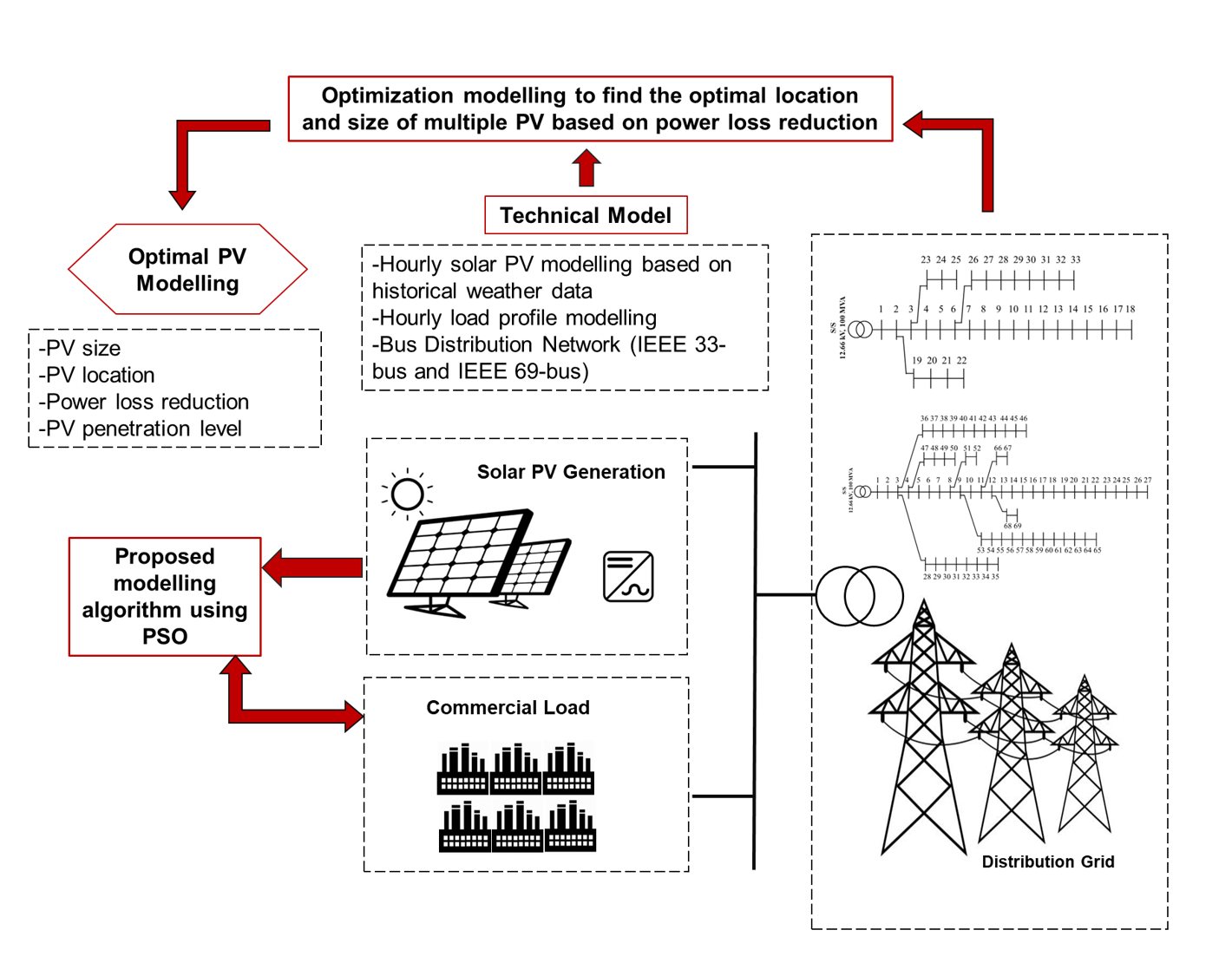
This study aimed to evaluate the potential of integrating
Photovoltaic (PV) with commercial load and examine the impact on distribution
networks. To estimate the hourly PV output power, 13 years of historical
weather data were used. Furthermore, a beta probability density function was
modeled to handle large amounts of data and generate a 24-hour predicted PV
curve. Particle Swarm Optimization (PSO) was used to determine the location and
size of multiple PV units, ranging from 1 to 3. PV performance was tested on
IEEE 33-bus and 69-bus test systems using time-varying commercial load, with
power loss index (PLI) set as the objective function. PV penetration level was
also calculated. The results showed a significant power loss reduction and PV
penetration levels when 3 PV units were integrated into the system compared to
a single PV unit. Specifically, the power loss reduction improved from 32.71%
to 45.37% and 43.80% to 48.08%, producing PV penetration levels of 43.08% and
40.15% in 33-bus and 69-bus systems, respectively. The results indicated that
the integration of multiple PV units was better than the single PV integration.
The proposed model using PSO determined the impact of considering
weather-dependent PV generation simultaneously with time-varying loads. It also
provided knowledge to model the optimal location and sizing of multiple PV
units in the distribution networks based on the generated solar irradiance
patterns.
Commercial load; Historical weather data; Power loss; PV penetration; Particle swarm optimization
Distributed
generation (DG) integration has significantly increased in recent years and is
expected to continue expanding, playing a more prominent role in the future
energy market. DG offers several advantages when integrated into a distribution
system, significantly altering the parameters (Hassan et al., 2020; Lee et al., 2020; Kola, 2018). Moreover, some of the technical
benefits include reducing transmission losses when connected near the consumer
load, improving bus voltage profile and power quality, increasing system
security and reliability, reducing dependency on the grid operator,
1.1. Literature Review
Several studies have focused on planning DREG technologies in
distribution networks, with the aim of minimizing power losses and improving PV
penetration through optimization. Various optimization methods have been used
to determine the optimal size and location of DREG units in power systems,
focusing on reducing transmission power losses and improving voltage profiles. (Khenissi et al., 2021) proposed using PSO and GA methods to determine
the optimal location and size of PV units. The study found that PSO
outperformed GA in terms of convergence, reduced power loss, and better voltage
profile. Similarly, the proposed Adaptive Particle Swarm Optimization (APSO)
showed that APSO produced better accuracy, optimal solutions, and faster
convergence than Bee Colony Optimization (BCO) and Lightening Search Algorithm
(LSA). (Kumar, Nallagownden and Elamvazuthi,
2017) adopted a PSO
algorithm for the optimal placement and sizing of DG units in a distribution
system, with the aim of reducing power loss and improving voltage stability.
The results confirmed the efficacy and robustness of PSO for PV integration in
the distribution system. Furthermore, (Hassanzadeh
and Jalilian, 2018) used
PSO as a multi-objective optimization method for power loss reduction and
voltage improvement in multi-DG placements in radial distribution systems. The
results showed that PSO significantly reduced total losses of the distribution
system and improved the voltage profile, producing optimal solutions with fast
convergence. These studies generally showed that PSO not only saved costs but
also produced lower power losses and better voltage profiles than Tabu Search,
Hybrid, and GA.
Studies have examined DREG planning, focusing on time-varying DG
generation and loads. For instance, (Khan,
Malik, and Sajjad, 2018) conducted a comparative analysis of the impact of time-varying PV
generation on load models. Three years of solar irradiance data were used to
predict hourly PV output through a novel probabilistic generation modelling approach.
In addition, the optimal size and
location of PV units were determined based on (Khan and Malik, 2017), which applied PSO for similar purpose. (Ahmed et al., 2020) proposed using Salp Swarm Algorithm (SSA) in a 19-bus system to
optimize the location and size of wind-based DG for different time-varying
loads based on multi-objective functions. However, this study was limited due
to the use of pre-defined load models and inability to report the use of
historical weather data. (Hossain et
al., 2023) showed the
importance of determining the optimal size for PV combined with energy storage
to accommodate varying commercial loads. However, the analysis focused on the
economic aspects and did not consider the maximum PV power contribution to the
grid for various load users. This oversight raised concerns about potential
stress on the grid, necessitating a more comprehensive approach to balance
economic considerations with grid infrastructure impacts. (Jamahori, Abdullah, and Ali, 2023) found that optimizing PV
generation by considering historical weather-dependent data and time-varying
loads could effectively meet diverse load demands. However, the study was
limited to the installation of a single PV unit, potentially compromising the
attainment of optimal results and the determination of the most efficient PV
unit required in the distribution network.
Problem Formulation
2.1. Solar PV Modelling
Thirteen years
of hourly weather satellite data (Solcast, 2018) were
used
to forecast the average hourly irradiance and PV output power as well as evaluate the potential of PV integration
with
commercial loads in Malaysia (30821N,
1014113E). The location of Malaysia near the equatorial makes it a
perfect opportunity to utilize abundant solar energy
resources, with an average annual irradiance of 4-5 kWh/m2/day (Mohammad, Al-Kayiem,
and Aurybi, 2020). The historical data
collected were divided into 24-hour segments, each with
solar irradiance measured at specific
hours.
The mean (µ) and standard deviation for each hour were calculated based on the irradiance data
collected hourly over the 13 years. This facilitated the
determination of the probability of solar irradiance for each hour and the estimation of PV output. The Beta-PDF f(s)
is expressed using equation (1) as follows (Atwa et al., 2010):
where is a gamma function,
and
both parameters of equation (6) are derived using mean, µ and standard
deviation,
respectively using equation (2) (Atwa et al., 2010):
The probability
of solar irradiance,
2.2. PV Module Output
PV power is significantly influenced by temperature, climate and geographical factors,
and solar irradiance. The output of PVNET module,
where
2.3. Load Modelling
The following equations (10)-(11)
express the new active and reactive distribution load demand
2.4. Distribution Bus System
This study used a standard IEEE 33-bus and 69-bus test system, with each distribution bus having different load power and system losses. The rated voltage for both systems was 100 MVA and 12.66 kV. The total load demand and base power losses for 33-bus were 3.715 MW, 2.300 MVAr, and 211.20 kW, 143.03 kVAr, respectively. The total load demand and base power losses for 69-bus were 3.800 MW, 2.690 MVAr, and 224.95 kW, 102.14 kVAr, respectively (Kakueinejad et al., 2020; Nawaz and Tandon, 2018). Furthermore, both bus systems were assumed to serve as distribution power stations for commercial load areas, meaning that all connection points were considered commercial consumers. This study was limited to using historical weather data based on collected solar irradiation, acknowledging that the power output might vary depending on solar irradiation at a specific location. It was assumed that the distribution grid was connected to the commercial load areas.
Figure 1 The normalized
commercial load curve (Jamahori,
Abdullah and Ali, 2023)
2.5. Load Flow
Analysis
Assuming
2 buses,
where Rij is the branch
resistance and Xij is the branch
reactance between 2 buses. The base case (without PV) hourly active
and reactive power injection across any branches at each period can be calculated as a summation of effective k + 1th
where Pi
The addition of a new
power source affected the load flow in the
distribution system. Therefore, the new
active, PDNEW(k+1) and reactive,
where PD(K+1) and QD(K+1) are the actual active and reactive load power
at the effective bus, while PPV and QPV a is positive (+) when PV injects reactive power
and negative (-) when it consumes reactive power, and
Assuming the
solar PV unit is installed at
2.7.
Particle Swarm Optimization (PSO)
PSO algorithm-based random
particle generation aimed to achieve the best value of the fitness function by
updating the position and velocity. The basic principle of PSO works by using
the swarm's knowledge and experience to randomly direct particles across the
search space to find the best local and global solution, g_best based on their personal best solution,
p_best. The particles change by updating position and velocity using a weighted
acceleration, ?, at each iteration to accelerate toward the fitness function.
PSO updates each particle by comparing the best
fitness to the current
Figure 2 The flowchart of the optimization framework using PSO
PSO parameters were selected based on initial
suggestions from the year of development (1995), which proposed limiting the
population size to 20-50 particles. Larger swarms typically improved the
efficiency of the method for more complicated problems and practical
applications. While significantly smaller swarm sizes were suggested for the
majority of PSO variants regarding unimodal problems, hundreds of
particles/swarms would still perform optimally. PSO parameters for the
integration of multiple PV are shown in Table 1.
Table 1 PSO
Parameters for integration of multiple PV
3.1. Optimal
Location and Size of Multiple PV units
The simulation result for multiple PV integrations with commercial load
users in IEEE 33-bus and IEEE 69-bus are summarized
in Tables 2 and 3, respectively. Based on the
optimization, the results showed that the
optimal PV sizing for the commercial load users differed
significantly in
both distribution networks. This was mainly due to the optimal
location and power demand in each bus system.
Tabel 2 Summary of multiple PV optimization
results in IEEE 33-Bus
|
Parameters |
Without PV |
1PV |
2PV |
3PV |
|
PV Location @ PV Size (MW) |
|
6 @ 4.57 |
12 @ 1.71 30 @ 2.08 |
14 @ 1.41 24 @ 1.75, 30 @ 1.75 |
|
Total PV Size (MW) |
|
4.57 |
3.79 |
4.91 |
|
PLoss (kW) |
1952.14 |
1313.54 |
1158.36 |
1066.38 |
|
PLoss Reduction, % |
|
32.71 |
40.66 |
45.37 |
|
QLoss (kVAr) |
1322.56 |
931.81 |
789.84 |
729.95 |
|
QLoss Reduction, % |
|
29.54 |
40.28 |
44.81 |
|
PV Penetration, % |
|
40.15 |
33.29 |
43.08 |
Tabel
3 Summary of
multiple PV optimization results in IEEE 69-Bus
|
Parameters |
Without PV |
1PV |
2PV |
3PV |
|
PV Location @ PV Size (MW) |
|
61 @ 3.35 |
18 @ 0.99 61 @ 3.19 |
11 @ 0.91 17 @ 0.72 61 @ 3.04 |
|
Total PV Size (MW) |
|
3.35 |
4.18 |
4.67 |
|
PLoss (kW) |
2074.32 |
1165.83 |
1091.18 |
1076.94 |
|
PLoss Reduction, % |
|
43.80 |
47.40 |
48.08 |
|
QLoss (kVAr) |
943.79 |
548.60 |
518.76 |
512.78 |
|
QLoss Reduction, % |
|
41.87 |
45.03 |
45.67 |
|
PV Penetration, % |
|
28.72 |
35.90 |
40.15 |
For IEEE 33-bus, the
optimal PV integration for a single PV was at bus 6 with
a size of 4.57 MW, while 2 PV units were at bus 12 and
30, respectively, with a size of 1.71 MW and 2.08 MW. The optimal location and
sizing of 3 PV units were at bus 14, 24,
and 30, with PV sizes of 1.41 MW, 1.75 MW, and 1.75 MW, respectively. In IEEE
69-bus, the optimal PV integration for a single PV was at bus 61 with
the size of 3.35 MW, while 2 PV units were at buses 18 and
61, respectively, with the size of 0.99 MW and 3.19 MW. The optimal location
and sizing of 3 PV units were at buses 11,
17, and 61, with PV sizes of 0.91 MW, 0.72 MW, and 3.04 MW, respectively. The
cumulative PV sizes for 1, 2, and 3 PV units were 4.57 MW,
3.79 MW, and 4.91 MW, respectively, for IEEE 33-bus and 3.35 MW, 4.18 MW, and
4.67 MW, respectively, for IEEE 69-bus. The
results showed that the average total PV size was larger when integrated with commercial load users in 33-bus compared to
69-bus system.
Figure
3 presents the expected PV output from Equation (9) and commercial demand
consumption for both systems using Equations (10)
and (11). Furthermore, maximum PV production and load consumption
occurred concurrently during the day, following the solar PV production, which
peaked at noon and was low in the
morning and evening.
Figure
3 Expected PV
output with commercial demand (a) IEEE 33-Bus; and (b) IEEE 69-Bus
Since the
system operated as an integrated grid system, the grid served
the remaining load consumption when PV power was
unavailable
or insufficient to supply the load. On the other hand, the highest PV output was
observed when 3 PV units were integrated
into both bus systems. The expected PV output was lowest with
2 PV in 33-bus and 1 PV unit in 69-bus system. While
the
varying lowest PV size
between both
buses did not affect the overall power losses, it
affected the overall PV penetration. Further
discussion on PV penetration level and power loss reduction was provided in the next sub-section.
3.2. Impact on PV Penetration
PV
penetration level is the total expected PV output (MW) ratio to the total load
demand consumed during the day (MW). A high
penetration level shows that PV production is
sufficient to provide power to meet the load demand. PV penetration results are presented in Figure 4. Based
on the
results, PV penetration levels for 1, 2, and 3 PV units in 33-bus and 69-bus were 40.15%,
33.29%, 43.08%, and 28.72%, 35.90%, 40.15%, respectively.
Figure 4 Penetration level for
multiple PV integration
The penetration level
increased significantly with load demand in 69-bus as the number of installed
PV increased, while the difference in penetration level between 1 PV and 3 PV
in 33-bus was insignificant. The maximum PV penetration was
recorded when 3 PV units were integrated
with commercial load in 33-bus, and the least being 1
unit integrated into 69-bus system. As mentioned, the optimum size of PV was subjected to
power loss minimization. Since power loss in
the distribution system depended on the load of each model, the size of PV
units in each case varied accordingly.
The cumulative sizes of PV in MW for each load model considering single and
multiple PV units for the two distribution systems are presented in Tables 2 and 3. For 33-bus
system, the impact of 2 PV units on the total size of PV in MW was the most
optimal compared to the installation of 1 and 3 PV units. On the other hand,
for 69-bus distribution system, the impact of 1 PV unit on the total size of PV in MW was more optimal
than the installation of 2 and 3 PV units. Therefore, the penetration of PV units in the
distribution networks varied and depended on the size of PV in distribution networks.
3.3. Impact on
Power Losses
The power loss
for multiple PV integration in both buses is presented in Figure
5.
The power loss reduction showed promising results after multiple PV units were
integrated into both bus systems. Specifically, the power loss for
1, 2, and 3 PV units in 33-bus and 69-bus were 32.71%,
40.66%, 45.37%, and 43.80%, 47.40%, 48.08%, respectively. These power
losses were influenced by the total PV generated
during the day, the total load served at a specific
hour,
and the location and sizing of PV units. In addition,
the load demand variations in each bus directly affected
the
location for PV installation. This could be attributed to the typical installation of PV near areas with
the highest load demand and farther from the grid
supply to ensure continuous power supply while
minimizing voltage deviation and power loss. The reduction in power losses was more significant with multiple PV in 33-bus compared
to 69-bus system. The
installation of a third PV in 69-bus did not
significantly reduce the total power losses. Therefore, 3 PV units were more optimal to be installed for 33-bus, and
only 2 PV units were recommended for
time-varying commercial users in 69-bus system,
as the effect
of the third PV could be neglected. This was because the rate of improvement in distribution system
performance was primarily determined by the total
size of PV units.
Figure 5 Power loss for multiple PV
integration (a) IEEE 33-Bus; and (b) IEEE 69-Bus
The optimal location and size of 1 to
3 PV units were determined based on proximity to areas with the
highest load demand and distance from the grid supply. This ensured the additional sources from PV could continue to supply the load at a
different location. The power losses with multiple PV were affected by the total PV generated
during the day, the total load served at a specific hour, and the total PV sizing on the
individual location. In addition, the load demand variations in different bus systems
directly affected the location of installation. Integrating multiple PV units showed that beyond
installing 2 PV units, there was no significant impact on 69-bus system. However, installing 3 PV was significant in addressing the load demand in 33-bus system. The reduction in power losses was more
prominent within 33-bus
compared to 69-bus system. The power loss was influenced by the supply of power to the distribution networks and
depended on the size of
PV units. Larger PV sizes corresponded
with greater improvements in bus voltage magnitude. Nonetheless,
inadequate PV
sizing could lead to
additional power losses and suboptimal improvement of bus voltage profiles.
In conclusion, this study showed that modeling multiple PV units with
commercial load users at optimal size and location had varied impacts on the distribution system
performance. Furthermore, the integration of multiple PV units outperformed single PV integration, resulting in
improved power loss reduction from 32.71% to
45.37% and 43.80% to 48.08% in 33-bus and 69-bus systems, respectively. This integration
produced PV penetration levels of 43.08% and 40.15% in the respective bus systems. The proposed model not only assessed the impact of considering weather-dependent PV generation alongside time-varying loads but also provided insights into modeling the optimal location and sizing of multiple
PV units in distribution networks based on solar irradiance patterns. Moreover, this study showed the importance of considering load variations in designing a PV grid system to ensure optimal performance and
efficiency. By accounting for variations in load demand, PV system could be appropriately sized to match
varying load profiles,
preventing overgeneration during low-demand periods and ensuring sufficient electricity generation during peak hours.
This method maximized the utilization of renewable energy and helped to maintain grid stability and
reliability, ensuring consistent voltage levels, balanced power flow, and the
ability to respond swiftly to changes in demand or supply to minimize power losses. Therefore, considering load variations was essential for the successful and
resilient operation of PV grid system.
Ahmed,
A., Nadeem, M.F., Sajjad, I.A., Bo, R., Khan, I.A., 2020. Optimal Allocation of Wind DG with Time
Varying Voltage Dependent Loads Using Bio-Inspired: Salp Swarm Algorithm. In:
3rd International Conference on Computing, Mathematics and
Engineering Technologies (iCoMET)
Ali,
A., Nor, N. M., Ibrahim, T., Romlie, M.F., 2018. Sizing and Placement of Solar
Photovoltaic Plants by Using Time-Series Historical Weather Data. Journal of Renewable and Sustainable Energy,
Volume 10(2), p. 023702
Atwa,
Y.M., El-Saadany, E.F., Salama, M.M.A., Seethapathy, R., 2010. Optimal Renewable
Resources Mix for Distribution System Energy Loss Minimization. IEEE Transactions on Power Systems, Volume 25(1), pp. 360–370
Bhambri,
S., Kumawat, M., Shrivastava, V., Agarwal, U., Jain, N.K., 2023. The Energy
Mix: An Emerging Trend in Distribution System. Optimal Planning and Operation of Distributed Energy Resources.
Spinger
Biswas,
P.P., Mallipeddi, R., Suganthan, P.N., Amaratunga, G.A.J., 2017. A Multiobjective
Approach for Optimal Placement and Sizing of Distributed Generators and
Capacitors in Distribution Network. Applied
Soft Computing, Volume 60, pp. 268–280
Board,
T.C., 2022. Global Economic Outlook. Available onlie at:
https://www.conference-board.org/topics/global-economic-outlook, Accessed on Agustus
31, 2022
Diwania,
S., Agrawal, S., Siddiqui, A.S., Singh, S., 2020. Photovoltaic–thermal (PV/T) Technology:
A Comprehensive Review on Applications and Its Advancement. International Journal of Energy and
Environmental Engineering, Volume 11(1),
pp. 33–54
Hassan,
A.S., Othman, E.A., Bendary, F.M., Ebrahim, M.A., 2020. Optimal Integration of
Distributed Generation Resources in Active Distribution Networks for
Techno-Economic Benefits. Energy Reports,
Volume 6, pp. 3462–3471
HassanzadehFard,
H., Jalilian, A., 2018. Optimal Sizing and Siting of Renewable Energy Resources
in Distribution Systems Considering Time Varying Electrical/Heating/Cooling
Loads Using PSO Algorithm. International
Journal of Green Energy, Volume 15(2),
pp. 113–128
Hossain,
J., Kadir, A.F.A., Shareef, H., Manojkumar, R., Saeed, N., Hanafi, A.N., 2023.
A Grid-Connected Optimal Hybrid PV-BES System Sizing for Malaysian Commercial
Buildings. Sustainability, Volume 15(13), p. 10564
IRENA,
2022. Latest Trend in Renewable Energy. Available online at
https://www.irena.org/Statistics/View-Data-by-Topic/Capacity-and-Generation/Statistics-Time-Series,
Accessed on August 31, 2022
Jamahori,
H.F., Abdullah, M.P., Ali, A., 2021. Integration
of PV Distributed Renewable Energy Generation into Distribution System using
Time-Varying Weather and Load Data. In: IEEE 19th Student Conference
on Research and Development (SCOReD)
Jamahori,
H.F., Abdullah, M.P., Ali, A., 2023. Impact and Evaluation of Optimized PV
Generation in the Distribution System with Varying Load Demands. Jurnal Teknologi, Volume 85(3), pp. 61–73
Jung,
C.-M., Pagidipala, S., Salkuti, S.R., 2024. Emerging Technologies for the
Integration of Renewable Energy, Energy Storage and Electric Vehicles. Energy and Environmental Aspects of Emerging
Technologies for Smart Grid. Springer
Kåberger,
T., 2018. Progress of Renewable Electricity Replacing Fossil Fuels. Global Energy Interconnection, Volume 1(1), pp. 48–52
Kakueinejad,
M., Heydari, A., Askari, M., Keynia, F., 2020. Optimal Planning for the
Development of Power System in Respect to Distributed Generations Based on the
Binary Dragonfly Algorithm. Applied
Sciences, Volume 10(14), p.
4795
Khan,
M.F.N., Malik, T.N., 2017. Probablistic Generation Model For Optimal Allocation
of PV DG In Distribution System with Time-Varying Load Models. Journal of Renewable and Sustainable Energy,
Volume 9(6), p. 065503
Khan,
M.F.N., Malik, T.N., Sajjad, I.A., 2018. Impact of Time Varying Load Models on PV
DG Planning. Journal of Renewable and
Sustainable Energy, Volume 10(3),
p. 035501
Khenissi,
I., Sellami, R., Fakhfakh, M.A., Neji, R., 2021. Power Loss Minimization Using
Optimal Placement and Sizing of Photovoltaic Distributed Generation Under Daily
Load Consumption Profile with PSO and GA Algorithms. Journal of Control, Automation and Electrical Systems, Volume 32, pp. 1317–1331
Kola,
S.S., 2018. A Review on Optimal Allocation and Sizing Techniques for DG in
Distribution Systems. International
Journal of Renewable Energy Research, Volume 8, pp. 1236–1256
Kumar,
C.M.S., Singh, S., Gupta, M.K., Nimdeo, Y.M., Raushan, R., Deorankar, A.V., Kumar,
T.M.A., Rout, P.K., Chanotiya, C.S., Pakhale, V.D., Nannaware,
A.S., 2023. Solar Energy: A Promising Renewable Source for Meeting Energy
Demand in Indian Agriculture Applications. Sustainable
Energy Technologies and Assessments, Volume
55, p. 102905
Kumar,
M., Nallagownden, P., Elamvazuthi, I., 2017. Multi-Objective PSO Based Optimal
Placement of Solar Power DG n Radial Distribution System. Journal of Electrical Systems, Volume 13, pp. 322–331
Lee,
J.Y., Verayiah, R., Ong, K.H., Ramasamy, A.K., Marsadek, M.B., 2020.
Distributed Generation: A Review on Current Energy Status, Grid-Interconnected
PQ Issues, and Implementation Constraints of DG in Malaysia. Energies, Volume 13(24), p. 6479
Lupangu,
C., Bansal, R.C., 2017. A Review of Technical Issues on the Development of
Solar Photovoltaic Systems. Renewable and
Sustainable Energy Reviews, Volume
73, pp. 950–965
Mohammad,
S.T., Al-Kayiem, H.H., Aurybi, M.A., Khlief, A.K., 2020. Measurement of Global
and direct Normal Solar Energy Radiation in Seri Iskandar and Comparison with
Other Cities of Malaysia. Case Studies in
Thermal Engineering, Volume 18, p.
100591
Nawaz,
S., Tandon, A., 2018. Power Loss Minimisation of Rural Feeder of Jaipur City by
Renewable-based DG Technologies. Australian
Journal of Electrical and Electronics Engineering, Volume 15, pp. 1–8
Nor,
N.M., Ali, A., Ibrahim, T., Romlie, M.F., 2018. Planning of Distributed
Renewable Energy Resources Using Genetic Algorithm. In: Sustainable Electrical Power Resources through Energy Optimization and
Future Engineering, S.A. Sulaiman, R. Kannan, S.A.A. Karim, N. Mohd Nor
(Eds.). Springer
Onibonoje,
M.O., Alegbeleye, O.O., Ojo, A.O., 2023. Control Design and Management of a
Distributed Energy Resources System. International
Journal of Technology, Volume 14(2),
pp. 291–319
Sánchez,
A.S., Junior, E.P., Gontijo, B.M., de Jong, P.,
dos Reis Nogueira, I.B., 2023. Replacing fossil fuels with renewable
energy in islands of high ecological value: The cases of Galápagos, Fernando de
Noronha, and Príncipe. Renewable and
Sustainable Energy Reviews, Volume
183, p. 113527
Saroji,
G., Berawi, M.A., Sari, M., Madyaningarum, N., Socaningrum, J.F., Susantono,
B., Woodhead, R., 2022. Optimizing the Development of Power Generation to
Increase the Utilization of Renewable Energy Sources. International Journal of Technology, Volume 13(7), pp. 1422–1431
Solar Power Europe, 2022. Global Market Outlook For
Solar Power 2022-2026. Available online
https://www.solarpowereurope.org/insights/market-outlooks/global-market-outlook-for-solar-power-2022,
Accessed data on July 25, 2022
Solcast,
2018. Solar Irradiance Data. Available online
https://solcast.com/solar-radiation-data/, Accessed on March 20, 2022
Zagloel,
T.Y.M., Harwahyu, R., Maknun, I.J., Kusrini, E., Whulanza, Y., 2023. Developing
Models and Tools for Exploring the Synergies between Energy Transition and the
Digital Economy. International Journal of
Technology, Volume 14(8),
pp. 291–319
Zhao,
L., Jerbi, H., Abbassi, R., Liu, B., Latifi, M., Nakamura, H., 2021. Sizing Renewable
Energy Systems With Energy Storage Systems Based Microgrids For Cost
Minimization Using Hybrid Shuffled Frog-Leaping and Pattern Search Algorithm. Sustainable Cities and Society, Volume 73, p. 103124
Zheng, D., Zhang, W., Alemu, S.N., S., Wang, P., Bitew, G.T.,
Wei, D., Yue, J., 2021. Chapter 1 - The concept of microgrid and related
terminologies. Microgrid Protection and
Control. Academic Press
