Implementation of Motion Detection Methods on Embedded Systems: A Performance Comparison

Recently, deploying machine learning methods and deep learning models to create an artificial intelligence system has gained huge interest. Several technologies, such as embedded GPU, ARM multicore processors, visual processor units VPUs, tensor processor units TPUs, and Field programmable arrays FPGAs, have been developed for this purpose. These processors and accelerators have been fitted on different edge boards and single computer boards SBCs. In this work, we present a performance comparison of background subtraction methods with many video resolutions on various technologies and boards. 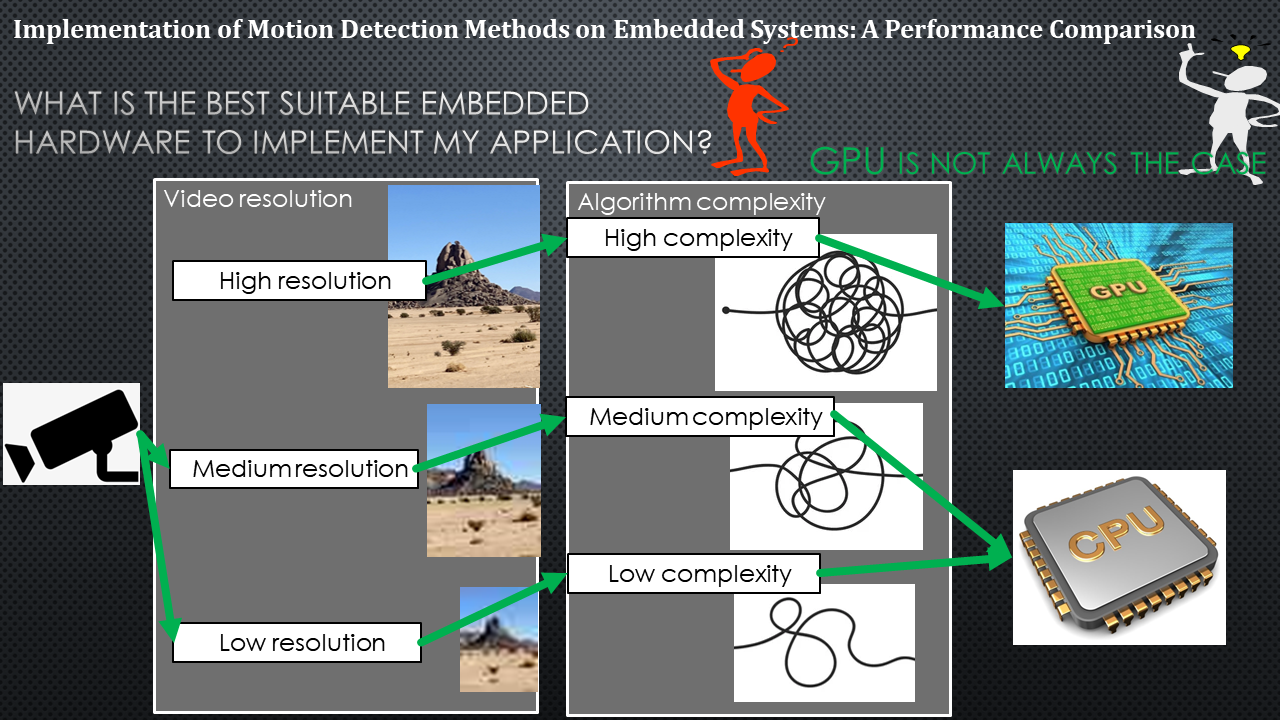The tested boards are equipped with different versions of ARM multicore processors and embedded GPUs. The aim is to overcome the lack of such studies on embedded devices and compare the performance of these recent hardware configurations. The implementation was achieved on ARM CPUs configuration using OpenCV and on embedded GPU using CUDA OpenCV. Results show that for high computational methods and high-resolution videos, the GPU is four times faster than the CPU. For low-mid computational methods or low-mid video resolution, the GPU performance is reduced due to GPU-CPU bottleneck transfer. This performance comparison enables the reader to better choose the suitable hardware for his mobile application.

ARM CPU; Embedded GPU; Embedded systems; Jetson boards; Motion detection; OpenCV CUDA

Background subtraction is known to be an essential task in video surveillance systems. Despite the significant advancement, especially with the appearance of supervised methods (Babaee et al., 2018; Lim et al., 2018; Wang, Luo, and Jodoin, 2017), this task still presents a challenging problem. Two concerns are involved: (1) the precision and the accuracy of the method and (2) the real-time aspect, which means the ability of this method to achieve the best results when implemented for real-life applications. In this case, a general-purpose processor GPP is insufficient to achieve excellent performance for such specific tasks. Moreover, the size and the high power consumption represent a drawback of this type of processor. Many alternatives exist, such as graphical processor units GPUs, field-programmable gate arrays FPGAs, parallel processors, and a multiprocessor system on chip MPSoC.

       In this context, (Song et al., 2016) proposed a background modeling method based on sequential images’ pixel-wise color histogram. The foreground pixels are grouped to separate blobs using a parallel-connected labeling algorithm. The implementation was done on the NVIDIA GeForce GT770 desktop graphics card with 4 GB RAM using the CUDA toolkit 5.5. They compared their method with GMM (Stauffer and Grimson, 1999) and the self-adaptive codebook (Shah, Deng, and Woodford, 2015). Results show that the proposed method has good segmentation and satisfies the requirement of real-time monitoring. (Liu et al., 2017) applied a background subtraction to detect and track multiple moving objects on wide-area motion imagery (WAMI) with a resolution of 2672×1200. The background is modeled using image averaging. The implementation was done via the cloud on multiple NVIDIA Kepler K20Xm GPUs. It was also compared with CPU and Apache Hadoop implementation. The results show that the Hadoop+GPU implementation is fourteen times faster than the CPU, seven times compared to GPU, and four times to CPU+Hadoop. These results are justified by the Hadoop framework’s capabilities that use the MapReduce programming model to distribute the computational algorithms parallelly on each cluster. (Jablonski and Przybylo, 2016) evaluated the Mixture of Gaussians algorithms on a GPU-based high-performance computing system. The authors used Open Computing Language OpenCL, a low-level programming framework for heterogeneous platforms (parallel CPUs, DSPs, FPGAs, and GPUs). The implementation was done on two hardware configurations: (1) HPC cluster node composed of NVIDIA Tesla M2090 and Intel Xeon E5645, and (2) PC Workstation with NVIDIA GeForce GTX670 and Intel I5 3570. The results show that the GPU implementation is eight times faster than the CPU of the first configuration and five times for the second configuration for the SD video format (720×576). (Nasr et al., 2017) implemented the recursive average filter for background modeling and subtraction. The authors used CUDA programming language and deployed their algorithm on NVIDIA desktop GPU, GeForce GT 525M. The results were compared to the Intel I3 CPU running at 2.2GHz and showed that the GPU is more than 160 times faster than the CPU. For more information about background subtraction methods and different platforms for implementation, we refer the reader to these papers (Mišic, Kovacev, and Tomaševic, 2022; Garcia-Garcia, Bouwmans, and Silva, 2020; Bariko et al., 2020; Janus, Kryjak, and Gorgon, 2020; Ahmed, Aljumah, and Ahmad, 2019; Imanullah, Yuniarno, and Sooai, 2019).

2.1. Euclidean distance method

        In this method (Sehairi et al., 2017), the foreground is generated by computing the Euclidean distance between two successive multichannel images (Equation 1).

where I_t(x,y) and I_t-1(x,y) represent the actual and the previous frame, respectively, and  corresponds to the red, green, and blue components in RGB color format. Then, the result is binarized using the threshold method to generate the foreground (Equation 2).

where T is the threshold value.

2.2. Running average filter method

        In this method, the background BG is constructed and updated by computing the average of N previous images. To overcome the problem of memory consumption, the background is calculated recursively using three methods, blind (3), selective (Bouwmans, 2014) (Equation 4), and fuzzy (Sigari, Mozayani, and Pourreza, 2008) (Equation 5):

where [0,1] is the learning rate, and _min is its minimum value. The foreground is then detected by applying the simple absolute difference between the actual frame and the constructed background (Equation 6).

        The initialization of this method is done with a clean scene that contains only static objects.

2.3. Zivkovic’s GMM method

        Based on Staufer’s and Grismon’s GMM algorithm, Zivkovic (Zivkovic, 2004) proposed a new technique to improve the time of execution of the original method. This technique estimates the number of Gaussians K for each pixel. For that, not just the parameters of these Gaussian distributions are updated, but also their numbers. In Staufer’s and Grismon’s GMM method, every pixel in the background is modeled by K Gaussian distribution, where K is constant. The aim is to consider dynamic backgrounds (lake or sea waves, tree shaking, flag flaps). Equation 7 gives the probability of observing the current pixel value X_t in the multichannel case:

where the weight w_i represents the frequency with which this i^th Gaussian has occurred in the past, u_i,t and u_i,t represent its mean and covariance matrix, and ? is given by:

        These distributions are learned over a series of training images and stored in descending order determined by the weight proportion and the variance w_k/w_k. Because of the costly implementation of the Expectation-Maximization EM algorithm, the online K-means approximation was used instead. For each new image I_t, each pixel X_t is compared to these stored Gaussians using Equation 9 or the Mahalanobis distance in the case of multichannel images (Equation 10):

where D is the deviation threshold.

If a match is found with Gaussian i, this means that this pixel X_t belongs to the background, and this Gaussian is updated to integrate the new information of the pixel as in Equations 11 & 12:

where  is the learning rate that adapts the model to slow temporal changes. is the second learning rate, also used as a modifier to reduce the influence of the outliers (Bouwmans, El Baf, and Vachon, 2008). has many ways to be set (Bouwmans, El Baf, and Vachon, 2008; Power and Schoonees, 2002; Stauffer and Grimson, 1999).

The parameters of the other unmatched Gaussians remain unchanged while their weights are reduced, as in Equation 13:

        If no match is found with any of these Gaussians, the model must be adapted rapidly to changes in the scene. This is done by replacing the least probable one, which has the lowest order, highest variance, and most negligible weight, with a new one whose mean corresponds to the value of the current pixel. Since all the Gaussians’ parameters have been changed, the order must be re-calculated, and the first B distributions satisfying the following equation are considered background.

where T is a threshold value that determines how much temporal history is attributed to the background. This operation aims to overcome the problem of the ghost effect. Finally, every pixel that did not match the background is considered foreground, Equation 9, 10.

        Not all the regions of the image are constantly dynamic. Therefore, not all pixels of the frames need K Gaussian distribution to be modeled. Hence, reducing the number of these Gaussians decreases the execution time efficiently. In this context, Zivkovic and Van Der Heijden (Zivkovic and Van Der Heijden, 2006) used Dirichlet prior with negative coefficients. As a result, the Gaussian component whose weights become negative is eliminated, and Equations 11 and 12 become, respectively:

where c_T is a complexity reduction parameter, it represents the minimum fraction of samples required to support the existence of a mode, set to be equal to 0.01 in (Zivkovic and Van Der Heijden, 2006)

Development Tools

3.1. Jetson development boards

        The first board used is the Jetson TK1. It is a single computer board SBC launched by NVIDIA in 2014. The board is based on a Tegra K1 System on Chip (SoC) that contains a quad ARM Cortex-A15 32 bits CPU and the GK20A NVIDIA GPU with 192 cores Kepler architecture supported by a fifth ARM Cortex-A15 for power and battery management. Its typical power consumption is between 1 to 5 watts, making it suitable for embedded systems applications. The board has 2GB of RAM and many inputs/outputs (HDMI, Ethernet, mini-PCIe, USB 3.0, audio, and GPIO). The Jetson TK1 board runs a specialized version of embedded Linux Ubuntu v14.04 LTS for Tegra SoCs, the Linux4Tegra L4T. This OS is installed using the Jetpack software development kit (SDK) that includes the OS image and many libraries, APIs, developer tools, and documentation (CUDA 6.5, OpenGL 4.4, VisionWorks, OpenCV4Tegra 2.14.13, CuDNN, Tegra Graphics developers…) and a more extensive set of GNU/Linux tools. The second board is the Jetson Nano, launched in 2019, a single computer board based on a system on module SOM and mounted on the Jetson Nano developer Kit carrier. The board includes a 64-bit CPU, the quad-core ARM Cortex-A57 that runs at 1.43GHz, and 128 cores of GPU with Maxwell architecture. The module has 4 GB 64-bit LPDDR4 RAM, an SD slot memory card, and an M.2 Key E interface. Its typical power consumption is between 5 and 10 watts. The carrier board has many input outputs (HDMI, display port, Ethernet, CSI interface, 4 USB 3.0, and 40 GPIO). The Jetson Nano board runs a recent version of Linux4Tegra based on Ubuntu 18.04.4 LTS. Like the Jetson TK1, the OS is installed using the Jetpack provided by NVIDIA, which contains recent versions of the same TK1 libraries, APIs, developer tools, and documentation (CUDA 10.0, OpenCV 4.1.1, CuDNN 7.6.3, TensorRT, Multimedia APIs, Python 2 and 3…). However, it should be noted that the pre-installed Jetpack OpenCV does not have CUDA support, and therefore it should be downloaded and re-built from the source.

3.2. Software development tools

3.2.1.  CUDA

CUDA is a parallel computing and application-programming interface (API) launched by NVIDIA in 2006 to speed up general computing on graphical processing units’ GPUs. It comprises two software layers; (1) CUDA Runtime API, considered a high-level API, and (2) CUDA Driver API, considered a low-level API. Unlike OpenCL, CUDA is used only for NVIDIA GPUs. However, CUDA supports many programming languages and frameworks such as C, C++, Python, Java, OpenACC (Open Accelerator), and OpenCL, making it easier for programmers familiar with standard programming languages than Dircet3D and OpenGL (Open Graphics Library). In addition, CUDA comes with many libraries such as CUDA Basic Linear Algebra Subroutine cuBLAS, NVIDIA Performance Primitives for 2D image and signal processing NPP, CUDA sparse matrix library cuSPARSE, CUDA Fast Fourier Transform cuFFT and CUDA random number generation cuRAND, (Nvidia, 2019).  

3.2.2.  OpenCV4Tegra

OpenCV4Tegra is a modified version of the Open Computer Vision library optimized by NVIDIA for its Tegra SoC and ARM NEON SIMD CPUs. The aim is to accelerate video and image processing on Android and Linux4Tegra mobile platforms. Fifty-nine functions were wholly re-designed to provide a speed-up between 1.6 to 32 times on Tegra K1 compared to regular OpenCV.

3.2.3.  OpenCV CUDA

Released in 2011, it is another rewritten version of OpenCV using CUDA to target NVIDIA GPUs. The library takes advantage of parallel computing to accelerate computer vision algorithms. It contains over 250 functions with a speed-up between 5 to 100 times compared to the desktop version. The OpenCV CUDA module is designed for ease of use. It differs from the CPU version in class, which starts with ‘cv::gpu’ in OpenCV 2 and ‘cv::cuda’ in OpenCV3 and higher versions instead of ‘cv::’. The data are stored in GPU memory using the instruction ‘cv::gpu::GpuMat’ instead of ‘cv::Mat’. The user should also enable CUDA support in his Cmake file.

4.    Implementation and Design

The development of background subtraction methods on Jetson TK1 GPU passes through a series of steps.

4.1. Loading video frames

The first step is to acquire images from the camera or load a video file from the SD memory card. Since the Linux4Tegra OS is installed on the host, this provides an abstraction layer between the hardware and software and resolves the problem linked to device driver definition and compatibility. It should be noted that Jetpack 21.4 includes a variant of the Ubuntu 14.04 version. Unfortunately, not all USB cameras are supported. A list of tested webcams is mentioned in (Elinux - Jetson/Cameras, 2022). Therefore, the user has to enable USB 3.0 for these types of cameras.

4.2. Transfer frames to the GPU

In this step, we have to upload images from the host (CPU) to the device (GPU) by calling the GPU header file. This step consumes time depending on the resolution and the color of video frames.

4.3. Background subtraction on GPU

For the Euclidean distance method, we start by creating a delay cell by copying and storing the frame I_t. Then, a Gaussian blur filter is applied to reduce the noise and smooth the image. Next, a second image I_t+1 is acquired and uploaded to the GPU; the same smoothing filter is applied to this frame. After that, the difference is computed on the GPU between these images, followed by a threshold operation. Finally, the second frame I_t+1 is stored as I_t.

For the running average filter method, the background is initialized using a scene that contains only static objects B₀, which is transferred from the host to the device. The recursive equation used to update the background is calculated using the CUDA version of the element operations (multiplication and addition) to accelerate computing. The same pre-processing is done by applying a Gaussian smoothing filter to each new image. The absolute difference is then computed on the GPU between the constructed background and the current frame, followed by threshold operation.

For the mixture of the Gaussians method, we start by defining its constructor on GPU and setting its parameters, such as the threshold D_i for the Mahalanobis distance test and the complexity reduction parameter c_T. Then, each new image is uploaded to GPU, and the same smoothing filter is applied to this frame and fitted to the MoG operator to generate the foreground mask. A threshold operation is applied to the generated foreground to eliminate pixel shadows.

4.4. Transfer the results back to the CPU

The generated foreground images must be downloaded from the device GPU to the host CPU to be displayed or stored on the SD memory. Figure 1 shows the outline of the GPU implementation of background subtraction techniques on the Jetson boards.

Figure 1 Background subtraction implementation on GPU

All the experiments are performed on Jetson TK1, Raspberry Pi 3, and Jetson Nano. The host side in Jetson TK1 is a 32bits quad-core ARM Cortex-A15 CPU. The implementations are done using the OpenCV4Tegra ver. 2.4. The device side is the GK20A GPU with Kepler architecture. The implementations are done using the OpenCV CUDA ver. 2.4. For Jetson Nano, the host is 64 bits quad-core ARM Cortex-A57, while the device is 128 GPU cores with Maxwell Architecture. The implementations are done on the host and the device using OpenCV 4.1.1. For comparison purposes, all background subtraction techniques are re-implemented and tested using OpenCV 4.1.1 on the Raspberry Pi 3 Model B single-board computer. The Raspberry Pi 3 includes the Broadcom SoC 2837, 64 bits quad-core ARM Cortex-A53 that runs at a speed of 1.2GHz, with 1 GB of RAM.

We chose four videos with different resolutions:

·         ‘Highway’ from the CDnet2014 dataset (Wang et al., 2014), the sequence contains 1700 frames with a resolution of 320×240. The video has a framerate of 25 fps.

·         ‘S2.L1 walking’ from the PETS2009 dataset (Ferryman and Shahrokni, 2009), the sequence contains 795 frames with a resolution of 768×576. The video has a framerate of 10 fps.

·         ‘Venice-2’ from the 2DMOT2015 dataset (Leal-Taixé et al., 2015), the sequence contains 600 frames with a resolution of 1920×1080. The video has a framerate of 25 fps.

·         ‘Venice-2 1280×720’ is a resized version of the previous video. The video has a framerate of 25 fps.

Figure 2 shows samples from the three videos and their corresponding foreground segmentation results. The results were obtained using the Zivkovic MoG method applied to the Jetson Nano CPU and Jetson Nano GPU. The parameters of the Zivkovic MoG were chosen as follows: the learning rate ?=0.005, the threshold on the squared Mahalanobis distance D?=16, the complexity reduction parameter c_T=0.05 and the threshold to remove the shadow of the objects Th=150.  Remarkably, the type of hardware implementation (CPU or GPU) does not affect the same method’s segmentation results.

Figure 2 Sample frames from each video in each dataset: (a) 850^th frame from the Highway video, CDnet2014, (b)700^th frame from the S2.L1 walking view_001, PETS2009 dataset, (c) 500^th frame from Venice-2, 2DMOT2015

Figure 3 shows the results of applying the three background subtraction methods (Euclidean distance ED, Running average filter method, Zivkovic Mixture of Gaussians MoG) on the Highway sequence (320×240). The results are presented in frames per second for each hardware. We note that the real-time constraint for low-resolution videos is easily reached for all four hardware configurations. We notice that the CPU is faster than the GPU for low computational methods, the Euclidean distance, and the running average filter method. This is due to the time needed for transferring frames from the CPU to GPU and back. In addition, the frame size is not significant enough to be computationally challenging for CPUs. For the mixture of Gaussians, we note that the GPU implementations are much faster than the CPUs. This is due to the computational load that presents this method and the parallelism processing linked to the GPUs’ design, which comes with 192 and 128 cores in TK1 and Nano, respectively. Between the three CPUs configurations, we remark that the results are approximately equal for TK1 and RPi3. However, Nano’s CPU is much faster than the last two configurations due to the recent ARM CPU version, which has a 64bits architecture and runs with a speed of 1.43GHz with 4GB RAM.

Figure 3 The computational time for each method applied to the Highway sequence

Figure 4 The computational time for each method applied to the S2.L1 walking sequence

Figure 4 shows the results of applying the three background subtraction methods to the S2.L1 walking sequence. For the two first methods (ED and RAF), we note that the real-time constraint is met for all the hardware configurations, and the Jetson Nano is the fastest of them both in CPU and GPU. The results for Jetson TK1 and Raspberry Pi3B are approximately close with a bit of edge to the Jetson TK1 GPU. On the contrary, the computational complexity of the MoG algorithm combined with the mass of data that carries a video makes the real-time aspect impossible to achieve for the late hardware CPUs. In this case, we also note that the CPU implementation on the Jetson Nano is faster than the Jetson TK1 GPU implementation. This is due to the CPU upgrade, the amount of memory available on the Nano compared to TK1, and the significant enhancement present in the recent OpenCV version 4.1.1 installed on the Nano compared to OpenCV 2.4.13 in the TK1.

Figure 5 and Figure 6 show the result of applying the three background subtraction methods on the Venice-2 sequences (1280×720 and 1920×1080, respectively). Unlike the previous experiences, the results, in this case, are not in real-time. This is due to the great mass of data that carries HD and Full-HD videos. In GPU, the calculation speed is amortized due to the operations of copying the images from CPU to GPU and then copying back the results; this is remarkably seen in low computational methods (ED and RAF). However, in the case of the MoG algorithm, the speed of the CPU’s configuration is drastically decreased.

Figure 5 The computational time for each method applied to the Venice-2 sequence with a resolution of 1280×720

Figure 6 The computational time for each method applied to the Venice-2 sequence with a resolution of 1920×1080

Table 1. compares our results with the results of (Bulat et al., 2014), who implemented the GMM method using OpenCL on a desktop GPU, the NVIDIA GeForce GT 645M GPU with 384 cores. It should be noted that this comparison is not fair since we compare a desktop GPU implementation with an embedded GPU implementation in which the consumption does not exceed 10W.

Table 1 Comparison between different GPU implementations of the GMM algorithms applied to HD and full HD videos

This comparative study concludes that the GPU implementation, compared to the CPU, does not achieve outstanding performance in all cases. For small-resolution videos and low computational methods, the additional steps of copying from CPU to GPU and vice versa decrease the speed of GPU’s implementation by creating a bottleneck. However, the GPU is an optimal choice for mid to high-resolution videos and complex algorithms due to the OpenCV CUDA’s optimized functions and the GPU’s parallelism. These features make GPU suitable for computational load applications such as video surveillance, tracking, Gaming, virtual reality, and augmented reality. However, we still need the CPU to load OS to capture and read images and display the results.

We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Jetson TK1 development board used for this research.

Ahmed, M.A., Aljumah, A., Ahmad, M.G., 2019. Design and Implementation of a Direct Memory Access Controller for Embedded Applications. International Journal of Technology, 10(2), pp. 309–319

Babaee, M., Dinh, D.T., Rigoll, G., 2018. A Deep Convolutional Neural Network for Video Sequence Background Subtraction. Pattern Recognition, Volume 76, pp. 635–649

Bariko, S., Klilou, A., Abounada, A., Arsalane, A., 2020. Efficient Implementation of Background Subtraction GMM method on Digital Signal Processor. In: 2020 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), pp. 1–5

Bouwmans, T., 2014. Traditional and Recent Approaches in Background Modeling for Foreground Detection: An overview. Computer Science Review, Volume 11, pp. 31–66

Bouwmans, T., El Baf, F.,  Vachon, B., 2008. Background Modeling Using Mixture of Gaussians for Foreground Detection-A Survey. Recent Patents on Computer Science, 1(3), pp. 219–237

Bulat, B., Kryjak, T., Gorgon, M., 2014. Implementation of Advanced Foreground Segmentation Algorithms GMM, Vibe and PBAS in FPGA and GPU–A Comparison. In: Computer Vision and Graphics: International Conference, ICCVG 2014, Warsaw, Poland, September 15-17, 2014

Elinux Embedded Linux, 2022. Jetson/Cameras. Available online at https://elinux.org/Jetson/Cameras, Accessed on April 17, 2023

Ferryman, J., Shahrokni, A., 2009. Pets2009: Dataset and Challenge. In: 2009 Twelfth IEEE International Workshop on Performance Evaluation of Tracking and Surveillance, pp. 1-6

Garcia-Garcia, B., Bouwmans, T., Silva, A.J.R., 2020. Background Subtraction in Real Applications: Challenges, Current Models and Future Directions. Computer Science Review, Volume 35, p. 100204

Imanullah, M., Yuniarno, E.M., Sooai, A.G., 2019. A Novel Approach in Low-cost Motion Capture System using Color Descriptor and Stereo Webcam. International Journal of Technology, Volume 10(5), pp. 942–952

Jab?o?ski, M., Przyby?o, J., 2016. Evaluation of MoG Video Segmentation on GPU-Based HPC System. Computing and Informatics, Volume 35(5), pp. 1141–1159

Janus, P., Kryjak, T., Gorgon, M., 2020. Foreground Object Segmentation in RGB–D Data Implemented on GPU. In: Advanced, Contemporary Control: Proceedings of KKA 2020—The 20th Polish Control Conference, ?ód?, Poland

Leal-Taixé, L., Milan, A., Reid, I., Roth, S., Schindler, K., 2015. Motchallenge 2015: Towards a Benchmark for Multi-Target Tracking. Computer Vision and Pattern Recognition. https://doi.org/10.48550/arXiv.1504.01942

Liu, K., Wei, S., Chen, Z., Jia, B., Chen, G., Ling, H., Sheaff, C., Blasch, E., 2017. A Real-Time High Performance Computation Architecture for Multiple Moving Target Tracking Based on Wide-Area Motion Imagery Via Cloud and Graphic Processing Units. Sensors, Volume 17(2), p. 356

Miši?, M., Kova?ev, P., Tomaševi?, M., 2022. Improving Performance of Background Subtraction on Mobile Devices: A Parallel Approach. Journal of Real-Time Image Processing, Volume 19(2), pp. 275–286

Nasr, M., Khemiri, R., Sayadi, F.E., Ouni, B., 2017. Parallel Implementation on a GPU of a Detection and Tracking Algorithm by Basic Background Subtraction. In: 2017 International Conference on Engineering & MIS

Nvidia, 2019. CUDA Toolkit Documentation v10. Available online at https://docs.nvidia.com/cuda/archive/10.2/, Accessed on April 17, 2023

Power, P.W., Schoonees, J.A., 2002. Understanding Background Mixture Models for Foreground Segmentation. In: Proceedings Image and Vision Computing New Zealand

Sehairi, K., Chouireb, F., Meunier, J., 2017. Comparative Study of Motion Detection Methods for Video Surveillance Systems. Journal of Electronic Imaging, Volume 26(2), p. 023025

Shah, M., Deng, J.D., Woodford, B.J., 2015. A Self-Adaptive CodeBook (SACB) Model for Real-Time Background Subtraction. Image and Vision Computing, Volume 38, pp. 52–64

Sigari, M.H., Mozayani, N., Pourreza, H., 2008. Fuzzy Running Average and Fuzzy Background Subtraction: Concepts and Application. International Journal of Computer Science and Network Security, Volume 8(2), pp. 138–143

Song, W., Tian, Y., Fong, S., Cho, K., Wang, W., Zhang, W., 2016. GPU-Accelerated Foreground Segmentation and Labeling for Real-Time Video Surveillance. Sustainability, Volume 8(10), p. 916

Stauffer, C., Grimson, W.E.L., 1999. Adaptive Background Mixture Models for Real-Time Tracking. In 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition

Wang, Y., Jodoin, P.M., Porikli, F., Konrad, J., Benezeth, Y., Ishwar, P., 2014. CDnet 2014: An Expanded Change Detection Benchmark Dataset. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops

Wang, Y., Luo, Z., Jodoin, P.M., 2017. Interactive Deep Learning Method For Segmenting Moving Objects. Pattern Recognition Letters, Volume 96, pp. 66–75

Zivkovic, Z., 2004. Improved Adaptive Gaussian Mixture Model for Background Subtraction. In: Proceedings of the 17^th International Conference on Pattern Recognition

Zivkovic, Z. and Van Der Heijden, F., 2006. Efficient adaptive density estimation per image pixel for the task of background subtraction. Pattern recognition letters, 27(7), pp.773-780.