Optimized Calibration Plan based on Gray Model GM(1,1) applied in Physical-Photometric and Chemical Laboratories Accredited by ISO/IEC 17025
Corresponding email: cavf1@alu.ua.es
Published at : 18 Sep 2024
Volume : IJtech
Vol 15, No 5 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i5.5938
Velásquez, C., Espín, F., Iturra, F., Chasi, C., 2024. Optimized Calibration Plan based on Gray Model GM(1,1) applied in Physical-Photometric and Chemical Laboratories Accredited by ISO/IEC 17025. International Journal of Technology. Volume 15(5), pp. 1438-1448
| Carlos Velásquez | 1. Dept. of Applied Mathematics, University of Alicante, Apdo. 99, 03080, Alicante, Spain 2. Modalidad en Línea, Universidad Central del Ecuador, Quito 170521 Ecuador 3. Instituto de Investigación |
| Francisco Espín | 1. Instituto de Investigación Geológico y Energético, Quito 170518, Ecuador. 2. Departamento de Luminotecnia, Luz y Visión, Universidad Nacional de Tucumán, San Miguel de Tucumán Tucumán T4000, Argen |
| Francisco Iturra | Instituto de Investigación Geológico y Energético, Quito 170518, Ecuador |
| Consuelo Chasi | Instituto de Investigación Geológico y Energético, Quito 170518, Ecuador |
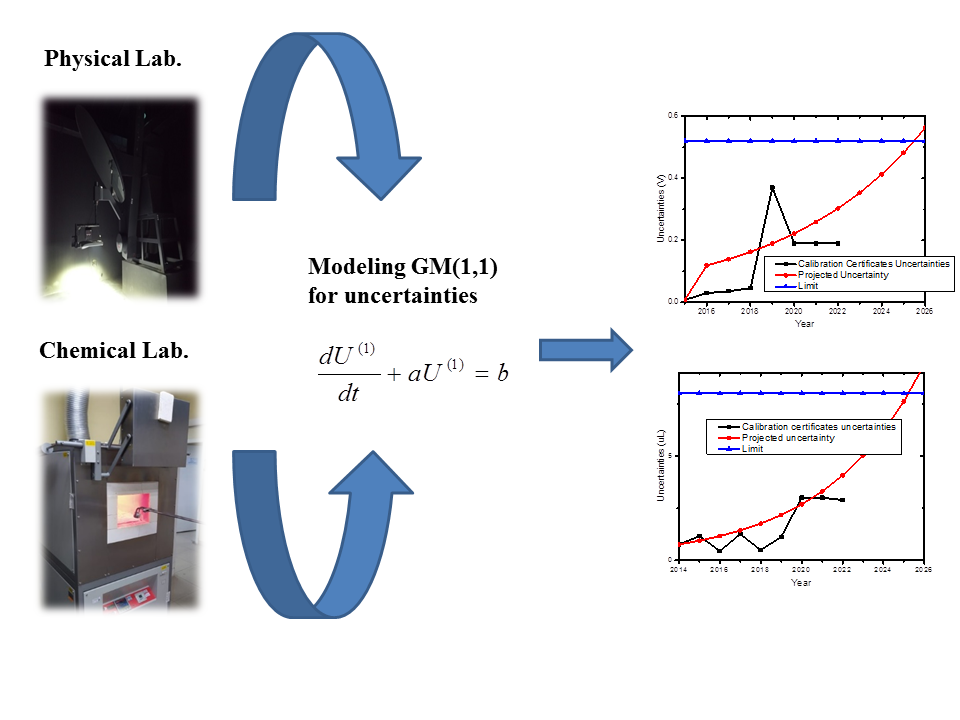
The competence of laboratories to perform testing and
calibration services for the industry is assured by the ISO/IEC 17025
accreditation. To comply with this standard, it is imperative to ensure
metrological traceability through the regular calibration of laboratory
equipment at defined schedules, which is time-consuming and demands significant
financial resources. The present work applies first-order gray models GM(1,1)
using calibration uncertainties to establish an optimized calibration plan that
considers different natural characteristics of laboratory activities, thus
providing technical support to ensure metrological traceability for a wide
range of laboratory tests. A luminous intensity distribution test on LED
luminaires and a fire assay method for determining gold were considered.
Applying the proposed approach, the outcoming times between calibrations were
longer than previously established, reducing 11% of the financial resources for
the physical-photometric laboratory and 54% for the chemical laboratory.
Therefore, it also increases the availability of calibrated pieces of
equipment. Moreover, results showed that this method suits physical and
chemical laboratory tests. In conclusion, this methodology could increase the
time between calibrations and reduce the financial resources needed while
maintaining technical competence or confidence in laboratory results.
Fire assay; Gray model; ISO/IEC 17025 accreditation; Luminous intensity; Uncertainties
The
ISO/IEC 17025:2017 standard "General
requirements for the competence of testing and calibration laboratories"
There are different ways of carrying out the laboratory calibration
program, usually adopted by guidelines suggested by the
International Laboratory Accreditation Cooperation and the International Organization of Legal Metrology in
ILAC G24 OIML D10 (Legal International Organization of Metrology, 2007).
Most laboratories apply year-to-year calibration and instrumental drift
calculation methods.
A
“dynamic calibration program” changes the paradigm of fixed calibration times.
It encourages laboratories to determine, through a series of evaluations, the
behavior of the measurement equipment and the most appropriate calibration
times (Silva and Rodrigues, 2013). The calibration time can
be determined by verifying the behavior of the measuring equipment between
calibrations or by estimating the variation of measurement uncertainty over
time
Estimating
the calibration time for measurement equipment is a complex issue that involves
economic risks when estimating time is too short (Pashnina, 2020) and technical risks when the estimated time
is excessively long (Gaber, 2021). An adequate procedure in
planning laboratory activities affects the production of its clients
Various
statistical approaches prove useful in determining a calibration interval (Butdee and Khanawapee, 2021; Velásquez et al., 2021b), with extensive research
conducted on the topic. Results expose methodologies used to define calibration
ranges, among them chain methodology, simple linear model, and decisional
model. Additionally, a large number of variables must be considered, such as
the maximum permissible errors required by the laboratory, frequency of use of
the equipment, type of application, robustness, other requirements determined
by manufacturers (Toteva, Slavov, and Vasileva, 2017), and other factors such as laboratory infrastructure
(electrical installations, environmental conditions), detect anomalies in
equipment (El-Hadad, Tan, and Tan, 2022) or the competence of the personnel operating
the equipment (Nugraha et al., 2022).
These
models have been generally applied to a single equipment or laboratory. This
work presents a new use of gray model study applied to physic and chemical
laboratories for its calibration ranges that have not been developed. The
first-order gray model GM(1,1) is a good alternative explored in some research.
It suggested that due to the characteristic of the technique to project values
whose nature of change is unknown (gray action)(Zeng, Ma, and Shi, 2020), it is advantageous to be
applied when projecting the changes over time of uncertainties of different
laboratory equipment (Lin and Liu, 2005). Applying this methodology allows adjusting
calibration intervals considering the reasons for a change of the equipment
with adequate predictions.
The
model GM(1,1) used in this research needs as a mathematical parameter the
calibration uncertainties of equipment involved in the complete test. A
calibration certificate usually provides much information to the laboratory,
mainly the correction and the uncertainty values
The
measured value could be adjusted by applying the certificate correction.
However, the uncertainty is related to the accuracy and repeatability status of
the equipment as well as the supplier's method of calibration. Through a
periodic calibration process of all the equipment whose measurements influence
the test results, values of bias and uncertainty are obtained, so that is why
the importance of ensuring correct calibrations and their intervals.
Due to
their nature, there are physical or chemical laboratories. In both, uncertainty
is the fundamental value representing the quality of an assay or a calibration
result. Its calculation and application are described through “The Guide to the
Expression of Uncertainty in Measurement,” also known as GUM
Even
though conceptually, the uncertainty term is always the same, in practice,
physical and chemical laboratories have differences in their estimates.
However, it is possible to apply an approximation of GM(1,1) regardless of the
nature of the activities of the laboratories.
In this
work, physical-photometric and chemical-accredited laboratories were the scopes
of application (Figure 1a and Figure 1b) (Velásquez et al.,
2023). In the case of the physical-photometric
laboratory, the assay to determine luminous intensities distribution in LED
luminaires employing a goniophotometer was analyzed. On the other hand, for
chemical laboratories (Juiña, Silva,
and Velásquez, 2024), the
analysis focused on the determination of gold concentration in minerals using
the 'fire assay' method combined with Atomic Absorption Spectrophotometry.
|
The based GM(1,1) methodology proposed was applied in two different
assays of different natures: physical-photometric and chemical. It is essential
to understand the annual cost of equipment calibration and the traceability
chain of each one. The traceability relationship between two laboratory
equipment in the chain (Figure 2, Figure 3) is ![]() . The
. The ![]() Represents if there is a
traceability transfer.
Represents if there is a
traceability transfer.
2.1. Traceability Chain for Physical-Photometric Laboratory
An accredited test in the
physical-photometric laboratory measures luminous intensities distribution in
LED luminaires using a C-type rotating mirror goniophotometer. The standard
methods for the test are CIE 121, "The
Photometry and Goniophotometer of Luminaires"
The test begins with stabilizing the
luminaire by turning it on for two hours at a constant voltage with a power
supply regulated at ±0.2%. Next, vector detection is developed through
spherical coordinates, where its direction will be given by the axial
(C-Planes) and azimuthal (Gamma Angles) angles and its magnitude by the light
intensity, describing the photometric volume of interest. Additionally, during
the test, a temperature of 25°C ± 1.2°C must be maintained because temperature
variation has an impact on the test
The
measurement of luminous intensities is absolute (cd) for LED luminaires. The
calibration of the goniophotometer is done with a work standard lamp. The work
standard lamp is traceable to the reference standard lamp with its electrical
parameters. The traceability chain is presented in Figure 2.
Figure 2 Traceability chain method of the test in the
physical-photometric laboratory
The photometric scheme has an
incandescent technology standard reference lamp (Z1), an incandescent
technology work lamp (Z2), a SENSING GMS-2000 Goniophotometer (Z3), and routine
test LED luminaires (Z10). The electrical magnitudes were supervised by a
Metrel MI 2892 Electrical Network Analyzer (Z2) and a Yokogawa WT310 Digital
Power Meter to detect voltage (Z5), current (Z6), and THDs (Z7). The
environmental conditions were measured with a verification equipment
Thermohygrometer TESTO 176P1 (Z8) and a routine measurement equipment
Thermohygrometer TESTO 174H (Z9).
2.2. Traceability Chain for Chemical Laboratory
The Chemical Laboratory performs
mineralogical and elemental tests in various geological matrices. Among other
trials, it determines gold by the “fire assay”, the reference technique for
gold quantification (Buitrón et al., 2021). It is based on the “ASTM E1335, Standard Test
Methods for Determination of Gold in Bullion by Fire Assay Cupellation
Analysis” and the “3111 Metals by Flame Atomic Absorption Spectrometry”. This
method is preferred over others due to its application to a broad spectrum of
samples, excellent versatility, and high accuracy (Buitrón et al., 2021). It is also considered that the nugget effect
is reduced due to the large amount of sample that can be used.
The equipment used for the assay are as
follows: Weights brand Mettler Toledo E2 type (Z1), a scale brand Precisa model
XB4200C (Z2), a scale brand Mettler Toledo model XP 205 (Z3), a scale brand
Citizen model CX 220 (Z4), a pipette of 500 brand Socorex (Z5), a pipette of
5000
brand Socorex (Z6), a pipette of 100
brand Socorex (Z7), a pipette
of 1000
brand Socorex (Z8), a dispenser of 10 mL brand Brand (Z9), certified
reference material of gold-containing minerals from Rocklabs (Z10), a certified
standard of gold from Inorganic Ventures (Z11), an Atomic Absorption
Spectrophotometer brand Perkin Elmer (Z12) two Thermo hygrometers brand
Traceable (Z13 and Z14), two
thermometers brand Fluke (Z15 and Z16), two muffles brand Incinerar (Z17 and
Z18), a muffle brand Carbonate (Z19), a stove brand Polenco (Z20) and a
hotplate brand SCP Science (Z21).
As is shown in Figure 3, a
series of verifications are carried out to ensure the quality of the results.
Weights are used to verify scales that later are used to verify the volumetric
material (Pipettes and Dispenser). Meanwhile, standard solutions are prepared
using pipettes and certified reference material to calibrate and verify an
Atomic Absorption Spectrophotometer. Temperature equipment (muffles, hotplate,
and stove) is verified by a verified thermometer. In addition, humidity and
temperature conditions are monitored using a thermohygrometer.
The samples to be analyzed are dried in
an oven at 50 °C. In the first stage of the test, high-temperature equipment is
required. The sample is roasted at 700 °C to eliminate interferences; then, the
sample is melted with a lead-based flux charge at 1000 °C. Balances are used to
prepare the flux charge and weigh the sample. In the second stage, gold is
recovered from the lead as a doré through a cupellation process at 950 °C.
Finally,
acid digestion of the doré is carried out in a digester at 60 °C, and the
resulting solution is analyzed using an atomic absorption spectrometer (Buitrón et al., 2021). By applying the Lambert-Beer law, which relates the
concentration of a substance to its absorbance, we can determine the
concentration of gold in mg/Kg of the sample. The traceability chain is presented
in Figure 3.
Figure 3 Traceability chain method of the test in the chemical
laboratory
2.3. Gray
model GM(1,1) applied to uncertainty growth in the function of time
Gray models have an acceptable
behavior when it is necessary to model data for which we have incomplete
information or to project a value in a trend whose natural causes that would
explain its behavior are unknown. The use of the laboratory equipment represents
its consumption. In consequence, there must be a loss, no matter how small, of
its precision the longer it has been used. This behavior is quantified in the
dispersion that occurs when taking successive measurements. When the equipment
is calibrated year after year, it is possible to observe its uncertainty growth
as a function of time.
The deterioration of the equipment due
to its use has imponderables that may be unknown. For this reason, it is possible
to apply GM(1,1) to the modeling of these data. However, the requirements of a
test method or a laboratory to comply with its quality standards establish a
limit tolerance. We can use this limit as a benchmark to identify the maximum
calibration interval of each piece of equipment.
Following reasoning similar to (Wang, Zhang, and Jiang, 2017), it is possible to define Equation 1:
Where U(1) is the uncertainty accumulated of
equipment, is the development coefficient, b
is the gray action, and t is time.
Using a discretization k for the calibration intervals (in
this case, years), the solution is represented in Equation 2 for a vector of uncertainties year a year
The
predicted uncertainty for period k+1
is given by Equation 3:
As
Equation 1 and the vector Y show, it
is necessary to use the amount n of
calibration uncertainty data the laboratory uses to find the constants a and b. With these results and using Equation 3, it is possible to find
the projected values and identify the period in which the uncertainty will be
outside its tolerance.
3.1. Implementation algorithm GM(1,1) given a vector of uncertainties Y
The
first step to implementing the proposed methodology is to use the following
algorithm that will allow the solving of GM(1,1) for each vector Y associated with each piece of
equipment present in the different traceability chains Figures 1 and 2:
Step 1:
Define the vector Y with its n calibration data
Step 2:
Calculates the cumulative vector of uncertainties,
Step 3:
Define the system of n-1 equations
(Equation 2).
Step 4:
Solve for a and b using the method of
least squares for n-1
equations
Step 5:
Define the tolerance limit (L)
allowed by the test method or laboratory
Step 6:
Project the uncertainties (Equation 3) until
Step 7: Find the period it is needed for, k.
In most cases, effective
data modeling is achieved through the use of algorithms, particularly when
there is a substantial amount of data available to feed the model. An
illustrative example is presented in Figure 4 and Figure 5.
3.2. Weighting of the experimental system based on its traceability chain
If the
experimental scheme for the two tests is understood as a single calibration
scheme, it is inferred that together, there must be a maximum calibration time
for the set.
The
idea of an automatic test system (ATS) composed of individual equipment has
previously been explored (Jinzhe and Jiulong, 2017a).This idea is a
solution to the exaggerated calibration times that result from the application
of different techniques for intervals of calibration.
Some
equations to determine calibration intervals have in their denominator the
difference between the corrections of two successive calibrations. If the
correction is equal, the calibration time tends to infinity, which is incorrect
from a conceptual point of view. Interpreting the calibration time of the
entire test system as a maximum calibration time for any equipment limits these
calculation overruns that can appear even in the use of GM(1,1). So that the
maximum calibration time can be calculated by Equation 4 for i individual equipment:
Figure 4 Modeling result by GM(1,1) of the electrical parameter
meter (voltmeter) in luminous intensities test in luminaires
Figure 5 Modeling result by GM(1,1) of a pipette in the gold concentration test
The
weighting factor will then be relative to each piece of equipment`s influence
on the test result, which can be visualized in the traceability chains. It is
possible to create a matrix in
which Z represents each piece of
equipment and
their relationship in
the transfer of traceability. If there is a relationship, a value of 1 is
associated; otherwise, 0. So, weighting must follow the relationship in
Equation 5 in j relations (Jinzhe and Jiulong, 2017b; Wang, Zhang, and Jiang, 2017).
Results
are shown in Table 1. Once the weighting is applied, we get tmax=4 years for the
Physical-Photometric laboratory and tmax=10
years for the Chemical laboratory. Then, the calibration plan must consider the
time delivered by the GM(1,1) algorithm for each piece of equipment if it is
less than tmax and tmax if it is greater.
Changes in calibration plans represent greater efficiency (Velásquez et al.,
2024) in terms of financial resources (Woodhead and Berawi, 2020).
The Physical-Photometric and Chemical laboratories pay around 4600 USD and 1000
USD annually, respectively, in a year-to-year calibration plan. The implementation
of this methodology has effectively minimized the technical risks associated
with the shift calculation, particularly the occurrence of exaggeratedly high
values in subsequent calibrations. Additionally, it resulted in savings of 11%
and 54% in each case for the following year.
The projection of the
behavior of each piece of equipment is obtained by working together as a single
experimental scheme in the test, weighing the importance of each one in the
traceability chain. This proves to be a critical factor, as obtaining a maximum
timeframe within these weight limits not only mitigates the duration of
calibration but also enables the formulation of an optimized calibration plan.
The methodology tested with chemical and physical laboratories found that the
technique can be applied regardless of its particular characteristics.
Table 1 matrix Physical-Photometric laboratory and
matrix Chemical laboratory
The ISO/IEC 17025
standard requires the calibration of systems and equipment. Calibration
intervals must be flexible, but the options for calculating them can generate
some technical complications. The main problem is a long calibration interval
in which the technical concept of "calibration" loses meaning. The
gray model GM(1,1) applied to the uncertainty of calibration of historical data
allows for the projection of the uncertainty of equipment for the following
period. The tolerance defined by the laboratory or the test/calibration method
is a limit with which we can compare the projected values and satisfactorily
estimate the next calibration period. The GM(1,1) technique has considerable
technical efficiency and saves the economic resources allocated to calibration
in the year-to-year plan. Two different tests were studied with this
methodology. The results are applicable in the physical or chemical nature of
laboratories. There was a reduction of 11% and 54% in financial resources,
respectively, while maintaining technical confidence. However, if this
methodology is applied, it is essential to have a verification plan to maintain
the security of its technical competence with additional measures. Based on the
results obtained, interesting future work is to model a risk analysis
associated with the differential model used.
The authors thank TRANSELECTRIC
E.P. for its facilities for the use of the IIGE lighting laboratory and the
lighting laboratory and chemical laboratory of IIGE for opening their
information on measurement equipment.
Brusil, C., Arcos, H., Espin, F.,
Velasquez, C., 2020. Analysis
of Harmonic Distortion of LED Luminaires Connected to Utility Grid. In: 2020 IEEE ANDESCON, pp. 1–6
Brusil, C., Espín, F., Velásquez,
C., 2021. Effect of Temperature in
Electrical Magnitudes of LED and HPS Luminaires. International Journal of
Electrical and Computer Engineering Systems, Volume 12(4), pp. 225–234
Buitrón, D.O., Barona D.D., Iturra F.M., Leon, J.F.,
2021. Validación
del Método Para la Determinación de Oro por Ensayo al Fuego Combinado con
Espectrometría de Absorción Atómica en Muestras Geológicas Mineras Metalúrgicas
(Validation of The Gold Determination Method by Fire Assaycombined with Atomic
Absorption Spectrometry in Geological, Mine And Metallurgical Samples). InfoANALÍTICA, Volume 9(1), 2021, pp. 119–136
Butdee, S., Khanawapee, U., 2021. Quality Prediction
Modeling of a Preform Fastener Process using Fuzzy Logic and DEFORM Simulation.
International Journal of Technology, Volume 12(1), pp. 33–42
Commission Internationale de L’Eclairage (CIE),
2009. The Photometry and
Goniophotometry of Luminaires - Supplement 1: Luminaires for Emergency
Lighting. Central Bureau of the CIE, CIE
121 -SP1, Vienna, Austria
Commission Internationale de L’Eclairage (CIE), 2015. Test Method for LED Lamps, LED
Luminaires and LED Modules. CIE S025, Vienna, Austria
Deepradit, S., Ongkunaruk, P., Pisuchpen, R., 2020.
Tactical Procurement Planning under Uncertainty in Aromatic Coconut
Manufacturing. International Journal of Technology, Volume 11(4), pp.
698–709
Delker, C.J., Auden, E.C.,
Solomon, O.M., 2020. Calculating Interval Uncertainties for Calibration
Standards That Drift with Time. The Journal of Measurement Science,
Volume 12(4), pp. 9–20
EL-Hadad, R., Tan, Y.-F., Tan, W.-N., 2022. Anomaly
Prediction in Electricity Consumption Using a Combination of Machine Learning
Techniques. International Journal of Technology, Volume 13(6), pp.
1317–1325
Ellison, S.L.R., 2014. Implementing Measurement
Uncertainty for Analytical Chemistry: the Eurachem Guide for Measurement
Uncertainty. Metrologia, Volume 51(4), p. S199
Gaber, S.E., 2021. Adjusting External Calibration
Intervals for Auxiliary Devices in Testing Laboratories According to
Intermediate Checks Results. Water Science, Volume 35(1), pp. 82–88
González, A.G., Herrador, M.Á.,
Asuero, A.G., Martín, J., 2018. A
Practical Way to ISO/GUM Measurement Uncertainty for Analytical Assays
Including In-House Validation Data. In: Quality Control in Laboratory, pp.
109–130
Illuminating Engineering Society, 2019. ANSI/IES LM-79-19 - Approved Method: Optical and
Electrical Measurements of Solid-State Lighting Products. Illuminating
Engineering Society, New York, USA
International Organization for Standardization (ISO), 2017. ISO/IEC 17025:2017 General Requirements for The
Competence of Testing and Calibration Laboratories. International Organization
for Standardization
Jinzhe, X., Jiulong, X., 2017a. Calibration Interval
Optimization and Calibration Conclusion Risk Analysis on Automatic Test System.
In: ICEMI 2017 - Proceedings of IEEE 13th International
Conference on Electronic Measurement and Instruments, pp. 236–241
Jinzhe, X., Jiulong, X., 2017b. Calibration Interval
Optimization and Calibration Conclusion Risk Analysis on Automatic Test System.
In: 13th IEEE International Conference on Electronic Measurement
& Instruments (ICEMI), pp. 236–241
Joint Committee for Guides in Metrology, 2008. Évaluation
Des Données De Mesure-Guide Pour L’expression De L’incertitude De Mesure (Evaluation
of Measurement Data-Guide to The Expression of Uncertainty in Measurement).
Joint Committee for Guides in Metrology
Juiña, D., Silva, B., Velásquez,
C., 2024. Análisis
De Riesgo De La Declaración De Conformidad De La Potencia De Luminarias a Un
Nivel Determinado De Confianza (Risk Analysis of the Declaration of
Conformity of Luminaire Power at a Given Level of Confidence). Killkana Técnica, Volume 7(1), pp. 46–60
Kopke,
V., Mourão, S., Brito, M., 2024. Determination of the Calibration Interval of
Measuring Instruments: Which Method Should I Use? IEEE Instrumentation &
Measurement Magazine, Volume
27(2), pp. 59–62
Legal International Organization of Metrology, 2007. ILAC-G24-OIML
D 10 Guidelines for The Determination of Calibration Intervals of Measuring
Instruments. Legal International Organization of Metrology
Lin, K.-H., Liu, B.-D., 2005. A Gray System Modeling Approach to the Prediction of
Calibration Intervals. IEEE Transactions on Instrumentation and Measurement,
Volume 54(1), pp. 297–304
Muscas, C., Peretto, L.,
Sasdelli, R., Briani, A., 2001. An
Automatic Test Equipment for the Calibration of Voltage Transducers. IEEE
Transactions on Instrumentation and Measurement, Volume 50(6), pp.
1638–1643
Nugraha, E., Sari, R.M.,
Sutarman, Yunan, A., Kurniawan, A., 2022. The Effect of Information Technology,
Competence, and Commitment to Service Quality and Implication on Customer
Satisfaction. International Journal of Technology, Volume 13(4), pp. 827–836
Pashnina, N., 2020. Corrigendum to “Determination of
Optimal Calibration Intervals by Balancing Financial Exposure Against
Measurement Costs”. Flow Measurement and Instrumentation, Volume 60C,
pp. 115–123
Silva, M.D.G.D., Rodrigues, A.B., 2013. Reliability Data
Calibration Based on Load Point Interruption Indices Using Nonlinear and
Quadratic Optimization. In: 2013 IEEE Grenoble Conference, pp. 1–6
Taymanov, R., Teteruk, R., Sapozhnikova, K.,
Medvedevskikh, S., 2023. Metrological Reliability of Measuring Instruments and
the Possibilities for its Improvement. In: XXXIII International
Scientific Symposium Metrology and Metrology Assurance (MMA), Sozopol,
Bulgaria, pp. 1–5
Toteva, P., Slavov,
S., Vasileva, D., 2017. Comparison
of the Methods for Determination of Calibration and Verification Intervals of
Measuring Devices. In: MATEC Web of Conferences, Volume 94, p. 04012
Velásquez, C., Castro, M.Á., Rodríguez, F., 2021b. Analysis
of a Reinterpretation of Gray Models Applied to Measuring Laboratory Equipment
Uncertainties. In: Modelling for Engineering & Human Behaviour,
Torregrosa, J.R., Cortés, J.C., Hervás, J.A., Vidal-Ferrándiz, A.,
López-Navarro, E., (ed.), Universitat Politécnica de Valencia, pp. 252–255
Velásquez, C., Castro, M.A.,
Rodríguez, F., Espín, F., Falconi, N., 2021a. Optimization of the Calibration Interval of a Luminous
Flux Measurement System in HID and SSL Lamps Using a Gray Model Approximation. In:
2021 IEEE Fifth Ecuador Technical Chapters Meeting (ETCM), pp. 1–7
Velásquez, C., Espín, F., Castro, M.Á., Rodríguez, F.,
2024. Energy Efficiency in Public Lighting Systems Friendly to the Environment
and Protected Areas. Sustainability, Volume 16(12), p. 5113
Velásquez, C., Espín, F.,
Rodríguez, F., Castro, M.Á., 2023. Heat
Transfer Modeling in Road Lighting LED Luminaire. In: AIP Conference
Proceedings, Volume 2872(1), p. 020013
Velásquez, C., Juiña, D., Iturra, F., Silva, B., Barona,
D., 2024. Methodology for Declaration of Conformity Under ISO/IEC 17025
Associating Confidence Levels and Risk Analysis. In: Innovation and Research – Smart
Technologies & Systems, Vizuete, M.Z., Botto-Tobar, M., Casillas, S.,
Gonzalez, C., Sánchez, C., Gomes, G., Durakovic, B., (ed.), pp. 30–42
Wang, J., Zhang, Q., Jiang, W., 2017. Optimization of
Calibration Intervals for Automatic Test Equipment. Measurement: Journal of
the International Measurement Confederation, Volume 103, pp. 87–92
Wibawa, A., Ichsani, D., Yuniarto, M.N., 2021. Holistic
Operation & Maintenance Excellence (HOME): Integrating Financial &
Engineering Analysis to Determine Optimum O&M Strategies for a Power Plant
during its Lifetime. International Journal of Technology, Volume 12(4),
pp. 813–828
Woodhead, R., Berawi, M.A. 2020. Value Creation and the Pursuit of Multi Factor Productivity Improvement. International Journal of Technology, Volume 11(1), pp. 111–122
Zeng, B., Ma, X., Shi, J., 2020. Modeling Method of the Grey GM(1,1) Model with Interval Grey Action Quantity and Its Application. Complexity, Volume 2020, pp. 6514236
