Experimental Study of Linear Profile Modification in Spur Gear Leg
Published at : 17 May 2024
Volume : IJtech
Vol 15, No 3 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i3.5851
Pramono, A.S., Wikarta, A., Mu’iz, F., 2024. Experimental Study of Linear Profile Modification in Spur Gear Leg. International Journal of Technology. Volume 15(3), pp. 665-676
| Agus Sigit Pramono | Department of Mechanical Engineering, Faculty of Industrial Technology and Systems Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Keputih-Sukolilo Surabaya 60111, Indonesia |
| Alief Wikarta | Department of Mechanical Engineering, Faculty of Industrial Technology and Systems Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Keputih-Sukolilo Surabaya 60111, Indonesia |
| Fakhul Mu’iz | Department of Mechanical Engineering, Faculty of Industrial Technology and Systems Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Keputih-Sukolilo Surabaya 60111, Indonesia |
Gears with the involute profile are assumed to be rigid and
good at producing mating gear. They are also deformable and deflectable,
indicating additional space is required to avoid interference from the
unpredictable shaft, misalignment, and dynamic factors. In addition, load and
rotational speed cause frequent mild to severe interference leading to a
significant reduction in its lifespan. This study conducted an experimental
comparison between standard and modification involute gear profiles in a ratio
of 1:2 to reduce interference. It was carried out using 18 pinion teeth with a
72 mm base diameter at three and four levels of torque load and speed. The load
was also mounted a strain gauge on pinion gears to conduct strain measurement
on the gear leg. Finally, it was applied using a mechanical brake measured by a
dynamic torque meter. The experimental test obtained microstrain when the
modified spur gear contacted for 3.04 – 6.67 milliseconds depending on the
rotation speed and torque load. Modification of the linear involute profile
significantly reduced the tooth leg strain at the rate of 5.6% to 13.99%.
Meanwhile, the maximum microstrain reduction of 13.99% occurred at a speed of
1100 rpm and a torque load of 65%.
Interference; Involute profile; Modification profile; Spur gear; Strain reduction
Modern-day mechanical gears are
widely used in transmission systems to transmit torque included in the wave
energy converter (Ariefianto,
Hadiwidodo, and Rahmawati, 2022). Despite
manufacturing new transmission systems with magnetic gears, no physical contact
between materials has been identified (Rahman,
Hassan, and Ihsan, 2022; Niguchi, Hirata and Zaini, 2013). (Li
and Bird, 2018) stated
that these various benefits of mechanical gears prevent the need for
lubrication, high durability, and a high-speed-reduction ratio. Its main
shortcoming includes lower torque density. Therefore, continuous efforts are
carried out to extend the service life and reduce mechanical gear vibrations.
When a backlash is overly narrow, it causes overheating, overload, noise, and
jamming, while a loose one leads to a significant impact load and excessive
vibrations (Dyaneshwar
and Mangrulkar, 2016).
The amount of backlash can be determined by considering various factors. The first factor is based on the module range or diametral pitch, while the second factor involves evaluating the diametral pitch and the centre of the distance axis. A third factor utilizes the second parameter of diametral pitch and line velocity. However, it is often difficult to determine the exact amount of backlash required due to manufacturing imperfections. (Karba et al., 2019).
Planned backlash aims to increase
the distance between the shafts or cut the side of the gear. The study by (Sharma,
Moorthy and Kumar, 2015) used
the finite element method to investigate strain reduction in the spur gear leg.
Unplanned backlash with unpredictable magnitude cause problems involving
various parameters, such as tooth and shaft deflections, load, rotational
speed, bearing clearance, temperature, and lubrication. The concept of a second
factor caused by material stiffness and contact stress was further developed to
address contact stress between non-metal and non-metal (Rahman,
Shoukaku, and Iwai, 2021).
Meanwhile,
(Eritenel
et al., 2003) conducted
a numerical study using the finite element method. The study found that the
fillet radius caused bending deflection, which influenced the base stiffness as
defined by (Joshi
and Karma, 2011),
and this in turn affected the magnitude of the backlash.
(Guo,
Keller, and LaCava, 2012) conducted
a study on the effect of bearing clearance distance on planetary stress. The
study found that increased bearing clearance leads to a higher non-torque
workload. Preliminary studies have been conducted using numerical simulations
and approximation equations to determine the minimum gap width in the
elastohydrodynamic lubrication (EHL) channel (Dowson
and Higginson, 2014; Lubrecht, Venner and Colin, 2009). (Li
and Kahraman, 2011) selected
a similar approach involving the pre-calculation of dynamic tooth strength.
Meanwhile, (Jeon
et al., 2011) designed
the last factor using an inaccurate profile of 0.015 to 0.033 EDM.
This study addressed the
requirement for adequate backlash by implementing a critical profile
modification. Prior research has explored the transformation of the tooth
profile using the modeling and dynamic simulation (Liang,
Zuo, and Feng, 2018),
artificial neural networks (Devendiran
and Manivannan, 2015b),
and genetic algorithms (Devendiran
and Manivannan, 2015a).
One of the critical problems in the industry is determining what to do,
assuming the service life of the gear is shorter than expected. According to
studies, the easiest and most expensive solution is replacing the gear or
modifying its tooth through lead modification processes in the axial direction
to reduce the effect of load concentration due to misalignment. Profile
modification targets tooth deflection due to mechanical loads. Therefore, the
available backlash does not provide free space, which causes low to high
interferences, leading to jamming.
The tooth profile modification on
the gears occurs in the dedendum and addendum areas. Addendum modifications,
also known as profile tips or relief modifications, are more common than
dedendum due to their inability to reduce bending strength. The amount (?) and
length of profile modification (Ln)
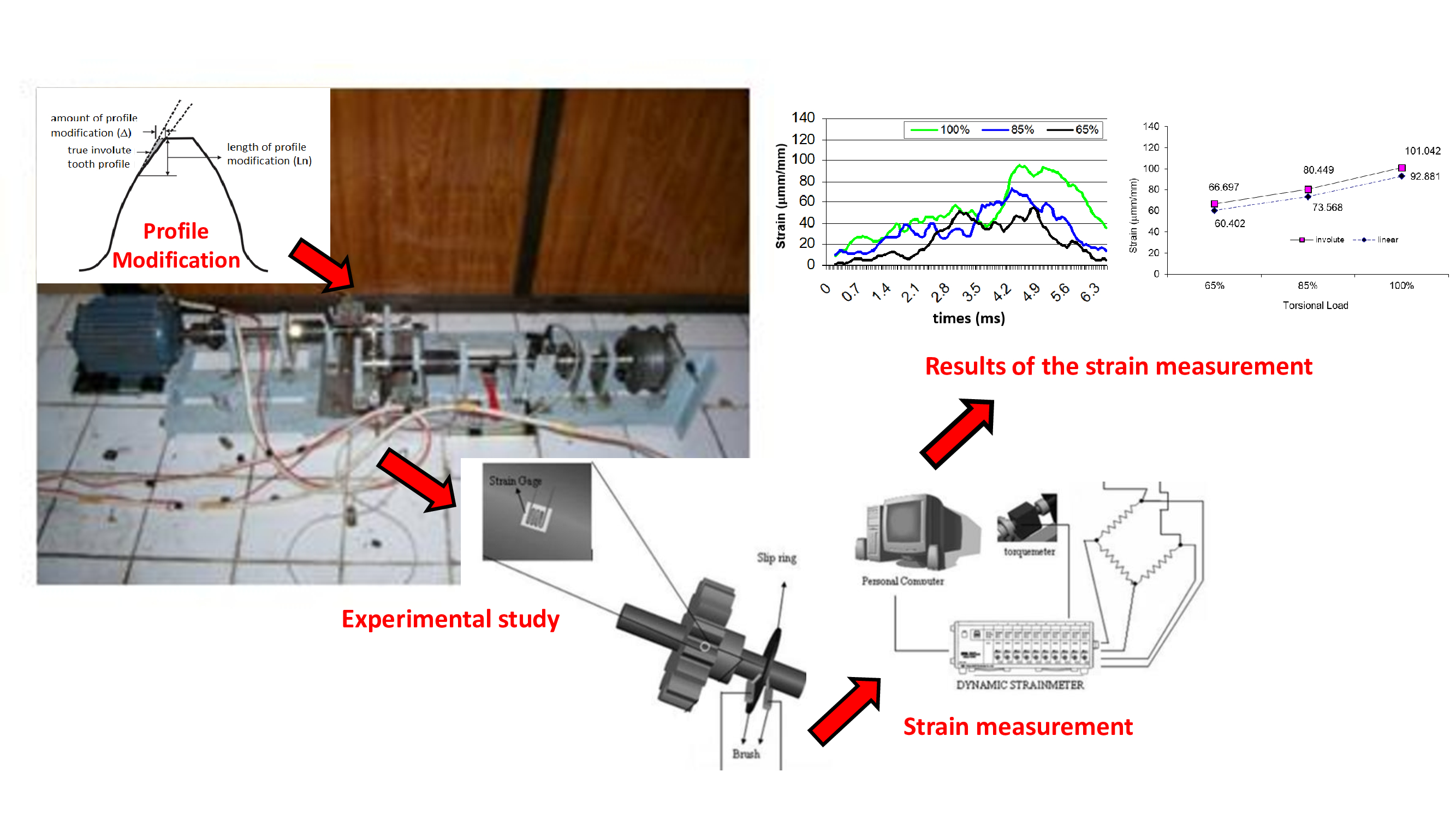
are the parameters used to modify the profile tip, as presented in Figure 1.
Amount profile modification is an important parameter determined by the actual
operating conditions. It is estimated by determining the mechanical and thermal
loads deflection and the error profile of the manufacturing process.
This study was conducted using the tooth flexural deflection and contact deformation with a linear tip relief profile (Markovi? and Vrcan, 2016; Buljanovic and Obsieger, 2009). Modifications to the linear tooth profile led to a lower dynamic response compared to the unmodified tooth profile. Furthermore, the modifications involved different gear types, including spur (Ghosh and Chakraborty, 2016; Li et al., 2016), helical (Wu, Wang and Han, 2012), and planetary gears (Bahk and Parker, 2013) studied through finite element modeling and simulation.
Figure
1 Profile of modification parameters
Experimental methods were employed to measure
the stress-strain in the root tooth, including the use of strain gauges (Lisle, Shaw, and
Frazer, 2019) and
photoelasticity (Raptis and
Savaidis, 2018).
The experimental fatigue method was conducted by calculating the cycle and
administering the load in stages (Concli, 2021; Liang,
Zuo, and Feng, 2018).
It is more challenging to take dynamic robot tooth measurements in real-time
because it requires data logger equipment capable of speedily recording dynamic
data and writing the entanglement problem. Most dynamic photoelasticity
measurement methods use a stroboscope to produce quasi-static or momentary
photos (Patil, Patil, and
Nulke, 2018).
Few related studies existed on using a high-speed camera to record real-time
data using transient dynamic photoelasticity measurements. In the symmetric gear tip relief profile, it can not only
reduce the bending stress but also reduce the contact stress (Molnár, Csoban, and Zwierczyk, 2021).
Another way to increase bending strength is to use
asymmetric gears formed from two involute profiles with
different contact angles on the drive and coast sides. Several studies have
been conducted on these gears. For instance, (Pramono and Rizal,
2021) researched the influence of the asymmetric factor to reduce
bending stress, using the contact-angle cosine ratio of the drive and coast
sides as the asymmetric factor, representing the symmetric spur gear. The
greater the asymmetric factor, the higher the contact angle difference and
decreased bending stress. Furthermore, (Mallesh et al.,
2009) studied the effect of profile shift on the bending
stress of asymmetric gears with x values of 0, 0.1, 0.2, 0.3, 0.4, and 0.5. The
results showed that the larger the profile shift, the smaller the bending
stress, applicable to different asymmetric values with contact angles of 20o
to 30o. (Mallesh and VG,
2020) also investigated modeling using the
asymmetric factor and profile shift. The increase in pressure angle on the
drive side leads to a decrease in contact ratio and tooth thickness on the
addendum circle and a rise in pressure angle. The tooth thickness on the
addendum circle decreases for gears with increased profile shifts as the
pressure angle on the drive side rises. Consequently, the bending stress at the
critical section reduces significantly.
(Mo et al.,
2022) compared the analytically obtained
meshing stiffness increased with a rise in asymmetric factors. In addition, the
modification of teeth allows for a smoother transition between single and
double ones.
Besides reducing bending stresses, asymmetric
gears with tip relief can also lead to a decline in contact stresses, as (Karpat and
Ekwaro-Osire, 2008) using Archard's analytical equation. As the amount of tip relief
increases, the wear depth, particularly at the beginning and end of the mesh,
decreases. Similarly, as the number of wear cycles increases, the effect of the
tip relief modi?cation on wear depths decreases slightly.
(Y?lmaz, Dogan, and
Karpat, 2017) proposed the
asymmetric trochoid profile to
decrease maximum bending stress and move the upper critical point. It is
evaluated that effect of rim thickness on bending stress is more significant
for those less than 1.3×module because of higher rim deformations.
Although asymmetric gear has the
advantage of increasing bending and contact strength, it also has the
disadvantage of rotating in only one direction, indicating it cannot be used
for two-way transmission. When the drive side is worn, it must be replaced,
unlike the symmetric gear, which can be reversed. Therefore, further study is
needed to investigate the performance difference between symmetric and
asymmetric gears.
This
experimental study involved a linear comparison between the standard and
modified involute gear profile at a ratio of 1: 2, where the number of pinion
teeth and diameter are 18 and 72 mm.
Strain measurements were taken using a strain gauge mounted on one
pinion tooth, with slip rings used to avoid entangling the cable during
rotation. Load torque was measured using a mechanical brake.
The various experimental stages include making standard tooth profiles
and modifications, designing, manufacturing, and setting up test equipment or
benches. The last experiment tested both the standard and the modified profile
by following procedures, as shown in Figure 2.
Figure 2
Flowchart of experiment procedures for spur gear with profile modification
2.1 Determination of the Number of Pinion Teeth
Involute
gears can be readily generated by rack-type cutters, such as hob. Gear
generation can also be also accomplished with gear-type cutters using a shaper
or planer machine. In the production of standard straight gears, a
small number of teeth can lead to undercutting at the dedendum. The undercut
not only weakens the tooth with a wasp-like waist but also removes some of the
useful involute adjacent to the base circle. To determine the minimum number of
teeth required to avoid undercutting, one can refer to Equation (1) (Michalec et al., 2009).
where :
However, if a smaller number of teeth is desired without undercutting,
standard spur gears may require modifications such as profile shifting, which
is described by Equation (2) (Michalec et al., 2009).
where :
In this study, standard spur
gears without undercutting were used, following Equation (1), and with a
contact angle of 20 degrees, the number of pinion teeth was determined to be
18.
2.2. Profile
Modification
Straight
gears are made of a standard involute surface gear profile and a linear
modified involute, which start at distances of 1 1.8 mm and 1.6 mm,
respectively. The cut at the tip of the tooth is 0.104 mm and 0.091 for the
pinion and gear, respectively, as shown in Figure 3.
Figure 3 Profile of
modification (a) pinion and (b) gear
2.3.
Design and Prototype of Test Bench
A
test device was designed to measure the stress on the tooth root, as shown in Figure
4. The device is powered by a 1500 rpm motor with 1.5 horsepower. A Dynamic
Torquemeter with a maximum torque of 160 Nm is mounted on the motor shaft and
connected to the pinion spur gear shaft. A slip ring is installed near the
pinion spur gear with a strain gauge attached to one of the root teeth. The
slip ring is further connected to a series of bridge stones and a dynamic data
logger linked to a PC. Once the pinion spur gear is
paired with the driven spur gear, slip rings are installed. Finally, a brake
system is installed as a load at the drive shaft's end.
2.4. Determination
of Time for One Contact Gear
Due to the varying rotating speeds, it
is necessary to calculate the time of one contact gear for each rate. It takes
1/8.33 = 0.12 seconds for the motor shaft speed of 500 rpm or 8.33 rps to
completely rotate for 18 teeth. Therefore, one gear contact takes 0.12/18 = 0.0066
seconds or 6,67 milliseconds. The same calculation is carried out for other
speeds, and the results are presented in Table 1.
Table 1 Contact duration on one teeth pair
|
Angular speed |
Contact duration of one teeth pair (ms) | |
|
rpm |
rps | |
|
500 |
8.33 |
6.67 |
|
700 |
11.66 |
4.78 |
|
900 |
15.00 |
3.72 |
|
1100 |
18.33 |
3.04 |
The stain gage mounted on one
of the root teeth is a uniaxial strain gage that follows the bending direction
with microstrain units. Following Hook's law, the bending stress in the elastic
zone can be obtained, where the strain is proportional to the stress with a
constant of proportionality.
The measurement resulting from a strain gauge is shown on a
graph where the abscissa and the ordinate axis represent time and strain,
respectively. Figure 5 shows the pinion with a rotation of 500 rpm. The maximum
strain decreases due to linear modification for all load levels, which reduces
the level of dynamic interference.
Figure 5
The results of the strain measurement on one teeth pair in contact at 500 rpm:
(a) pinion involute, (b) pinion linear
The
data involved maximum strain in facilitating comparison and further analysis. Figure
6 shows that the increase in torsional load raises the strain in the gear leg
for all speeds in standards and modified involute profiles. This is in line
with a theory that increasing the load will enlarge strain on the tooth foot
and raise the tooth deflection, thereby causing interference.
In Figure
7, an increase in rotation at a constant load led to a rise in the strain and
all load levels in accordance with the characteristics of an AC motor using a
speed controller with an inverter. Furthermore, an increase in rotation led to
a rise in the motor shaft and a slight rotation of the AC.
At 500
rpm rotation and 65% load, the profile modification reduced the strain by
9.44%, 8.55%, and 8.08% for 65%, 85%, and 100% loads, respectively. Meanwhile,
at 1100 rpm rotation and 65% load, a maximum strain reduction of 13.99% was
obtained, while at 85% load, it decreased by 11.48%. However, at 100% load, the
strain decreased again to 9.41%, indicating that interference starts with
increased tooth deflection.
Figure 6 Comparison of strain as a function of load at (a) 500 rpm, (b) 700 rpm, (c) 900 rpm, and (d) 1100 rpm
An
evident increase in load leads to a decrease in strain reduction. This is
because the increase in load raises the deflection, thereby increasing the
level of interference. An increase in load raises interference levels in all
rotations by 500, 700, 900, and 1100 rpm, causing strain to decrease.
Other
studies mostly came from simulations since experiments are rarely conducted.
Even though experiments were performed, they did not carry out variations in
loading and rotation. Therefore, the effectiveness of modifying the involute
spur gear in various conditions experienced by the gear pair cannot be
determined.
This study confirms the
findings of (Li
et al., 2016) that modifying the involute
spur gear can reduce impact and noise at the contact point by decreasing the
strain value on the modified pinion gear. This reduction in strain helps to
achieve an appropriate amount of backlash to prevent overheating, noise,
impact, and excessive vibration.
This
study proves that the reduction in strain value can occur in various loading
and rotation conditions. Preliminary studies on tooth profile modification (Dai,
Cooley, and Parker, 2016; Ghosh and Chakraborty, 2016; Bahk and Parker, 2013;
Wu, Wang and Han, 2012) only focused on specific
loading conditions. Therefore, the impact of profile modification is unknown
for various conditions in spur gear pairs.
This dynamic experimental study also has advantages compared
to other studies focused on maximum conditions. The contact between the spur
gears for 3 - 6 ms can be well observed using the measuring instrument.
Furthermore, the measurement results in microstrain can be graphed as shown in
Figure 8. This cannot be found in the photoelasticity experimental method (Raptis and
Savaidis, 2018).
Figure 7 Maximum strain ratio as a
function of speed at (a) 65%, (b) 85%, and (c) 100% load
Figure 8 Reduction of strain between standard and
modified linear profile
In conclusion, several experimental studies determined
the effect of tooth profile modification on standard and linearly modified gear
profiles by comparing and analyzing the results. The reduction in micro-strain
was observed for a duration of 3.04 – 6.67 milliseconds, depending on the
rotation speed and torque load. Modifying the linear involute profile
significantly reduced tooth leg strain, ranging from 5.6% to 13.99%, depending
on the load and speed. The maximum reduction in micro-strain of 13.99% was
achieved at a rate of 1100 rpm and a torque load of 65%, increasing tooth
strength against bending loads. It is important to note that reducing tooth leg
strain is crucial for ensuring the longevity and durability of gears in various
real-world scenarios. Further studies could explore the impact of tooth profile
modification on other gear types and sizes and investigate the effect of
different parameters, such as lubrication, on gear performance. Overall, the
findings of this study have a valuable contribution to understanding modified
gear profiles and their impact on gear strength and durability.
Ariefianto, R.M., Hadiwidodo, Y.S., Rahmawati, S.,
2022. Experimental Study of a Wave Energy Converter Using a Unidirectional
Cascaded Gear System in a Short-Wave Period. International Journal of
Technology, Volume 13(2), pp. 321–331
Bahk,
C.-J., Parker, R.G., 2013. Analytical Investigation of Tooth Profile
Modification Effects on Planetary Gear Dynamics. Mechanism and Machine
Theory, Volume 70, pp. 298–319
Buljanovic,
K., Obsieger, B., 2009. Influence of Tip Relief Profile Modification of Spur
Involute Gears on Stresses. International Journal Advanced Engineering,
3, pp. 149–158
Concli,
F., 2021. Tooth Root Bending Strength of Gears: Dimensional Effect for Small
Gears Having a Module Below 5 mm. Applied Sciences, Volume 11(5), p.
2416
Dai,
X., Cooley, C.G., Parker, R.G., 2016. Dynamic Tooth Root Strains and
Experimental Correlations in Spur Gear Pairs. Mechanism and Machine Theory,
Volume 101, pp. 60–74
Devendiran,
S., Manivannan, K., 2015a. An Intelligent Gear Fault Diagnosis Model Based on
EMD and Evolutionary Algorithms. International Journal of Mechanical &
Mechatronics Engineering IJMME-IJENS, Volume 15(1), p. 10
Devendiran, S., Manivannan, K., 2015b. Vibration
Signal Based Multi-fault Diagnosis of Gears using Roughset Integrated PCA and
Neural Networks. International Journal of Mechanical & Mechatronics
Engineering IJMME-IJENS, Volume 15(01), p. 11
Dowson,
D., Higginson, G.R., 2014. Elasto-Hydrodynamic Lubrication: International
Series on Materials Science and Technology. Elsevier
Dyaneshwar,
S., Mangrulkar, K.S., 2016. Effect Of Backlash on Bending Stresses in Spur
Gears. International Journal of Scientific Development and Research,
Volume 7, pp. 349–354
Eritenel,
T., Houser, D.R., Vijayakar, S.M., Casella, J.M., 2003. Effect of Tooth
Deflection and Corner Contact on Backside Separation (Backlash) of Gear Pairs. In:
9th International Power Transmission and Gearing Conference, Parts A
and B. ASME 2003 International Design Engineering Technical Conferences and
Computers and Information in Engineering Conference. Volume 4, pp. 103–110
Ghosh,
S.S., Chakraborty, G., 2016. On Optimal Tooth Profile Modification for
Reduction Of Vibration And Noise In Spur Gear Pairs. Mechanism and Machine
Theory, Volume 105, pp. 145–163
Guo,
Y., Keller, J., LaCava, W., 2012. Combined Effects of Gravity, Bending Moment,
Bearing Clearance, and Input Torque on Wind Turbine Planetary Gear Load
Sharing: Preprint. In: American Gear Manufacturers Association;
(AGMA) Fall Technical Meeting, Dearborn, Michigan: National Renewable
Energy Lab. (NREL), Golden, CO (United States). Available online at:
https://www.osti.gov/biblio/1050766, Accessed on September 3, 2020
Jeon,
E.C., Lee, S.Y., Song, H.B., Chun, J.D., Kim, S.Y., 2011. Study for the
Verification of the Tooth Profile Accuracy of the Automatic Gear Design
Program. Global Journal of Technology and Optimization, Volume 2(1), pp.
97–103
Joshi, A., Karma, V.K., 2011. Effect on
Strength of Involute Spur Gear by Changing the Fillet Radius Using FEA. International
Journal Of Scientific & Engineering Research, Volume 2(9), p. 5.
Karba,
B., Y?ld?r?m, N., Erdo?an, F., Vardar, M., 2019. A Study on Prediction &
Validation Of Meshing Gear Pair Backlash Under Various Manufacturing And
Assembly Errors. In: MATEC Web of Conferences. Volume 287, p.
07001
Karpat, F., Ekwaro-Osire, S., 2008. Influence
Of Tip Relief Modification On The Wear Of Spur Gears With Asymmetric Teeth. Tribology
Transactions, Volume 51(5), pp. 581–588
Li,
K., Bird, J.Z., 2018. A Review Of The Volumetric Torque Density Of Rotary
Magnetic Gear Designs. In: 2018 XIII International Conference on
Electrical Machines (ICEM). IEEE, pp. 2016–2022
Li,
S., Kahraman, A., 2011. Influence of Dynamic Behaviour on Elastohydrodynamic
Lubrication of Spur Gears. In: Proceedings of the Institution of
Mechanical Engineers, Part J: Journal of Engineering Tribology, Volume 225(8),
pp. 740–753
Li,
X.Y., Wang, N.N., Lv, Y.G., Zeng, Q.L., Hidenori, K., 2016. Tooth Profile
Modification and Simulation Analysis of Involute Spur Gear. International
Journal of Simulation Modelling, Volume 15(4), pp. 649–662
Liang,
X., Zuo, M.J., Feng, Z., 2018. Dynamic Modeling of Gearbox Faults: A Review. Mechanical
Systems and Signal Processing, Volume 98, pp. 852–876
Lisle,
T.J., Shaw, B.A. Frazer, R.C., 2019. Internal Spur Gear Root Bending Stress: A
Comparison of ISO 6336: 1996, ISO 6336: 2006, VDI 2737: 2005, AGMA, ANSYS
Finite Element Analysis and Strain Gauge Techniques. In: Proceedings of
the Institution of Mechanical Engineers, Part C: Journal of Mechanical
Engineering Science, Volume 233(5), pp. 1713–1720
Lubrecht,
A.A., Venner, C.H., Colin, F., 2009. Film Thickness Calculation in
Elasto-Hydrodynamic Lubricated Line and Elliptical Contacts: The Dowson,
Higginson, Hamrock Contribution. In: Proceedings of the Institution of
Mechanical Engineers. Part J: Journal of Engineering Tribology, Volume
223(3), pp. 511–515
Mallesh,
G., Math, V.B., Ashwij, P.S.D.R., Shanbhag, R., 2009. Effect of Tooth Profile
Modification in Asymmetric Spur Gear Tooth Bending Stress by Finite Element
Analysis. In: 14th National Conference on Machines and Mechanisms
(NaCoMM09), NIT, Durgapur, India, pp. 17–18
Mallesh,
G., VG, P.K., 2020. Optimization of Asymmetric Spur Gear Tooth. International
Research Journal of Engineering and Technology (IRJET), Volume 7, pp.
363–370
Markovi?,
K., Vrcan, Ž., 2016. Influence of Tip Relief Profile Modification on Involute
Spur Gear Stress. Transactions of FAMENA, Volume 40(2), pp. 59–70
Michalec,
G., Buchsbaum, F., Tanaka, H., Shuett, L., Chiaramonte, J., Sondej, S.,
Hasranah, M., Quinteros, L.C., Epstein, M., 2009. Elements of Metric Gear
Technology. Stock Drive Products & Sterling Instrument. Available
online at: https://gearkade.
com/wpcontent/uploads/2019/08/Elements-of-Metric-Gear-Technology.Pdf, Accessed
on February 11, 2022
Mo,
S., Li, Y., Luo, B., Wang, L., Bao, H., Cen, G., Huang, Y., 2022. Research on
The Meshing Characteristics of Asymmetric Gears Considering The Tooth Profile
Deviation’, Mechanism and Machine Theory, Volume 175, p. 104926
Molnár,
J., Csoban, A., Zwierczyk, P.T., 2021. Analysis of Tip Relief Profiles for
Involute Spur Gears. ECMS, Volume 35(1), pp. 147–151
Niguchi, N., Hirata, K., Zaini, A., 2013. Electromagnetic
Vibration Analysis and Measurement of a Magnetic Gear. IEEJ Journal of
Industry Applications, Volume 2(6), pp. 261–268
Patil,
P.J., Patil, A.A., Nulke, S.S., 2018. Dynamic Analysis of Helical Gear To
Evaluate Bending Stress At Root Of Tooth Using Photoelastic Coating And Finite
Element Method. International Journal of Advance Research in Science and
Engineering, Volume 7(3), pp. 133–147
Pramono,
A.S., Rizal, M.Z., 2021. Influence Of Asymmetric Factor on Spur Gears To
Dynamic Bending Stress. In IOP Conference Series: Materials Science and
Engineering, Volume 1034(1), p. 012010
Rahman, A., Hassan, N., Ihsan, S.I., 2022. Fuzzy
Logic Controlled Two Speed Electromagnetic Gearbox for Electric Vehicle. International
Journal of Technology, Volume 13(2), pp. 297–309
Rahman,
J., Shoukaku, Y., Iwai, T., 2021. An Experimental Study of the Effect of Load
and Moving Speed on Free Rotating Rubber Contact using Fluorescence Microscopy.
International Journal of Technology, Volume 12(4), pp. 781–790
Raptis, K.G., Savaidis, A.A., 2018. Experimental
Investigation of Spur Gear Strength Using Photoelasticity. Procedia
Structural Integrity, Volume 10, pp. 33–40
Sharma,
A., Moorthy, H., Kumar, P., 2015. Stress Variation Due To Change In Centre
Distance Of Spur Gears Using Finite Element Analysis. In: International
Conference on Computer Aided Engineering (CAE), pp. 119–124
Wu,
Y., Wang, J., Han, Q., 2012. Static/Dynamic Contact FEA and Experimental Study for
Tooth Profile Modification of Helical Gears. Journal of Mechanical Science
and Technology, Volume 26(5), pp. 1409–1417
Y?lmaz,
T.G., Dogan, O., Karpat, F., 2017. Stress Analysis of Thin Rimmed Spur Gears with
Asymmetric Trochoid. In: Proceedings of the 3rd World Congress on Mechanical,
Chemical, and Material Engineering (MCM'17), p. 132
