Comparative Study of The Seismic Performance Between Simply Supported PSC Box Girder Bridge Equipped with Shear Panel Damper and Lead Rubber Bearing
Corresponding email: ali.awaludin@ugm.ac.id
Published at : 18 Sep 2024
Volume : IJtech
Vol 15, No 5 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i5.5750
Santoso, A.K., Sulistyo, D., Awaludin, A., Setiawan, A.F., Satyarno, I., Purnomo, S., Harry, I., 2024. Comparative Study of The Seismic Performance Between Simply Supported PSC Box Girder Bridge Equipped with Shear Panel Damper and Lead Rubber Bearing. International Journal of Technology. Volume 15(5), pp. 1321-1330
| Alvin Kurniawan Santoso | Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Djoko Sulistyo | Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Ali Awaludin | Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Angga Fajar Setiawan | Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Iman Satyarno | Department of Civil and Environmental Engineering, Faculty of Engineering, Universitas Gadjah Mada, Yogyakarta, 55281, Indonesia |
| Sidiq Purnomo | Engineering Section, PT. Wijaya Karya Beton Tbk., Boyolali, 57300, Indonesia |
| Ignatius Harry | Engineering Section, PT. Wijaya Karya Beton Tbk., Boyolali, 57300, Indonesia |
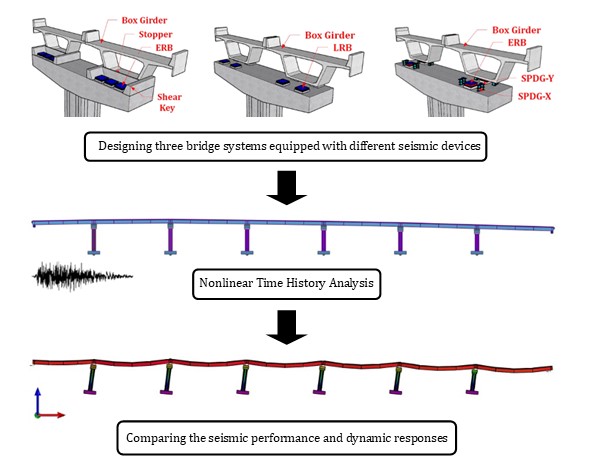
Several bridges in Indonesia are designed using
elastomeric bearing (ERB) with a low capability of reducing seismic responses.
This results in a significant demand for larger pier cross-sectional dimensions
and a greater number of reinforcements, necessitating the consideration of
seismic isolation devices to optimize the pier configuration. Lead rubber
bearing (LRB) has been widely used as a seismic isolation device due to the
natural period shifting and sufficient energy dissipation, but it costs a lot.
A shear panel damper equipped with a gap (SPDG) was proposed regarding its
capability to provide high damping at low cost as an alternative device to LRB.
This study compared the seismic performance of three structural systems of
simply supported prestressed concrete (PSC) box girder bridges. Those were
analyzed using Nonlinear Time History Analysis (NLTHA) with the OpenSees
software. As a result, both SPDG and LRB increased the structural flexibility
and generated similar relative pier responses to the conventional bridge with
ERB. For example, SPDG generated the relative responses of the top pier
displacement, base shear, and bending moment up to 64.76%, 83.55%, and 65.66%,
while LRB was 64.92%, 83.39%, and 66.89%, respectively. Meanwhile, the bridge’s
structural performance equipped with LRB and SPDG showed a fully operational
and operational limit, while the one with ERB reached the life safety limit due
to the longitudinal earthquake. The life safety limit due to the transverse
earthquake was also observed in the three bridge models. In conclusion, SPDG is
applicable in the seismic isolation system as it has a similar performance to
the LRB.
Elastomeric Rubber Bearing; Lead Rubber Bearing; Nonlinear Time History Analysis; Simply supported bridge; Shear Panel Damper Plus Gap
The role of seismic isolation devices is crucial in
accommodating the deformation of superstructures caused by earthquake forces.
Unfortunately, many bridges in Indonesia are equipped with elastomeric bearings
(ERB), which have low damping and limited seismic capacity. This leads to a
significant force demand being transmitted to the piers (Xiang, Goto, and
Alam, 2021; Xiang, Alam, and Li, 2019) and
increases the cross-sectional area as well as the number of pier reinforcements
to provide uniform seismic resistance. To optimize the design and minimize pier damage, it is necessary to utilize seismic
isolation devices with high damping, such as lead
rubber bearings (LRB) (Edalathi and Tahghighi,
2019; Sugihardjo et al., 2010).
Meanwhile, despite the fact that Indonesia is an earthquake-prone area, many
practicing engineers would rather use ERB instead of LRB due to budget
constraint. This increases the anxiety of many people regarding the structural
safety during strong earthquakes. Besides, the application of LRB would require
more effort for design and manufacture. Therefore, this study proposed a shear
panel damper equipped with a gap (SPDG), as it has a low cost with high damping
and a large seismic capacity (Nakashima et al., 1994) to overcome the disadvantages of LRB. Moreover, the proposed device could be easily replaced
without lifting the superstructure because the installation was accompanied by
other devices that provided vertical load capacity (Xiang,
Alam, and Li, 2019).
LRB acts as a bilinear elastic-plastic (Hameed
et al. 2008; Naeim and Kelly, 1999) with maximum deformation of 250% (Hamaguchi et
al., 2019; AASHTO, 2014). Meanwhile, the
behavior of the shear panel damper (SPD) is influenced by its web, which is
typically constructed using low-yield or mild steels with high ductility,
allowing it to deform easily up to a certain deformation limit (Yao,
Wang, and Zhu 2021; Zhang et al., 2013). In a study conducted by Liu, Aoki, and Shimoda (2013), it was found that SPD with a square plate and flange
deformed by 16-25%. Awaludin et al. (2022) developed SPD with a rectangular hollow shape that
laterally deformed up to 15% of the body height, and a stable post-yield
resistance was obtained when the web depth-thickness ratio was 25. Furthermore,
the SPD’s web was vulnerable to buckle due to the vertical load and needed to
be supported by ERB to provide an equitable vertical load capacity. This ERB
also provides lateral stiffness with 100% maximum deformation in the elastic
behavior (Yenidogan, 2021). Setiawan
and Takahashi (2018) also found that
the use of gaps in friction dampers reduced the structural stiffness without
any force resistance below the gap length. This simply means that the gap needs
to be applied to SPD to increase structural flexibility (Setiawan,
2018).
The previous study concluded that the application of LRB
increased the flexibility of a simply supported bridge and protected the pier
from more severe damage (Santoso et al., 2022;
Santoso, 2022). In this study, three structural systems of
simply supported prestressed concrete (PSC) box girder bridges are compared
using numerical analysis. This bridge is located in Makassar, Indonesia, and is
classified as a critical bridge according to SNI 2833:2016 (BSN,
2016). Several analytical methods have been employed
to investigate seismic performance, such as Nonlinear Time History Analysis
(NLTHA), pushover analysis, and modal analysis. NLTHA was performed to simulate
the structure’s dynamic response by applying five selected and scaled ground
motion records. A pushover analysis was conducted to determine the actual
pier’s capacity, while a modal analysis was performed to obtain structural
flexibility.
2.1. Bridge Modeling
Figure 2 Bridge model: (a) Model A, (b)
Model B, (c) Model C, and (d) Pier cross-section
Figure 3 SPDG mechanism based on Setiawan and
Takahashi (2018)
2.2. Ground Motion Modification
Five
selected earthquakes were classified as far-fault events, as the bridge is
situated in Makassar with an epicentral distance exceeding 10 km from the
earthquake source. This classification is based on the deaggregation analysis
of the Makassar earthquake as outlined in the study conducted by Sunardi and Nugraha (2016). ASCE (2010) allows for the selection of the ground motion
by considering the respective similar spectral shape of the designed bridge in
such a way that the allowable range of magnitude (Mw), fault
distance (R), source mechanism, and site class were relaxed. Moreover,
the magnitude, which is 5, fault distance
500 km, and shallow crustal
mechanism (strike-slip and reverse) were still considered based on the BMKG
earthquake repository described by Sunardi and
Nugraha (2016) as a lack of
references on the deaggregation of Makassar earthquake. Meanwhile, site class D
of soil represented by Vs30 in the range of 175–350 m/s was
determined based on the soil investigation report of the specific bridge
location. The amplitude scaling method was used to modify the ground motion
selected, and a single scale factor was applied to preserve the variation of
earthquake energy with the fundamental period found in the original record (ASCE, 2017; ASCE, 2010; Kalkan and Chopra, 2010).
2.3. Limit State
The performance level
is an indicator for observing and evaluating the structural performance
simultaneously and an instrument for ensuring structural capability during
service life. NCHRP (2013) classified the performance level into five
categories, also known as damage levels, as shown in Table 1. The determination
of the level depends on several parameters, which include steel strain,
concrete strain, and drift ratio. The damage levels I to IV are still
repairable. Meanwhile, level V required component replacement. So, the
performance level of fully operational (FO), operational (O), life safety (LS),
near collapse (NC), and collapse limits (C) are equivalent to damage levels.
3.1. Structural
Systems Comparison
This study incorporated
three parameters as design criteria for predicting the seismic responses of
isolated structures. These parameters are the stiffness ratio, yield strength
ratio, and ultimate strength ratio, which are utilized to control the seismic
behavior. Furthermore, pushover analysis was used to determine the pier
strength and stiffness parameters, while the formula proposed by AASHTO (2014) and Chen, Ge, and Usami (2007) ware used to calculate the seismic device.
The pier’s elastic stiffness
was observed to be less than the effective stiffness of all seismic devices
because its ratio exceeded one, as shown in Figure 4(a). However, the energy
dissipation started when the yield and the inelastic deformation occurred in
the seismic device. In Figure 4(b), the yield strength ratios of Models B and C
were below one, meaning that the initial yield of the structural system
occurred in the seismic devices rather than the pier. The ratio between the
maximum strength of the seismic devices and the pier is shown in Figure 4(c),
of which the ratios of Models B and C were above one. This implies the pier
potentially collapsed before the seismic devices failed. This makes the design
of an optimal isolated bridge system based on the basic concept to be
difficult, as the demand force has to be calculated to prevent the devices from
failing. Meanwhile, the yield strength ratio was considered an appropriate
design approach for seismic isolation devices.
Figure 4 (a) stiffness ratio, (b) yield strength ratio, (c)
ultimate strength ratio
3.2. Dynamic Responses Comparison
The effectiveness of the
seismic isolation device application was evaluated by considering the maximum
relative percentage of the pier responses, such as displacement, base shear,
and bending moment. The percentage was calculated by comparing the maximum
responses of the seismic-equipped bridge systems in Models B and C with the
conventional bridge system in Model A. The results of Models A and B were
obtained from Santoso et al. (2022), while Model C was
compared to the previous results.
Figure 5(a) shows a
comparison of the maximum top pier displacement in three models, represented by
pier P9. It was observed that the longitudinal displacements were smaller
compared to the transverse. In this case, all piers have rectangular
cross-sections with the same stiffness in both lateral directions, as shown in
Figure 2(d). Therefore, the reason is that a free cantilever pier in the
transverse direction provided less stiffness than those in the longitudinal
that was supported by a series of piers. Furthermore, the longitudinal
displacements in Model A were the largest of the other models, but some
transverse displacements in Model C were larger than in Model A based on some
earthquakes. This was influenced by the larger lateral stiffness and the yield
strength ratio of the bearing system to the substructure, where Model C was
larger than Model B, as shown in Figure 4. Besides, the bridge system with SPDG
generated the maximum relative displacement of 64.76% and 36.75%, while the one
with LRB showed 64.92% and 45.92% in the longitudinal and transverse
directions, as shown in Table 2.
Models B and C consistently show lower base shear results compared to
Model A, as shown in Figure 5(b). The seismic devices were capable of reducing
the spectral acceleration, while the larger pier in Model A produced stiffer
piers, thereby resulting in a greater base shear than the other models.
Meanwhile, both Models B and C showed comparable relative base shear, as
summarized in Table 3. The relative base shears in Models B and C reached
83.39% and 83.55% in the longitudinal directions, as well as 63.66% and 60.60%
in the transverse directions, respectively. In manual calculation, the maximum
shear capacity of Model A pier was 38740.32 kN, while Models B and C piers were
27377.12 kN. It was observed that the piers in all models did not exceed the
maximum shear capacity, meaning that the shear yielding did not occur.
Table 2 Top pier relative
displacement in longitudinal (X) and transverse (Y) directions
|
Model |
Maximum
Relative Displacement X (%) |
Maximum
Relative Displacement Y (%) | ||||||||||
|
P8 |
P9 |
P10 |
P11 |
P12 |
P13 |
P8 |
P9 |
P10 |
P11 |
P12 |
P13 | |
|
B |
58.2 |
55.2 |
57.7 |
56.7 |
55.6 |
64.9 |
28.9 |
24.8 |
45.9 |
24.7 |
44.1 |
28.0 |
|
C |
55.2 |
41.3 |
40.7 |
34.7 |
35.6 |
64.8 |
13.5 |
5.4 |
36.8 |
7.2 |
28.0 |
17.7 |
Table 3 Relative base shear
in longitudinal (X) and transverse (Y) directions
|
Model |
Maximum
Relative Base Shear X (%) |
Maximum
Relative Base Shear Y (%) | ||||||||||
|
P8 |
P9 |
P10 |
P11 |
P12 |
P13 |
P8 |
P9 |
P10 |
P11 |
P12 |
P13 | |
|
B |
76.4 |
76.7 |
77.1 |
78.7 |
81.3 |
83.4 |
60.5 |
55.9 |
56.5 |
58.5 |
63.7 |
61.4 |
|
C |
74.7 |
72.5 |
72.7 |
74.8 |
78.5 |
83.6 |
54.0 |
43.3 |
50.7 |
50.3 |
60.6 |
58.9 |
Table 4 Relative bending
moment in longitudinal (X) and transverse (Y) directions
|
Model |
Maximum
Relative Bending Moment X (%) |
Maximum
Relative Bending Moment Y (%) | ||||||||||
|
P8 |
P9 |
P10 |
P11 |
P12 |
P13 |
P8 |
P9 |
P10 |
P11 |
P12 |
P13 | |
|
B |
60.6 |
60.5 |
61.5 |
60.7 |
59.8 |
66.9 |
43.2 |
39.4 |
48.6 |
40.1 |
44.2 |
39.1 |
|
C |
58.2 |
50.1 |
50.1 |
45.5 |
46.2 |
65.6 |
32.4 |
31.7 |
45.4 |
29.7 |
39.6 |
32.6 |
3.3. Seismic Performance and Damage Comparison
The top pier displacement and curvature responses are two indicators for
measuring pier performance and damage. Table 5 shows the summary of the maximum
top pier displacements and performance levels in each pier. It was observed
that Models B and C showed better performances compared to Model A,
particularly in the longitudinal direction. This means that fully operational
limits were obtained in Models B and C, while Model A was in the life safety
limit state. It is important to note that life safety limit states were also
observed in all models due to the transverse earthquakes. In addition, damage
levels I and II were displayed in Models B and C, while damage level III was
shown in Model A due to longitudinal earthquakes. Table 5 also shows that all
bridge models reached damage level III due to transverse earthquakes.
Therefore, the application of SPDG was able to provide comparable performance
and protect the pier from more severe damage, just as in the bridge equipped
with LRB.
3.4. Seismic Device Responses
Figure 7 Seismic device’s responses on pier P9 due to
the transverse earthquakes
Three bridge models with
different structural systems have been investigated in this study using
numerical analysis. The results showed that the bridge models with seismic
devices, such as SPDG and LRB, were more flexible compared to the conventional
bridge equipped with ERB. Basically, SPDG started to dissipate seismic energy
when the deformation exceeded the gap length then the metal web experienced
yielding. The yielding state initiated an inelastic behavior that provided low
post-yield stiffness to accommodate the superstructure’s deformation.
Meanwhile, the designed gap allowed the device to deform at a zero-stiffness
state that increased the maximum shear strain capacity by 3% to prevent
failure. As a result, piers in the bridge with SPDG have comparable responses
to LRB. The relative responses to the conventional bridge, i.e., top pier
displacement, base shear, and bending moment, generated up to 64.76%, 83.55%,
and 65.66%, while LRB generated up to 64.92%, 83.39%, and 66.89%, respectively.
The practical design of isolated bridges with SPDG was also made easy when the
appropriate parameters were defined based on the target performance. Therefore,
the yield strength ratio needs to be considered as a criterion for designing
the SPDG and predicting the structural responses due to seismic excitation. It
was observed that the bridge with SPDG, which was designed in the yield
strength ratio’s range of 0.53–0.73, showed comparable seismic performance to
the bridge with LRB. Those were fully operational and operational limits due to
the longitudinal earthquakes, and life safety limit due to the transverse
earthquakes. In addition, the influence of vertical direction earthquakes will
increase vertical deformation. Consequently, the friction between two-separated
plates on the top of SPDG potentially occurred. This might inflict a large
buckling displacement and influenced the hysteretic behavior. Thus, it should
be considered while designing the vertical gap of SPDG.
The authors are grateful to the Department of Civil and Environmental
Engineering at Universitas Gadjah Mada and PT. Wijaya Karya Beton Tbk. for the
data support.
American
Association of State Highway and Transportation Officials (AASHTO), 2012. LRFD
Bridge Design Specifications. American Association of State Highway and
Transportation Officials, Washington, USA
American
Association of State Highway and Transportation Officials (AASHTO), 2014. Guide
Specifications for LRFD Seismic Bridge Design, 2nd Edition. American
Association of State Highway and Transportation Officials. Washington, USA
American
Society of Civil Engineers (ASCE), 2010. ASCE 7-10: Minimum Design
Loads for Buildings and Other Structures. American Society of Civil
Engineers, Virginia, USA
American
Society of Civil Engineers (ASCE), 2017. ASCE 7-16: Seismic
Evaluation and Retrofit of Existing Buildings. American Society of Civil
Engineers, Virginia, USA
Awaludin, A.,
Setiawan, A.F., Satyarno, I., Wu, S., Haroki, Y., 2022. Finite Element Analysis
of Bi-directional Shear Panel Damper with Square Hollow Section under Monotonic
Loading. Journal of the Civil Engineering Forum, Volume 8(2), pp. 157–168
Badan Standardisasi Nasional (BSN), 2016. SNI 2833:2016
Seismic Design of Bridge. Badan
Standardisasi Nasional, Jakarta, Indonesia
Berry, M.P., Eberhard, M.O., 2008. Performance Modeling Strategies for
Modern Reinforced Concrete Bridge Columns. Report PEER 2007/07, Pacific
Earthquake Engineering Research Center, Berkeley, California
Carreno, R., Lotfizadeh, K.H., Conte, J.P., Restrepo, J.I., 2019. Material
Model Parametes for The Giuffre-Menegotto-Pinto Uniaxial Steel Stress-Strain
Model. Journal of Structural Engineering, Volume 146, pp. 1 – 21
Chen, W., Duan, L., 2014. Bridge Engineering Handbook 2nd Edition, Seismic Design. CRC Press, New York, USA
Chen, Z., Ge, H., Usami, T., 2007. Study on
Seismic Performance Upgrading for Steel Bridge Structures by Introducing
Energy-dissipation Members. Journal of Structural Engineering, Volume
53A, pp. 540–549
Edalathi, A.A., Tahghighi, H., 2019.
Investigating The Performance of Isolation Systems inn Improving the Seismic
Behavior of Urban Bridge. Archives of Civil Engineering, Volume 65, pp.
155 – 175
Fillippou, F., Popov, E., Bertero, V., 1983. Effects
of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints.
Report EERC 83-19, Pacific Earthquake Engineering Research Center, Berkeley,
California
Hamaguchi, H., Wake, T., Yamamoto, M., Kikuchi,
M., 2019. Practical Application of Lead Rubber Bearings with Fail-safe
Mechanism. Journal of Structural and Construction Engineering, Volume
12, pp. 187 – 196
Hameed, Koo, M., Do, T.D., Jeong, J. Effect of
Lead Rubber Bearing Characteristics on The Response of Seismic-isolated
Bridges. KSCE Journal of Civil Engineering, Volume 12(3), pp. 187-196
Kalkan, E., Chopra, A.K., 2010. Practical
Guidelines to Select and Scale Earthquake Records for Nonlinear Response
History Analysis of Structures. Report 2010-1068, U.S. Geological Survey,
California, USA
Kappos A.J., Saiidi, M.S., Aydinoglu, M.N.,
Isacovic, T., 2012. Seismic Design and Assessment of Bridges, Springer, New
York, USA
Liu, Y., Aoki, T., Shimoda, M., 2013. Strain
Distribution Measurement of a Shear Panel Damper Developed for Bridge
Structure. Journal of Structures, Volume 2013, pp. 1–11
Mander, J.B., Priestley, M.N.J., Park, R.,
1988. Theoretical Stress-strain Model for Confined Concrete. Journal of
Structural Engineering, Volume 144, pp. 1804-1826
Menegotto, M., Pinto, P., 1973. Method of
Analysis for Cyclically Loaded RC Plane Frames Including Changes in Geometry
and Non-elastic Behavior of Elements Under Combined Normal Force and Bending.
IABSE Symposium on Resistance and Ultimate Deformability of Structure Acted on
by Well Defined Repeated Loads: Proceeding, Volume 11, pp. 15 – 22
Naeim, F., Kelly, J.M.,
1999. Design
of Seismic Isolated Structures: From Theory to Practice. John Wiley & Sons Inc.,
New York, USA
Nakashima, M., Iwai, S., Iwata, M., Takeuchi,
T., Konomi, S., Akazawa, T., Saburi, K., 1994. Energy Dissipation Behavior of
Shear Panels Made of Low Yield Steel. Earthquake Engineering and Structural
Dynamics, Volume 23, pp. 1299-1313
National
Cooperative Highway Research Program (NCHRP), 2013. Performance-Based
Seismic Bridge Design: A Synthesis of Highway Practice. Transportation
Research Board, Washington, USA
Omrani, R.,
Mobasher, B., Liang, X., Gunay, S., Mosalam, K.M., Zareian, F., Taciroglu, E.,
2015. Guidelines for Nonlinear Seismic Analysis of Ordinary Bridge: Version
2.0. Report No. 15-65A0454, California Department of Transportation,
California, USA
Santoso, A.,
Sulistyo, D., Awaludin, A., Setiawan, A.F., Satyarno, I., Purnomo, S., Harry,
I., 2022. Structural Systems Comparison of Simply Supported PSC Box Girder
Bridge Equipped with Elastomeric Rubber Bearing and Lead Rubber Bearing. Civil
Engineering Dimension, Volume 24, pp. 19–30
Santoso, A.K., 2022. Perbandingan Penggunaan Shear Panel Damper dan Lead
Rubber Bearing untuk Meningkatkan Performa Seismik Struktur Jembatan Box Girder
Tumpuan Sederhana (Comparative Study on Seismic Performance Between Simply
Supported Box Girder Bridge Equipped with Shear Panel Damper and Lead Rubber
Bearing). Master’s Thesis, Graduate Program, Universitas Gadjah Mada,
Yogyakarta, Indonesia
Setiawan,
A.F., 2018. Development of High Seismic Performance Integrated Bridge Pier
Connected by Hysterical Damper, Doctor’s Dissertation, Graduate Program, Kyoto
University, Kyoto, Japan
Setiawan,
A.F., Takahashi, Y., 2018. A High Seismic Performance Concept of Integrated
Bridge Pier with Triple RC Columns Accompanied by Friction Damper Plus Gap. Journal
of Japan Society of Civil Engineers, Volume 74, pp. 131–147
Steelman J.,
Fahnnestock, L., Filipov, E., LaFave, J., Hajjar, J., Foutch, D., 2013. Shear
and Friction Response of Nonseismic Laminated Elastomeric Bridge Bearings
Subject to Seismic Demands. Journal of Bridge Engineering, Volume 18,
pp. 612 – 623
Sugihardjo,
H., Tavio, Manalu, I., Lesmana, Y., 2018. Seismic Study of Lead-Rubber Bearing
Application in Kutai Kertanegara Steel Arch Bridge. International Journal on
Advanced Science Engineering Information Technology, Volume 8, pp. 540 –
546
Sunardi, B.,
Nugraha, J., 2016. Peak Ground Acceleration at Surface and Spectral
Acceleration for Makassar City Based on A Probabilistic Approach. Jurnal Meteorologi dan Geofisika, Volume 17, pp 33–46
Vecchio, F.J., Collins, M.P., 1986. The
Modified Compression-field Theory for Reinforced Concrete Elements Subject to
Shear. Journal Proceedings, Volume 83, pp. 219-231
Xiang, N., Alam, M., Li, J., 2019. Yielding Steel
Dampers as Restraining Devices to Control Seismic Sliding of Laminated Rubber
Bearings for Highway Bridges: Analytical and Experimental Study. Journal of
Bridge Engineering, Volume 24(11), pp. 1–15
Xiang, N., Goto, Y., Alam, M., Li, J., 2021.
Effect of Bonding or Unbonding on Seismic Behavior of Bridge Elastomeric
Bearings: Lessons Learned from Past Earthquakes in China and Japan and
Inspirations for Future Design. Advances in Bridge Engineering, Volume
2(1), pp. 1-17
Yao, Z., Wang, W., Zhu, Y., 2021. Experimental
Evaluation and Numerical Simulation of Low-yield-point Steel Shear Panel
Dampers. Engineering Structures, Volume 245, pp. 1-17
Yenidogan, C.,
2021. Earthquake-Resilient Design of Seismically Isolated Buildings: A Review
of Technology. Vibration, Volume 4, pp. 602–647
Zhang, C.,
Zhang, Z., Aoki, T., Zhang, M., 2013. Research on The Dynamic Performance of
Low-Yield-Strength Shear Panel Damper for Bridge Application. Journal of
Shanghai Jiaotong University, Volume 18, pp. 118 – 128
