Simulation-Based Optimization of Injection Molding Process Parameters for Minimizing Warpage by ANN and GA
Published at : 04 Apr 2023
Volume : IJtech
Vol 14, No 2 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i2.5573
Nitnara, C., Tragangoon, K., 2023. Simulation-Based Optimization of Injection Molding Process Parameters for Minimizing Warpage by ANN and GA. International Journal of Technology. Volume 14(2), pp. 422-433
| Chiwapon Nitnara | Department of Mechanical Engineering Technology, College of Industrial Technology, King Mongkut's University of Technology North Bangkok, 1518 Pracharat I, Bangsue, Bangkok 10800, Thailand |
| Kumpon Tragangoon | Department of Mechanical Engineering Technology, College of Industrial Technology, King Mongkut's University of Technology North Bangkok, 1518 Pracharat I, Bangsue, Bangkok 10800, Thailand |
Plastic injection molding is one of the most used
methods for producing plastic products because it can be produced at a high
production rate, low cost, and ease in manufacturing. However, one defect that
affects product quality is namely warpage. To reduce plastic product warpage,
the injection molding process is required optimal process control to
increase plastic product quality. The objective of this paper is to optimize
injection molding process parameters for minimizing the warpage of plastic
glass. The optimization process is divided into two phases.
The Finite Element Method (FEM) was employed in the first phase to
simulate 32 experiments under various parameters. The parameters of this
process consist of melt temperature ranging from 180 to 230 °C, mold
temperature in the range of 20 – 45 °C, filling time from 0.82 to 0.92 s,
packing time ranging from 5.88 to 7 s and cooling time of 14 to 18 s. In the
second phase, Artificial Neural Network (ANN) combined Genetic Algorithm (GA)
was developed to predict the warpage and solve the optimization process to find
optimal parameters. Combining the intelligent method shows that ANN and GA
effectively find the optimal process parameters that can reduce the warpage of
the product by 35.73% from the maximum value.
Artificial Neural Network (ANN); Finite Element Method (FEM); Genetic Algorithm (GA); Optimization; Plastic injection molding
Plastic
injection molding is the most popular process for producing plastic packaging,
medical equipment, automotive parts, and electronics. In the plastic injection
molding process, the plastic pellets are melted at high temperatures by a
heater of the injection machine. Subsequently, melted plastic is injected into
the mold cavity and core with specific injection pressure and packed by packing
pressure. Finally, the melted plastic is cooled down to transform into a
plastic product (Kitayama et al., 2020; Cheng
and Liu, 2018; Hasnan et al., 2017).
However, the process parameters, such as the melt temperature of the plastic,
injection pressure, packing pressure, packing time, and cooling time, affect
the resulting product's properties. The properties of plastic products from the
injection molding process are required a high strength-to-weight ratio and
durability. Controlling the process parameters is necessary for obtaining the
best plastic product property.
Traditionally, the conventional practice of determining injection molding
process parameters is adjusted through trial and error by experienced engineers
(Guo et al., 2019). However, this
method cannot precisely determine the optimal process parameters, resulting in
time-consuming, repetitive testing and easy occurring defect. The most common
type of defect that occurs in the plastic injection molding process is called
warpage which affects the quality of the product (Huang
et al., 2021; Gao
and Wang, 2008; Kurtaran and Erzurumlu,
2006; Hakimian and Sulong, 2012). The warpage of the product continues
occurring because several related process parameters and independent process
parameters intervene with the plastic injection molding process.
Computer-aided engineering
(CAE) was a technology for numerical simulation of the plastic injection
molding process (Hentati et al., 2019).
The advantage of CAE was less cost and faster experimenting virtually.
Additionally, CAE serves as a tool for predicting the behavior of defects that
may impact the product's quality, as well as for the validation and
optimization of the product's design. At present, the intelligent method is
widely used in combination with CAE to optimize the plastic injection molding
process for reducing defects such as artificial neural networks, genetic
algorithms, support vector machine, Etc (Zhao et
al., 2020).
Several studies have
investigated the optimization of the injection molding process by different
techniques. Shi, Xie, and Wang (2013) optimized plastic injection process parameters to reduce warpage by using
the Kriging surrogate model. Erzurumlu and Ozcelik
(2006) minimized warpage and sink marks of plastic parts under different
design rib cross-section types and rib layout angles by using Taguchi
optimization. Oliaei et al. (2016) optimized
plastic injection process parameters by Taguchi's orthogonal array, and ANN was
selected as the optimal parameter. Zhang et al.
(2016) presented particle swarm optimization on the oil cooler cover cooling
and a cooling channel to reduce warpage. Zhou, Turng,
and Kramschuster (2006) used SVR and GA to optimize the process
parameters. Dang (2014) used direct and
metamodel-based methods as optimization injection molding process parameters. Farshi, Gheshmi, and Miandoabchi (2011) presented
the Evolutionary Operation (EVOP) method used to minimize the warpage and
shrinkage defects of plastic parts. Lockner and
Hopmann (2021) used network-based transfer learning to reduce data of
artificial neural network training for optimizing injection machine parameters.
The objective of this paper
is to find the optimal injection molding process parameters for reducing
warpage by determining the injection molding process parameters of plastic
glass. we conducted experiments using a simulation method to assess warpage
under various process parameters, including melt temperature, mold temperature,
filling time, packing time, and cooling time. To further refine our results, we
used artificial neural networks (ANN) to predict warpage based on simulation
data and developed a Fitness Function Equation. Finally, we utilized the GA
method to identify the optimal injection molding process parameters that will
reduce warpage in plastic glass.
2.1. Sample Part
In this experiment, the part is a plastic glass used for an experimental simulation. The dimensions have a diameter of 97 mm, height of 70 mm, and thickness of 2 mm. Plastic glass is made of polystyrene (PS), which is widely used in consumer goods and commercial packaging. The general view of the part is presented in (Figure 1).
Figure 1 Plastic Glass
2.2. Experiment
The
Finite Element Method (FEM) was developed to simulate the behavior of plastic material
(Hashash, Jung, and Ghaboussi, 2004; Hung, Chen, and Lin, 2002). In addition, the FEM capability can
help improve the defects that may occur before actual production (Irsyad et al., 2020). A MOLDEX 3D software
was used to simulate the plastic injection molding process to determine the
defect of the sample part. This software uses the Finite Element Method to
analyze the plastic behavior of the injection molding process by a mathematical
function. In this simulation, various parameters are adjusted to determine the
minimum warpage value.
The experiment
simulation was created by the design of the experiment (DOE) method with 32
experiments. The process parameters of injection molding experiments consist of
the melt temperature, mold temperature, filling time, packing time, and cooling
time were chosen as input parameters as shown in Table 1.
Table
1 Process parameters
|
Process parameters |
Level | |
|
Low |
High | |
|
Melt temperature (degree) |
180 |
230 |
|
Mold Temperature (degree) |
20 |
45 |
|
Filling Time (mm/s) |
0.82 |
0.94 |
|
Packing Time (s) |
5.88 |
7 |
|
Cooling Time (s) |
14 |
18 |
2.3. Warpage
The warpage is a distortion of the dimension part on 3 axes consisting
of x, y, and z from the actual dimension of the part. Adjusting suitable
injection molding process parameters is essential to decrease the warpage of
parts, which is the main purpose of this paper. The warpage was measured as the
total displacements on 3 axes of the product. An equation for the warpage is (Mukras, Omar, and al-Mufadi, 2019):
TWsum =
? ymax i (1)
i = 1, 2, 3
where ymaxi is the
displacement on one axis of the product.
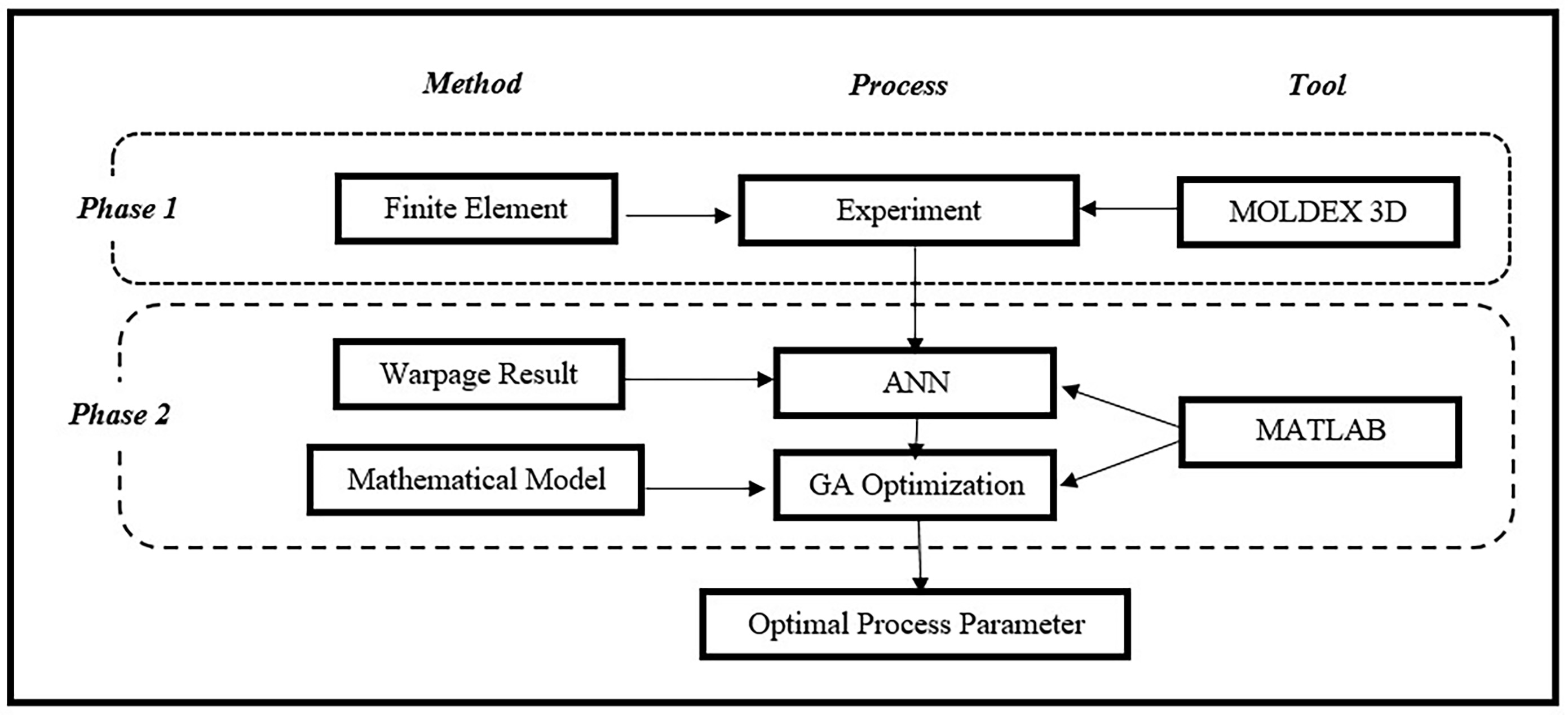
This paper consists of two phases: First, a simulation of injection molding process experiments. It has 32 experiments under different parameter setting values to determine the warpage value. Second, ANN has conducted predicted warpage from the simulation result of the experiment. The result from predicting the warpage value of ANN has created a mathematical model by coefficient value for fitness function of GA. Optimization by the GA method was performed to find the optimal injection molding parameter using a mathematical model from the ANN method, which results in the lowest warpage. (Figure 2) shows the process of this paper.
Figure 2 Process of paper
3.1. Simulation
Moldex3D software was used
in this experiment to simulate the injection molding process (Sun et al., 2021; Quintana and Frontini, 2020; Tseng,
Chang, and Hsu, 2017) with 32 experiments in order to find out the
warpage value. Table 2 shows results gained from the simulation, and mold base
for analysis were used for the ANN method. (Figure 3) depicts the maximum
warpage result that occurs on the red color area of the example plastic glass
in experiment No. 1, which is 0.809 mm after the experiment simulation was
conducted, and the mold base for analysis has 8 cooling channels used to heat
transfer.
Table 2 Results of experiments simulation
|
No. |
Melt Temperature |
Mold Temperature |
Filling Time |
Packing Time |
Cooling Time |
Warpage | |||||||
|
1 |
180 |
20 |
0.82 |
5.88 |
14 |
0.809 | |||||||
|
2 |
230 |
20 |
0.82 |
5.88 |
14 |
1.119 | |||||||
|
3 |
180 |
45 |
0.82 |
5.88 |
14 |
0.848 | |||||||
|
4 |
230 |
45 |
0.82 |
5.88 |
14 |
1.205 | |||||||
|
5 |
180 |
20 |
0.94 |
5.88 |
14 |
0.823 | |||||||
|
6 |
230 |
20 |
0.94 |
5.88 |
14 |
1.122 | |||||||
|
7 |
180 |
45 |
0.94 |
5.88 |
14 |
0.854 | |||||||
|
8 |
230 |
45 |
0.94 |
5.88 |
14 |
1.198 | |||||||
|
9 |
180 |
20 |
0.82 |
7 |
14 |
0.801 | |||||||
|
10 |
230 |
20 |
0.82 |
7 |
14 |
1.09 | |||||||
|
11 |
180 |
45 |
0.82 |
7 |
14 |
0.842 | |||||||
|
12 |
230 |
45 |
0.82 |
7 |
14 |
1.154 | |||||||
|
13 |
180 |
20 |
0.94 |
7 |
14 |
0.828 | |||||||
|
14 |
230 |
20 |
0.94 |
7 |
14 |
1.124 | |||||||
|
15 |
180 |
45 |
0.94 |
7 |
14 |
0.84 | |||||||
|
16 |
230 |
45 |
0.94 |
7 |
14 |
1.165 | |||||||
|
17 |
180 |
20 |
0.82 |
5.88 |
18 |
0.8 | |||||||
|
18 |
230 |
20 |
0.82 |
5.88 |
18 |
1.096 | |||||||
|
19 |
180 |
45 |
0.82 |
5.88 |
18 |
0.843 | |||||||
|
20 |
230 |
45 |
0.82 |
5.88 |
18 |
1.176 | |||||||
|
21 |
180 |
20 |
0.94 |
5.88 |
18 |
0.815 | |||||||
|
22 |
230 |
20 |
0.94 |
5.88 |
18 |
1.09 | |||||||
|
No. |
Melt Temperature |
Mold Temperature |
Filling Time |
Packing Time |
Cooling Time |
Warpage |
| ||||||
|
23 |
180 |
45 |
0.94 |
5.88 |
18 |
0.845 |
| ||||||
|
24 |
230 |
45 |
0.94 |
5.88 |
18 |
1.162 |
| ||||||
|
25 |
180 |
20 |
0.82 |
7 |
18 |
0.795 |
| ||||||
|
26 |
230 |
20 |
0.82 |
7 |
18 |
1.076 |
| ||||||
|
27 |
180 |
45 |
0.82 |
7 |
18 |
0.834 |
| ||||||
|
28 |
230 |
45 |
0.82 |
7 |
18 |
1.115 |
| ||||||
|
29 |
180 |
20 |
0.94 |
7 |
18 |
0.812 |
| ||||||
|
30 |
230 |
20 |
0.94 |
7 |
18 |
1.097 |
| ||||||
|
31 |
180 |
45 |
0.94 |
7 |
18 |
0.835 |
| ||||||
|
32 |
230 |
45 |
0.94 |
7 |
18 |
1.129 |
| ||||||
Figure 3
Simulation Analysis: (a)
Warpage; and (b) Mold base
3.2. Artificial Neural Network (ANN)
ANN is widely used in engineering because ANN ability can analyze
information by detecting data patterns and relationships through learning. It
is easier to analyze and improve engineering processes (Hemmati
et al., 2020; Alas and Ali, 2019;
Rafiq, Bugmann, and Easterbrook, 2001).
This section uses the ANN to predict the warpage results from the experiment simulation by MATLAB software. The experimental parameters are an input of ANN, consisting of melt temperature, mold temperature, filling time, packing time, and cooling time. During the network training, the weight (w) of the network is calculated by minimizing the error value between the predicted warpage value, which is called the output of ANN, and the actual warpage value (Chen et al., 2008; Lee and Lin, 2006; Sadeghi, 2000). (Figure 4) shows the ANN model consists of five inputs, the transfer function is sigmoid, ten hidden layers, and one output. A Backpropagation network (BPN) has been adopted because it has the ability of fast responsiveness and high accuracy (Asmael et al., 2022).
Figure 4
ANN Model
Using the warpage results
obtained by the simulation experiment to predict by ANN, Table 3 shows the
resulting warpage of ANN compared with the finite element method analysis of
the experiment.
Table
3 Results of ANN prediction
|
No. |
Melt Temperature |
Mold Temperature |
Filling Time |
Packing Time |
Cooling Time |
Warpage |
ANN Warpage |
|
1 |
180 |
20 |
0.82 |
5.88 |
14 |
0.809 |
0.804 |
|
2 |
230 |
20 |
0.82 |
5.88 |
14 |
1.119 |
1.028 |
|
3 |
180 |
45 |
0.82 |
5.88 |
14 |
0.848 |
0.847 |
|
4 |
230 |
45 |
0.82 |
5.88 |
14 |
1.205 |
1.223 |
|
5 |
180 |
20 |
0.94 |
5.88 |
14 |
0.823 |
0.846 |
|
6 |
230 |
20 |
0.94 |
5.88 |
14 |
1.122 |
1.022 |
|
7 |
180 |
45 |
0.94 |
5.88 |
14 |
0.854 |
0.87 |
|
8 |
230 |
45 |
0.94 |
5.88 |
14 |
1.198 |
1.248 |
|
9 |
180 |
20 |
0.82 |
7 |
14 |
0.801 |
0.81 |
|
10 |
230 |
20 |
0.82 |
7 |
14 |
1.09 |
1.102 |
|
11 |
180 |
45 |
0.82 |
7 |
14 |
0.842 |
0.847 |
|
12 |
230 |
45 |
0.82 |
7 |
14 |
1.154 |
1.148 |
|
13 |
180 |
20 |
0.94 |
7 |
14 |
0.828 |
0.813 |
|
14 |
230 |
20 |
0.94 |
7 |
14 |
1.124 |
1.118 |
|
15 |
180 |
45 |
0.94 |
7 |
14 |
0.84 |
0.838 |
|
16 |
230 |
45 |
0.94 |
7 |
14 |
1.165 |
1.216 |
|
17 |
180 |
20 |
0.82 |
5.88 |
18 |
0.8 |
0.809 |
|
18 |
230 |
20 |
0.82 |
5.88 |
18 |
1.096 |
1.1 |
|
19 |
180 |
45 |
0.82 |
5.88 |
18 |
0.843 |
0.846 |
|
20 |
230 |
45 |
0.82 |
5.88 |
18 |
1.176 |
1.137 |
|
21 |
180 |
20 |
0.94 |
5.88 |
18 |
0.815 |
0.821 |
|
22 |
230 |
20 |
0.94 |
5.88 |
18 |
1.09 |
1.084 |
|
23 |
180 |
45 |
0.94 |
5.88 |
18 |
0.845 |
0.86 |
|
24 |
230 |
45 |
0.94 |
5.88 |
18 |
1.162 |
1.126 |
|
25 |
180 |
20 |
0.82 |
7 |
18 |
0.795 |
0.789 |
|
26 |
230 |
20 |
0.82 |
7 |
18 |
1.076 |
1.063 |
|
27 |
180 |
45 |
0.82 |
7 |
18 |
0.834 |
0.827 |
|
28 |
230 |
45 |
0.82 |
7 |
18 |
1.115 |
1.105 |
|
29 |
180 |
20 |
0.94 |
7 |
18 |
0.812 |
0.819 |
|
30 |
230 |
20 |
0.94 |
7 |
18 |
1.097 |
1.066 |
|
31 |
180 |
45 |
0.94 |
7 |
18 |
0.835 |
0.818 |
|
32 |
230 |
45 |
0.94 |
7 |
18 |
1.129 |
1.168 |
The results showed that the mean square
error (MSE) of validation is 0.004, and the overall R-square value is 0.97985.
The mean square error (MSE) of ANN has a value of close to 0, and the R-square
is near 1. The average prediction error % of the ANN model was 1.97%. It
clearly shows that the ANN has a high performance in predicting the result of
the warpage as shown in (Figure
5).
Figure
5
ANN Model performance: (a) Validation; (b)
Overall data; and (c) Cross plot data
In this section, MATLAB software was
used to analyze coefficients of the multiple linear regression equation for the
objective function of GA. To create the mathematical model, a multiple linear
regression equation was established to show the relationship of the injection
molding processing parameters on the warpage by Equation 2 (Ozcelik and Sonat, 2009).
where y is the value of the warpage, is intercept,
are coefficients values
obtained from MATLAB software, x1, x2, …, xn
are process parameters factors.
3.3. Genetic Algorithm (GA) Optimization
GA is an
optimization technique that uses a randomized search method to achieve optimal
values. It is based on a model of a natural genetic selection mechanism that
has the ability to survive and pass on to the next generation (Eusuff, Lansey, and Pasha, 2006).
The optimization injection molding
process parameters problem in Equation 3 was solved by a GA created by the
MATLAB Optimization toolbox. The parameter value used for the GA is 100 for the
population size, 0.6 for the crossover rate, and 0.05 for the mutation rate.
The roulette wheel method was used to select the next generation. (Figure 6)
shows the GA optimization terminates at generation no. 140 from 500 generations,
which are the results of the objective function.
Minimize Warpage (Z). Z = (Melt Temperature, Mold Temperature, Filling
Time, Packing Time, Cooling Time);
Subject
to
180 Melt Temperature
230oC
20 Mold Temperature
45oC
0.82 Filling Time
0.94 mm/s (3)
5.88 Packing Time
7 mm/s
14 Cooling Time
18 s
Figure
6 Result of GA
optimization process parameter
From (Figure 6), the GA optimization process
parameters result include melt temperature of 192oC, mold temperature of 23oC,
filling time of 0.865 mm/s, packing time of 6.72 mm/s, and cooling time is 16 s
which affects warpage that is 0.770 mm. The process parameters of experiment
simulation no.8 consist of a melt temperature of 230oC, mold temperature of
45oC, filling time of 0.940 mm/s, packing time of 5.88 mm/s, and cooling time
is 14 s have a maximum warpage value of 1.198 mm compare with the result of GA
as shown in Table 4.
Table
4 Process parameter of
experiment simulation and GA
|
|
Melt
Temperature |
Mold Temperature |
Filling
Time |
Packing
Time |
Cooling
Time |
Warpage |
|
Experiment
Simulation |
230 |
45 |
0.940 |
5.88 |
14 |
1.198 |
|
GA |
192 |
23 |
0.865 |
6.72 |
16 |
0.770 |
To confirm the result of this method, the optimal plastic injection molding process of GA consists of a melt temperature of 192oC, mold temperature of 23oC, filling time of 0.865 mm/s, packing time of 6.72 mm/s, and cooling time is 16 s were simulated by MOLDEX3D software as shown in (Figure 7).
Figure
7 Confirmation optimal
process parameters
The confirmation result shows that the warpage of the simulation is 0.770 mm, which equal to the results of GA. When the maximum warpage of the experiment simulation is considered, it depicts the maximum warpage on a plastic glass of experiment simulation, which is 1.198 mm before the optimization. After optimization, it was found that the warpage is reduced to 0.770 mm, which is about 35.73% of the maximum warpage. (Figure 8) shows a comparison of the warpage experiment simulation with GA.
Figure 8 Result of GA optimization process parameter
The objective of this paper was to determine the optimal injection
molding process parameters for minimized plastic glass warpage through a Finite
Element, ANN and GA. The finite element method simulated five process
parameters (melt temperature, mold temperature, filling time, packing time, and
cooling time) for finding warpage under various parameters. The results of the
experiment simulation were used for predictive models were established using
ANN. The average prediction error of the ANN was 1.97%, with a mean square
error (MSE) of 0.004. It shows that obtained results showed good prediction
accuracy. After the prediction warpage by ANN, A mathematical was created for a
Fitness Function of GA. In the optimization process, GA was utilized for the
optimal selection of the plastic injection molding process parameters that
reduced the warpage of the product by 35.73% from the maximum warpage of the
simulation. It clearly shows that GA has high efficiency in finding the optimal
injection molding process parameters. Moreover, it is a guideline for
optimizing the process parameters of another plastic part with speed and
accuracy. However, this simulation with the finite element method is prediction
the behaviour of defects in the pre-production process where the simulation
process parameters are stable and independent from interference complications.
On the other hand, a higher defect value ??may occur in the experiment as other
factors such as machinery deterioration, air
humidity, and air temperature can easily intervene in the plastic injection molding process. Moreover,
the current simulation did not include optimization of the injection and
packing pressures by setting pressure following plastic melt flow behavior fill
to the mold impression in the setting pressure process of the injection
machine. The pressure values used in the simulation were based on the material
profile within the simulation software. Thus, determining appropriate pressure
values following plastic melt flow behavior may further enhance the efficiency
of reducing product warpage.
| Filename | Description |
|---|---|
| R1-IE-5573-20220502232944.pdf | --- |
Alas, M., Ali, S.I.A., 2019. Prediction of the high-temperature
performance of a geopolymer modified asphalt binder using artificial neural
networks. International Journal of Technology. Volume 10(2), pp.
417–427
Asmael, M., Nasir, T., Zeeshan, Q., Safaei, B., Kalaf, O.,
Motallebzadeh, A., Hussain, G., 2022. Prediction of properties of friction stir
spot welded joints of AA7075-T651/Ti-6Al-4V alloy using machine learning
algorithms. Archives of Civil and Mechanical Engineering, Volume
22(2), pp. 1–19
Chen, W.C., Tai, P.H., Wang, M.W., Deng, W.J., Chen, C.T., 2008. A
neural network-based approach for dynamic quality prediction in a plastic
injection molding process. Expert systems with Applications, Volume
35(3), pp. 843–849
Cheng, C.C., Liu, K.W., 2018. Optimizing energy savings of the
injection molding process by using a cloud energy management system. Energy
Efficiency, Volume 11(2), pp. 415–426
Dang, X.P., 2014. General frameworks for optimization of plastic
injection molding process parameters. Simulation Modelling Practice and
Theory, Volume 41, pp. 15–27
Erzurumlu, T., Ozcelik, B., 2006. Minimization of warpage and sink
index in injection-molded thermoplastic parts using Taguchi optimization
method. Materials & design, Volume 27(10), pp. 853–861
Eusuff, M., Lansey, K., Pasha, F., 2006. Shuffled frog-leaping
algorithm: a memetic meta-heuristic for discrete optimization. Engineering
optimization, Volume 38(2), pp. 129–154
Farshi, B., Gheshmi, S., Miandoabchi,
E., 2011. Optimization of injection molding process parameters using sequential
simplex algorithm. Materials & Design, Volume 32(1), pp.
414–423
Gao, Y., Wang, X., 2008. An effective warpage optimization method
in injection molding based on the Kriging model. The International
Journal of Advanced Manufacturing Technology, Volume 37, pp.
953–960
Guo, F., Zhou, X., Liu, J., Zhang, Y., Li, D., Zhou, H., 2019. 1A reinforcement
learning decision model for online process parameters optimization from offline
data in injection molding. Applied Soft Computing, Volume 85,
p.105828
Hakimian, E., Sulong, A.B., 2012. Analysis of warpage and shrinkage
properties of injection-molded micro gears polymer composites using numerical
simulations assisted by the Taguchi method. Materials & Design, Volume
42, pp. 62–71
Hashash, Y.M.A., Jung, S., Ghaboussi, J., 2004. Numerical
implementation of a neural network based material model in finite element
analysis. International Journal for numerical methods in engineering, Volume
59(7), pp. 989–1005
Hasnan, A., Putra, N., Septiadi, W.N., Ariantara, B., Abdullah,
N.A., 2017. Vapor chamber utilization for rapid cooling in the conventional
plastic injection molding process. International Journal of Technology, Volume
8(4), pp. 690–697
Hemmati-Sarapardeh, A., Varamesh, A., Amar, M.N., Husein, M.M.,
Dong, M., 2020. On the evaluation of thermal conductivity of nanofluids
using advanced intelligent models. International Communications in Heat
and Mass Transfer, Volume 118, p. 104825
Hentati, F., Hadriche, I., Masmoudi, N., Bradai, C., 2019.
Optimization of the injection molding process for the PC/ABS parts by
integrating Taguchi approach and CAE simulation. The International
Journal of Advanced Manufacturing Technology, Volume 104(9), pp. 4353–4363
Hung, C., Chen, R.H., Lin, C.R., 2002. The characterisation and finite-element
analysis of a polymer under hot pressing. The International Journal of
Advanced Manufacturing Technology, Volume 20, pp. 230-235
Huang, X. L., Yang, J. R., Sun, Y.X., Chen, Y.W., Wang, X.M., Du,
S.M., Hua, Z.K., 2021. Novel combined shield design for eye and face protection
from COVID-19. Advances in Manufacturing, Volume 9(1), pp. 130–135
Irsyad, M., Nadhif, M.H., Rahyussalim, A.J., Assyarify, H., Utomo,
M.S., 2020. Material Selection Techniques for Polymer Hubs of Novel Spinal Stem
Cell Introducers using Finite Element and Weighted Property Method. International
Journal of Technology. Volume 11(5), pp. 1056–1065
Kitayama, S., Hashimoto, S., Takano, M., Yamazaki, Y., Kubo, Y.,
Aiba, S., 2020. Multi-objective optimization for minimizing weldline and cycle
time using variable injection velocity and variable pressure profile in plastic
injection molding. The International Journal of Advanced Manufacturing
Technology, Volume 107(7), pp. 3351–3361
Kurtaran, H., Erzurumlu, T., 2006. Efficient warpage optimization
of thin shell plastic parts using response surface methodology and genetic
algorithm. The International Journal of Advanced Manufacturing
Technology, Volume 27(5), pp. 468–472
Lee, K. S., Lin, J. C., 2006. Design of the runner and gating
system parameters for a multi-cavity injection mold using FEM and neural
network. The International Journal of Advanced Manufacturing Technology, Volume
27(11-12), pp. 1089–1096
Lockner, Y., Hopmann, C., 2021. Induced network-based transfer
learning in injection molding for process modelling and optimization with
artificial neural networks. The International Journal of Advanced
Manufacturing Technology, Volume 112(11), pp. 3501–3513
Mukras, S.M., Omar, H.M., al-Mufadi, F.A., 2019. Experimental-based
multi-objective optimization of injection molding process parameters. Arabian
Journal for Science and Engineering, Volume 44(9), pp. 7653–7665
Oliaei, E., Heidari, B. S., Davachi, S. M., Bahrami, M., Davoodi,
S., Hejazi, I., Seyfi, J., 2016. Warpage and shrinkage optimization of
injection-molded plastic spoon parts for biodegradable polymers using taguchi,
ANOVA and artificial neural network methods. Journal of Materials
Science & Technology, Volume 32(8), pp. 710–720
Ozcelik, B., Sonat, I., 2009. Warpage and structural analysis of
thin shell plastic in the plastic injection molding. Materials &
Design, Volume 30(2), pp. 367–375
Quintana, M. C., Frontini, P., 2020. Weld line strength factors in
a reinforced injection molded part: Relationship with predicted fibre
orientation. Journal of Reinforced Plastics and Composites, Volume
39(5-6), pp. 219–230
Rafiq, M.Y., Bugmann, G., Easterbrook, D.J., 2001. Neural network
design for engineering applications. Computers & Structures, Volume
79(17), pp. 1541–1552
Sadeghi, B.H.M., 2000. A BP-neural network predictor model for
plastic injection molding process. Journal of materials processing
technology, Volume 103(3), pp. 411–416
Shi, H., Xie, S., Wang, X., 2013. A warpage optimization method for injection molding using artificial neural network with parametric sampling evaluation strategy. The International Journal of Advanced Manufacturing Technology, Volume 65(1-4), pp. 343–353
Sun, C., Gergely, R., Okonski, D.A., Min, J., 2021. Experimental
and numerical investigations on thermoforming of thermoplastic prepregs of
glass fibre reinforced nylon 6. Journal of Materials Processing
Technology, Volume 295, p. 117161
Tseng, H.C., Chang, R.Y., Hsu, C.H., 2017. Numerical prediction of
fibre orientation and mechanical performance for short/long glass and carbon
fibre-reinforced composites. Composites Science and Technology, Volume
144, pp. 51–56
Zhang, J., Wang, J., Lin, J., Guo, Q., Chen, K., Ma, L., 2016.
Multiobjective optimization of injection molding process parameters based on
Opt LHD, EBFNN, and MOPSO. The International Journal of Advanced
Manufacturing Technology, Volume 85(9), pp. 2857–2872
Zhao, N.Y., Lian, J.Y., Wang, P.F., Xu, Z.B., 2022. Recent progress
in minimizing the warpage and shrinkage deformations by the optimization of
process parameters in plastic injection molding: a review. The
International Journal of Advanced Manufacturing Technology, Volume
120, pp. 85–101
Zhou, J., Turng, L.S., Kramschuster, A., 2006. Single and
multi-objective optimization for injection molding using numerical simulation
with surrogate models and genetic algorithms. International Polymer
Processing, Volume 21(5), pp. 509–520
