Improving Salt Farmer’s Bargain Power through Demand Allocation and Profit Sharing: A Cooperative Game Approach
Corresponding email: budisantoso.wirjodirdjo@gmail.com
Published at : 25 Jan 2024
Volume : IJtech
Vol 15, No 1 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i1.5522
Maflahah, I., Wirjodirdjo, B.Karningsih, P.D., 2024. Improving Salt Farmer’s Bargain Power through Demand Allocation and Profit Sharing: A Cooperative Game Approach. International Journal of Technology. Volume 15(1), pp. 110-120
| Iffan Maflahah | 1. Department of Industrial and System Engineering, Faculty of Industrial Technology and System Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo, Surabaya 60111, Indonesia, 2. Dep |
| Budisantoso Wirjodirdjo | Department of Industrial and System Engineering, Faculty of Industrial Technology and System Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo, Surabaya 60111, Indonesia |
| Putu Dana Karningsih | Department of Industrial and System Engineering, Faculty of Industrial Technology and System Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo, Surabaya 60111, Indonesia |
Oligopoly has remained a
serious problematic market structure in the Indonesian salt supply chain, which
exterminates the bargaining power of farmers. To
eradicate the problem, a hybrid collaboration structures, i.e., vertical
collaboration (farmers with cooperatives) and horizontal collaboration (farmers
with farmers), are proposed, enabling to bring positive economic impacts to
farmers. This novel supply chain-system model follows the cooperative game
theory with Shapley's value for decision-making process. This work aimed to
evaluate the implementation of the two partnership models for the supply
chain of salt regarding their impacts on economic
benefits for farmers assessed by Shapley's value of
coalitions. The constructed model revealed that collaborative
works between salt stakeholders improved farmers’ revenue, and the optimum
benefit was achieved by farmers when their supply (?20%)
was purchased by cooperatives, while the remaining was bought by
middlemen. In this regard, the significant capacity of the
cooperative should be invigorated in various sectors, including saving and loan
services, market seekers, salt
price making, and improvement of salt quality.
Although farmers-to-farmers collaboration also bring mutual benefits,
additional attempts by cooperatives, especially for small farmers, can be
created to nurture a partnership between cooperatives and farmers, enabling
them to generate more benefits.
Cooperative game; Horizontal collaboration; Revenue; Shapley value; Vertical collaboration
Salt has become a pivotal food component for human consumption. In Indonesia, salt development is hindered by factors such as low salt quality, inadequate salt production, price uncertainty, and a complicated supply chain. The main problem of the Indonesian salt supply chain relates to inefficiency and imperfect competition market (oligopoly) (Mustofa et al., 2021). The form of the oligopoly market is likely to be dominated by one of the actors, namely middlemen. The middlemen act as collection agents, purchasers, intermediaries and retailers. Domination of the middlemen includes the ability to control the price and quality of the product (Biglaiser and Li, 2018). Farmers only act as price recipients (Chandra and Sao, 2020) because they have limited market price information, making it difficult to bargain with middlemen (Mustofa et al., 2021).
From 2016 to 2019, salt prices
ranged $0.01 to $0.06 per kilogram (Suhendi, Abdullah,
Shalihati, 2020).
Farmers should get at least $0.06 per
kilogram to cover production costs. The
government regulates prices, but it is ineffective due to the role of
intermediaries. In addition, the government needs to hold the number of salt
imports and supply chain systems by increasing productivity. This
effort is to increase income by improving the bargaining ability of farmers. The salt supply chain can be enhanced by involving
cooperatives to increase farmers' revenue (Mustofa
et al., 2021).
Research on the salt supply chain have been approached using qualitative and quantitative approaches such as margin share methods (Rinardi & Rochwulaningsih, 2017), SWOT analysis (Holis, Sayyidi, and Musoffan, 2019), system dynamics (Muhandhis et al., 2021), and SCOR approach (Purnanto, Suadi, and Ustadi, 2020). Unfortunately, those methods are unable to discuss a collaborative model of the salt supply system. This drawback can be solved by other approaches, such as game theory, which enables to overview of the collaborations aiming to increase farmer’s revenue. The method can formulate and analyze competitive situations and conflicts implicating more than one player with disparate goals (Maschler, Solan, and Zamir, 2013). Determination of options for the supply chain system for agricultural products (Prasad et al., 2019) and allocation of product supply (Bonamini et al., 2019) using the game theory. Game theory can be applied to agricultural products in various ways. For instance, it can use a single pricing strategy or a two-stage pricing strategy for products in the chain of two echelons - suppliers and retailers (Chen et al., 2018). Additionally, game theory can also be used to determine the coordination approach between farmers and traders while accounting for uncertainties like harvesting yields and demand (Behzadi et al., 2018; Gao, Yang, and Liu, 2017).
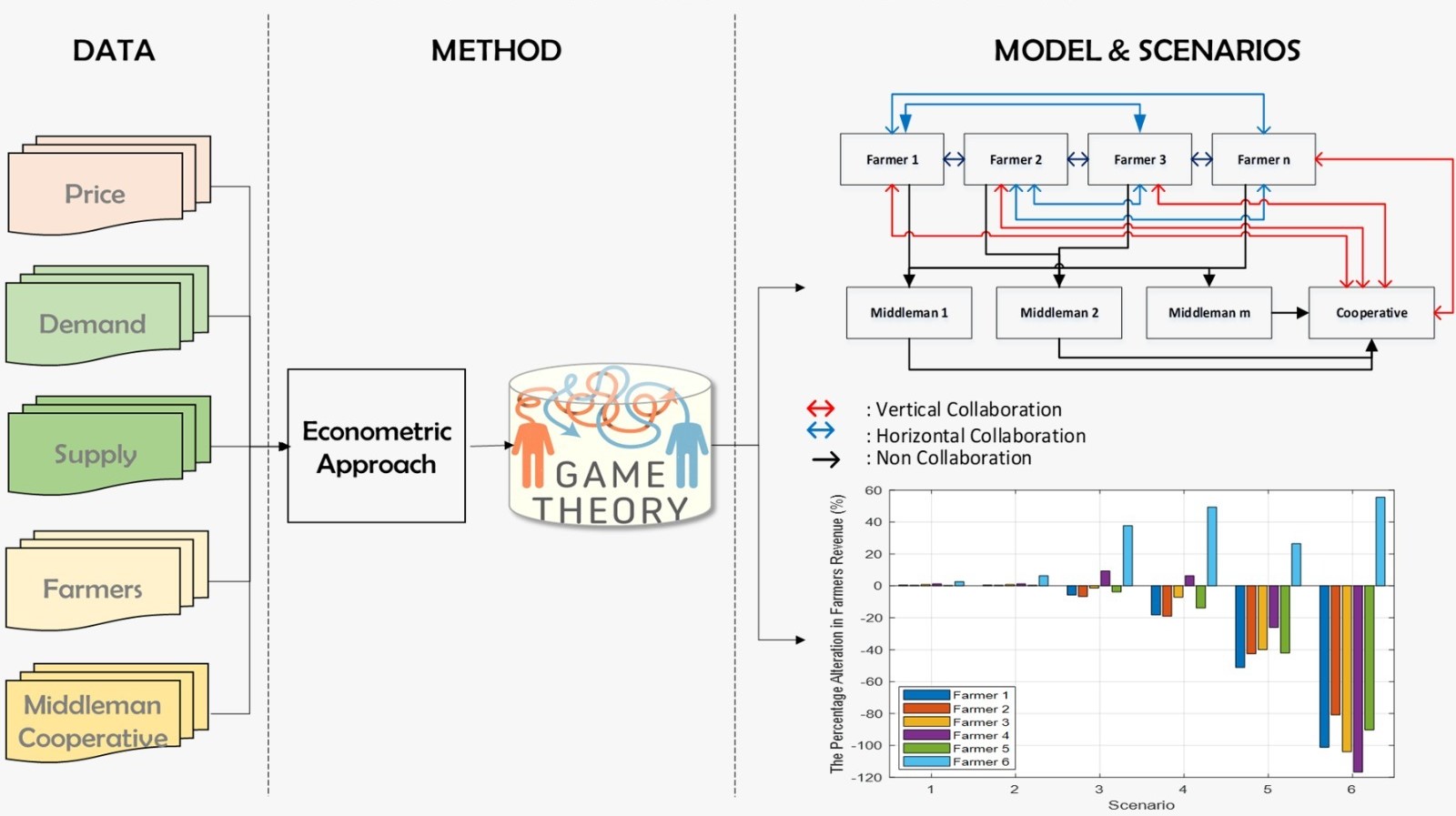
This study applies coalition game theory and transferable utility concepts using cooperative games. Coalition members are assumed to agree on the price and amount of payoff among the members (Maschler, Solan, and Zamir, 2013). The coalition in the salt supply-chain model involves a cooperative as one of the key elements in the system. In this regard, a cooperative has the functions of facilitating salt farmers to improve their revenue. Moreover, farmers, middlemen, and cooperatives have different interests. Implementing vertical (farmers with cooperative) and horizontal (farmers with farmers) collaboration systems is expected to improve the salt supply chain. Vertical collaboration is a partnership between farmers and cooperatives to reduce the role of the middlemen (Zhong et al., 2018). In addition, a horizontal collaboration between farmers and farmers is also able to increase revenue (Martins, Trienekens, and Omta, 2019). This work aimed to evaluate the implementation of horizontal and vertical collaboration models regarding their impacts on farmers' revenue based on the Shapley value obtained from the salt supply chain coalition.
1.1. Cooperative Game Theory
Shapley's value is used to determine the optimal
solution in cooperative game theory. Each
participant's final result in the game focuses on the
acquisition in the cooperative game. The
coalition is an agreement of the N player set based on the game's mathematical
model and is represented by the symbol S (Brown & Shoham, 2008). A grand coalition is an agreement of all players (n
players) without an empty coalition with a 2n possible alliance. The structure coalition is how the player forms a
coalition where a set of S = (S1, S2, ..., Sm) of the m coalition is built. Some definitions of the Shapley
value concept in cooperative game theory are as follows:
Definition 1 The
transferable utility used in coalition games (N,v) consists of: (1) a set of
N players; (2) the characteristic
function of the game v(S) is the total coalition available to all members of S
of N players, which N is the set for each player, for i = 1, 2, ..., n. 
The grand coalition is the N set and not the empty set 
for all S and T where 
The concept of cooperative games is a super
additive 
where the
acquisition of coalition results must be greater or equal to non-coalition
income (Brown & Shoham, 2008).
if xx is the xx carrier, then 
for each permutation 
; if u and v are two games: 
then Shapley's value 
with the number of players in the 
Each player has
2n-1 possible coalition forms. Player i revenue from a coalition
is called the payoff value, so the value of the player's contribution is 
i to the S coalition.
for each coalition S with i.
some of the axiom used are (1) symmetry: If i and j are exchangeable in 
dummy: If i is
a dummy player in 
and (3) additivity: If there are two games v and w, then, 
for every, 
where 
2.2. Model Formulation
Vertical and horizontal collaboration model is used to solve the salt supply chain problem. The stakeholders involved in this coalition are farmers, middlemen, and cooperatives (Figure 1). Farmers, as members, are obliged to sell a certain amount of salt through cooperatives.
Figure 1 The Salt Supply Chain Coalition Model
The research used six players (farmers
1, 2, 3, 4, 5, and 6). The characteristic function as
follows: 
The Shapley values were 
The Shapley value was determined
using a selling scenario in which salt was sold based on the farmer's minimum
obligation as cooperative members and the rest is sold through middlemen. As
cooperative members, farmers are required to sell salt for at least 10% of the
total production through the cooperative. The scenarios for selling salt from
farmers to middlemen 1, middlemen 2, middlemen 3 and cooperatives are: scenario
1 (30%, 40%, 20%, and 10%); scenario 2 (30%, 30%, 20%, and 20%); scenario 3
(25%, 25%, 25%, and 25%); Scenario 4 (40%, 20%, 10%, and 30%); Scenario 5 (10%,
30%, 20%, and 40%); and Scenario 6 (20%, 10%, 10%, and 60%).
2.3. Construction
of Shapley Value Salt Coalition Model
The model illustrates the average
contribution of six farmer coalition members {1, 2, 3, 4, 5, 6} in all possible
steps. Moreover, the player revenue is used for Shapley value calculations. The
salt supply chain channel will determine the amount of farmer revenue. Members of the salt supply chain are ith farmer (i=1,2, …,
n), jth middleman (j=1, 2. …, m), and kth cooperatives
(k=1, 2, …, h), while the salt supply and salt
price in the intermediary depend on tth time (t = 1.2,
..., l). In addition, the salt demand middlemen j at the time t (Dajt)
Middleman
revenue is obtained from the sale of salt by seeing the negotiation cost (Ca), and salt carrying capacity (G). The
formula of the middleman's revenue 
at time t
is shown in Equation 1.
The cooperative's revenue is revenue from procuring
salt from farmers i and benefits
distribution 
The membership fee of the cooperative is 
The formula of the cooperative revenue k at the time 
defined in Equation 2.
is the middlemen j revenue and cooperatives k
revenue. Farmer i must become delegates cooperatives to achieve a vertical
collaboration system. Furthermore, the supply farmer i through middlemen j at
time t (qajit), and cooperatives k at time t (qbkit) The cooperative and farmer I collaborates
have to bear half of the percent real risks 
the negotiation fee (C), the membership fee (Cmit), and receive a benefit distribution 
There are
three types of farmer’s revenue based on a horizontal collaboration, namely:
(i)
Farmers only
sell salt according to the supply produced 
The farmer's revenue is obtained from the salt supply through middlemen j and cooperativ
cooperative k, so the farmer i revenue at time t 
is explained in Equation 3.
(ii) The farmers who buy salt from other farmers
Farmers receive
revenue through middlemen j, and
cooperatives k, and part of the
profits are shared from cooperatives. However, farmers, i have to pay for a certain amount of salt purchased from other
farmers. Therefore, the formula of farmer i revenue at time
t 
defined
in Equation 4.
(iii) Farmers whose supply exceeds the demand of middlemen and cooperatives 
Farmers'
revenue is obtained from sales through middlemen, cooperatives, and coalitions
with other farmers, so the farmer income model is described in Equation 5.
In this scenario, all farmers (Farmer 1, Farmer 2, Farmer
3, Farmer 4, Farmer 5, and Farmer 6) are responsible for meeting the demands of
three middlemen (Middlemen 1, Middlemen 2, and Middlemen 3) and the
cooperative. The supply of salt from the farmers, as well as the demand from
the middlemen and the cooperative, varies for each time period. Additionally,
the prices offered to the farmers by each middleman and the cooperative also
differ. The salt price at the market in period t (Pmt) $83.22/tons; cooperative salt price k in period t (Pbkt) $76.28/tons; salt carrying capacity (G) 9
tons; risk of selling through cooperatives 
benefit distribution (cooperatives and
farmers) 
negotiation costs from pond to
cooperatives (C) $3.12/tons; salt negotiation costs by middlemen to the market
(Ca) $6.73/tons; negotiation fee from cooperative to market (Cb) $3.12/tons;
percentage drop in salt price (r) 40%; cooperative membership fee 
$2.08/period.
The salt supply chain system without a coalition is the
initial scenario in which farmers sell through middlemen 1, 2, and 3 (30%, 20%,
20%) and cooperatives (20%). Based on the scenario, the total revenue of farmer
is: farmer 1, farmer 2, farmer 3, farmer 4, farmer 5, and Farmer 6 ($18,079; $27,450;
$10,346; $5,703; $47,854; $2,532).
Horizontal collaborations are used as the basis for the
coalition game scenario. A coalition carried out by farmers is expected to
provide a minimum revenue equal to or greater than not conducting a
coalition. The coalition of six farmers
in each coalition formed the functional characteristics based on Definition
1 (Table 1). Shapley's
value is the solution problem states that the concept of a coalition forms a
grand coalition in each game (Brown
& Shoham, 2008).
Table 1 Farmer supply as a base, for example, Characteristics of the v(S) function
|
Number Coalition
Farmer |
Farmers
Revenue v(S)
($) |
Number Coalition
Farmer |
Farmers
Revenue v(S)
($) |
Number Coalition
Farmer |
Farmers
Revenue v(S)
($) |
|
1 |
18,079 |
3-2-1 |
55,848 |
5-3-2-1 |
103,760 |
|
2 |
27,450 |
4-2-1 |
51,193 |
5-4-2-1 |
99,104 |
|
3 |
10,346 |
4-3-1 |
34,038 |
5-4-3-1 |
81,949 |
|
4 |
5,703 |
4-3-2 |
43,438 |
5-4-3-2 |
91,349 |
|
5 |
47,854 |
5-2-1 |
93,470 |
6-3-2-1 |
58,302 |
|
6 |
2,532 |
5-3-1 |
76,315 |
6-4-2-1 |
53,647 |
|
6-5 |
50,435 |
4-3-2-1 |
61,482 |
6-5-4-3-2-1 |
111,848 |
Shapley value ($18,092.40; $27,486.39;
$10,355.17; $5,702.19; $47,940.93; $2,617.90)
The Shapley value obtained is the
average contribution of the farmer coalition {1,2,3,4,5,6}. When one of the
players performs an S coalition, then contribute to improving the game by as
much as 
. Farmer's contribution 6 to the grand
coalition {6,5,4,3,2,1} is only v ({6}) = v(6) = $2,532 . The number of grand
coalition combinations is 6! - 1 = 719, producing the same value. Suppose that
the grand coalition formed from the coalition {4,2,6,1,3,5} gives the same
result as the coalition {1,2,3,4,5,6}, which is $111,848. In the farmer
coalition {4,2,6,1,3,5}: revenue
contributions from farmers 1 ($18,079); farmer 2 ($27,450); farmer 3 ($10,346);
farmer 4 ($5,703); farmer 5 ($47,854); and farmer 6 ($2,532). While the contribution of farmers from the
coalition {1,2,3,4,5,6}, namely farmers 1 ($18,079.34), farmers 2 ($27,479),
farmers 3 ($10,289.68), farmers 4 ($5,634.29); farmer 5 ($47,376.24); and
farmer 6 ($2,989.68).
There are still 5! – 2 = 118 remaining
permutations in the Shapley value step present, and the results were averaged
for each farmer. Thus,
the imputation is as follows: 
Theorem
1: Table
1 shows the characteristic function that produces the
shapley value for farmers 1, 2, 3, 4, 5, and 6 as follows: $18,092.40; $27,486.39;
$10,355.17; $5,702.19; $47,940.93; and $2,617.90. Teorema Shapley
value (super additive) i.e. the revenue of each player with coalition
system must be greater than or equal to revenue non-coalition (Brown
& Shoham, 2008).
This is evidenced by the increase in farmers' incomes with the concept of a
coalition based on Shapley values of: 100.45%, 100,386%, 100.76%, 101.22%,
100.33%, and 106.29%.
Theorem 2: The
core of the cooperative game is Shapley values based on characteristic functions
(Table 1
).
Evidence: Based on Shapley's
value, the total revenue of coalition farmers 4-3 ($16,057.35), coalition
farmers 4-3-1 ($34,149.75), and coalition farmers 5-4-3-1 ($82,090.68). This
value is used to verify the revenue presented on Shapley's solution 
which is $18,092.40;
$27,486.39; $10,355.17; $5,702.19; $47,940.93; and $2,617.90.
The revenue
generated by the player is higher than the revenue determined by the
characteristic function (Table 1), and an example of a verified coalition is
{1, 3, 6}. The total revenue earned by this particular coalition, as determined
by Shapley's solution, is $31,065.47,
which is the sum of the revenues earned individually by players 1, 3, and 6: $18,092.40; $10,355.17; and $ 2,617.90,
respectively. Shapley's value solution
shows the total revenue of the farmer coalition {1,3.6} is $31,065.47. This value is smaller than the characteristic function
(Table 1) which is v {1, 3, 6} = $30,857.99. It is conformity Shapley's
value concept in Definition 1, which
indicates that v(S) is the maximum value guaranteed by the S coalition by
coordinating the strategies of its members regardless of the activities of
other players (Brown
& Shoham, 2008).
The revenue of each farmer based on the scenario is shown
in Figure 2.
Figure 2 Farmer`s revenue: (a) Scenario 1; (b)
Scenario 2; (c) Scenario 3; (d) Scenario 4; (e) Scenario 5; and (f) Scenario 6
Figure 3 shows the revenue of middlemen and cooperatives based on coalition and non-coalition models. In the vertical coalition model, farmers must contribute fees to cooperatives, but cooperatives must also provide profit sharing with farmers. In comparison, in the non-coalition model, farmers and cooperatives do not have obligations to each other.
Figure 3 Total Revenue: (a) Cooperative; and
(b) Middlemen
The
cooperative revenue increases when the cooperative implements a vertical
collaboration. Non-cooperative revenue is $367.55, cooperative revenue with a
coalition system increases to $ 479.88 (scenario 1); $ 1187.41 (scenario 4) and
continues to increase in line with the rise in the number of farmers buying
salt (Figure 3 a). The
increase in the cooperative's revenue is obtained from the value of member
contributions of $ 2.08 per period.
Figure
3 (b) shows
the revenue earned by the middlemen. The middleman's revenue is determined by
the amount of salt purchased from the farmer. The middlemen's revenue decreases
when farmers apply a coalition system in determining the channel of the salt
trade system. The income of middleman 1 decreased from $30,642.86 to $25,777.05
when the farmer sold 30% of his salt supply. Likewise, when farmers sell 25% of
the supply of salt to middlemen, the income of middleman 1 decreases to $10,315.19.
Figure
2 and Figure
3 (a)
represent the farmers and cooperative revenue. The total revenue of farmers
with the coalition system in scenarios 1 and 2 is higher than that of
non-coalition (Table 2). It is by
Shapley's concept of value in Definitions 1, 2, and 3, which states that
players' revenue is greater than or equal to the revenue of non-coalition.
|
|
Farmer
1 |
Farmer
2 |
Farmer
3 |
Farmer
4 |
Farmer
5 |
Farmer
6 |
|
Scenario 1 |
79.56 |
91.25 |
70.41 |
65.84 |
116.66 |
63.30 |
|
Scenario 2 |
82.41 |
105.78 |
78.47 |
68.81 |
156.10 |
154.90 |
Farmers get different revenue
when selling salt with a coalition system. Horizontal and vertical
collaboration is essential for farmers because farmers get information on
prices and the use of resources together (Martins,
Trienekens, and Omta, 2019).
The price information is vital to influence farmers' choice of supply chain
channels. The maximum revenue of farmers based on the salt supply-chain
coalition system is scenario 2. When farmers sell through cooperatives more
than 20% of the salt supply, the farmers will experience losses. The decrease
in farmer’s revenue results from the significant rise in transaction costs.
However, farmers are very dependent on middlemen, especially on providing cash
and the payment system after harvest (Chandra
& Sao, 2020).
The banking system and cooperatives cannot do this. Farmers prefer to work with
middlemen because farmers get a net income without thinking about the market.
Likewise, salt farmers choose to sell salt through middlemen because the farmer
sell their salt on the pond, and middlemen carry out the post-harvest
processing (Mustofa
et al., 2021; Sasongko et al., 2019).
The biggest challenge is finding a market when the harvest season occurs (Kontogeorgos
et al., 2018).
Due to a lack of access, salt farmers prefer to sell their salt to middlemen
rather than send it directly to the company. On the other hand, the company
only accepts salt from suppliers in partnership. To cope with this problem, a
collaboration between farmers and cooperatives can be a promising strategy.
Long-time partnerships between the cooperative and the company allow ensuring
salt market certainty.
The role of cooperatives for farmers is
to increase the revenue of their members. In addition, the collaboration of
farmers and cooperatives can accommodate the products produced by farmers (Ma
and Abdulai, 2016).
Figure
2 shows
farmers' revenue increase with the coalition supply chain system. However,
farmers must become cooperative members in this supply chain system to benefit.
Cooperatives can buy products from members and non-members, but the value of
the profits obtained is different (Wicaksono,
Arshad,
and Sihombing, 2019).
Another advantage obtained is that farmers do not have to look for market
share, bear transaction costs, and protect products from market uncertainty (Alho, 2015).
As members of the cooperative, farmers will receive training to improve product
quality according to market demand. Product acceptance in the market and
supplier selection depend on several variables, namely quality, price,
marketing period, delivery time, and service (Al-Hazza
et al., 2022; Setyaningrum, Subagyo, and Wijaya,
2020).
In this case, salt acceptance relies on the following requirements, i.e., salt
quality, supply stability, and price. Salt price often positively relates to
salt quality. Therefore, the use of advanced salt production technologies can
raise salt quality (Amir
et al., 2021),
which in turn, leads to improved farmer revenue.
The current research is one of the studies to decide the
utility of any element of the salt supply chain with different levels of
importance. It only involves farmers, middlemen, and cooperatives as the salt
supply chain elements. Based on the Shapley value obtained, the horizontal and
vertical collaboration system can increase farmers' revenue, namely maximum
sales through cooperatives, 20% of the salt supply produced. Cooperatives can
increase farmers' revenue by improving services and reducing transaction costs.
This research does not consider the traditional relationships between middlemen
and farmers, including transaction (payment) methods between them. In addition,
the proposed model is developed as a representation of a one supply chain
system that consists of farmers and middlemen, whereas the supply chain between
farmers to salt processing factories is not included. Further research is
necessary to design other forms of partnership and rewards aiming to reveal the growing profitability due to
partnerships between farmers and cooperatives. Models can be made
through different commissions according to the amount of salt sold and
different prices according to the quality of the salt produced.
Al-Hazza, M.H., Abdelwahed, A., Ali, M.Y.,
Sidek, A.B.A., 2022. An Integrated Approach for Supplier Evaluation and
Selection using the Delphi Method and Analytic Hierarchy Process (AHP): A New
Framework. International Journal of Technology, Volume 13(1), pp. 16–25
Alho, E., 2015. Farmers’ Self-Reported Value
of Cooperative Membership: Evidence from Heterogeneous Business and
Organization Structures. Agricultural and Food Economics, Volume 3(1),
p. 23
Amir, N., Efendy, M., Yoo, Y.J.,
Gozan, M., 2021. Improved Salt Quality and Reduced Energy Consumption via Hot
Air Drying. International Journal of Technology, Volume 12(3), pp. 592–601
Behzadi, G.,
O’Sullivan, M.J., Olsen, T.L., Zhang, A., 2018. Agribusiness Supply Chain Risk
Management: A Review of Quantitative Decision Models. Omega, Volume 79,
pp. 21–42
Biglaiser, G., Li, F., 2018. Middlemen: The
Good, The Bad, and The Ugly. The RAND Journal of Economics, Volume
49(1), pp. 3–22
Bonamini, G., Colombo, E., Llorca, N.,
Sanchez-Soriano, J., 2019. Cost Allocation for Rural Electrification Using Game
Theory: A Case of Distributed Generation in Rural India. Energy for
Sustainable Development, Volume 50, pp. 139–152
Brown, K.L., Shoham, Y., 2008. Essentials
of Game Theory. California, USA: Morgan & Claypool Publisher
Chandra, Y.,
Sao, P., 2020. Case Study on Salt Farmers: A Sustainable Livelihood
Approach. Indian Journal of Social Work, Volume 81(1), pp. 119–134
Chen, X., Wu, S., Wang, X., Li, D., 2018.
Optimal Pricing Strategy for The Perishable Food Supply Chain. International
Journal of Production Research, Volume 57(9), pp. 2755–2768
Gao, J., Yang, X., Liu, D., 2017. Uncertain
Shapley Value of Coalitional Game with Application To Supply Chain Alliance.
Applied Soft Computing Journal, Volume 56, pp. 551–556
Hao, J., Bijman, J., Gardebroek, C., Heerink,
N., Heijman, W., Huo, X., 2018. Cooperative Membership and Farmers’ Choice of
Marketing Channels – Evidence from Apple Farmers in Shaanxi and Shandong
Provinces, China. Food Policy, Volume 74, pp. 53–64
Holis, M., Sayyidi, S., Musoffan, M., 2019.
Optimization Analysis of Salt Farmers Activities and Welfare in Pamekasan
Regency. EAJ (Economics and Accounting Journal), Volume 2(3), p. 198
Kontogeorgos, A.,
Sergaki, P., Kosma, A., Semou, V., 2018. Organizational Models for
Agricultural Cooperatives: Empirical Evidence for their Performance. Journal
of the Knowledge Economy, Volume 9(4), pp. 1123–1137
Ma, W., Abdulai, A., 2016. Does Cooperative
Membership Improve Household Welfare? Evidence from apple farmers in China. Food
Policy, Volume 58, pp. 94–102
Martins, F.M., Trienekens, J., Omta, O.,
2019. Implications Of Horizontal and Vertical Relationships on Farmers
Performance in The Brazilian Pork Industry. Livestock Science, Volume
228, pp. 161–169
Maschler, M., Solan, E., Zamir, S., 2013.
Game Theory. Cambridge: Cambridge University Press
Muhandhis, I., Wirjodirdjo, B., Suryani, E.,
Susanto, H., Asfari, U., 2021. Modeling of Salt Supply Chains to Achieve
Competitive Salt Prices. International Journal on Food System Dynamics,
Volume 12(1), pp. 51–67
Mustofa, M.,
Komariyah, S., Yuliati, L., Supeni, N.,
2021. Development
Strategy for Salt Farmers Market Access in East Java Indonesia: SWOT Analysis
Approach. International Journal of Social and Administrative Sciences, Volume
6(1), pp. 8–13
Prasad, S., Shankar,
R., Roy, S., 2019. Impact of Bargaining Power on Supply Chain Profit
Allocation: A Game-Theoretic Study. Journal of Advances in Management
Research, Volume 16(3), pp. 398–416
Purnanto, S.H., Suadi, S., Ustadi, U., 2020. Salt Supply Chain Management at
Regional Level: Case Study of Salt Processing Industry and Salt Consumer
Industry in Central Java. Jurnal Perikanan Universitas Gadjah Mada,
Volume 22(1), pp. 63–70
Rinardi, H., Rochwulaningsih, Y., 2017. Salt
Cooperatives as Public Credit Institutions for Coastal Communities: A Case
Study of Two Salt Cooperatives in Rembang and Demak. Journal of Maritime
Studies and National Integration, Volume 1(1), pp. 66–77
Sasongko, B., Elfindri, E., Sjafrizal, Husni,
T., Satrianto, A., 2019. Production Optimalization Analysis and Maximization
Profit of Salt Farmers on the Madura Island. In: Proceedings of the 5th
Annual International Conference on Accounting Research (AICAR 2018), pp.
134–138
Setyaningrum, R., Subagyo, Wijaya, A.R.,
2020. A Mathematical Model of Factors Driving Product Success in an Indonesian
Market using Design of Experiment. International Journal of Technology,
Volume 11(2), pp. 322–332
Suhendi, Abdullah,
A., Shalihati, F., 2020. The Effectiveness of The Salt Policy in
Indonesia. Jurnal Manajemen dan Agribisnis, Volume 17(3), pp. 315–324
Wicaksono, F.D., Arshad, Y.B., Sihombing, H.,
2019. Monte Carlo Net Present Value for Techno-Economic Analysis of Oil and Gas
Production Sharing Contract. International Journal of Technology, Volume
10(4), pp. 829–840
Zhong, Z., Zhang, C., Jia, F., Bijman, J.,
2018. Vertical Coordination and Cooperative Member Benefits: Case Studies of
Four Dairy Farmers’ Cooperatives in China. Journal of Cleaner Production,
Volume 172, pp. 2266–2277