Enhancing A Reliable Ship Performance Evaluation in Dynamic Maneuvering Conditions – A Gap Analysis
Corresponding email: sunarsihits@gmail.com
Published at : 09 May 2023
Volume : IJtech
Vol 14, No 3 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i3.5489
Sunarsih, Jadmiko, E., Zaman, M.B., Malik, A.M.A., Ali, A., 2023. Enhancing A Reliable Ship Performance Evaluation in Dynamic Maneuvering Conditions – A Gap Analysis. International Journal of Technology. Volume 14(3), pp. 561-575
| Sunarsih | Department of Marine Engineering, Faculty of Marine Technology, Institut Teknologi Sepuluh Nopember, Surabaya 60111, Indonesia |
| Edi Jadmiko | Department of Marine Engineering, Faculty of Marine Technology, Institut Teknologi Sepuluh Nopember, Surabaya 60111, Indonesia |
| Muhammad Badrus Zaman | Department of Marine Engineering, Faculty of Marine Technology, Institut Teknologi Sepuluh Nopember, Surabaya 60111, Indonesia |
| Adi Maimun Abdul Malik | Marine Technology Centre, Universiti Teknologi Malaysia, 81310 Skudai, Johor Bahru, Malaysia |
| Arifah Ali | Department of Aeronautical, Automotive and Offshore Engineering, School of Mechanical Engineering, Universiti Teknologi Malaysia, 81310 Skudai, Johor Bahru, Malaysia |
Ship and propeller interaction greatly affect ship
maneuvering performance and behavior. In steady ahead operation, the
interaction properties remain unchanged due to steady ship-propeller
operations. In dynamic operations, such as stopping, the properties vary
considerably based on the ship and propeller speed combinations. Past
researches and practices use a simplistic assumption of single and constant
value resembling steady ahead operation due to the lack of knowledge and data
on the properties. Up to very recently, researchers in the field and related
areas refer to the one and only work from more than five decades ago. The
current research presents an insight to disclose the properties features,
efforts, and progressions made in the field to the extent of challenges
bottlenecking the development. The work broadens the analysis of the
implication and inadequacy of the current circumstance toward appropriateness,
accuracy, and validity of the research and related studies in the field.?
Crash stopping; Dynamic operation; Hull-propeller interaction; IMO maneuvering; Propulsion factor
The quality of ship maneuvering is exceptionally
important from both technical and operational points of view. Ship
maneuverability is of great interest to ship owners, operators, ports, and
state authorities. In addition to collision avoidance, ship maneuverability
should be prioritized in further studies due to the criticalness and impact on
ship safety and operability (Vanem et al., 2008). From
a practical point of view, there is an evolution of needs from day-to-day
operations involving ship maneuverability to computer-aided simulation modeling
(Cimen, 2009; Pérez and Clemente, 2007; Benvenuto, Brizzolara, and Figari,
2001) under
various operating conditions (Paroka, Muhammad, and Asri, 2017;
Prabowo et al., 2016; Priadi and Tjahjono, 2015). The
method which averts the necessity of conducting costly and
time-consuming full-scale trials and allows a wider range of operations without
jeopardizing the ship, such as in the case of crash-stopping maneuver, is the
most promising tool to investigate and assess the ship maneuvering behavior and
maneuverability compliance to IMO Manoeuvring Standards (IMO, 2002b). However, an appropriate mathematical
model and precise knowledge of various coefficients used in the modeling are
required to produce accurate and satisfactory results (Cimen,
2009).
In contrast to the inherent design and
most of the daily operations in forward movement indicating ahead operation,
dynamic ship maneuvering such as during crash stopping requires propeller
function in four-quadrant operation comprising ahead, crash-ahead, crash-back,
and backing. Unlike traditional maneuvering modeling, the mathematical model
and coefficients employed in such dynamic operation hence demand to be in the
similar mode of four quadrant operation. To be precise, realistic knowledge of
various ship hull and propeller interactions represented by wake and thrust
deduction fractions is indispensable for satisfactory maneuvering prediction (Voorde,
1974). However, knowledge and data on the
hull-propeller interaction properties in various maneuvering conditions are
very limited (Ye
et al., 2012; Sutulo and Soares, 2011; Artyszuk, 2003; Harvald, 1976). The work
of Harvald
(1977, 1967) as the pioneer (Artyszuk,
2003) since more than a half-century
ago is still referred to by various researchers in the field and related areas
up to now (Illes et
al., 2021, 2020; Sunarsih, 2018; Trodden and Haroutunian, 2018; Sutulo and
Soares, 2011). Only recently, Sunarsih
(2018) was recorded to execute similar
research and took advantage of the properties developed to evaluate
ship-stopping ability based on the Standards framework.
Reference of nowadays researches to
outdated works, such as Harvald (1977, 1967), due to the
absence of further studies afterward bearing the consequence that there is an
enormous knowledge gap in the field and the current situation remains the same
as decades ago. Despite the fact and the urgency to take any proper actions, no
investigation has been performed to unveil the core and the aftermath problems.
Addressing the issue, this paper carried out an in-depth analysis to expose the
challenges in the advancement by profoundly observing related research thus far
and rooted the analysis to the pioneering work. Implications of the existing
limitations were outlined accordingly to encourage further studies in the field
and related areas.
The current research carried out a systematic review to identify the knowledge gap in the field of dynamic maneuvering involves various hull-propeller interactions indicated by various wake and thrust deduction fractions based on Artyszuk’s claim (Artyszuk, 2003) that Harvald (1977, 1967) is the pioneering work and solid evidence declared by Sunarsih (2018) that nothing has been progressed afterward up to years ago. Figure 1 illustrates the research framework employed as the basis of the systematic review performed.
Figure 1
Evidence-based framework for a systematic review of the current research
As evidenced, the work of Harvald
(1977, 1967) was referred to by Trodden
and Haroutunian (2018) who studied
the sensitivity of ship maneuvering motion on NOx formation years ago for further reference and
analysis. Formerly, Sutulo
and Soares (2011) who
reviewed various selected topics related to mathematical models mainly for
simulation of ship maneuvering purposes acknowledged that not much data on the
properties were available aside from the work hence encouraging the collection
of new data. Recently, both Illes
et al. (2021) and
Illes
et al. (2020) also
listed the work despite unclear contributions to the studies.
The research recalled the pioneering
work of Harvald
(1977, 1967) and
associated researches dealing with the development, modeling, and application
of the properties towards knowledge advancement and development of reliable
maneuvering prediction in dynamic operating conditions. Four key points set as
structured issues to develop an insightful analysis and gain the knowledge
about the topic are defined based on the following research questions: What has
been investigated in the past? What advancement has taken place? What
bottlenecks the development? And; what does the limitation suggest?
The outcomes
of the in-depth analysis of the four key points set for the systematic review
performed were outlined as follows.
3.1. Pioneer Studies in the Field
Records have shown that pioneer studies of various propulsion factors of wake and thrust deduction fractions implying dynamic maneuvering are dominated by experimental-based works. As seen in Figure 2, some studies were purposely carried out to identify the properties while others defined the properties through investigation of the involved test parameters throughout dynamic maneuvering.
Figure 2
Experimental-based studies in the field of dynamic propulsion factors
As the pioneer of the work, Harvald (1967) was recorded to identify various propulsion factors
of wake and thrust deduction fraction properties via overload tests of a
fishing trawler and bulk carrier models at several different speeds and propeller
revolutions in four quadrant operation. The models correspond to full-scale
ships of about 59,450 t and 60,000 t DWT, respectively. For
variation, the trawler model was tested using two different propellers while
the bulk carrier model was examined in combination with four blades fixed pitch
propeller. In the
work, the wake and thrust deduction values were determined
from the test data of thrust coefficient KT
in open water and behind ship conditions by performing
point-by-point calculations using both thrust and torque identities. The values
were then presented as functions of apparent advance coefficient J’.
A
decade later, investigation on the bulk carrier model was extended to operation
in infinite and restricted water depth conditions (Harvald, 1977). Two water depths of 1.5 and 1.25 times draft
of the model were selected to represent shallow water operation with the
distribution of ship speeds and propeller revolutions varied in three and four
settings ranges from 1.0 m/s to 1.8 m/s and 3 rps to 12 rps respectively for
both ahead and astern operations. Analyses of the test results for the
determination of wake and thrust deduction values and ship-stopping ability
were carried out as in previous research.
Despite
the fact of being the pioneering work in the field, the early work of Harvald (1967) was not mentioned in later works by Voorde (1974) and Tani (1968). It is uncertain whether both researchers
deserted the work or not knowing that such a study once was performed and
generated some properties. Unknowingly forsaking the established properties, Tani (1968) who investigated the stopping ability of
supertankers straightforwardly declared that no thrust deduction data for
stopping maneuvers exist at the time and the knowledge hence must depend upon
further study. During the analysis, the properties were assumed to be
neglectable despite some attempts to establish a simple calculation method
while preparing a set of calculation diagrams for the targeted ship.
In
the case of Voorde (1974), the work proclaimed that there was limited
knowledge and data regarding wake and thrust deduction properties in various
conditions during a stopping maneuver and related studies typically took the
values as constant. The study carried out an experimental test of stopping
maneuvers employing a high-speed cargo fitted with a controllable pitch
propeller. During the stopping test, propeller thrust T and ship speed u were
measured on a time basis.
In various attempts to model the dynamic thrust deduction
properties using the measured data, Voorde (1974) solved the longitudinal equation of motion
at the speed u expressed by Equation
1 where inputs are the measured thrust and ship speed,
and plotted
the thrust deduction values of (1-t)
as functions of thrust loading
However, Voorde (1974) encountered
difficulties in plotting the properties against the thrust coefficient CT and parameter u/nD
for constant pitch angles. The work denoted that it seems to be impossible to
present the properties as functions of propeller parameters due to too much
data scattering and uncertainties of the properties' behavior as redrawn in Figure 3. It
was believed that the problem was rooted in inaccuracies of both test data
comprising propeller thrust and ship speed, and mathematical computation in the
process of differentiation. The work indeed acknowledged that the thrust
measurements were not very accurate and justified that the model tests
performed were intended to develop a new technique for stopping tests in a
towing tank.
Later, Nakato et al.
(1976) carried out experimental
tests employing tanker and container models respectively identified as Ship T
and Ship C to estimate accelerating and decelerating ship motions. Differently,
the work acknowledged the thrust deduction properties established by Harvald (1967) and confirmed that propeller operation affects ship
accelerating and decelerating motions. The tests carried out revealed that
propeller thrust and its deduction factor which was almost independent of the
ship’s acceleration and deceleration were affected by the apparent advance
ratio Js (or J’,Jv = Vs/nD). Figure 4 depicts the thrust deduction properties (1–t)
identified for both ship models.
Based
on the finding, the work correspondingly regarded both the thrust and the
deduction factor as a function of the ship’s speed Vs and propeller revolution n. The work further determined the ship accelerating and
decelerating motions
3.2. Progression
in the Field and Related Areas
Research associated with various wake and thrust
deduction fractions representing dynamic maneuvering is not limited to
crash-stop modeling and analysis. As evidenced, research interest has emerged
in related areas such as thrust generation modeling and green shipping
involving such maneuvering conditions. Figure 5 chronologically captures past
research progressing the four quadrant wake and thrust deduction fraction
properties and modeling rooted in the work of Harvald (1977, 1967).
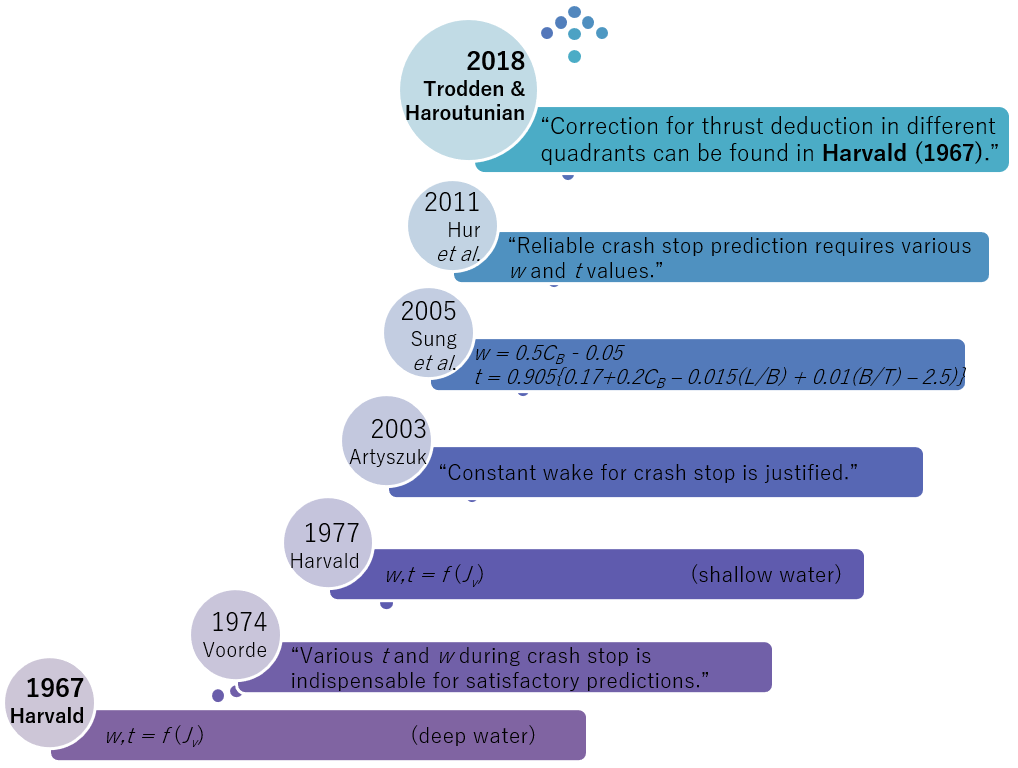
Harvald (1967) led studies in the field by carrying out overload tests in four-quadrant operations to identify various wake and thrust deduction values. Two ship models of a fishing trawler and a bulk carrier were employed in the tests. The test results including the wake and thrust deduction properties obtained were modeled and presented as maneuver nomograms depicting ship, machinery, and propeller interactions. Further, Harvald (1976) took advantage of the results and properties to analyze the sensitivity of various ship and propeller parameters to ship-stopping ability from a hydrodynamics point of view. Finally, the establishment of the wake and thrust deduction properties was continued to shallow water operation using the bulk carrier model (Harvald, 1977) where test results were analyzed and shown in the similar way.
Figure 5
Past studies on various hull-propeller interactions for dynamic maneuvering
Early research progressing
various wake and thrust deduction fractions properties in dynamic maneuvering
was recorded by Voorde (1974). The study which assessed ship-stopping behavior and
hull-propeller-interaction properties throughout the maneuver based on
measurement data revealed that data and knowledge pertaining to the properties
during crash stopping were scarce and difficult to obtain without even
considering the work of Harvald (1967) previously. However, agreement with such postulation was still found in
many later studies up to nowadays (Sunarsih, 2018; Sutulo and Soares, 2015; Artyszuk, 2011; Sutulo and Soares, 2011; Sung and Rhee, 2005, Artyszuk, 2003).
In contrast to
Artyszuk (2003), Voorde (1974) who analyzed the sensitivity of ship-stopping maneuver and steady-state
astern movement on the coefficients, Sutulo and Soares (2011) who reviewed various mathematical models mainly for simulation of ship
maneuvering then developed one, (Sutulo and Soares, 2015) acknowledged the properties of Harvald (1977, 1967) and irregularities in the behavior. Despite the values, Artyszuk (2003) declared that assuming the wake fraction for the prediction of
crash-stopping maneuver as a constant is justified whereas Sutulo and Soares (2011) disclosed that the fraction is typically estimated using simple empiric
formulae. In later reports, Artyszuk
(2011) and Sung
and Rhee (2005)
who developed generic
methods for the evaluation of ship-stopping ability took different approaches
to treat the properties. The earlier employed wake and thrust deduction values
estimated based on ship particulars as widely applied during the preliminary
design stage whilst the latter defined constant values for any maneuvering
conditions. As evidenced, discrepancies in
handling the properties were existed. However, Hur,
Lee, and Chang (2011)
and Voorde
(1974)
who analyzed propeller loads during crash-stop maneuvering emphasized that
reliable predictions in dynamic conditions during crash-stopping maneuver
require various values whilst simplistic assumptions of constant values
throughout any manoeuvring conditions, despite justifiable due to the lack of data and nothing better
is known, led to large errors in the predictions.
A relatively good
alternative approach in taking various wake and thrust deduction fractions into
account for dynamic maneuvering was presented by Ye
et al. (2012) who
developed a thrust estimation scheme for various ship operating conditions. The
work assumed the fractions to vary in values based on ship speed and propeller
RPM combinations. A better approach was shown by Ueno,
Suzuki, and Tsukada (2017) who
performed an estimation of full-scale ship-stopping ability using a
free-running model. The work assumed wake fraction (1–w) as a function
of maneuvering motion represented by -xP’r(L/V) whilst thrust deduction fraction treated as
a whole factor of propeller properties (1–t)KT assumed
as a function of advance ratio J. In contrast to both works, a recent study by Cui, Wu, and Chen (2018) who developed a simulation program for the evaluation of ship
maneuverability seemed to be neglectful of this issue. Nothing was disclosed
concerning dynamic wake and thrust deduction fractions despite the prediction
of crash-stopping ability performed.
3.3. Challenges in the Progression
Fundamentally, limited knowledge of some research areas was due to no continuation nor further research in the
field. Concerning the four quadrant wake and thrust deduction fractions, the
one and only work referred to nowadays research is the results of model tests by Harvald
(1977, 1967)
from decades ago. Albeit could not be assumed as completely true, the phenomenon could be read as negligence of
responsibility towards science society since emphases on
the exigencies of the properties and invaluable consequences for taking invalid
and inaccurate approaches in handling the properties have been simultaneously
proclaimed by past studies.
Harvald
(1977, 1967), Voorde
(1974)
and Tani
(1968)
have called for new property development. However, no significant progression
in the field appeared thereafter. The very recent work of Trodden
and Haroutunian (2018)
who studied the sensitivity of ship maneuvering motion on NOx formation still highlights the work of Harvald
(1967) for
the correction of thrust deduction fraction in various quadrants. Evidently,
knowledge and data of various wake and thrust deduction fractions nowadays are
still scarce and remain the same as those of more than five decades ago.
Considering the circumstances, the problem in aggregating
new and more data and knowledge on the properties might lie in the following three facts. Firstly, ships are
basically designed to move in one, forward direction at a specific design
speed. Correspondingly, treating the wake and thrust deduction fractions
representing the hull-propeller interaction in a similar way to only one ahead
operation might seem reasonable. Secondly, derivations and investigations of
the properties in four-quadrant operation either via experimental tests,
mathematical modeling, or numerical analyses are laborious, costly, and
time-consuming thus burdensome to be executed. Thirdly, it was widely known to
researchers in the field that simplistic postulations and practices to handle
the data and knowledge limitations on the properties were considered
justifiable. Hence, simply following such consent could be regarded as
acceptable.
According to Voorde
(1974),
various wake and thrust deduction fraction properties are derivable only by extensive tank tests of a fully fitted ship
model at overload conditions. It refers to propulsion tests at extremely high
propeller loadings hence enabling the model to create negative towing forces F and being self-propelled at particular
thrust values (MARIN, 1996). Indeed, laborious works were indicated by Harvald
(1967)
where in some cases tests were executed at lower than the desired speed whilst
some others were left out due to time consideration.
Artyszuk
(2003)
denoted that a more accurate relationship of the wake and thrust deduction
factors to propeller thrust and torque could be drawn by utilizing onboard
propeller measurement. However, propeller operation at extremely high loadings
could possibly jeopardize the ship and its related systems. While the
computation method could be set as an alternative to extensive tank tests which
are laborious, costly, and
time-consuming, Hur,
Lee, and Chang (2011)
disclosed that the cost of investigation of hydrodynamic loads involving
various operating conditions during crash stop operation accurately was also
considerably expensive. As a matter of fact, research cost has always been the
dominant factor bottlenecking further research for the cultivation of novel and
deeper knowledge in the field.
3.4. Implications
of the Current Status
As proven, knowledge and data of various wake and thrust
deduction fractions in four-quadrant operations representing various
maneuvering conditions are scarce and hard to find in previous works. Past to
current research made various assumptions in values and mathematical models of
the properties with justifications to treat the limitation while trying to
create better results. However, the accumulation of new properties and
modification of related mathematical models are significantly required since
invalid assumptions and improper mathematical modeling of the properties
bottleneck the realization of accurate hence reliable, and satisfactory ship
performance evaluation in dynamic maneuvering conditions.
3.4.1. Invalid
practices in handling knowledge and data limitation
As a result of limited knowledge and data of various wake
and thrust deduction fractions, studies concerning maneuvering in various and
dynamic operating conditions such as stopping-maneuvers assumed the properties
variously. The postulations take the form of certain values constantly, zero,
or as a function of certain parameters to the extent of neglectable. Artyszuk (2003), Harvald (1976), and Voorde (1974),
confirmed that the most common and thus simplest practices are assuming the
properties as a single value and remaining constant throughout any maneuvering
conditions. Voorde (1974) supposed such assumptions were
due to no better knowledge which was proven by Tani (1968)
who proclaimed that the data were unavailable at the time and hence neglected
during his assessment of large tanker stopping ability. Due to failure in
expressing the thrust deduction properties as function of propeller parameters,
Voorde (1974) then took constant thrust
deduction factor value (1-t) by 0.824
for estimation of the model ship stopping ability.
Among other past studies employing single and constant
wake and thrust deduction values were Cui, Wu, and Chen
(2018), Sutulo and Soares
(2015), Artyszuk (2011), Sung and Rhee (2005), Benvenuto, Brizzolara,
and Figari (2001).
For the mathematical model of ship standard maneuvers including crash stopping,
Benvenuto Brizzolara,
and Figari (2001) suggested the propulsion factors
of wake and thrust deduction to be estimated from the Holtrop method (Holtrop, 1984;
Holtrop and Mennen, 1982)
as formulated in Equation 4 and Equation 5 respectively if no tank test result
available.
Sung and Rhee (2005)
who proposed a new prediction method for ship stopping ability of diesel ships
fitted with FPP employed constant wake and thrust deduction fractions based on Taylor (1910)
as expressed in Equation 6 and Hideo and Oh (1971)
formula given by
Artyszuk (2011)
who previously proposed the determination of various thrust deduction fractions as
a function of maneuvering time while assuming the wake fraction as constant (Artyszuk, 2003)
employed default constant wake and thrust deduction fraction values
respectively by 0.3 and 0.15 to evaluate propulsive and stopping performance of
cellular container carriers.
Zero
propulsion factors (w,t = 0) which according to Harvald (1976)
were also frequently used in some studies were partially applied by Sunarsih, Izzuddin,
and Priyanto (2015) and Ye et al.
(2012). Both
works assumed the wake fraction as a function of the ship’s speed Vs while the thrust deduction
fraction was the function of propeller loading n, although constant values were given for both properties as
accordingly listed in Equation 7 and Equation 8. In the equation, Vse and ne correspond to ship-rated speed and engine rotational
speed.
As
propulsion factors of wake and thrust deduction fractions denote the ship and
propeller interactions, employment of constant values for one or both fractions
indicates that there is no change in the interaction which implies that the
ship and propeller operate at a specific speed and RPM combination constantly.
Meanwhile, the use of zero value signifies the absence of the ship and
propeller interaction. Definitely, the assumption and use of constant and zero
wake and thrust deduction values for four quadrant ship maneuvering modeling
are invalid since the values fail to account for the dynamic behavior of ship and
propeller interactions at various operating conditions involving various ship
speed and propeller rotational rate combinations which vary considerably
particularly during transition operation in crash stop maneuver (Sunarsih, 2018).
The
use of wake and thrust deduction fractions determined based on ship parameters
as executed by Sung and Rhee (2005)
and Benvenuto,
Brizzolara, and Figari (2001) are
also invalid since such expressions are usually derived from various model
tests as typical values and generally applicable for design condition hence for
a particular ship design speed and propeller rotational rate only. In fact,
according to Lewis (1988),
wake and thrust deduction fractions proposed by Holtrop (Holtrop, 1984; Holtrop
and Mennen, 1982)
which were used by Benvenuto Brizzolara,
and Figari (2001)
were derived from more than 200 model propulsion tests vary in types
statistically. Furthermore, as ship design is by default considers ahead
operation only, taking such typical values/expressions for four quadrant ship
maneuvering mathematical modeling includes crash stopping operation as in Cui, Wu, and Chen
(2018), Oneto et al.
(2018), and
Sutulo and Soares
(2015),
are considered as an invalid approach.
3.4.2. Improper modeling of dynamic
hull-propeller interaction
Several efforts toward modeling various wake and thrust
deduction fraction properties representing dynamic hull-propeller interaction
and taking them into account in four quadrant ship maneuvering mathematical
modeling, particularly for evaluation of ship-stopping ability have been
devoted to previous research. The attempts were mainly based on experimental
test results from overload tests to the extent of free-running and stopping
tests. Most approaches in the modeling were done by employing propeller-based
parameters including propeller loading and advance ratio.
As
dynamic ship maneuvering in four-quadrant operation involves various ship
speeds and propeller rotational rates, the most suitable parameter to represent
both variables is the apparent advance ratio Jv (
In
the work of Voorde (1974),
it was stated that both wake and thrust deduction fractions are primarily
dependent on the ship geometry mainly of the after body, propeller arrangement,
loading condition, and so forth. The work further denoted that it seems
acceptable to assume both fractions only as functions of the ship speed and
propeller thrust magnitudes while independent of the ship speed and propeller
loading combinations the thrust achieved. Such a presumption has been proven to
be erroneous based on the findings of Harvald (1977, 1967)
and experience at Marin (1996).
Variation of wake and thrust deduction fraction values plotted as a function of
apparent advance ratio J’ in the work
of Harvald (1977, 1967)
have clarified that both fractions are significantly dependent on the ship’s
speed and the rate of propeller revolution in four quadrant operation. Marin (1996) disclosed that despite both
fractions being almost independent of the ship’s speed, the wake fraction often
gradually decreases as the speed increases due to the correlation between the
viscous resistance coefficient and the wake fraction viscous component. On the
dependency on the propeller loading, it was claimed that both fractions most
commonly gradually decrease as propeller loading increases.
In
a later work by Artyszuk (2003),
the identification of both wake and thrust deduction properties from the
full-scale astern maneuvering trials failed due to some limitations. The work
then proposed a new general approach for determining thrust
deduction properties in the form of a differential equation (td) as a function of the
maneuvering time (t) by assuming the
wake fraction as constant. It is formulated as
Where vx, vy, ?z and m, m11, m22 correspond to surge, sway (positive to starboard), angular velocities, and ship mass, surge, and sway added mass while FxH and cm are hull resistance force and constant representing the hull positive thrust, respectively. However, modeling the thrust deduction fraction as a function of maneuvering time seems to be improper since the value is uncertain. As for comparison, Figure 6 depicts irregularities of the properties redrawn from stopping test results by Voorde (1974).
Figure 6
Thrust deduction fraction properties throughout stopping maneuvers
Avoiding
further inaccuracies in the modeling, Voorde (1974)
then assumed the factor to be constant and employed a value of (1-t) = 0.824 for determining the targeted
ship stopping ability and expressed the wake fraction from propeller
thrust and torque using Equation 10 and Equation 11 respectively whilst
neglecting Reynolds and Froude number effects.
In
a recent work of estimation of full-scale ship-stopping ability via a
free-running model test equipped with an auxiliary thruster, Ueno, Suzuki,and
Tsukada (2017) assumed wake factor (1-w) in astern maneuver as a constant
value as in conventional maneuvering of straight course for simplicity.
Meanwhile, the thrust deduction factor t
is treated as a whole function of the coefficient of longitudinal force induced
by reversing propeller denoted by (1–t)
KT. The coefficient is
given as a function of advance ratio J
to trade off the scale effect on the stopping maneuver since J which represents flow around the
propeller is common for both model and full-scale ships. However, the work
failed to solve the mathematical modeling employed and realize the full-scale
stopping maneuver using the test configuration due to limited knowledge of the
(1–t) KT factor. Seeking the possibility for evaluation of
ship-stopping ability from a practical point of view, the work insisted to
proceed further using such improper modeling.
3.4.3. Inaccuracy of dynamic ship
maneuvering performance prediction
IMO Manoeuvring Standards (IMO, 2002a, 2002b) has developed the framework for the evaluation of ship maneuvering performance ability as summarised in Figure 7. In contrast to other maneuverability assessments including inertial stopping ability, evaluation of ship (crash) stopping ability via stopping test is of a dynamic type and involves four quadrant propeller operation. The process encompasses acceleration to a test speed, deceleration to a designated reverse speed, and re-acceleration in an astern maneuver to zero speed (stop) condition.
Figure 7
IMO Manoeuvring Standards framework for stopping test (Sunarsih, 2018)
Despite
the complexity, the Standards allow prediction of ship-stopping ability and
demonstration of the behavior using calculation and/or computer simulation
programs based on a fairly simple mathematical model representing the important
aspects outlined in the framework. However, reliable predictions in such a
dynamic environment require proper modeling of the propeller forces for the
four quadrants of operations including the transition operations between the
quadrants and various wake and thrust deduction fractions (Hur,
Lee, and Chang, 2011; Hwang et al., 2003; Voorde, 1974).
Failure to meet such a requirement which lead to improper modeling of dynamic
hull-propeller interaction displayed by past researchers seemed to have caused
inaccuracies in the evaluations. As evidenced, several predictions
underestimated or overestimated the measured experimental or trial data while
some others underestimated and overestimated the values simultaneously. On top
of those, there existed some predictions which violated the criteria of
ship-stopping ability defined by the Standards.
Table
1 contrasts the full-scale measurement against the calculated stopping distance
S and time t obtained via two stopping tests extracted from the work of Voorde (1974).
Table 1 Calculated and measured
ship-stopping ability
As summarised in the table, variation of
added mass ?m by 6 % and 10 % of ship
mass m held a small effect in the
prediction of ship-stopping ability. Employing both values, the calculated
ship-stopping abilities consistently underestimated the measured stopping
distance while causing discrepancies in the prediction of the stopping time. In
Crash stop no. 2, the stopping time was underestimated for 8 s by 6 % added
mass while overestimated for only 2 s by 10 % added mass. In contrast, both 6 %
and 10 % added mass overestimated the stopping time of Crash stop no. 3 for as
long as 19 s and 26 s respectively. Voorde (1974) highlighted that despite
inaccuracies in the measurement of the stopping tests, large errors in the
prediction may arise from the assumption of thrust deduction fraction being
constant throughout the stopping maneuver.
Inaccurate
predictions also appeared in the work of Sung and Rhee (2005)
and Artyszuk (2011)
who employed constant propulsion factors in the proposed generic analytical
model for the determination of ship-stopping ability based on the Standards
framework (2002b,
2002a).
In the work of Sung and Rhee (2005),
the proposed model was unstably underestimated or overestimated the stopping
distance of particular ship types despite showing better agreement with the sea
trial data as compared to IMO (2002a) method qualitatively. Meanwhile, in the work of Artyszuk (2011),
the non-dimensional stopping distance s’total obtained reached 20 L which signifies a violation of the
Standards criteria by 15 L. Similar to Sung and Rhee (2005),
Artyszuk (2011)
expected the error to arise from the prediction of crash stopping distance
since the prediction of the coasting distance seems to be fine. Both works
highlighted that the proposed model requires further improvement with regards
to the crash-stopping model where the emphasis was given on the hydrodynamic
forces due to propeller reversal during the crash-stop maneuver and propeller
characteristic in crash-back operation.
In the work of Sutulo and Soares (2015), the simulation of a crash-stopping maneuver using the model developed yielded a considerably large error of up to 39.1 % as displayed in Table 2. On the other hand, the recorded surge velocity displayed a good agreement with the trial data. Such revelation is a bit odd since both parameters are closely related such that the distance the ship traveled is an integration product of the ship's velocity. The work stated that the error appeared due to rough modeling of the so-called Hovgaard force, a force caused by the influence of the tangential induced velocities in the slipstream of a heavily loaded propeller which occurs such as during the operation of crash-stop maneuver. Despite the claim, there is a strong possibility that design-based wake and thrust deduction fractions employed in the model contributed to the error in the prediction as found in other works detailed earlier.
Table 2 Measured and
simulated ship-stopping ability
|
Stopping
parameter |
Trial
data |
Simulation |
Error |
|
Final transfer |
1150
m |
700
m |
39.1
% |
|
Head reach |
2400
m |
2600
m |
8.3
% |
Later work by Ueno, Suzuki, and
Tsukada (2017)
revealed that similarity in the propeller reversing condition defined in the
modular mathematical model employed could not be ensured by the thruster fitted
in the ship model. After some modification to J and speed parameters, the simulation of the Full Astern stopping
test from Slow Ahead (SAH) of the target ship of KVLCC1 using the model
developed underestimated the head reach of the same ship as ITTC (2011)
benchmark data by 15.95 %. Surprisingly, the result of the experimental test
using a similar full-scale stopping maneuver free-running model test
configuration carried out obtained a better result whose error accounts for
only 1.45 %. Table 3 evaluates the accuracy of the simulation and experimental
results yielded by the work against the benchmark data supplemented by Transas Marine (2006).
Table 3 Accuracy of
the crash stop maneuvering simulation model and experimental result
|
Full
Astern from SAH |
Benchmark
data |
Simulation |
Error |
Experiment |
Error |
|
Head
reach |
6.9
L |
5.8
L |
15.95
% |
6.8
L |
1.45
% |
|
Initial
speed |
9.9
knot |
10
knot |
|
10
knot |
|
Inevitably, improper modeling of the
dynamic ship and propeller interactions in the form of single and constant or
ship parameter-based values led to large errors in the prediction of
ship-stopping ability as indicated by Hur, Lee, and Chang
(2011) and Voorde (1974) despite justifiable due to the
lack of knowledge and data in the field. Hur, Lee, and Chang
(2011) who evaluated propeller loads
during crash stop emphasized that wake fraction has to change according to ship
speed to obtain more accurate results in the prediction of ship stopping
ability. Correspondingly, Wirz (2012)
who performed optimization of the crash stop maneuver claimed that any approach
in the optimization of the stopping maneuver should focus on the reversing
speed as hull-propeller interaction becomes more intense during such period. As
a guideline for a valid prediction as par to the benchmark data recommended by ITTC (2011)
and comply with the Standards (IMO, 2002a) criteria of ship stopping
ability, the mathematical modeling and assumption of the components employed
should be able to capture all ship behavior during a stopping maneuver.
Highlights
have been given on the scarcity of knowledge and data of the four quadrant wake
and thrust deduction fraction properties depicting various maneuvering
conditions and current simplistic approaches in handling the limitations. The
inaccuracy of the current ship maneuvering predictions employing invalid values
and improper models for the sake of such simplicity has been disclosed thoroughly.
There exists the urgency of the accumulation of new knowledge and data on the
properties to the extent of remodeling the current mathematical model to enable
the representation of the real ship maneuvering behavior in various operating
conditions.
| Filename | Description |
|---|---|
| R2-ME-5489-20220317161137.docx | --- |
Artyszuk, J.,
2003. Wake Fraction and Thrust Deduction During Ship Astern Manoeuvres. In: Marine Technology V: Fifth International
Conference on Marine Technology and Transportation, Volume 2003, pp. 125–134
Artyszuk, J.,
2011. Propulsive and Stopping Performance Analysis of Cellular Container
Carriers. In: Miscellaneous Problems in Maritime Navigation, Transport and
Shipping: Marine Navigation and Safety of Sea Transportation. 1st
Edition. London: CRC Press
Benvenuo, G., Brizzolara,
S., Figari, M., 2001. Simulation of the Propulsion System Behavior during Ship
Standard Maneuvers. In: Proceedings
of the Eighth International Symposium on Practical Design of Ships and Other
Floating Structures, Volume 2001, pp. 657–663
Cimen, T., 2009.
Development and Validation of a Mathematical Model For Control of Constrained
Non-Linear Oil Tanker Motion. Mathematical and Computer Modelling of
Dynamical Systems, Volume 15(1), pp. 17–49
Cui, J., Wu, Z.,
Chen, W., 2018. Research on Prediction of Ship Manoeuvrability. Journal of
Shipping and Ocean Engineering, Volume 8, pp. 30–35
Harvald, S.A.,
1967. Wake and Thrust Deduction at Extreme Propeller Loadings. Stevens
Institute of Technology, Volume 61
Harvald, S.A., 1976.
Factors affecting the stopping ability of ships. International Shipbuilding
Progress, Volume 23, pp. 106–121
Harvald, S.A.,
1977. Wake and Thrust Deduction at Extreme Propeller Loadings For a Ship
Running in Shallow Water. Transactions of the Royal Institution of Naval
Architects, Volume 119, pp. 213–236
Hideo, S., Oh,
C.D., 1971. A Method of Analyzing Propulsive Test Results of Full Ship Models. Journal
of the Kansai Society of Naval Architects of Japan, Volume 139, pp. 25–42
Holtrop, J.,
1984. A Statistical Re-Analysis of Resistance and Propulsion Data. International
Shipbuilding Progress, Volume 31, pp. 272–276
Holtrop, J.,
Mennen, G.G.J., 1982. An Approximate Power Prediction Method. International
Shipbuilding Progress, Volume 29(335), pp. 166–170
Hur, J.W., Lee,
H., Chang, B.J., 2011. Propeller Loads Of Large Commercial Vessels at Crash
Stop. Second International Symposium on Marine Propulsors smp, Volume 11
Hwang, W.,
Jakobsen, B., Barr, R., Ankudinov, V., Fuller, N., Vest, L., Morris, M.,
Mcgovern, A., Landsburg, A., 2003. An Exploratory Study to Characterize Ship
Manoeuvring Performance at Slow Speed. In: International Conference of
Manoeuvring and Control–MCMC2003. Kanazawa, Japan
Illes, L.,
Jurkovic, M., Kalina, T., Gorzelanczyk, P., Luptak, V., 2021. Methodology for
Optimising The Hull Shape of a Vessel With Restricted Draft. Scientific
Journal of Silesian University of Technology, Series Transport, Volume 110,
pp. 59–71
Illes, L.,
Kalina, T., Jurkovic, M., Luptak, V., 2020. Distributed Propulsion Systems for
Shallow Draft Vessels. Journal of Marine Science and Engineering, Volume
8, pp. 1–17
International
Maritime Organization (IMO), 2002a.
Explanatory Notes to the Standards for Ship Manoeuvrability, Annex 2.1. 2, 2.1.
5 (MSC/Circ. 1053)
International
Maritime Organization (IMO), 2002b.
Standards for Ship Manoeuvrability. Resolution MSC.137(76)
International
Towing Tank Conference (ITTC), 2011. Recommended Procedures and Guidelines
7.5-02/06-03: Validation of Manoeuvring Simulation Models. In: 26th
ITTC Manoeuvring Committee, pp. 1–11
Lewis, E.V.,
1988. Principles of Naval Architecture Second Revision. Jersey: Sname,
Volume 2, pp. 152–157
MARIN, 1996. Resistance
and Propulsion. Maritime Research Institute Netherlands
Nakato, M.,
Kose, K., Terarnoto, S., Simamune, S., 1976. Experimental Study on Accelerating
and Decelerating Ship Motions. Journal of the Society of Naval Architects of
Japan, Volume 1976, pp. 77–84
Oneto, L.,
Coraddu, A., Cipollini, F., Karpenko, O., Xepapa, K., Sanetti, P., Anguita, D.,
2018. Crash Stop Maneuvering Performance Prediction: a Data-Driven Solution for
Safety and Collision Avoidance. Data-Enabled Discovery and Applications,
Volume 2, pp. 1–11
Paroka, D.,
Muhammad, A.H., Asri, S., 2017. Prediction of Ship Turning Maneuvers in
Constant Wind and Regular Waves. International Journal of Technology,
Volume 8(3), pp. 387–397
Pérez, F.L.,
Clemente, J.A., 2007. The Influence of Some Ship Parameters on Manoeuvrability
Studied at The Design Stage. Ocean Engineering, Volume 34, pp. 518–525
Prabowo, A.R.,
Bae, D.M., Sohn, .J.M., Zakki, A.F., 2016. Evaluating the Parameter Influence
in the Event of a Ship Collision based on the Finite Element Method Approach. International
Journal of Technology, Volume 7(4), pp. 592–602
Priadi, A.A.,
Tjahjono, T., 2015. Implementation of Traffic Separation Scheme For Preventing
Accidents on The Sunda Strait. International Journal of Technology, Volume
6, pp. 990–997
Sunarsih, 2018. Four
Quadrant Thrust Generation Model with Bounded Dynamic Wake and Thrust Deduction
Fractions. Universiti Teknologi Malaysia
Sunarsih,
Izzuddin, N., Priyanto, A., 2015. Thrust and Torque Estimation Scheme Based on
Chebyshev Polynomial for Ship Manoeuvring Simulation. Procedia
Manufacturing, Volume 2, pp. 359–363
Sung, Y.J.,
Rhee, K.-P. 2005. New Prediction Method On The Stopping Ability Of Diesel Ships
With Fixied Pitch Propeller. International Shipbuilding Progress, Volume
52, pp. 113–128
Sutulo, S.,
Soares, C.G., 2011. Mathematical Models For Simulation of Manoeuvring
Performance of Ships. Marine Technology and Engineering, Soares, G.,
Garbatov, C., Fonseca, Y., Teixeira, A.P., (ed.), Taylor & Francis Group,
London, pp. 661–698
Sutulo, S.,
Soares, C.G., 2015. Development of a Core Mathematical Model for Arbitrary
Manoeuvres of a Shuttle Tanker. Applied Ocean Research, Volume 51, pp. 293–308
Tani, H., 1968.
The Reverse Stopping Ability of Supertankers. The Journal of Navigation,
Volume 21, pp. 119–154
Taylor, D.W., 1910.
The Speed and Power of Ships. A Manual of Marine Propulsion. New York,
USA: John Wiley & Sons
Transas Marine,
2006. Manoeuvring Booklet V1.06: Mathematical Model of VLCC 2 (Dis.127691t)
bl. UK: TRANSAS Marine Ltd
Trodden, D.,
Haroutunian, M., 2018. Effects of Ship Manœuvring Motion on No X Formation. Ocean
Engineering, Volume 150, pp. 234–242
Ueno, M.,
Suzuki, R., Tsukada, Y., 2017. Estimation of Stopping Ability of Full-Scale
Ship Using Free-Running Model. Ocean Engineering, Volume 130, pp. 260–273
Vanem, E.,
Antão, P., Ostvik, I., De Comas, F.D.C., 2008. Analysing The Risk of LNG
Carrier Operations. Reliability Engineering & System Safety, Volume 93,
pp. 1328–1344
Voorde, V.D.,
1974. Calculations and Experiments with Regard to The Stopping of a Ship With
Diesel Propulsion and Fitted With a Controllable Pitch Propeller. Netherlands: Netherlands
Ship Research Centre TNO
Wirz, D.-I.F.,
2012. Optimisation of The Crash-Stop Manoeuvre of Vessels Employing Slow-Speed
Two-Stroke Engines and Fixed Pitch Propellers. Journal of Marine Engineering
& Technology, Volume 11, pp. 35–43
Ye, B., Wang,
Q., Wan, J., Peng, Y., Xiong, J., 2012. A Four-Quadrant Thrust Estimation
Scheme Based on Chebyshev Fit and Experiment of Ship Model. Open Mechanical
Engineering Journal, Volume 6, pp. 148–154
