Analysis of Bittern Recovery Facility Using Mixed-Integer Nonlinear Programming: Centralized, Decentralized, and Hybrid Scenarios
Corresponding email: erwin@ie.its.ac.id
Published at : 09 May 2023
Volume : IJtech
Vol 14, No 3 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i3.5437
Widodo, E., Putra, F.S.U., Hartanto, D., Arvitrida, N.I., Bagastyo, A.Y., Warmadewanthi, I., Soehartanto, T., 2023. Analysis of Bittern Recovery Facility Using Mixed-Integer Nonlinear Programming: Centralized, Decentralized, and Hybrid Scenarios. International Journal of Technology. Volume 14(3), pp. 638-648
| Erwin Widodo | Industrial and Systems Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| Furqon Sandiva Utomo Putra | Industrial and Systems Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| Dody Hartanto | Industrial and Systems Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| Niniet Indah Arvitrida | Industrial and Systems Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| Arseto Yekti Bagastyo | Environmental Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| IDAA Warmadewanthi | Environmental Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
| Totok Soehartanto | Instrumentation Engineering, Institut Teknologi Sepuluh Nopember, Surabaya, 60111, East Java, Indonesia |
The desalination process to produce salts leaves wastewater with a high concentration of minerals called bittern. Most salt producers dump bittern straight away. Such disposal is dangerous to the ecosystem since bittern may increase the environmental salinity. Furthermore, bittern still has potential as it contains minerals that can be extracted and offers value. Consequently, further bittern treatment is necessary to reduce the environmental impact and create a circular economy. However, some specific requirements are needed in determining how to carry out this recovery process. In that, recovery managers need to know the most suitable type and optimal operation variables. These are essential to meet cost-effectiveness and environmental benefits. This research proposes a mixed-integer nonlinear programming (MINLP) model for analyzing the supply and demand of the bittern recovery. This study offers a model to optimize the trade-off between cost and benefits of the recovery process. There are three scenarios to determine the best bittern recovery practices: centralized, decentralized, and hybrid scenarios. The proposed models are then tested and analyzed for their sensitivity due to essential parameters. The numerical analysis has shown that a centralized scenario is best suited for a region with a low bittern supply. Moreover, a hybrid scenario is best suited in an area with a higher bittern supply. In addition, a decentralized scenario is the most suitable option for a region where the number of salt farms is high, and the location is far from the recovery facility.
Bittern recovery; Circular economy; Mixed-integer nonlinear programming
Let us take a prominent example in a country with vast
salt consumption, Indonesia. Data have shown that Indonesia produced 2,349,629
metric tons of salt in 2018 (Ministry
of Maritime Affairs and Fisheries, 2019). In this
country, salts are produced through multilevel processing. The evaporation
process of seawater is carried out in the evaporator area. The crystallization
process is undertaken in a specific area
Commonly, bitterns are considered
waste and never used again. This waste is problematic because although bittern
water contains similar compounds to seawater, it is much more concentrated.
When bittern is directly dumped into the ecosystem, the increase in salinity
may harm the life in the area (Tewari,
2003). Furthermore, treating bittern solely as an unused
by-product of salt production is also a waste of potential since it still
contains minerals that can be extracted and have selling value. For every 10
million tons of salt produced, below is the composition of chemicals found in
the bittern:
Table 1 Chemical contained in bittern from 10 million tons of
salt produced (Abdel-Aal,
Zohdy, and Abdelkreem, 2017)
|
Chemical compound |
Tons |
|
NaCl |
1,500,000 |
|
MgCl2 |
1,200,000 |
|
MgSO4 |
700,000 |
|
KCl |
238,000 |
|
Bromine |
20,000 |
Those chemicals can still be utilized in other industries, such as
cosmetics, energy drinks, and salt industries, for the second time. This
estimation shows the potential that can be exploited by treating bittern. Thus,
bittern recovery in the salt industry can reduce the environmental impact of
salt production but also create a circular economy, which is a system that
focuses on reusing, recycling, and recovering to achieve sustainability (Sauvé,
Bernard, and Sloan, 2016).
Applying the economic concept would contribute to the environment and yield
society-wide benefits (Berawi,
2020). Furthermore, it will also follow the sustainable
development concept, a balance of economic growth and ecological regeneration (Berawi, 2019).
However, this requires a complex
process to maximize the efficiency and effectiveness of the bittern recovery.
One needs to know the optimal type and number of recovery stations, considering
the bittern supply chain availability and the demand for the extracted mineral.
It also needs to be cost-efficient and yield a beneficial result. An approach
that can meet this objective is mixed-integer nonlinear programming (MINLP).
MINLP is mathematical programming
that has continuous and discrete variables and nonlinearities within its
objective function and constraints (Bussieck and Pruessner,
2003). It has a wide range of use,
including in the process industry, chemical engineering, and manufacturing. We
used this model in a bittern recovery system because some values of variables,
such as the number of recovery facilities, need to be an integer, while others
(such as cost) do not. Furthermore, as the research objective maximizes circular
economy, the function has a non-convex element related to diminishing returns
and economies of scale, hence the need to include nonlinearity in the
programming.
In achieving a circular economy
in wastewater treatment, previous research has studied a circular economy and
cleaner production model. This research optimized product-machine allocation
using MILP (Rajput and Singh, 2020). Another research on wastewater treatment management that considers
both the economy and environment also implemented the MILP approach (Henriques et al., 2020; Zhou et al., 2020; Durkin, Millan-Agorio,
and Guo, 2020). In terms of using the MINLP
approach, a previous study has proposed a framework that considers the cost and
benefit of wastewater treatment (Padrón-Páez, Almaraz, and
Román-Martínez, 2020).
In the field of wastewater
treatment, several breakthroughs have been proposed. Cotton and carbon material
filter was implemented since they offer high sorption
capacities and simple preparation processes (Politaeva et al., 2020). In
addition, an anaerobic fixed bed reactor (AFBR) was proposed to reduce the odor
due to the high protein content in industrial wastewater (Purnomo, Mawaddah, and
Bayonita, 2021). Furthermore, Biofloc Technology and Effective Microorganism
S4 (EM4) have been attempted to be successful in reducing ammonia and nitrate
concentration in the shrimp agro-industry (Suwartha and Pujiastuti, 2017). Moreover, nanofiltration technology
was also observed and successfully proven to remove remazol red dye, indigosol
brown dye, and sodium sulfide (Na2S) in the batik textile industry (Istirokhatun et al.,
2021).
The present study aims to
implement the MINLP model for achieving a circular economy, specifically the
bittern recovery process. Furthermore, this research extends the scope by
comparing possible bittern recovery scenarios between centralized,
decentralized, or hybrid types of recovery stations to see which scenario would
be the best to apply to certain conditions. The other kind of recovery scenario
needs to be weighed in as it affects effectiveness and cost-efficiency. Both
profit maximization and the recovery process's environmental impact are
considered.
This research considered some
factors from the bittern's supply, demand structure, and recovery process
constraints. The model is used to maximize the profit by optimizing the
trade-off between the cost of waste transportation, recovery, and station
investment, benefiting from the selling value of the recovered minerals and the
environmental sustainability.
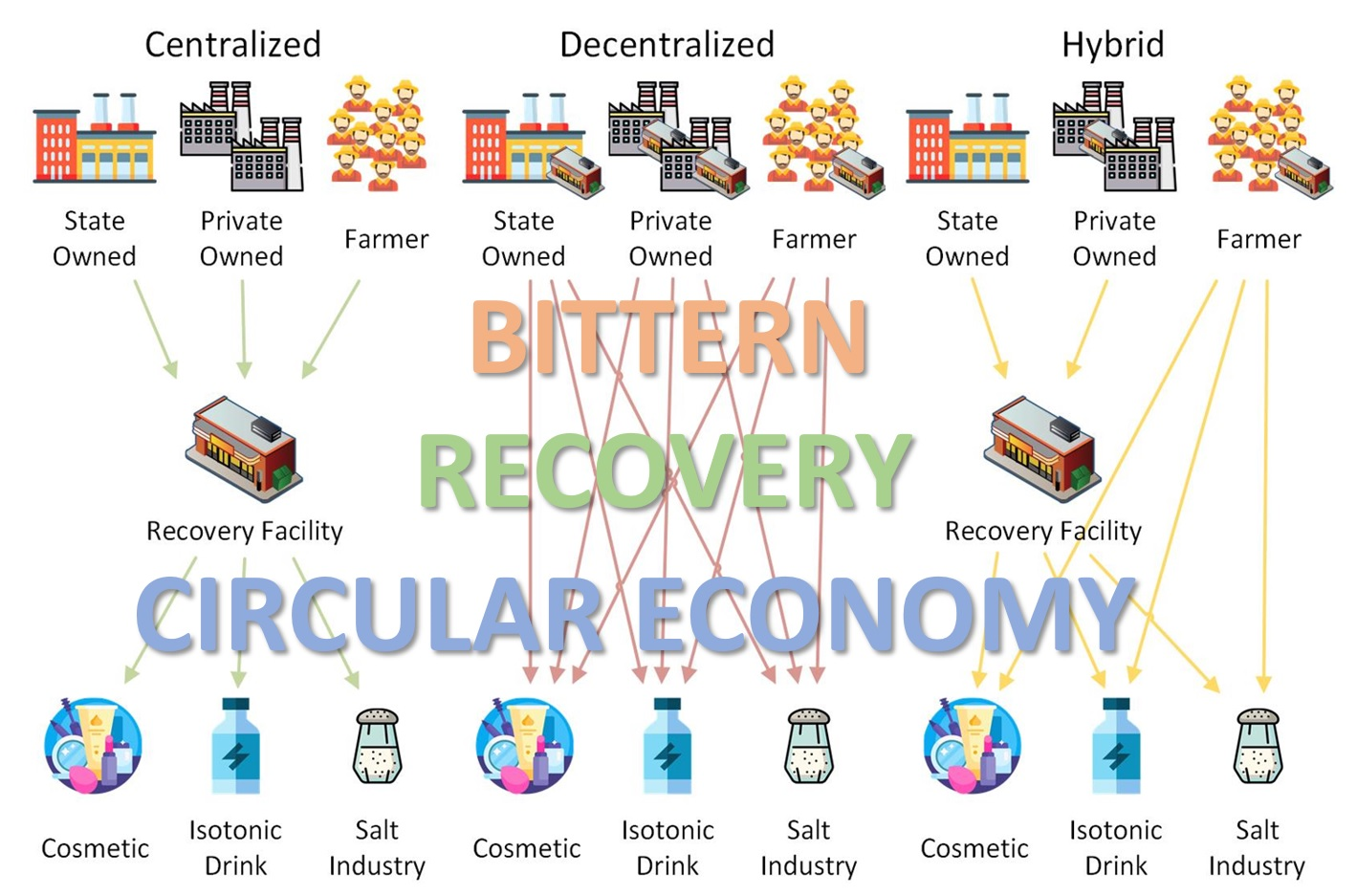
2.1. Conceptual Model
The
system discussed is a combination of the supply, demand, and bittern recovery
facility. The supplier of bittern, in this case, came from 3 types of salt
industries: state-owned industry, privately owned industry, and salt farmers.
This differentiation creates the assumption that each industry type has a
different amount of output and amount of entity. In that, state-owned and
private-owned industries will have larger salt output but fewer entities than
salt farmers. The consumer who demands the chemical gained from the bittern
recovery process comes from the cosmetic, isotonic, and salt industries, and
each requires a different chemical extracted. The bittern recovery facility
scenario that would be considered in this research is as follows:
A centralized system has a
single location that handles the bulk of the demand for bittern recovery. While
decentralized means the organization will have multiple treatment hubs as close
as possible to the source of bittern, working simultaneously to cover a broader
range (Libralato, Volpi, and Avezzu,
2012).
Figure 1 The supply chain flow between the salt industry, bittern recovery
facility, and consumers in different scenarios
The
above sub-system, later on, will be expressed in cost and benefits variables.
The cost variables are facility investment, the bittern recovery process,
material handling, and transportation costs. At the same time, the benefit
variables came from the revenue from selling the extracted chemical to the
consumers and the economic valuation of the environmental benefit from
recovering the bittern. The model is also subjected to the amount of bittern
supplied, the chemical demanded, and the facility's capacity.
2.2. Mathematical Model
The model is based on
MINLP, mathematical modeling involving discrete variables and nonlinear
constraint functions (Leyffer et al.,
2009). For each scenario described, a
model is developed as follows:
2.2.1. Centralized
Scenario
Objective function:
Constraint:
3. Demand is assumed to be equal to the mass of chemicals supplied due to implementing a pull system.
2.2.2. Decentralized
Scenario
Objective function:
As each salt producer has its bittern recovery
facility, inbound transportation cost and material handling are assumed to be
zero. Constraints (10) to (16) were then applied.
2.2.3. Hybrid
Scenario
Objective function:
Max profit (Z) = Max profit Centralized + Max profit
decentralized
A new index (l) is introduced to differentiate the
centralized and decentralized equation to solve this. The centralized max profit
is as follows:
While the
decentralized max profit is as follows:
The mathematical models are then run into LINGO, a
tool to build and solve linear, nonlinear, quadratic, stochastic, and integer
optimization programming (LINDO, n.d.). The data of environmental benefits is approximated
from the literature review, while transportation cost and material handling
costs are approximated using the local gas price and labor cost.
3.1. Model
Running Results
Below are the results of the model
running test:
Table 1 Model running results (in a million rupiah)
|
Centralized |
Decentralized |
Hybrid | |
|
Total Revenue |
563,169.6 |
606,015.7 |
395,461.6 |
|
Environmental Benefit |
117,659.3 |
114,279.2 |
43,136.38 |
|
Investment Cost |
1,000 |
500 |
1,350 |
|
Inbound transportation cost |
58.226340 |
- |
56,895 |
|
Inbound material handling |
85,315.53 |
- |
11,671.07 |
|
Outbound transportation cost |
117,355.4 |
201,851.3 |
111,487.65 |
|
Outbound material handling |
14,444.12 |
14,444.12 |
9,388.676 |
|
Recovery cost |
61,880 |
309,400 |
114,478 |
Our calculation assumes that the environmental benefit was
gained through economic valuation by performing wastewater treatment (Hernández-Sancho,
Molinos-Senante, and Sala-Garrido, 2010). Our numerical
experiment shows that the centralized scenario yields the highest profit at the
value of Rp 400,833.9 million, followed by the decentralized with Rp 193,599.5
million and the hybrid scenario with Rp190,222.5 million. When we compare the
revenues under centralized and decentralized scenarios, the latter is slightly
higher than the former. Nonetheless, the decentralized scenario yields lower
overall profit than that under centralized. The reason is the total processing
cost of a decentralized scenario is way higher than the centralized one.
Another reason is centralized scenario experience benefits from an economic
scale. This situation makes its corresponding investment considerably cheaper (Mourtzis and
Doukas, 2012). When we proceed to the following comparison
between decentralized and hybrid scenarios, the former yields higher profit
than the latter. This is due to higher facility investment costs under the
hybrid scenario. In addition, both scenarios still incur considerably high
inbound transportation and material handling costs.
To compare our results to those with
similar works of centralized versus decentralized and hybrid concepts for water
waste treatment, we reviewed some related articles. By using specially
constructed wetlands in China, decentralized and sometimes hybrid wastewater
systems may overcome the efficiency of the centralized system (Ying et al., 2021). This
fact is contrary to our initial numerical experiment results. In addition, a
study of non-targeted analysis with gas chromatography-spectrometry
was conducted to evaluate the performance of centralized versus decentralized
water waste systems in the USA and South Africa (Mladenov
et al., 2022). Surprisingly, the
decentralized system was found to perform better than the centralized one.
Moreover, a study to assess
the efficiency of rural sewage treatment (RuST) was conducted by using
centralized and decentralized scenarios (Yuansheng
et al., 2021). An interesting
result was revealed when it was found that the centralized scenario does not
always provide the best result. By proposing rural residents' spatial pattern
(RESP) and the optimal pattern of RuST, a decentralized scenario offers a
better outcome for water waste treatment.
We decided to proceed with our numerical
experiment further based on those aforementioned exciting facts. As the primary
purpose of this research is to create a model that can be used in
decision-making, it is not enough to have a single result, as shown in Table 1.
Thus, sensitivity analysis is applied to two important parameters in our
proposed model: annual bittern supplied and the proportion of salt produced by
each industry type.
3.2. Profit
sensitivity on annual bittern supply
Figure 2 Profit sensitivity on the changes in annual bittern supply
Predictably, the total profit would
exponentially increase with more supply of bittern. However, each scenario
would eventually reach its infeasible point, meaning it can no longer fulfill
the constraints due to the cost incurred becoming too high. The centralized
scenario is the first to do so. The reason is that with the highest material
handling and transportation cost that linearly increases with the rise of
bittern supply, it reaches a point where it is no longer economically feasible.
This situation happens when the bittern supply reaches 1.25 million tons per
year.
Moreover, the decentralized scenario
became infeasible when the bittern supply reached 1.5 million tons per year.
The reason is the processing cost became too overwhelming, and the revenue
could not keep up. The outbound transportation cost also became too expensive
as it needed to transport the resulting chemicals to each buyer from each of
the respective salt farms. Additionally, while applying the decentralized
scenario to the 1.25 million tons supply mark is still feasible, the hybrid scenario
has become more profitable. The reason is that it has a much lower recovery
cost than the decentralized scenario. The scenario would remain feasible until
the bittern supply reaches 2 million tons annually.
Thus, if the decision-maker intends to utilize
the full extent of bittern available in their region, it is more recommended to
use the hybrid scenario to accommodate a larger volume.
3.3. Profit
sensitivity on the proportion of salt produced from industry type
Figure 3 Profit sensitivity on the changes in the proportion of salt
produced in each industry type
The analysis shows that
both decentralized and hybrid scenarios would increase profit as salt farmers'
proportion of salt increases. The reason is that inbound transportation and
material handling costs will reduce if more bitterns are processed in-house.
Increasing the bittern percentage supplied by salt farmers would eventually
make the decentralized scenario more profitable than the centralized one.
However, when looking at
how the proportion of state-owned and private-owned industries is divided, it
shows different tendencies. While the hybrid scenario would exponentially
increase profit, the decentralized scenario would be flatter. Although not by a
large margin. The reason is that private-owned and state-owned industries have
fewer plan quantities than salt farmers, benefiting from the economy of scale
of a centralized recovery facility than a decentralized one. This decentralized
scenario would eventually be less profitable than a hybrid scenario when the
salt farm proportion is not overwhelmingly dominating compared to the other two
industry types.
As an interesting note, even
though it is considered a "salt farmer" in this research, the same
principle is also applied in the condition where the salt farms in a region are
a lot and far in between, regardless of the owner of said factory. Thus, a
decentralized scenario would be preferable if a decision-maker wants to apply a
bittern recovery scenario in a region where that situation is prominent.
The research has proposed three
different scenarios of the bittern recovery process. Each scenario could be
profitable when applied to certain conditions. Our numerical experiment has
successfully shown some model behavior as evidence on which scenario is more
financially preferable to use. However, the implementation of such scenarios
would depend on several different circumstances. Our proposed model set works
based on profit optimization. Such mathematical representation can provide some
optima in a numerical result of decision variables that maximizes circular
economy benefit. This process is done by maximizing the revenue items
consisting of the cost of extracted chemicals and environmental benefits and
minimizing the associated cost, including transportation, material handling,
investment, and recovery cost. Some insights derived from our analysis can
assist decision-makers of bittern recovery processes in selecting which bittern
recovery scenario is the best-suited option. The centralized scenario is best
suited when in a region with a low bittern supply. The hybrid scenario is best
suited in a region with a higher bittern supply. The decentralized scenario is
best for a region where the salt farms are a lot and far in between. Nonetheless,
there are some limitations and drawbacks to this research. Hence, some
betterment is interesting as future works are done by transforming the model
into a dynamic model instead of a deterministic one, allowing for more accurate
results. Future works can also expand the model for other scenarios.
The
authors gratefully acknowledge the two (2) financial support for this work from
the Indonesian Ministry of Education, Culture, Research, and Technology in
Institut Teknologi Sepuluh Nopember, ITS, Surabaya. First is Collaboration
Research Scheme in Direktorat Riset dan Pengabdian Masyarakat in 2021 (Research
and Community Service Directorate) with grant number D72021 – Dana ITS
(Consortium). Second is Program Kompetisi Kampus Merdeka 2021 (Independent
Campus Competition Program), organized by the Industrial and Systems
Engineering Department.
Abdel-Aal, H., Zohdy, K., Abdelkreem, M., 2017. Seawater Bittern a
Precursor for Magnesium Chloride Separation: Discussion and Assessment of Case
Studies. International Journal of Waste Resources, Volume 7(1), pp. 1–6
Berawi, M.A., 2019. The Role of
Industry 4.0 in Achieving Sustainable Development Goals. International
Journal of Technology, Volume 10(4), pp. 644–647
Berawi, M.A., 2020. Managing
Nature 5.0: The Role of Digital Technologies in the Circular. International
Journal of Technology, Volume 11(4), pp. 652–655
Bussieck, M.R., Pruessner, A.,
2003. Mixed-Integer Nonlinear Programming. Washington: GAMS Development
Corporation
Durkin, A., Millan-Agorio, M.,
Guo, M., 2020. Process Systems Design Framework for Resource Recovery from
Wastewater. Computer Aided Chemical Engineering, Volume 48, pp. 1039–1044
Henriques, A.A., Fontes, M., Camanho,
A., Silva, J.G., Amorim, P., 2020. Leveraging Logistics Flows to Improve the
Sludge Management Process of Wastewater Treatment Plants. Journal of Cleaner
Production, Volume 276(2), p. 122720
Hernández-Sancho, F.,
Molinos-Senante, M., Sala-Garrido, R., 2010. Economic Valuation of
Environmental Bene?ts from Wastewater Treatment Processes: an Empirical
Approach for Spain. Science of the Total Environment, Volume 408(4), pp.
953–957
Istirokhatun, T., Susanto, H.,
Budihardjo, M.A., Septiyani E., Wibowo, A.R., Karamah E.F., 2021. Treatment of
Batik Industry Wastewater Plant Effluent using Nanofiltration. International
Journal of Technology, 12(4), pp. 770–780
Leyffer, S., Linderoth, J.,
Luedtke, J., Miller, A., Munson, T., 2009. Applications and Algorithms for
Mixed Integer Nonlinear Programming. Journal of Physics: Conference Series,
Volume 180, p. 012014
Libralato, G., Volpi, A., Avezzù, G. F., 2012. To centralise or to
decentralise: An Overview of The Most Recent Trends in Wastewater Treatment
Management. Journal of Environmental Management, Volume 94(1), pp. 61–68
LINDO, n.d. LINGO 19.0 -
Optimization Modeling Software for Linear, Nonlinear, and Integer Programming.
Available at: https://www.lindo.com/index.php/products/lingo-and-optimization-modeling,
Accessed on May 20, 2022
Ministry of Maritime Affairs and
Fisheries, 2019. Produksi Garam (Salt Production). Kementerian Kelautan
dan Perikanan Republik Indonesia
Mladenov, N., Dodder, N.G.,
Steinberg, L., Richardot, W., Johnson, J., Martincigh, B.S., Buckley, C.,
Lawrence, T., Hoh, E., 2022. Persistence and Removal of Trace Organic Compounds
in Centralized and Decentralized Wastewater Treatment Systems. Chemosphere,
Volume 286(1), p. 13162
Mourtzis, D., Doukas, M., 2012.
Decentralized Manufacturing Systems Review: Challenges and Outlook. Logistic
Research, Volume 5, pp. 113–121
Padrón-Páez, J.I., Almaraz,
S.D.-L., Román-Martínez, A., 2020. Sustainable Wastewater Treatment Plants
Design Through Multiobjective Optimization. Computers & Chemical
Engineering, Volume 140(2), p. 106850
Politaeva, N., Taranovskaya, E.,
Mukhametova, L., Ilyashenko, S., Atamanyuk, I., Afif, R.A., Pfeifer, C., 2020.
Cotton Fiber and Carbon Materials Filters for Efficient Wastewater
Purification. International Journal of Technology, Volume 11(8), pp.
1608–1617
PT Garam, 2018. Profil Perusahaan
(Company Profile). Available at: https://www.ptgaram.com/profilperusahaan, Accessed
on June 12, 2020.
Purnomo, C., Mawaddah, M.E., Bayonita, S., 2021. The Simulation and
Experimental Study of COD Removal from Rubber Industrial Wastewater using
Anaerobic Fixed Bed Reactors. International Journal of Technology,
Volume 12(2), pp. 320–328
Rajput, S., Singh, S.P., 2020.
Industry 4.0 Model for Circular Economy and Cleaner Production. Journal of
Cleaner Production, Volume 277, p. 123853
Sauvé, S., Bernard, S., Sloan,
P., 2016. Environmental Sciences, Sustainable Development and Circular Economy:
Alternative Concepts for Trans-Disciplinary Research. Environmental
Development, Volume 17, pp. 48–56
Suwartha, N., Pujiastuti, D.R.,
2017. Enhancing Removal Efficiency of Ammonia and Nitrate in Shrimp Farm
Wastewater Using Biofloc Technology and Effective Microorganism S4 (EM4). International
Journal of Technology, Volume 8(6), pp. 1021–1030
Tewari, A., 2003. The effect of
sea brine and bittern on survival and growth of mangrove Avicennia marina
(Dicotyledones: Avicenniaceae). Indian Journal of Geo-Marine Sciences, Volume
32(1), pp. 52–56
Ying, F., Wu, X., Shao, L., Han,
M., Chen, B., Meng, J., Wang, P., Chen, G., 2021. Can Constructed Wetlands Be
More Land Efficient Than Centralized Wastewater Treatment Systems? A Case Study
Based on Direct and Indirect Land Use. Science of The Total Environment,
Volume 770, p. 144841
Yuansheng, H., Li, P., Li, H.,
Zhang, B., He, Y., 2021. To Centralize or To Decentralize? A Systematic
Framework for Optimizing Rural Wastewater Treatment Planning. Journal of
Environmental Management, Volume 300, p. 11367
Zhou, X., Zhang, H., Long, Y.,
Song, M., Qiu, R., Yan, Y., Liang, Y., 2020. Sustainable And Clean Oilfield
Development: Optimal Operation of Wastewater Treatment And Recycling System. Journal
of Cleaner Production, Volume 252, p. 119819
