Analysis of Combined Braking Torque on The Regenerative Anti-Lock Braking System in The Quarter Electric Vehicle Model
Corresponding email: katherin@ep.its.ac.id
Published at : 17 May 2024
Volume : IJtech
Vol 15, No 3 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i3.5265
Indriawati, K., Sudarmanta, B., Widjiantoro, B.L., Hafiizh, N.A., Said, A.H., 2024. Analysis of Combined Braking Torque on The Regenerative Anti-Lock Braking System in The Quarter Electric Vehicle Model. International Journal of Technology. Volume 15(3), pp. 628-640
| Katherin Indriawati | Department of Engineering Physics, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo–Surabaya, 60111, Indonesia |
| Bambang Sudarmanta | Department of Mechanical Engineering, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo–Surabaya, 60111, Indonesia |
| Bambang Lelono Widjiantoro | Department of Engineering Physics, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo–Surabaya, 60111, Indonesia |
| Nur Adlun Hafiizh | Department of Engineering Physics, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo–Surabaya, 60111, Indonesia |
| Ahmad Hazmi Said | Department of Engineering Physics, Institut Teknologi Sepuluh Nopember, Kampus ITS Sukolilo–Surabaya, 60111, Indonesia |
The
regenerative ABS is developed to avoid slip and to regenerate energy using two
types of braking: friction and motor. This paper discusses the experimental
results of combining the two types of braking which are applied to a
quarter-electric vehicle model. The control algorithm is developed using
sliding mode control (SMC), where continuous action is performed to produce
motor braking torque while discrete action is performed to produce hydraulic
braking torque (friction). Furthermore, the proposed control system also
implements control coordination to distribute braking torque, enhances the
occurrence of the non-slip process, and generates energy for vehicle batteries.
From the experimental results, it is concluded that the slip ratio value can be
used to obtain the optimum conditions for the braking process, where the
hydraulic torque as the cause of the slip, is limited through the braking
distribution algorithm. The proposed control system produces a response with a
brake speed of 2 m/s and a 3.39% increase in battery SOC.
Anti-lock braking system; Control coordination; Regenerative; Sliding mode control
One of
the efforts to reduce the negative impact of fossil fuel vehicles is the
development and use of electric vehicles. Generally, when braking occurs,
energy is wasted in the form of heat due to friction between the brake pads and
the wheels. Energy wastage is an important issue, especially for electric
vehicles. Therefore, this led to the design of a regenerative braking system
capable of converting kinetic energy into electricity when vehicles decelerate.
This energy is then stored in batteries for reuse, thereby increasing vehicle
efficiency (Usman et al., 2016; Benetti et al.,
2014; Faria and Delgado, 2014). The braking torque is generated by the
motor driving the vehicle. The results showed that the energy storage achieved
by this system is in the range of 8%-25% of the total energy used by the
vehicle, which is dependent on the regulatory cycle and control strategy, in
addition to manipulation of braking components such as the use of electric
brake boosters which can reduce electricity consumption (Nugraha et al., 2021; Shah et
al., 2018; Yu, Liu and Liu, 2016). Conversely, the braking torque
of the motor is often not capable of braking quickly, due to many influencing
factors,
such
as
motor speed, charging
status,
and battery temperature (Rajendran et al., 2018; Li, Du, and Li, 2016; Tehrani
et al., 2011; Zhang, Yin, and Zhang,
2010). Therefore, the process of braking with hydraulic torque is still
needed.
Generally, the
braking system plays an essential role in the safety of vehicles. The latest
technology commonly used to prevent the wheels of vehicles from being locked
during the sudden application of brakes is the anti-lock braking system (ABS).
According to preliminary studies, sudden braking leads to directional
instability such as understeer or oversteer. Braking force is influenced by several factors, such as road and
tire conditions, coefficient of friction, etc. Unlike the conventional braking
system, in the ABS, the wheels are kept from being locked with a certain slip
state where the coefficient of adhesion between the road and the tires is the
greatest. This makes the braking distance shorter, and the vehicle remains
stable or easy to control. Therefore, cars with ABS have the ability to reduce
the stopping distance and increase maneuverability compared to those without
this system (Fernandez et al., 2021; Aksjonov, Augsburg, and Vodovozov, 2016; Aly et al.,
2011).
This process
significantly increases a vehicle's safety in extreme conditions due to its
ability to maximize tire-road friction while maintaining a large lateral
(directional) force that ensures its control (Reif,
2014; Oleksowicz et al., 2013; Sergio
and Mara, 2010). According to Kim and Lee
(2013), an optimum slip ratio value maximizes the coefficient of
friction in all road conditions. Therefore, a suitable control strategy is to
maintain the slip ratio value to ensure the braking system's optimal and safe
working range.
Designing
an anti-lock braking system is a fairly complicated design process. Here, one
of the main obstacles is in determining the nonlinearity and uncertainty. Some advanced control
approaches have been proposed for ABS, such as fuzzy (Berouaken
and Boulahia, 2015; Yazicioglu and Unlusoy, 2008; Mirzaei et al., 2005), fuzzy-neural
(Lin and Le, 2017; Wang, Chen, and Su, 2012; Chen at al., 2006), sliding mode (Guo, Jian, and
Lin,
2014; Guo and Wang, 2012), model predictive control (He et al., 2021; Yuan et al., 2015), and other intelligent controls (Mirzaeinejad, 2018; Boopathi and Abudhahir, 2016; Topalov
et al., 2011).
The use of
regenerative braking as ABS was proposed by Tur, Ustun, and
Tuncay
(2007). Simulation comparisons between ABS with
motor and hydraulic braking torques were also carried out in this research.
Next, the analysis of the combination of the regenerative braking system and
ABS is carried out (Bera, Bhattacharyya, and Samantaray, 2011) using the sliding mode controller approach. This combination is
one of the innovative technological processes to improve vehicle performance.
The combined braking also serves to avoid overvoltage problems in electric
vehicles as discussed in Yusivar et al.
(2015). However, research on the combination of the two braking torques
is still small especially when it comes to ABS.
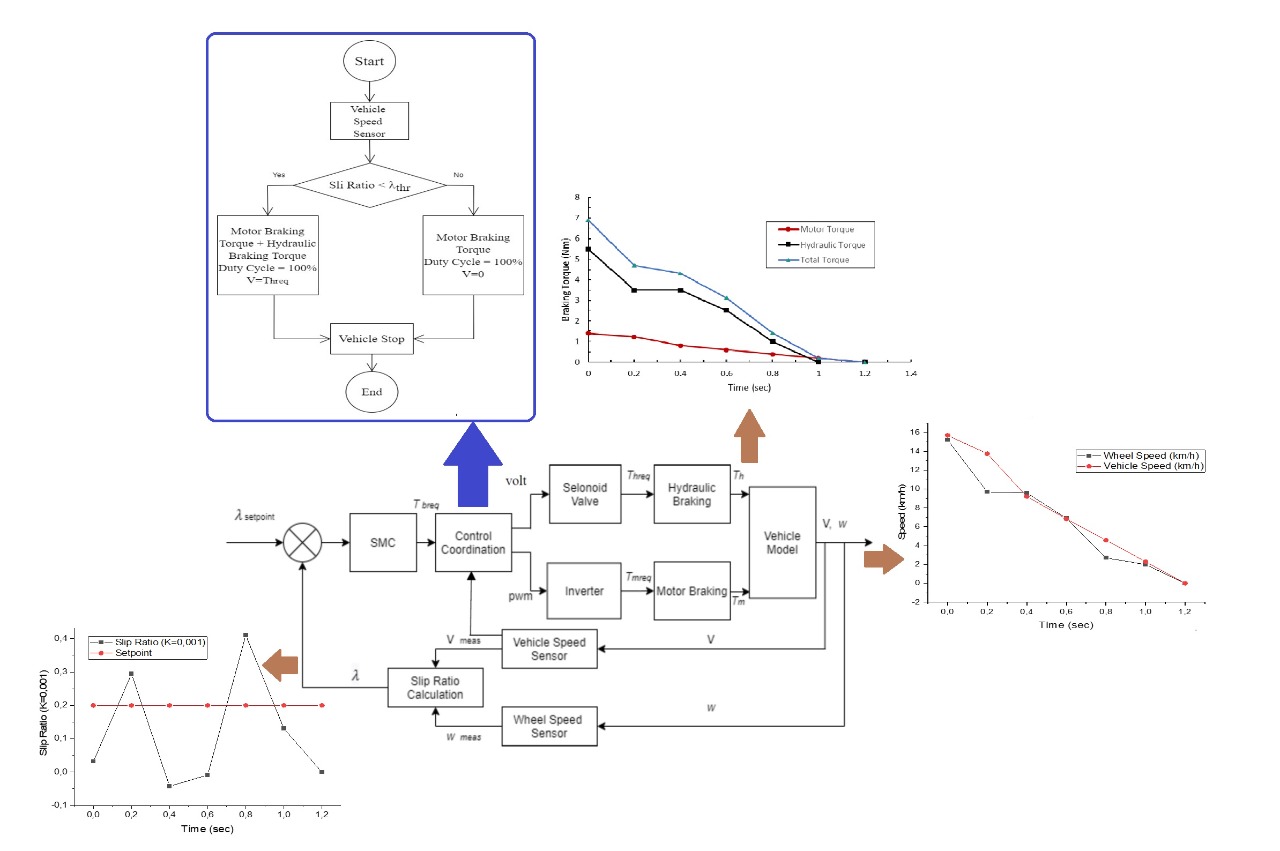
Regenerative ABS Plant
The Regenerative
Anti-lock Braking System (ABS) Plant in this research is applied to a single-wheel electric vehicle model, which only
uses one-wheel representation. The top represents the wheel speed
connected to a hydraulic braking system. Meanwhile, the bottom denotes the
vehicle's speed and is connected to a Brushless Direct
Current (BLDC) motor driver. The scheme of the regenerative ABS plant carried out in
this research is shown in Figure 1.
Figure 1
Schematic of the regenerative ABS plant (a) and the setup of the
plant (b)
This plant consists of a
battery that functions as a voltage source used by a motor driver to turn on
and regulate the vehicle. Therefore, electrical braking occurs when the driver
regulates the stator current, thereby producing attractive and repulsive forces
on the BLDC. Furthermore, this process is used to drive the bottom and top
wheels, usually zero at the point of contact. Generally, the braking system
with hydraulic torque occurs in vehicles by stopping the top wheels using brake
calipers, which decreases speed until they stop turning. In this case, a
hydraulic modulator is used to regulate the duration of braking. When a driver
applies the brake to a vehicle, the microcontroller receives speed data and
reacts to the braking module. The control algorithm used is a sliding mode
control (SMC) approach. The top and bottom wheel speed response graphs are
shown on the monitor screen.
The hydraulic modulator
consists of two on-off solenoid valves and one pump. The solenoid valve works
in reverse condition, depending on which operating position is needed as
described in Budiono et al. (2020).
However, during non-braking conditions, the input valve is closed while the
output is opened. This means that the system becomes dumped, thereby trapping
the brake fluid. Conversely, when braking is required, the output valve closes,
and the input valve opens enabling the flow of brake fluid into the calipers
and stopping the wheels. The pump is used to replace the function of the brake
pedal in every operating condition.
When brakes are applied, the BLDC changes its function from a motor to a generator. The specifications of the motor used in this research are shown in Table 1. This regenerative process reverses the current in the motor-battery circuit during deceleration and directs it to the battery. This condition is measured by the estimated state of charge (SOC) value. Therefore, it is necessary to measure Vuse, the value of the battery voltage when in use, using the equation (1):
where Vfull is the voltage when the battery is full.
Table 1 Motor Specification
|
Item |
Value |
|
Model |
BM1418ZXF |
|
Rated Output Power |
750 W |
|
Rated Voltage |
48/60V DC |
|
Speed after Reduction |
480RPM |
|
Rated Speed |
2800RPM |
|
Full Load Current |
|
|
No Load Current |
|
|
Rated Torque/Full Torque |
2.56 N.m / 14.92 N.m |
|
Efficiency |
|
|
Gear Ratio |
1:6 |
The slip ratio value is calculated using the equation (2):
where
v is the lateral (vehicle) speed of the bottom wheel
ww is the angular speed of the top wheel
rw is the top
wheel radius at 0.275 m
The measurement module
components at this plant include a speed sensor that measures wheel and vehicle
speed, a current sensor used to determine the reverse current during regenerative
braking, and a voltage divider circuit for the battery voltage.
The speed sensor in this
system uses proximity, generating two signal conditions of high and low. The
signal is high when the sensor touches the ring, and low assuming it does not
detect the ring. Furthermore, the sensor outputs a value when the ring rotates
once. However, a signal conditioning circuit needs its rotation value to reach
a revolution per minute (rpm) before entering the microcontroller. The
proximity sensor works to read the angular speed value w (rpm) on the top and bottom wheels
(vehicle representation). At the bottom, the angular speed value is converted
to the lateral v (km/h) with the equation (3):
where D is the diameter of the bottom wheel at 0.32 m.
A voltage divider circuit
is used on the battery-microcontroller line to measure the battery voltage.
This is necessary because the total voltage on the battery is around 50 Volts,
while the microcontroller's analog input pin is only capable of reading a
maximum of 5 Volts. The voltage divider circuit used in this plant uses 2
resistors of 10K and 100K Ohms at 5% tolerance, respectively.
Current measurement is carried out using an integrated circuit (IC) which detects AC and DC. This sensor works according to the Hall Effect theory, where a conductor is positioned close to the IC to create a magnetic field, converted into a proportional voltage. This analog voltage is read by the microcontroller and converted to a current value in amperes.
Regenerative ABS Control System
3.1. Sliding
Mode Control Approach
This research created a closed-loop
system for a regenerative ABS plant (Figure 2) using a sliding mode control
(SMC) suitable for plants with high nonlinearity characteristics such as ABS.
In this case, the controlled variable is the slip ratio l, which can be
calculated using the measured speed value of the vehicle (Vmeas)
or the wheel (wmeas). Therefore, it has the ability to
overcome the locked wheels when braking. The control
system is expected to set the slip ratio response around the setpoint value lsetpoint of 0.2,
which is the optimum value for dry and straight asphalt road conditions (Guo
and Wang, 2012).
The control signal with the SMC algorithm is generated using the nonlinear equation (4):
where:
Jw is the inertia moment of the wheel at 1 Nm
Kp is the proportional gain
K is controller gain
s = sliding surface = setpoint error (slip
ratio error)
The signum (sign) function is defined using (5):
The
SMC result is a control signal that represents the required braking torque, Tbreq.
The motor braking torque in this research is carried out
in full power from start to finish using a PWM signal with a duty
cycle of 100%. Therefore, continuous and discrete braking actions
are performed to produce motor and hydraulic (friction) braking torques.
The required motor braking torque Tmreq is computed using a linear function of sliding surface as (6):
Meanwhile, the hydraulic braking torque required Threq is the second-term part of (4), namely (7):
The
controller gain values Kp and K from the
SMC algorithm are determined by trial and error.
The control system adjusts the solenoid valve, which functions as an actuator to the control signal (volt). In its application, the hydraulic braking torque control signal is represented in the form of a delay. The ABS valve is controlled by 2 types of solenoids, which open and close the diaphragm to provide and relieve pressure on the brake chamber. As stated earlier, the first solenoid opens when braking and closes when the reverse is the case. Meanwhile, the second solenoid closes when braking and vice versa. Therefore, the required hydraulic braking torque is embodied in the form of braking duration or the microcontroller language using the term delay, namely (8):
where Thmax
is the hydraulic torque at maximum speed and Ts is
the sampling time.
The controller uses switching operations on the inverter. During the braking process, the inverter is tasked with increasing the back electromotive force (BEMF) voltage for current to flow into the battery. The braking energy is then stored in the battery, while the proportional control method is used to control the PWM signal on the inverter. Furthermore, the proposed system is very simple and efficient because it uses a switching operation on the inverter hence it does not require additional electronic components to perform regenerative braking.
Figure 2 Block diagram of the
slip ratio control system with SMC
3.2. Control Coordination
In an effort to obtain
regenerative energy in the motor braking section, it is necessary to regulate
the braking torque distribution. This distribution algorithm is expected to
make braking time faster with significant regenerative energy. In this
research, the distribution of braking (control coordination) is designed based
on the threshold value of the slip ratio, lthr. When it
is smaller than lthr, the
braking torque that works is hydraulic and motor. However, when the slip ratio
is greater than lthr, only
the motor works. The braking distribution then allows the torque to run from
start to finish but regulates the stopping time of the hydraulic because it
causes locked wheels. Furthermore, a controller is needed for the proper
functioning of the hydraulic braking torque to prevent slippage. In this case,
the controller algorithm used is SMC and the control coordination is able to
stop the vehicle quickly and without slipping. The braking distribution
algorithm is shown in Figure 3. lthr is
selected based on the open-loop test results of combined regenerative braking
(motor and hydraulic torque). The largest slip ratio value that occurs just
before the slip is used to determine the lthr value.
When electro-hydraulic braking is used, here the electric braking torque is
made to work at its maximum (PWM duty cycle is 100%), and the lack of braking
torque is overcome by hydraulic braking torque. So for high speed, braking can
still be done. A more detailed explanation is given in section 4 of this paper.
The regenerative performance of the ABS control system is evaluated by the SOC value and the integral of the time-multiplied absolute value of error (ITAE) which quantitatively characterizes the deviation from the actual wheel slip ratio value from the setpoint. Other performances include braking distance, brake speed, and average deceleration.
Figure 3 The proposed braking distribution algorithm
4.1. Analysis of the Effect of Braking Torque
A plant test is carried out
until the car stops in an open loop or without involving a controller. There
were 3 braking experiments, namely electric, hydraulic, and electric-hydraulic.
The open-loop test response
results for electric and hydraulic braking experiments are shown in Figures
4(a) and 4(b), i.e. slip ratio value and speed, respectively. The result
indicates that hydraulic braking with constant torque (5.5 Nm) produces a more
significant effect than the motor, as shown in Figure 5(a). Therefore, at 0.6 seconds, the system with hydraulic braking only
locks the wheels (zero speed) with a slip ratio value of 1 and the vehicle
stops at 1.2 seconds. Meanwhile, motor braking causes the vehicle to stop
at 1.6 seconds without slip events because the ratio is around ±0.2.
The regenerative energy
generated from the motor braking experiment increases the SOC value, as shown
in Figure 5(b). At the beginning of the braking process, the SOC value,
originally at 86.4%, increases until the wheel stops at 90.3%. Therefore, the
SOC value of the battery is increased by 3.9%.
Based on this experiment, it can be concluded that the slip event occurs due to the hydraulic braking torque, which needs to be adjusted without causing the wheels to lock.
Figure 4 Slip
ratio response (a) and speed response (b) during open-loop plant test with hydraulic
or motor braking
Figure 5 Braking
torque during individual tests (a) and SOC increase in the case of motor
braking torque (b)
The open-loop test response results for
the electric-hydraulic combined braking experiment are shown in Figures 6(a)
for slip ratio value and (b) for speed. The combined braking torque causes the
wheels to lock at 0.6 seconds, which is similar to the application of hydraulic
braking torque. However, the combined process causes the braking time to be
faster. In conclusion, the addition of motor braking torque accelerates the
braking time without changing the slip condition. Furthermore, the motor
braking needs to be carried out with the maximum motor braking torque to make
the maximum possible regenerative energy. Therefore, a braking distribution
algorithm is needed to regulate the regenerative energy storage without causing
slippage.
The threshold value for
distributing braking lthr is
determined based on the results of the slip ratio response in Figure 6(a). Its
value of 0.58 is obtained at 0.4 seconds just before the wheels are locked.
Therefore, the slip ratio threshold must be below this value. The braking
distribution algorithm applied in this research uses the lthr = 0.4.
Figure 6 Slip
ratio (a) and speed response (b) during the open-loop plant test
4.2. Control System Response Result
The required motor torque
value in Equation (6) is proportional to the setpoint error deviation value,
with a controller gain Kp of 13. However, this value cannot
be fulfilled entirely due to several factors influencing the motor torque. In
this case, the motor braking torque is proportional to the motor speed and the
hydraulic braking torque is equal to the required value, which is calculated by
equation (7). Based on the experimental results, it is found that the best
controller K gain value is 0.001.
The braking distribution algorithm works based on the slip ratio value, which uses the value of lthr = 0.4 as described in the previous section. The braking distribution graph shown in Figure 7 indicates that the hydraulic braking torque is no longer constant and reduces with a decrease in speed. The vehicle stops at 1.2 seconds (Figure 8(a)). At the time of 1 second, only the braking torque of the motor works because the slip ratio in the 0.8 seconds has already passed lthr, as shown in Figure 8(b). In total, the braking torque initially reached 7 N.m, however, it decreased until at 0.6 seconds to reach 3.1 N.m, therefore causing the wheels to unlock as in the case of braking with constant hydraulic torque (without controller). In this case, no more slip events occur, and the ratio value is maintained around 0.2 as shown in Figure 8(b).
Figure 7
Distribution of braking torque of the regenerative ABS control system
Figure 8 Speed response (a) and slip ratio response (b) of the regenerative ABS control system
Figure 9 SOC
value (a) and current value (b) of regenerative ABS control system
Figure 9(a) shows the changes in SOC
values due to regenerative energy conversion. Overall, there was a 3.4%
increase in SOC from 89.61% to 93%. Therefore, the regenerative energy
generated from the regenerative ABS control system is smaller than in the case
of motor braking alone at 4.7%, as shown in Figure 5(b). This is due to the
distribution of braking torque between the motor and hydraulic torque, hence
the brake speed is increased without causing the slip.
Figure 9(b) shows the
response of the motor current during braking at 3.26 A. Furthermore, when the
motor brakes, the current value changes to -0.08 A, thereby indicating that the
current direction is no longer to the motor but to the battery. This indicates
the conversion of mechanical energy with a torque value of 1.38 N.m into the
electrical current of 3.34 A, at the beginning of the braking process. The
regenerative energy generated is then significantly reduced as the speed
decreases, with a current below 0.25 A.
The regenerative ABS
control system is expected to make non-slip braking run quickly with the
maximum possible generation of regenerative energy. When the lthr value
used is less than 0.4, the braking time becomes longer, and the regenerative
energy is greater. Meanwhile, when the lthr value is
greater, the braking time becomes faster with smaller regenerative energy.
Therefore, it can be concluded that there is a trade-off between braking speed
and energy recovered. This led to the process of optimizing problems associated
with the lthr variable,
which is interesting to be used as a topic for further research.
The ABS regenerative
control system using the SMC approach is compared to its performance with the
proportional gain scheduling approach which is also conducted in this research. The
results of the performance comparison are shown in Table 2. It shows that the
SMC approach is slightly superior in all aspects, including ITAE. Thus, it can
be concluded that the type of nonlinear control algorithm is not the main
determinant for the performance of the combined braking system, but it is the
coordination control that determines the performance of the regenerative ABS.
Table 2
Comparison of Control Scheme Performance
|
No |
Scheme |
Average Deceleration (m/s2) |
Braking Distance (m) |
ITAE |
SOC (%) |
Brake Speed (m/s) |
|
1 |
SMC |
0.726 |
2.473 |
0.719 |
3.39 % |
2.025 |
|
2 |
Proportional
Gain Scheduling |
0.63 |
2.38 |
0.71 |
2.43 % |
1.983 |
In
conclusion, the regenerative ABS control system equipped with a braking
distribution feature has the ability to produce fast non-slip braking action
and increase the battery SOC by almost 4%. The continuous action of the motor
braking torque plays a role in accelerating the braking time in addition to
generating regenerative energy. Meanwhile, the discrete action of hydraulic
braking torque plays a role in accelerating braking time and needs to be
limited to avoid slipping through coordinated control based on the threshold
value of the slip ratio. Therefore, the process of determining this threshold
value can be used as a topic for future research to achieve optimum
regenerative braking conditions.
The authors are grateful to the Institut Teknologi Sepuluh Nopember for
their financial support under the Collaboration Research Centre project scheme
(reference
1159/PKS/ITS/2021).
Aly, A.A., Zeidan,
E.S., Hamed, A., Salem, F., 2011. An Antilock-Braking Systems (ABS) Control: A Technical
Review. Intelligent control and Automation. Volume 2(03), pp. 186
Aksjonov, A., Augsburg,
K., Vodovozov, V., 2016. Design and Simulation of The Robust ABS and ESP Fuzzy
Logic Controller on The Complex Braking Maneuvers. Applied Sciences, Volume 6(12), p. 382
Bera, T.K.,
Bhattacharyya, K., Samantaray, A.K., 2011. Bond Graph Model-Based Evaluation of
a Sliding Mode Controller for Combined Regenerative and Antilock Braking System.
Part I Journal System Control Engineering, Volume 225, pp. 918–934
Benetti, G., Delfanti,
M., Facchinetti, T., Falabretti, D., Merlo, M., 2014. Real-Time Modeling and
Control Of Electric Vehicles Charging Processes. IEEE Transactions on Smart Grid, 6(3), pp. 1375–1385
Berouaken, A., Boulahia,
R., 2015. Fuzzy Control of Anti-Lock Braking System And Active Suspension In A
Vehicle. Sciences & Technologie.
B, Sciences de l'ingénieur, Volume 2015, pp. 41–45
Boopathi, A.M.,
Abudhahir, A., 2016. Adaptive Fuzzy Sliding Mode Controller for Wheel Slip
Control in Antilock Braking System. Journal
of Engineering Research, Volume 4, pp. 1–19
Budiono, H.D.S.,
Sumarsono, D.A., Adhitya, M., Baskoro, A.S., Saragih, A.S., Prasetya, S.,
Zainuri, F., Nazaruddin, Heryana, G., Siregar, R., 2020. Development of Smart
Magnetic Braking Actuator Control for A Heavy Electric Vehicle. International
Journal of Technology, Volume 11(7), pp. 1337–1347
Chen, G.M., Wang, W.Y.,
Lee, T.T., Tao, C.W., 2006. Observer-Based Direct Adaptive Fuzzy-Neural Control
for Anti-lock Braking Systems. International
Journal of Fuzzy Systems, 8(4).
Faria, M., Delgado,
2014. Managing The Charging of Electrical Vehicle: Impacts on The Electrical
Grid and on The Environmental. Intelligent Transportation Systems Magazine
IEEE, Volume 6(3), pp. 54–65
Fernández, J.P.,
Vargas, M.A., García, J.M.V., Carrillo, J.A.C., Aguilar, J.J.C., 2021.
Coevolutionary Optimization of A Fuzzy Logic Controller For Antilock Braking
Systems Under Changing Road Conditions. IEEE
Transactions on Vehicular Technology, Volume 70(2), pp. 1255–1268
Guo, J., Jian, X., Lin,
G., 2014. Performance Evaluation of an Anti-Lock Braking System for Electric
Vehicles with a Fuzzy Sliding Mode Controller. Energies, Volume 7(10),
pp. 6459–6476
Guo, J., Wang, J.,
2012. Application of Sliding Mode Control for Electric Vehicle Antilock Braking
Systems. Advanced
Materials Research, Volume 505, pp. 440–446
He, Z., Shi, Q., Wei,
Y., Gao, B., Zhu, B., He, L., 2021. A Model Predictive Control Approach with
Slip Ratio Estimation for Electric Motor Anti-Lock Braking of Battery Electric
Vehicle. IEEE Transactions on Industrial
Electronics, Volume 69(9), pp. 9225–9234
Kim, J., Lee, J., 2013.
Real-Time Estimation of Maximum Friction and Optimal Slip Ratio Based on
Material Identification for a Mobile Robot on Rough Terrain. In: 13th International
Conference on Control, Automation and Systems (ICCAS 2013), pp. 1708–1713
Li, W., Du, H., Li, W.,
2016. A New Torque Distribution Strategy for Blended Anti-Lock Braking Systems
of Electric Vehicles Based On Road Conditions And Driver's Intentions. SAE International Journal of Passenger
Cars-Mechanical Systems, Volume 9, pp. 107–115
Lin, C.M., Le, T.L.,
2017. PSO-Self-Organizing Interval Type-2 Fuzzy Neural Network for Antilock
Braking Systems. International Journal of
Fuzzy Systems, Volume 19, pp. 1362–1374
Mirzaei, A., Moallem, M., Mirzaeian, B.,
Fahimi, B., 2005, September. Design of an Optimal Fuzzy Controller For Antilock
Braking Systems. In 2005 IEEE Vehicle
Power and Propulsion Conference, pp. 823–828
Mirzaeinejad, H., 2018. Robust Predictive
Control of Wheel Slip in Antilock Braking Systems Based On Radial Basis
Function Neural Network. Applied Soft
Computing, Volume 70, pp. 318–329
Nugraha, A.A., Sumarsono, D.A., Adhitya, M.,
Prasetya, S., 2021. Development of Brake Booster Design for Electric City Cars. International
Journal of Technology. Volume 12(4), pp. 802–812
Oleksowicz, S.A.,
Burnham, K.J., Southgate, A., McCoy, C., Waite, G., Hardwick, G., Harrington, C., McMurran, R., 2013. Regenerative Braking
Strategies, Vehicle Safety and Stability Control Systems: Critical Use-Case
Proposals. Vehicle System Dynamics, Volume
51(5), pp. 684–699
Rajendran, S.,
Spurgeon, S., Tsampardoukas, G., Hampson, R., 2018. Intelligent Sliding Mode
Scheme For Regenerative Braking Control. IFAC-PapersOnLine,
Volume 51(25), pp. 334–339
Reif, K., 2014. Brakes, Brake Control and Driver Assistance
Systems. Weisbaden, Germany, Springer Vieweg
Sergio, M.S., Mara, T.,
2010. Active Braking Control Systems Design for Vehicles. London, UK:
Springer.
Shah, D.A., Yu, L.,
Liu, X., Zheng, S., 2018. A New Design Of Main Cylinder Electric Booster For
Brake-By-Wire System. In: International Design Engineering Technical
Conferences and Computers and Information in Engineering Conference, Volume
2018, p. 85570
Tehrani, M.M.,
Hairi-Yazdi, R., Haghpanah-Jahromi, B., Esfahanian, V., Amiri, M., Jafari, R.
2011. Design of an Anti-Lock Regenerative Braking System for A Series Hybrid
Electric Vehicle. International Journal
of Automotive Engineering, Volume 1(2), pp. 16-20.
Topalov, A., Oniz, Y.,
Kayacan, E., Kaynak, O., 2011. Neuro-fuzzy Control of Antilock Braking System
Using Sliding Mode Incremental Learning Algorithm. Neurocomputing, Volume
74(11), pp. 1883–1893
Tur, O., Ustun, O., Tuncay, R.N., 2007.
An Introduction to Regenerative Braking of Electric Vehicles as ABS. In: IEEE Intelligent Vehicles Symposium, Volume
2017, pp. 944–948
Usman, M., Knapen, L., Vanrompay, Y.,
Bellemans, T., Janssens, D., Wets, G., 2016. A Coordinated Framework for
Optimized Charging of EV Fleet in Smart Grid. Procedia Computer Science, Volume 94, pp. 332–339
Wang, W.Y., Chen, M.C., Su, S.F., 2012.
Hierarchical T–S Fuzzy-Neural Control of Anti-Lock Braking System and Active
Suspension in a Vehicle. Automatica, Volume 48(8), pp. 1698–1706
Yazicioglu, Y.,
Unlusoy, Y.S., 2008. A Fuzzy Logic Controlled Anti-Lock Braking System (ABS)
For Improved Braking Performance and Directional Stability. International Journal of Vehicle Design,
Volume 48(3-4), pp. 299–315
Yuan, L., Chen, H.,
Ren, B., Zhao, H., 2015. Model Predictive Slip Control for Electric Vehicle
With Four In-Wheel Motors. In: 34th Chinese Control
Conference (CCC), Volume 2015, pp. 7895-7900
Yusivar, F., Haslim,
H.S., Farabi, Y., Nuryadi, K., 2015. New Control Scheme for Combined
Regenerative and Mechanical Brakes in Electric Vehicles. International
Journal of Technology, Volume 6(1), pp. 44–52
Yu,
L., Liu, X., Liu, X., 2016. Analysis of Energy Consumption on Typical
Main Cylinder Booster Based Brake-by-Wire System (No. 2016-01-1955). SAE Technical Paper, Volume 2016
Zhang, J.L., Yin,
C.L., Zhang, J.W., 2010. Improvement Of Drivability and Fuel Economy With A Hybrid
Antiskid Braking System In Hybrid Electric Vehicles. International Journal
Of Automotive Technology, Volume 11(2), pp. 205–213
