Modification of Horizontal Wind Turbine Blade: A Finite Element Analysis
Corresponding email: milad@gcet.edu.om
Published at : 18 Jan 2023
Volume : IJtech
Vol 14, No 1 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i1.5255
Hamza, S., Heidari, M., Ahmadizadeh, M., Dashtizadeh, M., Chitt, M., 2023. Modification of Horizontal Wind Turbine Blade: A Finite Element Analysis. International Journal of Technology. Volume 14(1), pp. 5-14
| Sahahd Hamza | Mechanical Engineering Department, Global College of Engineering and Technology, P.O. Box 2546,CPO Ruwi 112, Muscat, Sultanate of Oman |
| Milad Heidari | Mechanical Engineering Department, Global College of Engineering and Technology, P.O. Box 2546,CPO Ruwi 112, Muscat, Sultanate of Oman |
| Mohammad Ahmadizadeh | Department of Mechanical Engineering, Faculty of Engineering, Persian Gulf University, P.C. 7516913817, Bushehr, Iran |
| Mohammadreza Dashtizadeh | Department of Mechanical Engineering, Faculty of Engineering, Shiraz Branch, Islamic Azad University, Sadra, Shiraz, Iran |
| Mira Chitt | Mechanical Engineering Department, Global College of Engineering and Technology, P.O. Box 2546,CPO Ruwi 112, Muscat, Sultanate of Oman |
Turbines are efficient power generators.
Because wind energy is a clean fuel source, it is widely utilized in some
regions. One of the major factors affecting wind turbine performance is the
angle of attack of the blade. The aerodynamics and efficiency can be improved
by improvising the lift-to-drag ratio CL/CD to get the best design for wind
turbine blades. There are many factors affecting the efficiency of horizontal
wind turbine blades such as the angle of attack of the blade. Therefore, this
study investigated the effect of the angle of attack on coefficients and
forces, particularly on a blade with NACA 4412 airfoil in a horizontal axis
wind turbine. The length, thickness, and chord length of the blade were 3m,
0.36m, and 0.12 m
respectively. Computational Fluid Dynamics was used to develop to obtain lift
and drag coefficients in a horizontal wind turbine blade. In addition, the correlation between
different angles of attack, lift, and drag forces were studied and validated.
The results demonstrated that the lift and drag coefficients increase as the
angle of attack increases. Furthermore, the optimal angle of attack for this
study was 0° because it has the highest lift-to-drag ratio, resulting in the
greatest efficiency. The results demonstrated that it is possible to have a
different lift and drag coefficient for the same angles of attack at a similar
airfoil.
Angle of attack; Energy; Horizontal wind turbine; Lift-to-drag ratio
Globally, renewable energy is now more cost-effective
than fossil fuels (Sudarsono, Susastriawan, and Sugianto, 2019). Renewable energy is of great importance nowadays. It
provides reliable power supplies and fuel diversity, which leads to energy
security and lower fuel demand. There are various renewable energy sources. The
wind is one of the elements. Horizontal-axis turbines and vertical-axis
turbines are the two main types of wind turbines. The rotating axis of a wind
turbine is horizontal, or parallel to the ground if it has a horizontal axis.
The turbine's rotational axis is vertical or perpendicular to the ground in
vertical-axis wind turbines. In comparison to the
vertical design, the horizontal one is more common as it produces more power,
causing it the most common machine design in use today.
The blade is designed as an aerodynamic geometry with
nonlinear chord and twist angle distributions to convert wind energy into
mechanical power (Tang, 2012). Because numerous disciplines are involved, such as aerodynamics,
construction, materials, and economics, wind turbine blade design is a
multi-objective optimization process. The three main models that represent the
design process are an aerodynamic model, a structural model, and an economic
model (cost model). These three elements form the foundation of wind turbine
design. The aerodynamics model is crucial in the design of wind turbine rotor
blades and other components. Furthermore, the initial concern in the wind
turbine design process is an accurate aerodynamic model. The structural design
of a wind turbine blade includes defining the wind turbine loads, selecting an
appropriate material, building a structural model, and solving the model using
the finite element method. This process will be repeated several times until a
final design is achieved (Kasem, 2020). Cost of materials, labor and cycle durations, and
virtual factory are the three key processes that make up the cost model for
horizontal wind turbines.
First, the bill cost of materials is estimated, then labor and cycle
time for a vacuum-assisted resin transfer molding process. This data is used to
create a virtual blade. It calculates the costs per blade for labor, utilities,
buildings, tools, equipment, maintenance, overhead, and capital. (Bortolotti et al., 2019).
Based on blade element momentum theory, Chaudhary and Roy (2015) reported on
the design and optimization of rotor blade performance for a 400-W compact wind
turbine at lower operating wind speeds (BEM). The main focus was the link
between solidity, pitch angle, tip speed ratio, and maximum power coefficient.
For a number of blades of 3, 5, and 7, the maximum power coefficient was found
for solidity in the range of 3% to 12% (Chaudhary and Roy, 2015). Yavuz et al. conducted an in-depth analysis of wind turbine
blades' design and performance evaluation and the outcome (Yavuz et al., 2015). Turbines are
efficient power generators. The turbine will not operate and produce power
efficiently if the speed is lower than the range. According to Yavuz et al.,
the greatest lift coefficient occurs when the attack angle is approximately 12
°, and the minimum velocity required to generate power is calculated to be 7
m/s (Yavuz
et al., 2015). Chang et al. devised a method that
incorporates design goals such as airfoil lift, drag coefficients, and
lift-drag ratio to produce an analytical expression that results in a highly
smooth airfoil for wind turbine applications. According to the study, airfoils
created using the proposed technology showed delayed flow separation and
excellent airfoil performance (Chang, et al., 2014).
Additionally,
Johansen et al. also developed a three-blade wind turbine rotor design
that maximizes the mechanical power coefficient (CP) in operating
circumstances. A free-wake lifting line approach and a three-dimensional
Navier-Stokes Solver were utilized to validate the model, which was created
using an actuator disc. The study found that CP = 0.51 and that it grows and
reduces as you get closer to the root and tip (Johansen et al., 2009).
One of the most challenging aspects in assessing the efficiency of a
wind turbine blade is the drag throughout its length, which attempts to stop
its movement. Drag is caused by the friction of air against the blade surface.
It runs parallel to the lift and in the same direction as the airflow across
the blade surface. Bending or twisting the blade, as well as tapering it
throughout its length, can reduce drag, resulting in the most efficient wind
turbine blade design. To enhance the efficiency of wind turbine blades, the
rotor blades require an aerodynamic profile to create lift and rotate the
turbine (Woofenden,
2013). The angle of
attack (AOA) of an airfoil is a 2D concept defined as the
angle between its chord and the undisturbed streamlines far upstream. Furthermore, it is the variation between lift and
drags with its direction of travel through a fluid. The determination of
the angle of attack is necessary in order to calculate lift and drag forces
over the blade, develop accurate aeroelastic models, or establish a control
tool (Soto-Valle
et al., 2020).
Various factors affect the efficiency of horizontal wind turbine blades
includingthe angle of attack of the blade. The angle of attack of the blade is
one of the most dominating parameters for wind turbine control and blade design
(Wen
et al., 2018). Ravi, Madhukeshwara, and Kumarappa (2015) presented a study on
NACA 4412 airfoil to compare wind tunnel test experimental results of lift and drag coefficients with two different modeling
approaches, namely the
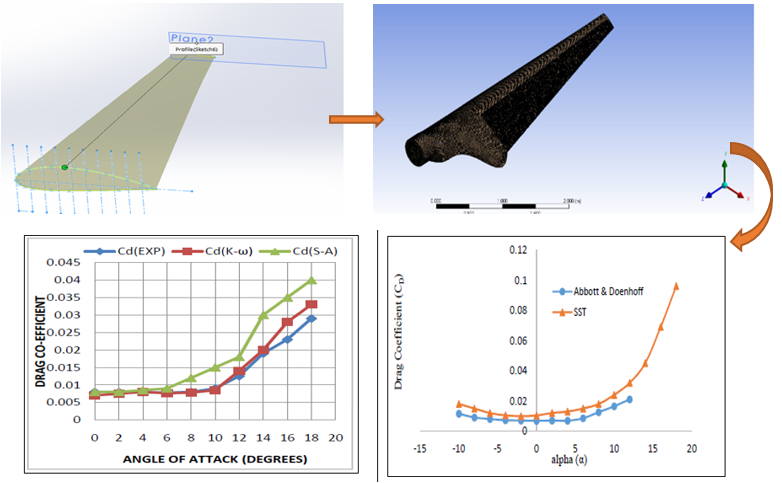
k-? model and the Spalart-Allmaras model (Ravi, Madhukeshwara, and Kumarappa, 2015). These comparisons
revealed that the two models provided close predictions of the experimental
outcomes. It is concluded that the K-? SST turbulence model with transition
capabilities gives a close prediction of lift and drag coefficient both in the
pre-stall and post-stall region.
This study investigates the effect of the angle of attack on
coefficients and forces, specifically on a blade with NACA 4412 airfoil in a
horizontal axis wind turbine. The length, thickness, and chord length of the
blade were 3m, 0.36m, and 0.12m respectively. To accomplish these objectives, a
method was developed to model the horizontal wind turbine blade, generate
meshes, and perform Computational Fluid Dynamics (CFD) of horizontal axis wind
turbine blades to find lift and drag coefficients. CFD assists in determining
whether or not the turbine can operate because, if the turbine fails in CFD, it
will probably fail empirically. In addition, the correlation between different
angles of attack, lift, and drag forces have been investigated in this study.
Lastly, an attempt was made to compare the efficiency with other results by
modeling horizontal axis wind turbine blades in real dimensions. The real-size simulation, which is suitable
for the climate of the city, can be a significant reference for comparing data
between smaller and real sizes. Due to their high complexity, air-fluid and
aerodynamic calculations can generate strange and extraordinary results in
different dimensions. This type of analysis can be useful for improving wind
turbine blades in specific cities and may assist other researchers to achieve
more accurate results.
One of the most commonly used is NACA 4412
airfoil because it has a high cl/cd ratio. (Lololau et al., 2021). For instance, the NACA 4412 wing section has a 4%
camber at 0.4 chords from the leading edge and a 12% thickness. Teak is
utilized as the blade material because of its ease of production, availability,
and affordability (Sekhar, Kumar, and Reddy, 2014). Furthermore, the use of teak wood
blades were chosen due to their light weight and ability to withstand fatigue
testing (Maldhure and Kharde, 2013). It was agreed that SolidWorks software would be
utilized for the project's modeling work.
Figure 1 depicts the forces and angles of relative wind (p) and angle of attack (a) acting on blade sections, where TN and TQ are normal (thrust) and tangential (torque) forces, respectively, and both forces are generated by lift (L) and drag (D) forces.
Figure 1 Diagram of
the angles and forces on one of the sections of the HAWT blade
The Drag force
is a rearward, retarding force caused by disruption of airflow by the wing,
rotor, fuselage, and other protruding objects. The coefficient of drag is
defined by the equation (1) below:
Where: D is the drag force, ? density of the air (kg/m3), Vr relative velocity when air flowed through the airfoil (m/s), and l is the chord length (m). The Lift force
is a force that opposes the downward force of weight. It is produced by the
dynamic effect of the air acting on the airfoil and acts perpendicular to the
flightpath through the center of the lift. The
coefficient of lift is defined by following equation:
Where: L is the drag force, ? density of the air (kg/m3), Vr relative velocity when air flowed through the airfoil (m/s), and l is the chord length (m).
In this study,
the modeling process was initiated by creating the blade curve at the front
plane using (curves through xyz points) from the Curves menu from the Features
panel. As a reference for the blade length, the front plane was 3 m away from
the original curve and 0.36 m thick, while the chord length was 0.12 m. The
airfoil curves are then converted to a sketch on their respective reference
planes and twisted about their aerodynamic center. The new plane was used to
scale the original curve into a smaller entity with a ratio of 0.26 smaller
than the original curve. The scaled entity was given a 10-degree twist in the
direction denoted by the negative sign, which refers to the direction of the
twist. Additionally, a lofted base boss was made between the two planes which
consist of the original curve and the scaled entity, as depicted in Figure 2.
After lofting the two planes, a new sketch was created using the front plane to
draw a 250 mm-diameter circle and a construction line at the first quarter of
the chord length. Moreover, a new sketch was created at the front plane by
drawing a line connecting the blade and the circle. At the right side of the
blade, a spline was sketched to shape the blade.
Figure 2 Left: Lofted Boss Base; Right: The CAD model
after meshing
A horizontal-axis wind turbine blade with a Naca 4412 airfoil was
modeled and analyzed in this study. The blade measured 3 meters in length, 0.36
meters in thickness, and 0.12 meters in chord length. The blade was analyzed in
the simulated wind tunnel using Ansys software. The blade was placed horizontally
and connected to the left wall from the root in the direction of the X-axis in
the mentioned wind tunnel; it was located at the end of the first third of the
wind tunnel. The entrance surface of the tunnel had a curved projection. Hence,
the wind entering the tunnel would be proportional to its speed, Reynolds
number, and disturbances. The X-axis or transverse axis of the wind tunnel
should be used when adjusting the angle of attack. This angular change was done
without displacement in the depth of the wind tunnel. The depth of the wind
tunnel was three times the length of the blade. Air entered the blade from the
front of the wind tunnel at a speed of 6.9 m/s. In this study, the Reynolds
number was determined based on the kinematic viscosity value which is
The mesh
generating process was conducted using ANSYS Workbench Project Schematic and double-click on the Mesh cell in the elbow fluid flows analysis
system as shown in Figure 2. Generating a mesh manually can be
time-consuming and error-prone. Mesh size is a key factor in an effective
simulation. Mesh refining techniques should be used to optimize mesh
sensitivity to produce a mesh of excellent quality. Mesh convergence was done
in this study. A blade was modeled and meshed with eight different sizes
ranging from 0.5 mm to 5.5 mm. Both lift and drag were obtained. It was
observed that the outcomes are approximately the same with a 2-mm mesh size.
Hence, convergence was reached when there was no qualitative change in the
result of less than 1% in the blade. Therefore, a mesh size of 2 mm was chosen
for the whole study.
Despite the fact that ANSYS CFD is an industry-standard modeling software, it is important to ensure that the results produced are logical and valid. The results produced from the blade using ANSYS were compared with XFLR5 software. XFLR5 is a user-friendly design and analysis program for airfoils and bodies. The program analyzes the aerodynamic performance of two-dimensional airfoils using XFOIL codes. The program is capable of calculating lift, drag, pitching moment, and pressure coefficients of airfoils in two-dimension by using a fully coupled viscous/non viscous interaction method with a high-order panel method (GÜZELBEY, Eraslan and Dogru, 2018). The results obtained from ANSYS Fluent were compared with XFLR5 software to guarantee the accuracy of the results.
Several parameters influence
the efficiency of horizontal wind turbine blades, including the blade's angle
of attack. One of the most important criteria for wind turbine control and
blade design is the angle of attack of the blade (Wen et al.,
2018). The effect of the angle of attack on lift and drag
coefficients and forces of NACA 4412 is studied insufficiently. This research
will investigate this correlation to increase the efficiency of horizontal
wind turbines. Therefore,, the focus of this research is on the alteration of
horizontal wind turbine blades. To accomplish these goals, a methodology for
modeling a horizontal wind turbine blade, creating meshes, and performing
computations were created.
Figure 3 compares the outcomes of previous studies
conducted to determine the lift coefficient for NACA 4412 with the outcomes of
the current study. Figures 3.1, 3.2, and 3.3 are the results of the previous
studies conducted on the relation between the angle of attack and lift
coefficient, while Figure 3.4 is the result of the current study. In all
the studies, the lift coefficient is observed to increases as the angle of
attack increases. Also observed in the previous study is that after 16°, the
lift coefficient starts to decrease as the blade stalls, and the lift decreases
once more. Nevertheless, the results of the present study indicated that the
lift coefficient continued to increase until it reached 20°.
Figure
3 Comparison between different graphs to obtain Cl;
(a): Ravi, Madhukeshwara, and Kumarappa, (b): Petinrin and Onoja, (c): Khaled,
(d): current study.
The results
obtained from this study were relatively similar to the results of previous
studies conducted to find the drag coefficient. Table 1 displays the results of
a study conducted by Ravi utilizing the book “theory of wing sections” by
Abbott with two different modeling approaches, namely the k-? model and
Spalart-Allmaras, and the results of the current study from 0°-18°.
This indicates that the Spalart-Allmaras has the highest matching with the current
study results of Cd.
Figure 4 shows a comparison between the results from the previous
studies conducted to find the drag coefficient for NACA 4412 in addition to the
results obtained from this study. It is observed that in all the studies the
drag coefficient increases with the increase in the angle of attack. Also, the
drag coefficient starts to decrease after 16°. However, the
results obtained from this study indicated that the lift coefficient kept
increasing until 20°.
Table 1 Comparison
between Ravi, Madhukeshwara, and Kumarappa’s study to obtain Cd
|
AOA |
Current Cd
Results |
Spalart-Allmaras Cd results |
K-? model Cd
results |
Wind Tunnel
Test Cd results |
|
0 |
0.005 |
0.008 |
0.007 |
0.008 |
|
2 |
0.01 |
0.008 |
0.0075 |
0.008 |
|
4 |
0.017 |
0.0085 |
0.008 |
0.0079 |
|
6 |
0.026 |
0.009 |
0.0076 |
0.0078 |
|
8 |
0.037 |
0.012 |
0.0078 |
0.008 |
|
10 |
0.049 |
0.015 |
0.0085 |
0.009 |
|
12 |
0.062 |
0.018 |
0.014 |
0.0125 |
|
14 |
0.077 |
0.03 |
0.02 |
0.019 |
|
16 |
0.092 |
0.035 |
0.028 |
0.023 |
|
18 |
0.109 |
0.04 |
0.033 |
0.029 |
Figure 4 Comparison between different graphs to obtain Cd; (a): Ravi, Madhukeshwara, and Kumarappa, (b): Petinrin and Onoja, (c): Khaled study, (d): the current study
Figure 5 shows a comparison between the results from the previous studies conducted to find a lift-to-drag ratio for NACA 4412 in addition to the results obtained from this study. Khaled's previous research demonstrated that the efficient attack angle for an airfoil is 6 °, after which the efficiency of the airfoil decreases. The current study indicated that the most efficient attack angle is 0°. This experiment was conducted at angles ranging from -14° to 20°. The expectations for angles above 20° are likely to have an increment in lift force and drag force. Consequently, both the lift and drag coefficients will rise.
Figure 5 Comparison
between different graphs to obtain
Cl/Cd; (a): Khaled study, (b): the current study
This
project is modifying the horizontal wind turbine blade design by studying the
effect of blade angle of attack on efficiency. In 2019, lift and drag are the
key factors affecting wind turbine efficiency. The project was conducted by
selecting an appropriate airfoil, selecting appropriate software, modeling a
horizontal wind turbine blade using SolidWorks, transferring CAD files into
Ansys, running models and investigating CFD results, and validating the
obtained results. CFD investigation was conducted on an attack angle ranging
from -14° to 20°.
The
negative lift coefficient only occurs at small angles of attack, which
corresponds to laminar separation without flow transition and reattachment. It
also implies that the lift is acting in the opposite direction of the body (Pranesh, et al, 2019). It was
determined that the lift coefficient increased as the angle of attack increased
because the angle between the chord line and relative wind increased.
Furthermore, it is also observed that the drag coefficient decreased until it
reached to 0°, then it increased as the lift coefficient increased. As
the angle of attack increases, the lift coefficient increases which affects in
the amount of the induced drag. This effect is known as “induced drag” or “drag
due to lift.” Induced drag increases as the angle of attack of the blade
increase. As a result of increasing the drag coefficient, the drag force
increased too. Positive drag force indicates that the airfoil is decelerating;
thus, the values obtained experimentally indicate that the drag is causing the wind
turbine blade to slow. Furthermore, the lift-to-drag ratio is used to express
the relation between lift and drag and is determined by dividing the lift
coefficient by the drag coefficient. This ratio indicates the airfoil’s
efficiency; the higher the ratio the more efficient is the airfoil.
The
findings of this research were close to the previous studies conducted to find
lift coefficients. In the literature, it has been demonstrated that a higher
Reynolds number results in a higher lift coefficient; thus, the difference in
lift coefficient results can be attributed to the use of various Reynolds
numbers. The current study used a Reynolds number of 563,500, whereas the
previous study used a Reynolds number of 3 million.
The angle of
attack is a significant factor that affects the efficiency of the blade.
Furthermore, it is very important to determine the ideal attack angle for the
airfoil selected to guarantee the best performance and efficiency. This project
aimed to investigate the impact of the relationship between angle attack and
efficiency by determining the optimal angle of attack to increase the
efficiency of the horizontal axis wind turbine blade. Therefore, an analysis
was conducted on the blade to find the lift coefficient, drag coefficient, and
lift and lift-to-drag coefficient ratio. Furthermore, the lift and drag force
affecting the blade was determined and calculated. This study concluded that
the most efficient attack angle for NACA 4412 is 0° and the
highest lift and drag coefficient occurred at 20°. The results
demonstrated that an identical airfoil have different lift and drag
coefficients at the same angle of attack. This study was conducted by modeling
a full blade and performing dynamic analysis on the blade to produce results,
which may cause a source of errors due to modeling errors. However, this
problem can be overcome by using an airfoil curve instead of the entire blade
for the analysis.
This research
was funded by Oman's Global College of Engineering and Technology.
Bortolotti, P., D. Berry, R. Murray, E.
Gaertner, D. Jenne, R. Damiani, G. Barter, K. Dykes. 2019. A detailed wind
turbine blade cost model. Report Golden National Renewable Energy
Laboratory, NREL/TP-5000-73585, USA
Chang, J., Zhu,W., Fischer, A., Garcla, N.R.,
Madsen, J., Chen, J., Shen,W.Z. 2014. Design and validation of the high
performance and low noise CQU-DTU-LN1 airfoils. Wind Energy, Volume 17, pp. 1817–1833
Chaudhary, M., Roy A., 2015. Design & optimization of a small wind turbine blade for operation at low wind speed, International Journal on Recent Technologies in Mechanical and Electrical Engineering, Volume 2(3), pp. 83–94
GÜZELBEY, I.H., Eraslan Y., Dogru, M.H., 2018. Numerical Investigation of Different Airfoils at Low Reynolds Number in terms of Aerodynamic Performance of Sailplanes by using XFLR5. Karadeniz Fen Bilimleri Dergisi, Volume 8(1), pp. 47–65
Johansen, J., Madsen, H.A., Gaunaa, M., Bak,
C., Srensen, N.N. 2009. Design of a wind turbine rotor for maximum aerodynamic
efficiency. Wind Energy, Volume12, pp.
261–273
Kasem, M.A.M., 2020. Aerodynamic, structural,
and aeroelastic design of wind turbine blades. In: Design
Optimization of Wind Energy Conversion Systems with Applications. IntechOpen, pp. 109–125
Lololau, A., Soemardi, T.P., Purnama, H.,
Polit, O., 2021. Composite multiaxial mechanics: laminate design optimization
of taper-less wind turbine blades with ramie fiber-reinforced polylactic acid. International
Journal of Technology, Volume 12(6), pp. 1273–1287
Maldhure, S., Kharde, D., 2013. Fatigue
failure analysis of small wooden wind turbine blade. International Journal
of Computational Engineering Research, Volume 3(2), pp. 2250–3005
Pranesh, C., Sivapragasam M., Deshpande M.D.,
Narahari H.K. 2018. Negative lift characteristics of NACA 0012 aerofoil at low
Reynolds numbers. Sådhanå, p. 44:21
Ravi, H.C., Madhukeshwara, N., Kumarappa, S.,
2013. Numerical investigation of flow transition for NACA-4412 airfoil
using computational fluid dynamics, International Journal of Innovative
Research in Science, Engineering and Technology, Volume 2(7), pp. 2778–2785
Sekhar, ?.C.K., Kumar ?.N.G., Reddy, ?.?.B.G., 2014. Design of blade for a wooden small scale
wind turbine for domestic purposes. International Journal of Current
Engineering and Technology, Volume 44(33), pp. 1309–1313
Soto-Valle, R., Bartholomay, S., Alber, J., Manolesos,
M., Nayeri, C.N., Paschereit, C.O., 2020. Determination of the angle of
attack on a research wind turbine rotor blade using surface pressure
measurements, Wind Energy Science Discussions, Volume 2020, p. 35
Sudarsono, Susastriawan, A.A., Sugianto.,
2019. Three-dimensional cfd analysis of performance of small-scale hawt based
on modified NACA-4415 airfoil. International Journal of Technology, Volume
10(1), pp. 212–221
Tang, X., 2012. Aerodynamic design
and analysis of small horizontal axis wind turbine blades. Thesis,
University of Central Lancashire, United Kingdom
Yavuz, T., Koç, E., K?lk??, B., Erol, Ö.,
Balas, C., Aydemir, T., 2015. Performance analysis of the airfoil-slat arrangements
for hydro and wind turbine applications. Renewable
Energy, Volume 74(C), pp 414-421
Wen, B., Tian, X., Dong, X., Peng, Z., Zhang,
W., Wei, K., 2019. A numerical study on the angle of attack to the
blade of a horizontal-axis offshore floating wind turbine under static and
yawed conditions. Energy, Volume 168, pp. 1138–1156
Woofenden, I.,
2013. Wind Power for Dummies, Wiley Publishing Inc
