A Novel Hybrid Spotted Hyena Optimizer: An Algorithm for Fuel Consumption Capacitated Vehicle Routing Problem
Published at : 28 Jul 2023
Volume : IJtech
Vol 14, No 5 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i5.5148
Utama, D.M., Yurifah, A., Garside, A.K., 2023. A Novel Hybrid Spotted Hyena Optimizer: An Algorithm for Fuel Consumption Capacitated Vehicle Routing Problem. International Journal of Technology. Volume 14(5), pp. 1049-1059
| Dana Marsetiya Utama | Department of Industrial Engineering, University of Muhammadiyah Malang, Jl. Tlogomas No. 246, 65144 Malang, East Java, Indonesia |
| Aminatul Yurifah | Department of Industrial Engineering, University of Muhammadiyah Malang, Jl. Tlogomas No. 246, 65144 Malang, East Java, Indonesia |
| Annisa Kesy Garside | Department of Industrial Engineering, University of Muhammadiyah Malang, Jl. Tlogomas No. 246, 65144 Malang, East Java, Indonesia |
Distribution activities are closely related to
the objective function of minimizing fuel consumption, which is affected by
distance and product load in transportation. This indicates the need for
optimization to improve company performance. Therefore, this study aims to
develop a new Hybrid Spotted Hyena Optimizer (HSHO) algorithm, to minimize the
total transportation and fuel costs. This was provided by applying the Large
Rank Value (LRV) procedure to convert hyena positions to travel sequences. This
also proposed a Flip and Swap rule in each iteration to improve the algorithm's
performance. Furthermore, a mathematical model was developed for the Fuel Consumption
Capacitated Vehicle Routing Problem (FCCVRP) by considering the load and FC
(fuel consumption) rates between the nodes. This indicated that several
population variations, iterations, and several nodes were used to investigate
the effectiveness of the HSHO algorithm. The results showed increased
population parameters, and HSHO iterations reduced the FCCVRP total
transportation costs. Furthermore, decreasing the fuel consumption rate between
nodes affected reduced fuel consumption. In addition, the proposed HSHO
produced a more optimal total transportation cost than the state-of-the-art
algorithm.
Capacitated vehicle routing problem; Distribution; Fuel consumption; Spotted hyena optimizer
The supply chain reportedly plays a vital role in organizational performance (Abdulameer, Yaacob, and Ibrahim, 2020; Ibrahim et al. 2020), through some activities such as procurement (Deepradit et al., 2020), production scheduling (Utama et al., 2019), and transportation (Sitompul and Horas, 2021; Benyamin, Farhad, and Saeid, 2021), where fuel consumption is found to be a crucial factor (Ozener and Ozkan, 2020; Norouzi, Sadegh-Amalnick, and Tavakkoli-Moghaddam, 2017). According to Sahin et al. (2009), a road transportation company in Shanghai, China, was responsible for 67.41% of fuel consumption within the total cost. This indicated that distribution route planning was a crucial factor to be considered in transportation activities (Utama et al., 2020a), due to significantly affecting efficiency (Utama et al., 2020c) and environmental protection (Dewi and Utama, 2021). Subsequently, most theories state that environmental problems are influenced by fuel consumption (Utama et al., 2021b), indicating that the transportation sector should contribute to the reduction of energy utilization. In popular routing activities, the issue of reducing fuel consumption is known as the FCCVRP (Fuel Consumption Capacitated Vehicle Routing Problem) (Utama et al., 2021a).
This was initially
introduced by Kuo (2010), which proposed the Simulated
Annealing (SA) procedure until several studies began to provide metaheuristic
and heuristic algorithms as solution sources. The techniques utilized in these
studies included Particle Swarm (PSO) (Poonthalir and Nadarajan, 2018) and Ant Colony Optimizations (ACO) (Yao et al.,
2015), Genetic Algorithm (GA) (Xiong, 2010), Simulated
Annealing (SA) (Normasari et al., 2019), Tabu Search (TS) (Suzuki, 2011), and the heuristic method Gaur, Mudgal,
and Singh
(2013). This indicated that the
distance to estimate fuel consumption was generally considered, although it was
still affected by the vehicle load between the nodes. In calculating fuel
consumption, loads have recently been considered in several FCCVRP studies,
indicating the development of metaheuristic algorithms such as SA (Xiao et
al., 2012), as well as Novel Hybrid TS (Niu et al.,
2018) and Hybrid PSO (Ali and
Farida, 2021). These aligned with Zhang, Wei, and Lim (2015), where a local evolutionary
search was provided for the problem. However, some previous FCCVRP studies
assumed that the Fuel Consumption Rate (FCR) between nodes was similar,
indicating that load and FCR subsequently affected FC (fuel consumption). This
motivated several study experts to investigate the issues of the FCCVRP by
developing a model emphasizing load-based inter-node FCR. These indicate that
full load is considered by the FCR level between nodes during loading and
no-load occurrences.
Therefore, this study
aims to develop a Hybrid Spotted Hyena Optimizer (HSHO) to solve FCCVRP
problems. This is because several studies did not use the algorithm to optimize
Fuel Consumption Capacitated Vehicle Routing Problems. According to Dhiman and Kumar (2017), the inspiration obtained from
the hunting behavior of hyenas led to the development of the SHO algorithm,
which was applied in various fields (Ghafori and
Gharehchopogh, 2021), such as allocation distribution (Naderipour et al., 2021), scheduling (Sahman, 2021), and transportation salesperson
problems (Nguyen et
al., 2020). This indicated that the
algorithm was developed by integrating the neighborhood search procedure to
solve FCCVRP. Therefore, the following contribution is observed (1) It proposes
a new FCCVRP model balancing the payload and FCR between nodes, (2) It presents
the influential analysis of the FCR on fuel consumption, and (3) It suggests a Novel
HSHO developed from the integration of the SHO and neighborhood search
procedures, respectively. The following sections are also observed, (a) Section
2 presents assumptions and problem definition, proposed algorithm, data
collection, and experiment setup, (b) Section 3 explains the results and
discussion, and (c) Section 4 shows the conclusions and recommendations for
further studies.
The FCCVRP
mathematical model was also developed from the method proposed by Xiao et al. (2012). It was
developed by considering the node-dependent FCR. The objective function of the
proposed model is formulated in Equation (1). Constraints of the proposed
mathematical model are presented in Equations (2)-(7), with the model being
developed as follows:
Based on Equation (1), the reduction of the Total Cost (TC) was the objective function to be achieved in this study. This indicated that the fixed budgets (travel and fuel costs) were involved at the TC. Subsequently, the proposed fuel cost considered the nodal FCR, distance, price, and transported load quantity. The constraints of the FCCVRP mathematical model used were as follows: (i) Constraint (2) ensured that each customer was only visited by one vehicle, (ii) Constraint (3) indicated that vehicles should come and go from each customer, (iii) Constraint (4) showed that a load of all vehicles was equal to the demand from all customers, (iv) Constraint (5) stated that the loads did not exceed the maximum vehicle capacity, (v) Constraint (6) ensured that customer demand should not be negative, and (vi) Constraint (7) was the decision variable's binary number [0.1].
2.2. Hybrid Spotted Hyena
Optimization (HSHO) Algorithm
According to the hunting phase, the best and optimal spotted hyenas had
good knowledge (fitness) of prey locations. This showed that the herd created a
cluster towards the best hyena, indicating the subsequent updates of their
positions. These behaviors were modeled in Equations (14) to (16), where
In the attacking prey (exploitation) phase, the observations were
modeled in Equation (18), where was determined as the new position of the
spotted hyena. This indicated a decrease in the value of
, changed with each additional iteration. It
also showed that the herd moved away and closer to locate and attack the prey.
When the value of |E|<1, E was subsequently generated from a variational
random number [-1, 1]. In the searching phase (exploration), the spotted hyenas
predictably moved away from the prey when the value of |E|>1.
According to the neighborhood search phase, an
exchange was applied to improve the algorithm performance in each iteration (Utama et
al., 2020b). This indicated that two neighborhood exchange rules
were proposed in this study, namely flip and swap, where a reversal was
observed by transforming and exchanging two randomly selected position vectors
of the spotted hyenas, as shown in Figures 2 and 3, respectively. The
repetition of the neighborhood search was also suggested as 0.25 x the number
of customers in each iteration. The LRV process was also applied as regards the
conversion to a sequence of trips on each iteration. This was then compared
with the previous processes to determine the best solution in the present
iteration. In addition, algorithm 1 presented the complete Pseudo-code of the
HHSO model, whose flow chart is shown in Figure 4.
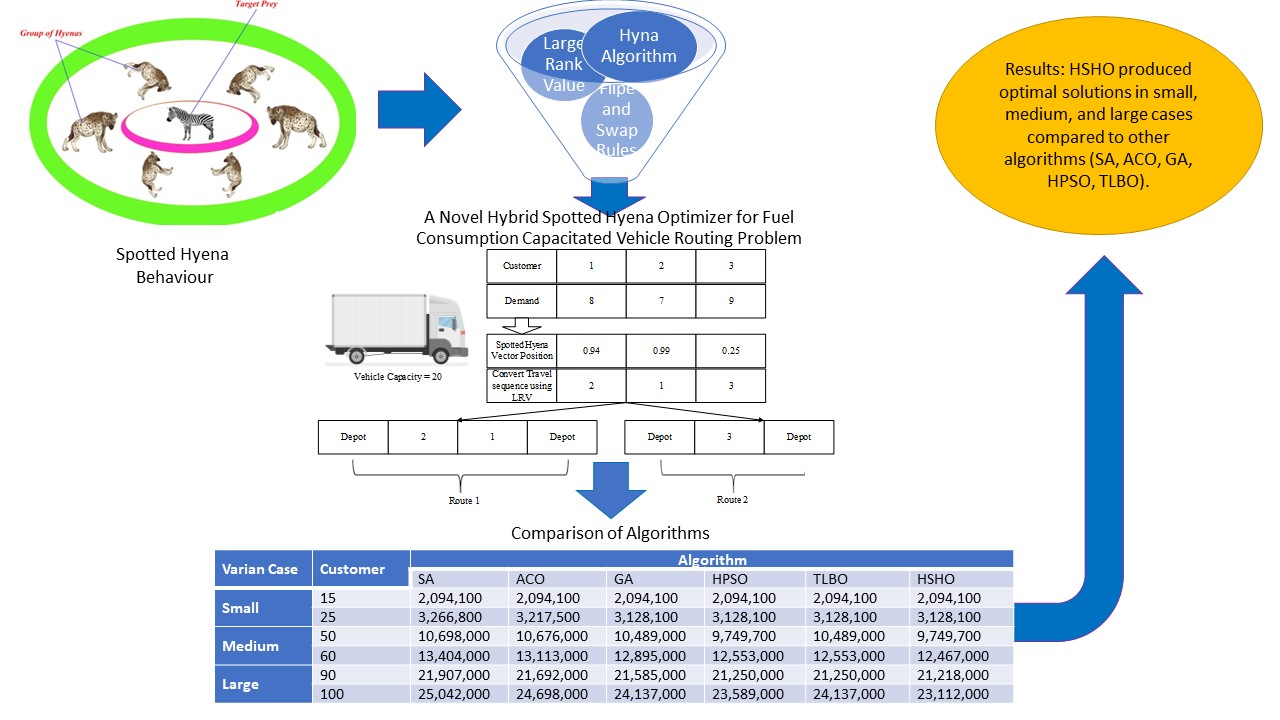
Figure 1 The conversion of the spotted hyena's possition to the travel route
2.3. Data collection and experiment setup
The data were obtained from the
case study of a mineral water distribution company in Mojokerto, Indonesia,
where the needs of 25 customers were to be met. The demand for each customer
(Di) was between 379 and 905 kg, with the vehicle capacity (Gm) estimated to
carry 2500 kg for one transport. The price of fuel per liter was also IDR 9,400,
with the fixed cost for delivery
being IDR 300,000.
Furthermore, the company had 1 Distribution Centre (DC) for customer needs, as
the distance observed between 1 DC and 25 consumers
was within 0.5-52
km. The FCRs from node i to j were also observed between 0.313-0.714 L/km and
0.625-1.429 L/km when the vehicle was unloaded
and fully loaded
respectively. Based
on the analysis, the iteration and population of HSHO were utilized with five
variations each to test the parameters of this algorithm on the total cost of
transportation. These five spotted hyena population parameters and HSHO
iteration were applied between 50-500 and 10-200, respectively. In this test,
approximately 25 trials were successfully conducted, with the best solution
being stored for use in the sensitivity analyses. This test was subsequently
used to examine the effect of the FCCVRP changes on the total, fixed, and fuel
costs, respectively.
According to the sensitivity
test, the transformed variables were This indicated that
the five variations of
were shifted from the initial values at each
node. In cases 1/2 and 4/5, the initial
value was decreased and increased by 0.1/0.05
and 1/1.5, respectively, with condition 3 completely utilizing this value. The
initial
values were also
decreased and increased by 0.1/0.05 and 1/1.5 in cases 6/7 and 9/10,
respectively, with condition 8 fully using this value. In
five data
variations were applied with a value range of 8500 to 10500. Furthermore, five
data variations were used for
between 150000-400000, as comparisons with the
state-of-the-art algorithms were applied to test the performance of HSHO. Based
on the case study data, random parameters were generated for
This indicated the
utilization of three variations, namely small (15 and 25 customers), medium (50
and 60 customers), and large (90 and 100 customers) cases, respectively. The
utilized comparison algorithm was also SA (Kuo 2010), ACO (Yao et al.,
2015), GA (Xiong, 2010), HPSO (Ali and
Farida, 2021), Teaching–Learning-Based Optimization
(TLBO) (Trachanatzi et al., 2021). These algorithms were then operated with 200 iterations and 500
population through the Matlab 2014a software on Windows 10 AMD A12 x64-64 8GB
RAM processor.
3.1. Effect of HSHO parameters on total transportation cost
The results of the HSHO effects
on the total cost of transportation are presented in Table 1, where increasing
iterations and population of the algorithm reduced the TC. However, decreased
iterations and populations led to high total transportation costs. This
indicated that large population parameters and HSHO interactions were needed to
solve the FCCVRP. For a population of 500 and 200 iterations, the optimal
result of TC was generated, as six routes were produced with a total
transportation cost of 3,128,100 IDR.
Table 1 The effects of HSHO on total transportation cost (IDR)
3.2. Sensitivity Analysis
The effects of the value changes towards the cost are shown in
Tables 2 and 3, respectively, where both parameters significantly affected the
total transportation budget. When the values of
were increased and decreased, the total and
fuel costs were also observed to be elevated and reduced, respectively. This
indicated that the changes and the increase/decrease of both values
significantly and insignificantly influenced the fuel and fixed costs,
respectively. Therefore, the distribution company needs to minimize the
values, to optimize the total transportation
cost.
Table 2 The effect of the value change towards the cost (IDR)
Table 3 The effect of the value change towards the cost
(IDR)
The effect of the value change towards cost is presented in
Table 4, where higher and lower
led to more expensive and cheaper fuel and
total transportation costs, respectively. This indicated that the
value had no significant effect on the fixed
cost.
Table 4 The effect of value change towards the cost (IDR)
The
results of the value change towards the cost is shown in
Table 5, where higher and lower
values led to more
expensive and cheaper transportation and fixed costs, respectively. This
indicated that fuel cost had no significant effect on
.
Table 5 The effect of value change towards the cost
(IDR)
3.3. Algorithm Comparison
Based on this study, a comparison of the HSHO algorithm was carried out
against the SA, ACO, GA, HPSO, and TLBO algorithms. The comparative results
towards the total transportation costs are shown in Table 6, where the proposed
HSHO algorithm produced more optimal TC than the HPSO, TLBO GA, ACO, and SA
algorithms. This was subsequently confirmed from the three variants of the
trial case (small, medium, and large), which produced a better and optimal
total transportation cost.
Table 6 Comparison of Algorithms to Total Transportation Costs (IDR)
This study presented the FCCVRP that considered the
load-based inter-node FCR. In this condition, a new mathematical model and
algorithm (FCCVRP and HSHO) were proposed as solution sources. Moreover, the
HSHO was a combination of the SHO algorithm with the neighborhood search
procedure. Based on the numerical experiments in the model, the changes
observed in affected the total transportation costs. This
indicated that the increase in population parameters and HSHO iterations
optimized the total transportation costs in the FCCVRP. The comparative
analysis of algorithms also showed that HSHO produced optimal solutions in
small, medium, and large cases compared to other algorithms. However, the
proposed algorithm had limitations in considering a single distribution center,
commodity delivery, and a homogeneous vehicle. Effective computation time was
also ignored in solving the FCCVRP, indicating that future studies should
consider multi-distribution centers, multi-commodity products, and vehicle
heterogeneity. In addition, computation time should be considered in
problem-solving.
Abdulameer, S.S.,
Yaacob, N.A., Ibrahim, Y.M., 2020. Measuring Leagile Supply
Chain, Information Sharing, and Supply Chain Performance: Pre-Test and Pilot
Test. International Journal of Technology, Volume 11(4), pp.
677–687
Ali, M.,
Farida,
B.N.I., 2021. Completion of FCVRP using Hybrid Particle Swarm Optimization
Algorithm. Jurnal Teknik Industri, Volume 22(1), pp.
98–112
Benyamin, A., Farhad,
S.G., Saeid, B., 2021. Discrete Farmland Fertility
Optimization Algorithm With Metropolis Acceptance Criterion For Traveling
Salesman Problems. International Journal of Intelligent Systems, Volume
36(3),
pp. 1270–1303
Deepradit, S.,
Ongkunaruk, P., Pisuchpen, R., 2020. Tactical Procurement
Planning under Uncertainty in Aromatic Coconut Manufacturing. International Journal of Technology, Volume 11(4), pp.
698–709
Dewi, S.K.,
Utama,
D.M., 2021. A New Hybrid Whale Optimization Algorithm for Green Vehicle Routing
Problem. Systems Science and Control Engineering, Volume
9(1),
pp. 61–72.
Dhiman, G., Kumar, V., 2017.
Spotted Hyena Optimizer: A Novel Bio-Inspired Based Metaheuristic Technique for Engineering
Applications. Advances in Engineering Software, Volume 114, pp.
48–70
Gaur, D.R., Mudgal, A.,
Singh,
R.R., 2013. Routing Vehicles to Minimize Fuel
Consumption. Operations Research Letters, Volume
41(6),
pp. 576–580
Ghafori, S.,
Gharehchopogh,
F.S., 2021. Advances in Spotted Hyena Optimizer: A Comprehensive Survey. Archives of Computational Methods in Engineering, Volume
2021,
pp. 1–22
Ibrahim, M.F., Putri,
M.M. Utama, D.M., 2020. A Literature Review On Reducing Carbon
Emission From Supply Chain System: Drivers, Barriers, Performance Indicators, znd Practices. In: 3rd
International Conference on Engineering Technology for Sustainable Development
(ICET4SD) 23–24 October 2019, 2020 Yogyakarta, Indonesia, p.
012034
Kuo, Y., 2010. Using Simulated
Annealing To Minimize Fuel Consumption For The Time-165dependent Vehicle
Routing Problem. Computers and Industrial Engineering, Volume
59(1),
pp. 157–165
Naderipour, A.,
Abdul-Malek, Z., Hajivand, M., Seifabad, Z.M., Farsi, M.A., Nowdeh, S.A.,
Davoudkhani,
I.F., 2021. Spotted Hyena Optimizer Algorithm for Capacitor
Allocation in Radial Distribution System With Distributed
Generation and Microgrid Operation Considering Different
Load Types. Scientific Reports, Volume
11(1),
pp. 1–15
Nguyen, V.D., Nguyen,
T., Nguyen, T.L., Tran, V.C., Truong, H.B.,
2020. Spotted Hyena Optimizer: An Approach to Travelling Salesman Problems. In: 12th
International Conference, ICCCI, 2020 Da Nang, Vietnam, pp.
217–228
Niu, Y., Yang, Z.,
Chen, P., Xiao, J., 2018. A Hybrid Tabu Search Algorithm
for a Real-World Open Vehicle Routing Problem Involving Fuel Consumption
Constraints. Complexity, pp. 1–12
Normasari, N.M.E., Yu,
V.F., Bachtiyar, C., Sukoyo, 2019. A Simulated Annealing Heuristic
for the Capacitated Green Vehicle Routing Problem. Mathematical Problems in
Engineering, Volume 2019, p. 2358258
Norouzi, N.,
Sadegh-Amalnick, M., Tavakkoli-Moghaddam, R., 2017. Modified Particle
Swarm Optimization In A Time-Dependent Vehicle Routing Problem: Minimizing Fuel
Consumption. Optimization Letters, Volume
11(1),
pp. 121–134
Ozener, O., Ozkan,
M., 2020. Fuel Consumption And Emission Evaluation of a Rapid Bus Transport
System At Different Operating Conditions. Fuel, Volume
265,
p, 117016
Poonthalir, G.,
Nadarajan,
R., 2018. A Fuel Efficient Green Vehicle Routing Problem with Varying Speed
Constraint (F-GVRP). Expert Systems with Applications, Volume
100,
pp. 131–144
Sahin, B., Yilmaz, H.,
Ust, Y., Guneri, A.F., Gulsun, B., 2009. An Approach
For Analysing Transportation Costs and a Case Study. European Journal of Operational Research, Volume 193(1), pp.
1–11
Sahman, M.A., 2021. A Discrete
Spotted Hyena Optimizer For Solving Distributed Job Shop Scheduling Problems. Applied Soft Computing, Volume 106, p.
107349
Sitompul, C.,
Horas,
O.M., 2021. A Vehicle Routing Problem with Time Windows Subject to the
Constraint of Vehicles and Good’s Dimensions. International Journal of
Technology, Volume 12(4), pp. 865–875
Suzuki, Y., 2011. A New
Truck-Routing Approach for Reducing Fuel
Consumption and Pollutants Emission. Transportation Research Part D: Transport and Environment, Volume
16(1),
pp. 73–77
Trachanatzi, D.,
Rigakis, M., Marinaki, M., Marinakis, Y., 2021. A
Teaching–Learning-Based Optimization Algorithm For The Environmental
Prize-Collecting Vehicle Routing Problem. Energy Systems, Volume
2021,
pp. 1–28
Utama, D.M., Dewi,
S.K., Wahid, A., Santoso, I., 2020a. The Vehicle Routing
Problem For Perishable Goods: A Systematic Review. Cogent Engineering, Volume
7(1),
p. 1816148
Utama, D.M., Farida,
B.N.I., Fitriani, U., Ibrahim, M.F., Widodo, D.S., 2021a.
Hybrid Henry Gas Solubility Optimization: An Effective Algorithm for Fuel
Consumption Vehicle Routing Problem. Jurnal Ilmiah Teknik Industri, Volume
20(2),
pp. 141–152
Utama, D. M., Fitria,
T.A., Garside, A.K., 2021b. Artificial Bee Colony
Algorithm for Solving Green Vehicle Routing Problems with Time Windows. In: Virtual Conference on
Engineering, Science and Technology (ViCEST) 2020, 2021/06/01 2021b
Kuala Lumpur, Malaysia, p. 012043
Utama, D.M., Widodo, D.S., 2021.
An Energy-Efficient Flow Shop Scheduling Using Hybrid Harris Hawks Optimization.
Bulletin of Electrical Engineering and Informatics, Volume
10(3),
pp. 1154–1163
Utama, D.M., Widodo,
D.S., Ibrahim, M.F., Dewi, S.K., 2020b. An Effective Hybrid Ant
Lion Algorithm To Minimize Mean Tardiness on Permutation Flow
Shop Scheduling Problem. International Journal of Advances in Intelligent
Informatics, Volume 6(1), pp. 23–35
Utama, D.M., Widodo,
D.S., Ibrahim, M.F., Dewi, S.K., 2020c. A New Hybrid Butterfly
Optimization Algorithm for Green Vehicle Routing Problem. Journal of Advanced Transportation, Volume 2020, p.
8834502
Utama, D.M., Widodo,
D.S., Wicaksono, W., Ardiansyah, L.R., 2019. A New Hybrid
Metaheuristics Algorithm For Minimizing Energy Consumption In The Flow Shop
Scheduling Problem. International Journal of Technology, Volume
10(2),
pp. 320–331
Xiao, Y., Zhao, Q.,
Kaku, I., Xu, Y., 2012. Development of a Fuel Consumption
Optimization Model For The Capacitated Vehicle Routing Problem. Computers and Operations Research, Volume 39(7), pp.
1419–1431
Xiong, H.,
2010. A Fuel Consumption Objective of VRP and the Genetic Algorithm. In: 2010 International
Conference on E-Product E-Service and E-Entertainment, pp. 1–4
Yao, E., Lang, Z.,
Yang, Y., Zhang, Y., 2015. Vehicle Routing Problem
Solution Considering Minimising Fuel Consumption. IET Intelligent Transport
Systems, Volume 9(5), pp. 523–529
Zhang, Z., Wei, L.,
Lim,
A., 2015. An Evolutionary Local Search For The Capacitated Vehicle Routing
Problem Minimizing Fuel Consumption Under Three-Dimensional Loading Constraints.
Transportation Research Part B: Methodological, Volume
82, pp.
20–35
