A Two-dimensional Maintenance Service Contract Considering Availability and Maintenance Cost

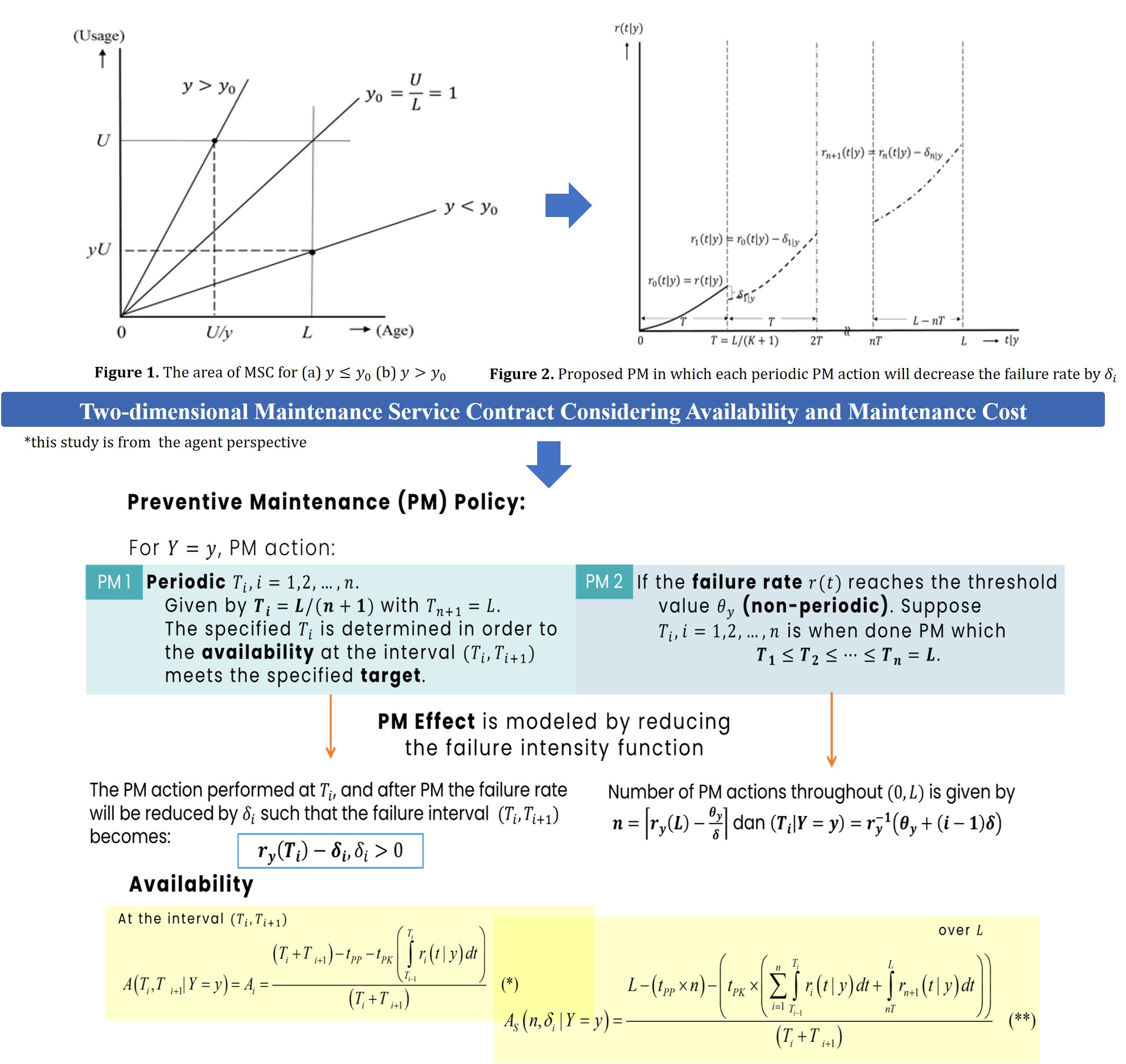
In this paper, we study a two- dimensional Maintenance Service Contract (MSC) characterized by two limits (dimensions) of age and usage. It is considered that an agent offers a two-dimensional MSC by guaranteeing a certain level of equipment available to consumers. The agent needs to reduce the total maintenance cost to offer competitive MSC prices. Preventive maintenance actions (PM) are periodically carried out, and each PM action is considered to improve reliability modeled by reducing the failure rate function. Two decision variables (the PM interval (T) and the reduction in the intensity function  are obtained by considering two performance measures that are relevant to agents and consumers (i.e., availability and total maintenance cost). A numerical example is presented by considering three types of equipment usage rates: low, medium, and high. The optimization of the two performance measures can ensure availability targets and, at the same time, minimize total maintenance costs.

Availability; Imperfect preventive maintenance; Maintenance service contract Total cost; Two-dimensional

Maintenance Service Contract (MSC) is defined as an equipment maintenance contract that agents offer to consumers within a certain period. Maintenance contracts, generally, are characterized by a time limit (e.g., 1 year), called an MSC with one dimension. However, for equipment such as dump trucks whose failure patterns are affected by age and use, it is necessary to include a usage limit (e.g., 100,000 km) in addition to the age limit. Different types of equipment may have different ways of measuring usage. For example, a photocopier's usage can be measured by the number of copies made, while a machine tool's usage can be measured by the hours it is used. This MSC is referred to as an MSC with two dimensions. To appeal to consumers, the MSC may include promised equipment performance (e.g., Target 94% equipment availability) in addition to the price charged. A comprehensive review of MSC can be found in Murthy and Jack (2014), and MSC is studied  from the perspectives of consumers (MSC recipients) and agents (MSC providers).

       From the consumer side, equipment used to support business processes will deteriorate with age and use, and eventually, failure will occur (Jiang and Murthy, 2008). Maintenance is an effective way to slow down the deterioration of equipment so that failure can be minimized and availability can be kept high (Pariaman et al., 2017; Suthep and Kullawong, 2015; Jackson and Pascual, 2008). Consumers who own equipment, generally need MSC because maintenance activities are not their main business (core business), so they do not need to be done in-house. 

Using an agent to maintain equipment through a Maintenance Service Contract (MSC) is more cost-effective and reliable than in-house maintenance, which requires expensive investments in human resources, equipment and technology. MSC offers consumers the benefits of saving on maintenance costs and improving equipment performance. Many studies have explored MSC from the consumer's perspective, including research conducted by Huber and Spinler (2012) and Jensen and Stonecash (2009). In general, research from the consumer’s point of view always wants (i) minimum cost or maximum profit, with additional considerations of other performance measures such as (ii) service quality (eg. delivery time) (De-Almeida, 2007) (iii) product reliability (Laksana and Hartman, 2010), or (iv) availability (Datta and Roy, 2010). Due to the important role of maintenance in maintaining the condition of equipment, the agents respond proactively to the consumers’ needs by offering MSCs that promise high availability. In addition to getting regular income, agents can also build good relationships with consumers, which positively impacts the agent’s image (brand building).

From the agent’s point of view, research was carried out by Tarakci et al. (2006), where the agent offers specific incentives based on the combination of target uptime and bonuses in the contract to attract consumers. In addition, reliability improvement is also considered. Generally, the agent looks for the optimal PM time interval to fulfill the performance promise to the customer, which maximizes the profit. MSC can be grouped into two categories: one-dimension MSC and two-dimension MSC. One-dimensional MSC is characterized by a one-time limit (age). For example, the MSC of a piece of equipment is for one year, while the two-dimension MSC is characterized by an area of a two-dimensional plane where one dimension describes a time limit and the other a usage limit (Iskandar et al., 2014). One-dimensional MSC research has considered several important performance measures for agents (i.e., total cost and benefit) as well as consumers (i.e., reliability and availability). First, many MSC studies consider profit performance measures (Darghouth, Ait-kadi, and Chelbi, 2017; Hamidi, Liao, and Szidarovszky, 2013; Chang and Lin, 2012). Second, the reliability performance measure is considered in addition to the benefits (Laksana and Hartman, 2010). Third, the availability performance measure is also involved (Su and Cheng, 2018; Iskandar et al., 2014). The effect of PM's actions on increasing reliability can be represented through a reduction in (i) failure rate or (ii) virtual age. Some of them are researched by Darghouth, Ait-kadi, and Chelbi (2017) and Pasaribu, Husniah, and Iskandar (2012), who specifically examined one-dimensional MSC with periodic PM policies and the impact of PM reducing a virtual age. Other works are the research of Husniah et al. (2019) and Yeh and Chang (2007), which examine one-dimensional MSC with a periodic PM policy model using an intensity reduction function. There is also research by Iskandar and Husniah (2017) and Yeh, Kao, and Chang (2009), who investigate one-dimensional contracts using a PM policy that ensures equipment reliability.

Meanwhile, two-dimensional MSC studies have not received much attention. As in one-dimensional MSC, the most commonly used performance measure in two-dimensional MSC is profit (Huang, Gau, and Ho, 2015; Husniah et al., 2014). No studies have considered the availability of two-dimensional MSCs. At the same time, consumers want high equipment availability to be guaranteed. The motivation to prioritize availability is because the losses (costs) due to equipment downtime are very large. For example, the breakdown of equipment such as draglines (in the mining business) and airplanes (in the transportation business) will result in huge losses for the company operating the equipment. Performance in two-dimensional MSC can be achieved by implementing various preventive maintenance (PM) policies, which can be divided into two categories, namely periodic and non-periodic (Jiang and Murthy, 2008).

In this paper, we propose a two-dimensional MSC that implements the imperfect PM policy carried out periodically. The effect of the PM action on the two-dimensional MSC will be developed by extending the formulation of the one-dimensional MSC. As in the one-dimensional MSC studied by Yeh and Chang (2007), It is assumed that the effect of PM reduces the intensity function. Furthermore, this paper focuses on two-dimensional MSC, The study is carried out from the agent's point of view, considering two performance measures, namely: (i) equipment availability and (ii) total maintenance costs, and involving two decision variables, i.e., the PM time interval (T), and the failure rate reduction value  for each PM. As a result, the main contributions of this paper are (i) developing a PM policy that ensures the equipment availability target with minimum costs and (ii) obtaining optimal solutions of PM policies for a two-dimensional MSC with two objective functions, namely maximizing availability and minimizing total cost. This is in accordance with the goals desired by consumers for MSC, which are to ensure high availability (for example, 94%) and simultaneously meet the agency's goal of minimizing total maintenance costs. This paper is organized as follows: The model formulation is given in Section 2, which includes a discussion of the two-dimensional MSC formulation, failure modeling, and PM impact modeling. Section 3 describes an optimization to find the optimal solution that guarantees target availability with the minimum total cost. Section 4 provides numerical examples and a discussion of the results. Finally, we present conclusions and further research topics in Section 5.

Model Formulation

This section will detail the two-dimensional MSC under study, failure modeling, and PM effect modeling.

2.1. Two-dimensional MSC

      Consider a two-dimensional MSC for equipment (e.g. dump trucks), which is characterized by two parameters, L (time limit) and U (usage limit). For example, a maintenance contract for a dump truck with a time limit of 1 year and a usage limit of 100,000 km. Thus, these two contract limits form a rectangular area (Iskandar et al., 2014). Suppose that the equipment with the rate of use  is said to be moderate (normal) usage rate,  low usage rate, and high usage rate . The contract will end at for a low usage and at for high use. The boundary region of the two-dimensional MSC is given by  and   (see Figure 1).

Figure 1 The area of MSC for (a)  and (b) 

Figure 2 Proposed PM in which each periodic PM action will decrease the failure rate by  

2.2.  Failure Modeling

Equipment failures that occur randomly during the contract period are considered random points that fall in the maintenance contract area (which is rectangular). There are three approaches to modeling random points (equipment failure) on a two-dimensional plane (Murthy and Jack, 2014). In this paper, we shall use the formulation of a one-dimensional point process as has been done by Iskandar, Murthy, and Jack (2005). Let  the random variable represents the usage rate of the equipment (e.g., distance traveled per unit of time (300km/day), machine hours per day). Conditional on ,  then random points will occur along the time axis (t) so that it can be modeled with a one-dimensional point process. It is assumed that each consumer has a constant use rate and can be different for different consumers.
     Equipment is repairable, and the equipment failure over time is modeled with an intensity function (Iskandar and Murthy, 2003). Suppose  is the conditional failure rate function on . It is assumed that all failures are fixed with minimal repair. Hence, the failure occurrence will follow the Non-Homogeneous Poisson Process (NHPP) with the intensity function  where   is a non-decreasing function of t and y. Iskandar and Murthy (2003) provide a formulation of the intensity function as a first-order polynomial function. Another formulation that can be used is the Accelerated Failure Time (AFT) (Iskandar et al., 2014), and this formulation will be used in this paper.  

     Suppose is a random variable representing the time of the first failure for a given usage. The distribution function  is given by the Weibull distribution function. Next, the effect of usage patterns on equipment failure modeling will be explained. It is considered that equipment with a high usage rate  will deteriorate faster than equipment with a low usage rate . The AFT formulation can be used to model the effect of this usage pattern as follows. Let  be the time to first failure for usage rate  The relationship of and is given by,  If the distribution function for  is given by , with   is the scale parameter, then the distribution function for is the same as the distribution function for but with the scale parameter given by: Thus, we get . The intensity and cumulative functions with respect to are given by  and is a density function with respect to 

2.3. PM Policy

   The agent requires a proper PM policy to reduce failures and downtime, and this will increase availability. In this paper, two PM policies are considered.

2.3.1. PM Policy 1

   PM actions are carried out periodically or at the time of . Given by  , where L is the contract term. In this policy, the specified value of  is determined to ensure the availability at the interval meets the defined target and will be described in Section 2.5. 

     PM is done if the failure rate reaches the threshold value . Suppose   is when done PM is  This policy was proposed by Yeh and Chang (2007) to reduce the level of failure rate. So,  was determined to minimize the expected number of failures during L. 

2.4.  PM Effect Modelling

2.4.1. PM Policy 1

     As mentioned previously, the effect of PM action can be modeled through (a) virtual age or (b) failure intensity function. Here, the impact of PM is modeled by reducing the failure intensity function and is described as follows. For the use of , the PM action performed at  and after PM, the failure rate will be reduced bysuch that the failure rate in the interval becomes  becomes (See Fig. 2). The decision variable depends on y. One can group consumers by usage rate y – e.g., low usage rate moderate usage rate and high usage rate; hence each usage group has a unique .

2.4.2. PM Policy 2

    In this PM policy, whenever PM (if the failure rate reaches ), failure rate will be reduced by . For a given Y = y, number of PM actions throughout the period L is given by  Note: This approach extends Yeh and Chang (2007) to a two-dimensional case.  

2.5. Availability and Total Maintenance Cost

2.5.1. Availability

    The contract period is divided into intervals with the length of the first and last intervals Suppose that shows the availability value at the interval for is given by: 

where are the length of time PM and CM action. The formula (availability in interval )is used to get the optimal value that is at least the same as the availability target. Availability during the contract L or the entire interval is described as follows. Suppose   is the expected availability over  conditional on Y = y and it is given by:

     In practice, equipment owners want high availability of equipment to achieve their production targets . In this, we propose an approach to guarantee an availability target of in the entire MSC period by determining the failure rate reduction, such that the availability of each interval is at least equal to the availability target. 

2.5.2. Total Maintenance Cost

    PM Policy 1:        Total maintenance costs include minimal repair costs (including expected downtime penalties) and PM action costs. The total expected cost of a two-dimensional MSC over the period is given by: 

   PM Policy 2:   The formula for total maintenance costs consists of minimal repair costs (including expected penalties due to downtime) and PM action costs. The expected total cost for the period is given by

Optimal Decision

    This section discusses the optimization scheme (Optimization Schema) of the two-dimensional MSCs under consideration.

3.1. Two-dimensional MSC with PM 1 Policy (Proposed)

Optimization Scheme 1: Find the value which maximizes  (given in (2)), and then calculate the total maintenance cost given in (3). Note: Here, the maximization  is done without any constraint on the availability value.

Optimization Scheme 2: Find the value of  which maximizes  (given in (2)) with the availability constraint i.e., , and then calculate the total maintenance cost by (3).

Optimization Scheme 3: Find the value of  by considering availability and total cost together. This is done using optimization with two objective functions. Using the Weighted Sum method from the study of Grodzevich and Romanko (2006), the structure of the optimization function with two objectives is given below.

Hence, the value of   obtained will maximize the availability and minimize the total cost simultaneously (not done sequentially as in the previous two schemes).

3.2. Two-dimensional MSC with PM Policy 2

Again, the three optimization schemes are also used to find the optimal solution.

Optimization Scheme 1: (i) First, using the algorithm proposed by Yeh and Chang (2007) finding the optimal value of which minimizes the expected total cost. (ii) Second, based on the optimal value of (i), then calculate the availability with the equation in (2).

Optimization Scheme 2: In this scheme the value of  must first meet the availability target  and then calculate the total cost with the value of  obtained. Thus, Steps 4 and 5 in the algorithm of Yeh and Chang (2007)  need to be modified to :

Optimization Scheme 3: Find the value   by considering availability and total cost together. The structure of the optimization function with two objectives is given below.

Step 1. Set 

Step 2. Solve the system of equations with the objective function:

    Consider that  is Weibull distribution with , where is the scale parameter and is the shape parameter. Suppose that each failure incurs costs (including the minimal repair cost and possible penalty cost) and the cost for performing a PM action with maintenance degree . A similar form of maintenance cost is used by Supriatna et al. (2020). These parameter values were used in Yeh and Chang (2007) and will be considered in this section given in Table 1.

In this section, we shall evaluate the performance of two-dimensional MSC with PM Policy 1 (proposed PM) and two-dimensional with PM Policy 2.

4.1. Discussion of MSC 2D results with PM 1

   Tables 2 and 3 show the results for low usage (y=0.9), comparing results with Schemes 1 and 2 and then results with Schemes 2 and 3.  From Tables 2 and 3, we have the following findings. Increasing the parameter value of gives the same or increased availability for Schemes 1-3. This is expected because larger means higher reliability (this agrees with the result of Yeh and Chang (2007) for a 1D MSC case). The results with Scheme 2 always give higher availability values than Scheme 1. In addition, Scheme 2 also provides a lower total cost of up to 71.70% (see Table 2, for the parameter ) than the results of Scheme 1. The total cost is smaller because the PM Policy 1 improves reliability by optimizing  (is not constant). Furthermore, Scheme 3 also provides an availability value that is as large as the results of Scheme 2. The advantage of Scheme 3 is that the total cost obtained is lower than the total cost with Schemes 1 and 2. Total maintenance costs can be reduced by up to 71.70% (see Table 2 on parameters ). Thus, the best optimization scheme for PM 1 policy is Scheme 3, and this pattern also holds for medium and high usage rates (Note: the results cannot be included due to the number of page limitations of a paper).

Table 3 Results of MSC 2D with PM 1 using Schemes 2 and 3 for low usage (y=0.9)

4.2. Discussion of MSC 2D results with PM 2

     We have the following findings from Table 4. The results of Schemes 1 and 2 are not different. Scheme 3, which optimizes two performance measures simultaneously, gives the best results. Availability using Scheme 3 increases up to 0.10%. In addition, the total cost of maintenance can also be reduced by up to 43.81% (see Table 4, in parameter . The Scheme 3 is also the best for availability and total cost measures for medium and high usages.

4.3. Comparison between the two MSC 2D

     In each of the 2D MSCs considered, Scheme 3 gives the best results. MSC 2D with PM 1 is superior both in terms of performance measures of availability and total cost (see Table 5). Regarding availability, MSC 2D with PM 1 is up to 0.40% superior (see Table 5, in parameter ) to MSC 2D with PM Policy 2. Meanwhile, regarding total costs, MSC 2D with PM 1 provides a smaller total cost of almost 1/4 times the 2D MSC with PM 2 - see Table 8 with the 2D MSC parameter  with PM 2 up to 396.38%.

     The advantage of the PM 1 policy is the optimization of (the reduction in intensity function) for each PM action. Whereas in the PM 2 policy, the value for each PM action is the same, even though the longer the age of the equipment or the higher the usage rate. This advantage makes PM Policy 1 (proposed PM) superior to PM Policy 2. For an agent who offers a 2D MSC with an availability target, the results of this study are helpful in determining maintenance policies that can meet availability targets with minimum total maintenance cost.

 

In this paper, a two-dimensional Maintenance Service Contract (MSC) study is conducted with (1) periodic and (2) non-periodic PM policies by considering availability performance measures and total maintenance costs. The two-dimensional MSC with periodic PM policy provides the best performance – in terms of availability (can guarantee an availability target) and low total costs at any rate of usage considered.  Here, a two-dimensional MSC study was conducted from the agent's point of view. One of the further research topics is a two-dimensional MSC study that takes into account the two parties- i.e., the agent and the consumer, who are very concerned about the price of MSC. This topic can be modeled by a game theory formulation and provides optimal results for both parties. In addition, from an equipment maintenance perspective, MSC can also consider condition-based preventive maintenance options so equipment performance can be even better. Furthermore, as the maintenance services can be provided by the Original Equipment Manufacturer (OEM) or the agent, another interesting topic is to study a 2D MSC involving three parties– i.e., the Original Equipment Manufacturer (OEM), the agent, and the consumer. The integration of three-party decision problems is an interesting topic because it can mathematically describe the relationship of competition or cooperation between agents. The formulation can be done using two-level game theory and it is expected to choose the optimal option for consumers as well as the optimal three-party coordinated option. The findings will be very beneficial for the parties involved with the following details: (i) the agent can achieve the availability target with minimum total maintenance costs, and (ii) the consumer benefits from the optimal target of equipment availability and MSC price to maximize profit. Research on these topics is on the way.

    The research and study were supported by the Ministry of Research, Technology, and Higher Education (Kementrian Ristek-Dikti) Indonesia through the Program Magister menuju Doktor untuk Sarjana Unggul (PMDSU).

Chang, Wen Liang, and Lin, Jyh-Horng, 2012. Optimal maintenance policy and length of extended warranty within the life cycle of products. Computers and Mathematics with Applications, Volume 63, pp. 144–150

Darghouth, M.N., Ait-kadi, D., Chelbi, A., 2017. Joint optimization of design, warranty and price for products sold with maintenance service contracts. Reliability Engineering and System Safety, Volume 165, pp. 197–208

Datta, P.P., Roy, R., 2010. Cost modelling techniques for availability type service support contracts: a literature review and empirical study. CIRP Journal of Manufacturing Science and Technology, Volume 3, pp. 142–157

De-Almeida, A.T., 2007. Multicriteria decision model for outsourcing contracts selection based on utility function and ELECTRE method. Computers & Operations Research, Volume 34, pp. 3569–3574

Grodzevich, O., Romanko, O., 2006. Normalization and other topics in multi-objective optimization. In: Proceedings of the Fields-MITACS Industrial Problems Workshop, pp. 89–101

Hamidi, M.,  Liao, H., Szidarovszky, F., 2013. A game-theoretic model for establishing maintenance service contracts. In: IIE Annual Conference and Expo, pp. 3178–3187

Huang, Y.-S., Gau, W.-Y., Ho, J.-W., 2015. Cost analysis of two-dimensional warranty for products with periodic preventive maintenance. Reliability Engineering and System Safety, Volume 134, pp. 51–58

Huber, S., and Spinler, 2012. Pricing of full-service contracts. Eur J Oper Res, Volume 222, pp. 113–131

Husniah, H., Maulana, H.A., Pasaribu, U.S., and Iskandar, B.P., 2019. Two-dimensional lease contract with preventive maintenance using bivariate Weibull. International Journal of Industrial Engineering: Theory Applications and Practice, Volume 26(1), pp. 48–58

Husniah, H., Pasaribu, U.S., Cakravastia, A., Iskandar, B.P., 2014. Two dimensional maintenance contracts for a fleet of dump trucks used in mining industry. Applied Mechanics and Materials, Volume 660, pp. 1026–1031

Iskandar, B.P., Husniah, H., 2017. Optimal preventive maintenance for a two dimensional lease contract. Computers and Industrial Engineering, Volume 113, pp. 693–703

Iskandar, B.P., Murthy, D.N.P., 2003. Repair-replace strategies for two-dimensional warranty policies. Mathematical and Computer Modelling, Volume 38, pp. 1233–1241

Iskandar, B.P., Murthy, D.N.P., Jack, N., 2005. A new repair-replace strategy for items sold with a two-dimensional warranty. Computers and Operations Research, Volume 32(3), pp. 669–682

Iskandar, B.P., Pasaribu, U.S., Cakravastia, A., Husniah, H., 2014. Maintenance service contracts for a fleet of dump trucks used in mining industry. In: CIE 2014 - 44th International Conference on Computers and Industrial Engineering and IMSS 2014 - 9th International Symposium, pp. 2480–2491

Jackson, C., Pascual, R., 2008. Optimal maintenance service contract negotiation with aging equipment. European Journal of Operational Research, Volume 189, pp. 387–398

Jensen, P.H., Stonecash, R.E., 2009. Contract type and the cost of provision: evidence from maintenance service contract. Fiscal Studies, Volume 30, pp. 279–296

Jiang, R., Murthy D.N.P., 2008. Maintenance: decision models for management. Beijing, China: Science Press

Laksana, K., Hartman, J.C., 2010. Planning product design refreshes with service contract and competition considerations. International Journal of Production Economics, Volume 126(2), pp. 189–203

Murthy, D.N.P., Jack, P., 2014. Extended warranties, maintenance service and lease contracts: modeling and analysis for decision-making. London: Springer-Verlag

Pariaman, H., Garniwa, I., Surjandari, I., Sugiarto, B., 2017. Availability analysis of the integrated maintenance technique based on reliability, risk, and condition in power plants. International Journal of Technology, Volume 3, pp. 497–507

Pasaribu, U.S., Husniah, H., Iskandar, B.P., 2012. Stochastic system in discrete preventive maintenance and service contract. In: Proceedings of 2012 IEEE Conference on Control, Systems and Industrial Informatics, ICCSII 2012, pp. 250–254

Su, C., Cheng, L., 2018. Design of maintenance service contract upon the expiration of availability-based warranty. In: Proceedings of International Conference on Computers and Industrial Engineering, CIE, Volume 2018

Supriatna, A., Singgih, M.L., Widodo, E., and Kurniati, N., 2020. Overall equipment effectiveness evaluation of maintenance strategies for rented equipment. International Journal of Technology, Volume 11(3), pp. 619–630

Suthep, B., Kullawong, T., 2015. Combining reliability-centered maintenance with planning methodology and applications in hard chrome plating plants. International Journal of Technology, Volume 3, pp. 442–451

Tarakci, H., Tang, K., Moskowitz, H., Plante, R., 2006. Incentive maintenance contracts for channel coordination. IIE Transactions, Volume 38, pp. 671–684

Yeh, R.H., Chang, W.L., 2007. Optimal threshold value of failure-rate for leased products with preventive maintenance actions. Mathematical and Computer Modelling, Volume 46(5-6), pp. 730–737

Yeh, R.H., Kao, K.-C., Chang, W.L., 2009. Optimal preventive maintenance policy for leased equipment using failure rate reduction. Computers and Industrial Engineering, Volume 57(1), pp. 304–309