Near-Collapse Probability of RC Frames in Indonesia Under Repeated Earthquakes Containing Fling-Step Effect
Corresponding email: adefaisal@umsu.ac.id
Published at : 04 Apr 2023
Volume : IJtech
Vol 14, No 2 (2023)
DOI : https://doi.org/10.14716/ijtech.v14i2.4989
Faisal, A., Anshari, A., Nazri, F.M., Kassem, M.M., 2023. Near-Collapse Probability of RC Frames in Indonesia Under Repeated Earthquakes Containing Fling-Step Effect. International Journal of Technology. Volume 14(2), pp. 339-350
| Ade Faisal | Program Studi Teknik Sipil, Universitas Muhammadiyah Sumatera Utara, Jl. Mukhtar Basri No.3, Medan 20238, Indonesia |
| Afiful Anshari | Program Studi Teknik Sipil, Universitas Muhammadiyah Sumatera Utara, Jl. Mukhtar Basri No.3, Medan 20238, Indonesia |
| Fadzli Mohamed Nazri | School of Civil Engineering, Engineering Campus, Universiti Sains Malaysia, 14300, Nibong Tebal, Penang, Malaysia |
| Moustafa Moufid Kassem | School of Civil Engineering, Engineering Campus, Universiti Sains Malaysia, 14300, Nibong Tebal, Penang, Malaysia |
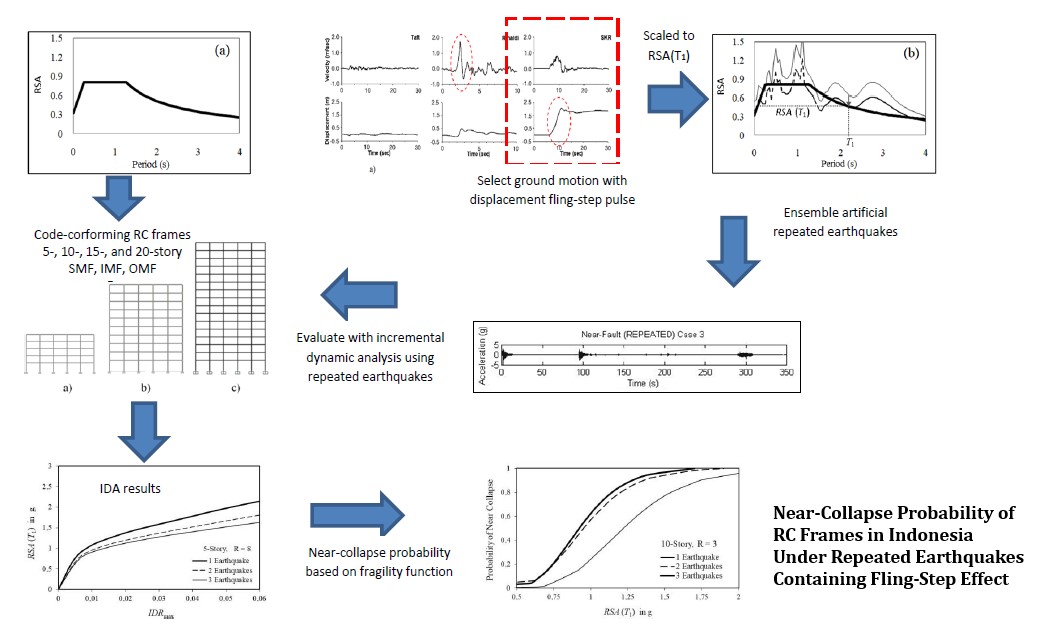
The velocity pulse and displacement
fling-step pulse signatures may be present in a near-field earthquake ground
motion record. It is generally known that near-field ground motion with pulse
effects accelerated the building drift. The damage of building can also occur
as a result of two or three earthquakes within the building's lifespan. The
repeated earthquakes could cause minor to severe damage to the building,
including structural collapse. This includes earthquakes with fling-step pulse,
which impact is underexamined in the existing studies. Therefore, the objective
of this study is to assess the impact of repeated earthquakes with displacement
of the fling-step pulse on the near-collapse probability of 5-, 10-, 15 and 20-story concrete frames.
Based on the response modification factor R = 8, 5, and 3, the frames are
classified as special, intermediate, and ordinary, respectively. The result
shows that the near-collapse probability of repeated earthquakes is more likely
to occur on the concrete frames which reaches intensity measure of 27.0% than
the effect of single earthquakes.
Incremental dynamic analysis; Interstory drift; Nonlinear response history analysis; Probability of near-collapse
Indonesia is flanked by tectonic plates and is repeatedly experiencing
devastating earthquakes due to plate movement. The collision of Eurasian and
Indo-Australian plates has produced devastating earthquakes of the West coast
of Sumatera, i.e. Mw > 9.0 in the Northern part (Prakoso
et al., 2017) and Mw > 8.0 in the Southern part (Mase, 2018). In the Lombok region of central
Indonesia, the collision of these plates has caused earthquakes with Mw >
7.0 (Pramono et al., 2018). These
types of earthquakes tend to occur repeatedly in the same tectonic region with
return periods of hundreds or tens of years, or even shorter. One of the
instances is the Mw 6.4 earthquakes that is followed by Mw 6.8 one which struck
the Lombok region on 07/29/18 and 08/05/2018, respectively (Pramono et al., 2018).
A study of
reinforced concrete (RC) frames subjected to high vibration found a clear link
between interstory drift and structural failure. When the interstory drift
reaches 3% in a 10-story RC building, the column sustains initial damage (Dymiotis et al., 1999).
The
fragility curves of 9 RC frames, which are designed according to the seismic
code, are investigated by Kalantari and Roohbakhsh
(2019). In this study, the near-collapse and collapse limit states due
to repeated earthquakes are evaluated as
well. Oggu and Gopikhrisna (2020)
investigates the probability of collapse of regular and irregular RC structures
affected by repeated earthquakes. It shows that the intensity measure for the
probability of collapse (IM) of the regular structure is 3.33% less than IM caused by a single earthquake. More recently, Di Sarno and Pugliese (2021) reports that the
effect of repeated earthquakes on the existing RC structures increases seismic
vulnerability to 17%. Nevertheless, a lower IM result is also found in the
study of the probability of collapse due to repeated earthquakes in an existing
4-story RC structure in comparison with the effect of a single earthquake (Aljawhari et al., 2021).
The earthquake ground motion can be divided into two groups: far field motion (FF) and near-field motion (NF) (Faisal, Riza, and Hadibroto, 2018; Kalkan and Kunnath, 2006). The near-field ground motion is defined as the earthquake ground motion that is recorded in a seismic station that is less than 15 kilometers away from the ruptured fault zone. It has distinct signatures in both its velocity and displacement forms, (Figure 1), which is unobservable in the far-field motion. Numerous sources already discussed the major impact of near-field ground motion with pulse (or fling-step) on the multi-story RC frames (e.g., Rashidi et al., 2019; Champion and Liel, 2012; Majid et al., 2010; Zahid, Majid, and Faisal, 2017). However, these studies do not particularly explain the effect of the displacement fling-step pulse on the concrete frames.
Figure
1 a)
far-field earthquake, b) near-field earthquake with velocity pulse effect, and
c) near-field earthquake with the displacement fling-step effect
In addition,
the influence of a repeated near-field earthquake propagates a bigger drift as
compared to the effect of a single earthquake. Again, the effect of multiple
earthquakes incorporating only near-field ground motion is not properly
investigated yet, especially the impact of multiple earthquakes containing the
displacement fling-step pulse on the RC frames. This is, partially, due to the
limited available records. Therefore, the aim of this research is to determine
the likelihood of near-collapse of the RC frames when subjected to a sequence
of near-field earthquakes containing the displacement fling-step effect. The
case study is based on the RC frames that are designed and built in Indonesia.
2.1. RC Frame
Model
The evaluated
archetype moment resisting frames consists of 5-, 10-, 15- and 20-story RC
structures with regular shape of floor plans, masses, and stiffness (Figure 2a
and 2b). This study assumes that the RC special moment resisting frame (MRF)
with R = 8 is constructed on soft soil in Banda Aceh City, Indonesia, whilst
the intermediate and ordinary MRFs with R = 5 and 3, respectively, are
constructed on medium and hard soils in the same city. The structural model's
plan view and the model's frame section are shown in Figure 2. The length of
all beams are equivalent at 6.0 m, and the height of all columns is 3.5 m, with
the exception of the bottom floor, where the column height is 4.5 m. The
concrete and rebar yield strengths used in all models are fc' 40 MPa and fy 400
MPa. The natural period of the structural model is 0.41 s, 0.80 s, 1.16 s, and
1.58 s for 5-, 10-, 15-story, and 20-story RC frames, respectively.
2.2. Elements
Strength
Figure 2 a) The plan view, b) 2D
frame models, and c) Modified-Takeda hysteresis and its backbone curve for
lumped plasticity model of nonlinear inelastic elements.
2.2. Rotation Capacity
2.3.
Strength Degradation
2.4. Ground Motions and Intensity Measure
Generally, there are 2 types of ground
motions employed in earthquake sequence study on the structural response,
namely as-recorded mainshock-aftershock and artificial repeated earthquake.
Since the as-recorded mainshock-aftershock sequences for motions containing
fling-step pulse are scarce, therefore, the ground motion used in this study is
artificially repeated earthquakes. These ground motions are selected from the
available records in Pacific Earthquake
Engineering Research (PEER) Next
Generation Attenuation (NGA) and COSMOS. The selection criteria are based
on magnitude, near-field source-to-site distance (15 km), fault mechanism,
and soil type. Table 1 shows the selected records containing near-field motion
with fling-step effects.
Table 1 List of selected records of near-field ground motion containing
fling-step pulse effect sourced from PEER NGA and COSMOS
|
Record No |
Year |
Earthquake |
MW |
Station |
Dist.(km) |
PGA (g) |
PGV (cm/s) |
PGD (cm) |
|
1 |
1999 |
Chi-Chi |
7.6 |
TCU052 |
1.8 |
0.35 |
178.00 |
493.52 |
|
2 |
1999 |
Chi-Chi |
7.6 |
TCU068 |
3.0 |
0.50 |
277.56 |
715.82 |
|
3 |
1999 |
Chi-Chi |
7.6 |
TCU074 |
13.8 |
0.59 |
68.90 |
193.22 |
|
4 |
1999 |
Chi-Chi |
7.6 |
TCU084 |
11.4 |
0.98 |
140.43 |
204.59 |
|
5 |
1999 |
Chi-Chi |
7.6 |
TCU129 |
2.2 |
0.98 |
66.92 |
126.13 |
|
6 |
1999 |
Kocaeli |
7.4 |
Yarimca |
3.3 |
0.23 |
88.83 |
184.84 |
|
7 |
1999 |
Kocaeli |
7.4 |
Izmit |
4.3 |
0.23 |
48.87 |
95.49 |
|
8 |
1999 |
Chi-Chi |
7.6 |
TCU102 |
1.2 |
0.29 |
84.52 |
153.88 |
|
9 |
1999 |
Chi-Chi |
7.6 |
TCU089 |
8.3 |
0.34 |
44.43 |
193.90 |
|
10 |
1999 |
Chi-Chi |
7.6 |
TCU049 |
3.3 |
0.27 |
54.79 |
121.77 |
|
11 |
1999 |
Chi-Chi |
7.6 |
TCU067 |
1.1 |
0.48 |
94.31 |
181.25 |
|
12 |
1999 |
Chi-Chi |
7.6 |
TCU075 |
3.4 |
0.32 |
111.79 |
164.36 |
|
13 |
1999 |
Chi-Chi |
7.6 |
TCU076 |
3.2 |
0.33 |
65.93 |
101.65 |
|
14 |
1999 |
Chi-Chi |
7.6 |
TCU072 |
7.9 |
0.46 |
83.60 |
209.67 |
|
15 |
1999 |
Chi-Chi |
7.6 |
TCU065 |
2.5 |
0.76 |
128.32 |
228.41 |
|
16 |
1999 |
Chi-Chi |
7.6 |
TCU078 |
8.3 |
0.43 |
41.88 |
121.23 |
|
17 |
1999 |
Chi-Chi |
7.6 |
TCU082 |
4.5 |
0.22 |
50.49 |
142.78 |
|
18 |
1999 |
Chi-Chi |
7.6 |
TCU128 |
9.1 |
0.14 |
59.42 |
91.05 |
|
19 |
1999 |
Chi-Chi |
7.6 |
TCU071 |
4.9 |
0.63 |
79.11 |
244.05 |
|
20 |
1994 |
Northridge-01 |
6.7 |
LA-Sepulveda |
6.7 |
0.46 |
13.80 |
26.13 |
The intensity measure (IM)
employed in this study is RSA(T1). All the selected records
are scaled up and down by referring to the elastic designed spectral
acceleration (Figure 3a) at the natural period of the model considered, RSA(T1),
as demonstrated in Figure 3b. The design spectra for Banda Aceh City is
depicted in Figure 3a, which is developed based on the Indonesian seismic code
(SNI 1726:2012) (BSN, 2012). The Indonesian code is originally adopted
from standard ASCE/SEI 7-10 (ASCE, 2013). In order to model the
artificial repeated earthquakes, all the scaled ground motions are then paired
randomly by adding the 50 seconds of zero motions in between two, and/or three
scaled motions (Figure 3c) to make the free vibration on the structure exhibit
properly before the next earthquake motion started. The study used single, 2-
and 3-times repeated earthquakes to be induced on the RC moment resisting
frames (MRF) model.
2.5. Structural Analysis and Collapse Limit
State
In the design phase, the two dimensional of 3-, 10-, 15 and 20-story RC frames are analyzed with the response spectrum method to get the design flexural force. The elastic design phase complies with the Indonesian Standard SNI 1726:2012 (BSN, 2012), which is nearly identical with the ASCE/SEI 7-10 (ASCE, 2013). The 2D nonlinear inelastic response history analysis with lumped plasticity model is conducted to define the near-collapse state of the system using Ruaumoko 2D v.4.0 (Carr, 2010). This analysis is done in line with the seismic performance assessment guideline as stipulated in FEMA P-695 (FEMA, 2009).
Figure 3 Model of earthquake ground motion: a) Elastic design spectra for
Banda Aceh City, b) Illustration of the ground motion scaling process, (c)
example of 3 times repeated earthquakes
The
incremental dynamic analysis (IDA) (Vamvatsikos
& Cornell, 2002) is utilized to define the interstory drift (IDR)
for the near collapse state, which is the same as the engineering demand
parameter (EDP). In the IDA, the IM = RSA(T1) is repeatedly scaled in
order to find the IM level at which each ground motion causes EDP’s failure
criterion such as near-collapse or collapse. The near-collapse limit state of
IDR = 2.0% is employed based on the requirement stipulated in Indonesian
seismic code, as well as in ASCE 7-10. From IDA, the following parameters namely, , median and standard deviation, respectively, are
defined by fitting the interpolated IM through the method of moments as follow:
2.6. Probability of Near Collapse
The probability of near collapse (or any limit state of interest) is commonly expressed by the fragility function, which is developed through a log normal cumulative distribution function as follows:
where P[D d |R=RSA(T1)] is the probability of reaching or exceeding the
collapse state (the so-called probability near collapse), while the
structure is induced by a ground motion with R=RSA(T1);
is the standard
lognormal cumulative distribution function;
is the median of the ground motion that will cause collapse; and
is the standard deviation of the
ground motion that will cause near-collapse. In developing the fragility
function, the result from the IDA doesn’t always achieve the targeted collapse
limit state. A statistical tool proposed by Baker
(2015) is useful to repair the data in order to estimate the fragility
function. The study also adopts the recommendation of FEMA P-58 guidelines in
order to always increase the logarithmic standard deviation (by adding
= 0.1). It is done so since the uncertainty
in the analytically-based fragility curve could not adequately and accurately
represent the true variability (Porter, Kennedy, and
Bachman, 2007).
This
section is discussed based on the median value of probability near collapse, , to
capture the increment of effect of the repeated earthquake on the system.
Moreover, the standard deviation of the cumulative distribution of IM=RSA(T1),
, is also used to discuss the decrease of IM
required to produce near-collapse state. This value will affect the slope of
the diagonal line of fragility curve. The result of
and
that are used to construct the fragility curve is
provided in Table 2. The
table indicates that
is found within the range of 0.16 to 0.33
for all MRFs considered in the study. Porter, Kennedy, and
Bachman (2007) find that commonly
is
within the range of 0.2 to 0.6, after adding the uncertainty factor
whereas Baker (2015) explains that
= 0.4 is
commonly used to develop the fragility function, without the uncertainty
factor. Basone et
al. (2017) assess the seismic fragility curve of RC buildings with
T1 =0.34 s and find the standard deviation for the dataset, which ranged from
0.29 to 0.60. They evaluate the RC building up to the collapse state. Porter et
al. also explains that the quality of the dataset is high if the
or
differences
are found to be ³ 20%. The
and
listed
in Table 2 clearly demonstrates the
value difference, as indicated by Porter et al. Therefore, it can be said that
the
and
resulted
from this study is well defined, thus it is capable to produce high quality
fragility functions.
Figures 4 - 6 have depicted the fragility
curve of the 5-, 10-, 15-, and 20-story of special (R=8), intermediate (R=5),
and ordinary (R=3) MRFs under the effect of single earthquake (1XE), 2-times
earthquake (2XE) and 3-times earthquakes (3XE). Overall, the figures clearly
demonstrate that as the number of stories and R increased, the IM required to
produce near-collapse state decreased. This rule of thumb confirms that the
process conducted in this study is in the right path. Figure 4a indicates that IM = RSA(T1) = 2.63
g is required to achieve the probability of near-collapse for 5-story ordinary
MRF. This IM is slightly decreased to
2.38 g and 2.30 g for 2XE and 3XE, respectively, to achieve near-collapse
probability. A similar condition is also indicated in 10- and 20-story ordinary
MRFs in achieving the probability near-collapse (Figures 4b and 4c). For this
ordinary MRF, the maximum effect of 2XE and 3XE is found to be exhibited on the
15-story and 20-story MRFs, respectively. In average, the 2XE has influenced
the response of 15-story MRF to be 14.48% more likely than 1XE in achieving the
near-collapse state, whereas 3XE has affected 20-story MRF of 24.4% more likely
than 1XE (Figures 4c and 4d).
Figure
6 Probability
of near collapse for 5-, 10-, 15-, and 20-story RC frames for R = 8 induced by
repeated earthquake with fling-step effects
The near-collapse
probability for intermediate and special MRFs is depicted in Figures 5 and 6,
respectively. The figures indicate that the effect of R pushes the diagonal
line of the fragility curve to the left to become a vertical-like line. These
conditions mean that lower IM is more likely achieve the near-collapse
EDP. In the case of intermediate MRF,
the study finds that 2XE produces the maximum effect on the 20-story MRF
(Figure 5d). The 2XE makes the decrement of IM reached 27.0% in achieving near-collapse
EDP, whereas 3XE has maximum affection on the 15-story MRF, which is about
11.13 % more likely than the IM of 1XE (Figure 5c). Similar trend is indicated
for special MRFs affected by single and repeated earthquakes in Figure 6. The
IM of probability near collapse is clearly decreased as the number of the story
increased.
In Table
2, the median for special and intermediate MRFs, which have fundamental periods
of T1 = 0.41 s to 1.58 s,
are found within the range of = 0.36 to 2.10. This result is much lower than the
median IDA result of m = 0.98 to 5.36 for the collapse capacity of modern
ductile concrete MRF with T1
= 0.42 s to 1.69 s done by Champion and Liel (2012).
It is obviously lower since this study is based on the near-collapse state,
which is not the collapse state as reported in Champion and Liel’s study. In
fact, this study also found the collapse state median IDA of
= 0.71
to 4.67, which would be discussed in the upcoming paper.
Kalantari and
Roohbakhsh (2019)
found the fragility curve of the 4-story RC structure is based on the
dispersion of b= 0.82 to
1.04. Their study also explains that the fragility curve of a 15-story RC
structure is developed based on b =
0.96 to 1.07. Aljawhari et al. (2021)
reports that the dispersion of b =
0.359 is used to generate the fragility curve of a 4-story RC building. In this
study, we obtained b =
0.27 for 5-story, and b =
0.29 for 15-story RC special MRF. The significant gap shown in result b is mainly caused by the handling of the
uncertainty issues (quality of the dataset) for each study. Therefore, the
comparison of those results shall not be made straightforward. However,
statistically, we may refer to Porter, Kennedy, and
Bachman (2007) and Baker (2015) for the
common thresholds of dispersion in developing fragility curves, i.e. b = 0.2 to 0.4. It means that the fragility
curves of this study and the one in the study of Aljawahari et al. are
the common curves to be used as the probability of the limit state function of
RC structures.
Shokrabadi, Burton, and Stewart (2018) already
explains that the response RC frames with T1
= 1.12 s and 1.71 s are increased significantly
to 30% - 50% when aftershock combines with mainshock motions. This increases
the collapse probability to be 1.5
and 3.5 times more likely. The
evaluation of a 4-story regular RC frame made by Oggu
and Gopikhrisna (2020) finds that the probability of the considered IM
decreases to 23.91%, which is smaller than the effect of a single earthquake. Di Sarno and Pugliese (2021) reported that the
effect of repeated earthquakes on existing 4-story RC structures caused the
probability of considered IM to decrease to 17% in comparison with the effect
of a single earthquake. In this study, the probability of IM for 5-story RC
special MRF under repeated earthquakes is decreased to 25.94%, which is smaller
than the effect of a single earthquake. These significant gaps in the
probability of IMs are mainly caused by the different methods of modeling the
repeated earthquake and the selection of ground motion.
The probabilistic seismic assessment of
reinforced concrete (RC) moment resisting frame (MRF) in Indonesia has been
presented. The
assessment makes use of the single, twice, and three times repeated earthquakes
(referred to as 1XE, 2XE, and 3XE) that contain the displacement fling-step
pulse. Four archetype RC frames were considered, namely 5-, 10-, 15-, and 20-story with
response modification factor R = 8, 5, and 3, which represents special,
intermediate, and ordinary MRF. Therefore, this study concluded that repeated
earthquakes is more likely producing near-collapse IM 27.0% earlier than the IM
of single earthquake, particularly on the intermediate MRF. In this case, the
near-collapse probability of ordinary MRF is posed slightly differently with
intermediate MRF. For special MRF, it is found that the near-collapse
probability may increase significantly due to the effect of 2XE and 3XE. It is
indicated by the 22.19% decrement of IM in producing near-collapse EDP, which
was lower than IM for 1XE. In average, the
2XE which might be producing the near-collapse IM of 16.58% is more likely to
occur on the all considered RC frames in comparison with 1XE. This probability
was larger than 3XE effect, which 9.45% more likely to exhibit on the frames
compared with the effect of 1XE. In average, the repeated earthquakes
containing fling-step pulse may increase the near-collapse probability of
special, intermediate, and ordinary RC frames to reach 13.81%, 12.67%, and
12.56%, respectively. In comparison to 1XE, the trends of the effect of 3XE on
this near-collapse probability do not always produce a superior effect when
compared to the effect of 2XE. Indeed, besides the repeated earthquakes
containing filing-step pulse, the variations in considered story heights, R,
and rotation capacity also contributes to the critical effect on the seismic
performance of the structure.
We gratefully thank the Fundamental Research grant with contract number
05/II.3-AU/UMSU-LP2M/C/2021 in the year 2021 for sponsoring this study, which
were awarded to the first author. The authors wish to thank the undergraduate students who were involved in this research as
numerators.
Amadio, C.,
Fragiacomo, M., Rajgelj, S., 2003. The effects of repeated earthquake ground motions on the nonlinear
response of SDOF systems. Earthquake
Engineering & Structural Dynamics, Volume 32(2), pp. 291–308
Aljawhari, K.,
Gentile, R., Freddi, F., Galasso, C. 2021. Effects of ground-motion sequences
on fragility and vulnerability of case-study reinforced concrete frames. Bulletin
of Earthquake Engineering, Volume 19(15), pp.
6329–6359
Amiri, G.G., Rajabi, E., 2018.
Effects of consecutive earthquakes on increased damage and response of
reinforced concrete structures. Computers & Concrete, Volume
21(1), pp. 55–66
ASCE, 2013. Minimum Design Loads for Buildings and Other
Structures, ASCE Standard ASCE/SEI 7-10,
American
Society of Civil Engineers, Reston
Baker, J.W.,
2015. Efficient analytical fragility function fitting using dynamic structural
analysis. Earthquake Spectra, Volume 31(1), pp. 579–599
Basone, F.,
Cavaleri, L., Di Trapani, F., Muscolino, G., 2017. Incremental dynamic based
fragility assessment of reinforced concrete structures: stationary vs.
non-stationary artificial ground motions. Soil Dynamics &
Earthquake Engineering, Volume 103,
pp. 105–117
Carr, A.J., 2010. Ruaumoko Manual Volume: 1, Theory and User
Guide to Associated Program. University of Canterbury
Champion,
C., Liel, A., 2012. the effect of near-fault directivity on building seismic
collapse risk. Earthquake Engineering & Structural Dynamics, Volume
41(10), pp. 1391–1409
Di Sarno, L.,
Pugliese, F. 2021. Effects of mainshock-aftershock sequences on fragility
analysis of RC buildings with
ageing. Engineering Structures, Volume
232, p. 111837
Di Trapani, F., Malavisi, M., 2019.
Seismic fragility assessment of infilled frames subject to mainshock/aftershock
sequences using a double incremental dynamic analysis approach. Bulletin
of Earthquake Engineering, Volume 17(1), pp. 211–235
Dymiotis,
C., Kappos, A.J., Chryssanthopoulos, M.K., 1999. Seismic reliability of RC frames with
uncertain drift and member capacity. Journal
of Structural Engineering, Volume 125(9), pp. 1038–1047
Faisal, A.,
Majid, T. A., Hatzigeorgiou, G. D. 2013. Investigation of Story Ductility
Demands of Inelastic Concrete Frames Subjected to Repeated Earthquakes. Soil
Dynamics & Earthquake Engineering, Volume 44, pp. 42–53
Faisal, A.,
Riza, F.V., Hadibroto, B. 2018. Global ductility demands of RC frames with
various post-yield stiffness ratio and ductility capacity ratio under
near-field earthquakes
Fardis,
M.N., 2007. Guidelines for displacement-based
design of buildings and bridge. Pavia, Italy: IUSS Press
FEMA, 2009. Quantification of Building Seismic
Performance Factors. Rep. FEMA P-695, Federal Emergency Management Agency, Washington,
D.C
Hatzigeorgiou,
G.D., Liolios, A.A., 2010. Nonlinear behaviour of RC frames under repeated strong ground motions. Soil
dynamics & Earthquake Engineering, Volume 30(10), pp. 1010–1025
Hatzivassiliou,
M., Hatzigeorgiou, G.D., 2015. Seismic sequence effects on three-dimensional
reinforced concrete buildings. Soil Dynamics & Earthquake Engineering,
Volume 72, pp. 77–88
Haselton,
C.B., Liel, A.B., Deierlein, G.G., Dean, B.S., Chou, J.H., 2010. Seismic collapse
safety of reinforced concrete buildings. I: Assessment of ductile moment frames.
Journal of Structural Engineering, Volume 137(4), pp. 481–491
Kalkan, E.,
Kunnath, S.K., 2006. Effects of fling step and forward directivity on seismic
response of buildings. Earthquake Spectra, Volume 22(2), pp. 367–390
Kalantari, A.,
Roohbakhsh, H. 2020. Expected seismic fragility of code-conforming RC moment
resisting frames under twin seismic events. Journal of Building Engineering, Volume
28, p. 101098
Kappos, A.,
Manafpour, A., 2001. Seismic design of R/C buildings with the aid of advanced analytical
techniques. Engineering
Structures, Volume 23, pp. 319–332
Majid, T.A.,
Wan, H.W., Zaini, SS., Faisal, A., Wong, Z.M., 2010. The effect of ground
motion on non-linear performance of asymmetrical reinforced concrete frames. Disaster
Advances, Volume 3(4),
pp. 35–39
Mase, L.Z., 2018, Reliability study of
spectral acceleration designs against earthquakes in Bengkulu
City, Indonesia, 2018. International
Journal of Technology, Volume
9(5), pp. 910–924
National Standardization Agency of Indonesia (BSN), 2012. Design Code of Earthquake Resistance
Structures for Building and Non-Building, SNI
1726:2012. Jakarta
Oggu, P.,
Gopikrishna, K. 2020. Assessment of three-dimensional RC moment-resisting
frames under repeated earthquakes. Structures, Volume 26, pp. 6–23
Porter, K., Kennedy, R., Bachman, R., 2007.
Creating fragility functions for performance based earthquake engineering. Earthquake Spectra, Volume 23, pp. 471–89
Prakoso, W.A., Rahayu, A., Sadisun, I.A.,
Muntohar, A.S., Muzli, M., Rudyanto, A., 2017. Comparing shear-wave
velocity determined by MASW with borehole measurement at Merapi Sediment in Yogyakarta. International
Journal of Technology, Volume 8(6),
pp. 993–1000
Pramono, S.,
Prakoso, W.A., Rohadi, S., Karnawati, D., Permana, D., Prayitno, B.S.,
Rudyanto, A., Sadly, M., Sakti, A.P., Octantyo, A.P., 2020. Investigation of
Ground Motion and Local Site Characteristics of the 2018 Lombok Earthquake
Sequence. International Journal of Technology, Volume 11(4),
pp. 743–753
Rashidi, A.,
Majid, T.A., Fadzli, M.N., Faisal, A., Noor, S.M., 2017. A Comprehensive Study
on the Influence of Strength and Stiffness Eccentricities to the on-Plan
Rotation of Asymmetric Structure. In: Proceedings of the International
Conference of Global Network for Innovative Technology and Awam International
Conference in Civil Engineering (IGNITE-AICCE’17): Sustainable Technology and
Practice for Infrastructure and Community Resilience
Shokrabadi,
M., Burton, H.V., Stewart, J. P. 2018. Impact of sequential ground motion pairing on Mainshock-Aftershock structural
response and collapse performance assessment. Journal of Structural
Engineering, Volume 144(10),
p. 04018177
Tahara, R.M.K., Majid, T.A., Zaini, S.S., Faisal, A., 2017. Effect of repeated
earthquake on inelastic moment resisting concrete frame. In: Proceedings of the
International Conference of Global Network for Innovative Technology and AWAM
International Conference in Civil Engineering, Penang, 8-9 August, Malaysia
Vamvatsikos, D., Cornell, C.A.,
2002. Incremental dynamic analysis. Earthquake Engineering &
Structural Dynamics, Volume 31(3),
pp. 491–514
Zahid, M. Z. A. M., Majid, T. A., Faisal, A., 2017. The effect of
behaviour factor on the seismic performance of low-rise and high-rise RC buildings.
Journal of Engineering Science and
Technology, Volume 12(1), pp. 031-041
Zareian, F., Krawinkler, H. 2010. Structural system parameter selection based on collapse potential of buildings in earthquakes. Journal of Structural Engineering, Volume 136(8), pp. 933–943
