Nonlinearities Influence to RF Satellite Downlink Model with QAM and Raised Square Cosine Filter
Published at : 25 Jan 2024
Volume : IJtech
Vol 15, No 1 (2024)
DOI : https://doi.org/10.14716/ijtech.v15i1.3887
Vujovic, I., Susko, L., Kuzmanic, I., Petkovic, M., 2024. Nonlinearities Influence to RF Satellite Downlink Model with QAM and Raised Square Cosine Filter. International Journal of Technology. Volume 15(1), pp. 230-239
| Igor Vujovic | University of Split, Faculty of Maritime Studies, Signal Processing, Analysis and Advanced Diagnostics Research and Education Laboratory (SPAADREL), Rudera Boskovica 37, 21000 Split, Croatia |
| Ljubo Susko | Croatian Military, Communications and Electronic Warfare, Zrinjsko-Frankopanska 183, 21000 Split, Croatia |
| Ivica Kuzmanic | University of Split, Faculty of Maritime Studies, Signal Processing, Analysis and Advanced Diagnostics Research and Education Laboratory (SPAADREL), Rudera Boskovica 37, 21000 Split, Croatia |
| Miro Petkovic | University of Split, Faculty of Maritime Studies, Signal Processing, Analysis and Advanced Diagnostics Research and Education Laboratory (SPAADREL), Rudera Boskovica 37, 21000 Split, Croatia |
Reliability of
communications is of vital importance in military applications. Constellations
are connecting coded words at different ends of the communication channel that
indicate the correctness of the transmitted message. In this paper, we compare
the influence of the selected nonlinearity in the transmit amplifier on the
constellation diagrams in radio frequency (RF) geostationary satellite downlink
and bit-error-rate (BER). Two cases were analyzed: negligible and severe noise
in the communication channel. Considering the cubic, hyperbolic tangent, Saleh,
Ghorbani, and Raap models, it is shown that the Raap and Saleh models can be
used for the lowest BERs when the noise is negligible. In case of severe noise,
it is best to use the Raap model from the set of nonlinearities considered. The
ANOVA-test showed that there is a dependence between the Raap and Saleh models
in the presence of negligible noise, but not in the presence of severe noise.
BER; Constellation diagrams; High power amplifier; Satellite downlink model
The importance of satellite communications
for maritime and navy applications is well-known and increasing. If a
transmitted message is altered beyond reliable identification, there could be
significant consequences for warfare. Hence, communications reliability studies
are more important than ever. Although some problems in wireless communications
were considered in (Kurniawati et al., 2023;
Pamukti, Wijayanto, and Liaw, 2023), and path losses in (Lukman et al.,
2022), problems considered in this paper were not investigated in these
references. The satellite component plays a fundamental role in Universal
Mobile Telecommunication Systems (UMTS) (Janaaththanan,
2008).
High power
amplifiers (HPAs), which are highly sensitive to nonlinearities, were the focus
of Lakhwal, Pal, and Kumar (2012). Because of these nonlinear
responses, signal distortions were also amplified. The paper presents an
adaptive method for linearizing the HPA response using a polynomial. There
isn’t comparative analysis of the nonlinearities’ effects studied yet.
A framework for RF systems modeling is described in (Arabi and Ali, 2008). Simulink was used and Quadrature Amplitude Modulation (QAM) was considered. However, only one nonlinearity was considered. On the contrary, the subject of this paper is a comparison of various nonlinearities. Bawa, Pal, and Gupta (2013) concluded that polynomials up to the 5th order is useful since higher orders have negligible effects. It can be seen that the most popular nonlinearity is the polynomial. Current trends include multicarrier waveforms and non-symmetrical spectral shaping of subchannels (Jošilo et al., 2014), exploration of RF distortions massive MIMO (Multi-Input, Multi-Output) Systems in millimeter-wave (Khansefid et al., 2016), digital precompensation for multicarrier satellite communications (Kelly et al., 2015), Ku/Ka band satellite services (SES, 2017), and MIMO satellite communications (Ramamurthy, 2018) or novel materials for antenna designs. Wang et al., (2022), (Gupta et al., 2019) focus more on hardware for HPA. Some aspects of nonlinearities in HPAs are also considered in the works of Ssimbwa et al. (2022) and Mukherjee, Lajnef, and Krikidis (2020). The importance of this research is emphasized by references on their compensation, e.g. (Maltsev et al., 2022). All of the above topics could be addressed separately.
The contributions of the paper are:
- pointing out an
example linking marine electrical engineering education with the practice of
readers working in parallel with their studies,
- linking work
processes with theory in order to the improve theoretical knowledge of the
operator, and help readers to combine study and work,
- simulation in
Matlab/Simulink, linked to a problem from practice to complete the education
and finish the appropriate level of training,
- comparative analysis
of the influence of the different models (cubic, hyperbolic tangent, Saleh,
Ghorbani, Raap) on the constellations.
In this paper, QAM is considered for satellite communications. The paper is organized as follows. In section two, the considered model of satellite downlink is presented. In section three, nonlinearities in HPA are defined. The simulation results are presented in the fourth section. The last section contains the conclusions.
Considered System and Components
The considered system consists of three parts: the satellite’s downlink transmitter, the downlink path (corresponding to the influence of conditions in the transmitting medium, i.e. atmospheric conditions), and the ground station downlink receiver. Ideally, the receiver should read the signal without error. Constellation diagrams show the dispersion of the received signals. The downlink transmitter consists of: QAM modulator, transmit filter (in this case raised cosine transmit filter), HPA, and antenna gain. HPA introduces nonlinearity in real cases. One method to linearize the power amplifier (PA) is to introduce predistortion into the modeling (Raich, 2004). Ideal PA can be with and without memory effects, but wideband signals also tend to introduce memory effects. Memory effects can also be caused by electrical or/and electrothermal sources. Hence, HPAs are modeled with nonlinear functions to compensate for memory effects, and nonlinearity is used instead of memory effects (Šuško, 2013). In memoryless systems, the output is a function of the input at the current time, there are no energy-storing components, and the output is in phase with the input. Input-output (I/O) relationship should be frequency-independent. HPA is also modeled to compensate for system degradation due to amplifier nonlinearities, intermodulation effects, etc. Memoryless models are i.e. polynomial, Saleh, Ghorbani, or Rapp. The transfer function (TF) of the raised cosine filter can be expressed as square cosine. The inputs are the roll-off factor (a) and the cut-off frequency (1/Ts), as in equation (1):
Impulse response is given with equation (2):
The polynomial models used in the Results section are cubic and hyperbolic tangent. In general, a finite order polynomial model fitted to the I/O measurements of an amplifier is defined as follows in equation (3):
where N is the order of the polynomial and L is the number of measured data. The cubic polynomial has components up to the 3rd order. The hyperbolic tangent has 1st, 3rd, and 5th order variables (Bawa, Pal, and Gupta, 2013). The Saleh model (O'Droma et al., 2009) is considered as a standard. It equation (4) defines the AM/AM and AM/PM TFs as:
where r(t) is the modulated envelope and Pmax is the maximum
saturation point of the amplifier. In the Ghorbani model (Sajedin and Ghorbani, 2014), the TFs are defined
as equation (5):
where are AM/AM parameters used to calculate amplitude gain for input signal A, and
AM/PM parameters for phase change computation. In the Raap model (KrishneGowda et al., 2016), the smoothness factor, p, and the output saturation level, A0, are used to calculate the amplitude gain for the input signal equation (6):
The simulation is performed for the following parameters: satellite
altitude 35600 km, frequency 4 GHz, transmit antenna diameter 0.4 m, receive
antenna diameter 0.4 m, phase noise 100 dBc / Hz. HPA nonlinearity is set to
values of 30 dB for negligible, and 1 dB for severe. Phase
noise is set to negligible (-100 dBc/Hz@100 Hz) and to severe (-48 dBc/Hz@100
Hz). Severe noise is high enough to cause errors even without thermal noise or
other RF impairments. Figure 1 shows constellations for various analyzed nonlinearities.
As can be seen, the figures on the right side of Figure 1 have higher
amplitudes. Figure 1(a) shows 4.4 times magnification. Figure 1(b) shows around
7.7 times magnification. Figure 1(c) shows magnification of around 5, Figure
1(d) 4.8, and Figure 1(e) around 5. The figures on the right side look more
clustered, but it could be a visual effect due to magnification. As can be seen
in Figure 1, the real constellation looks different from the ideal case, which
is expected. However, a different model results in a different deviation from
the center of the cluster, i.e. the ideal arrangement of the constellation. The
important question to be further explored is how large interference can be that
leads to false detection of the transmitted signal.
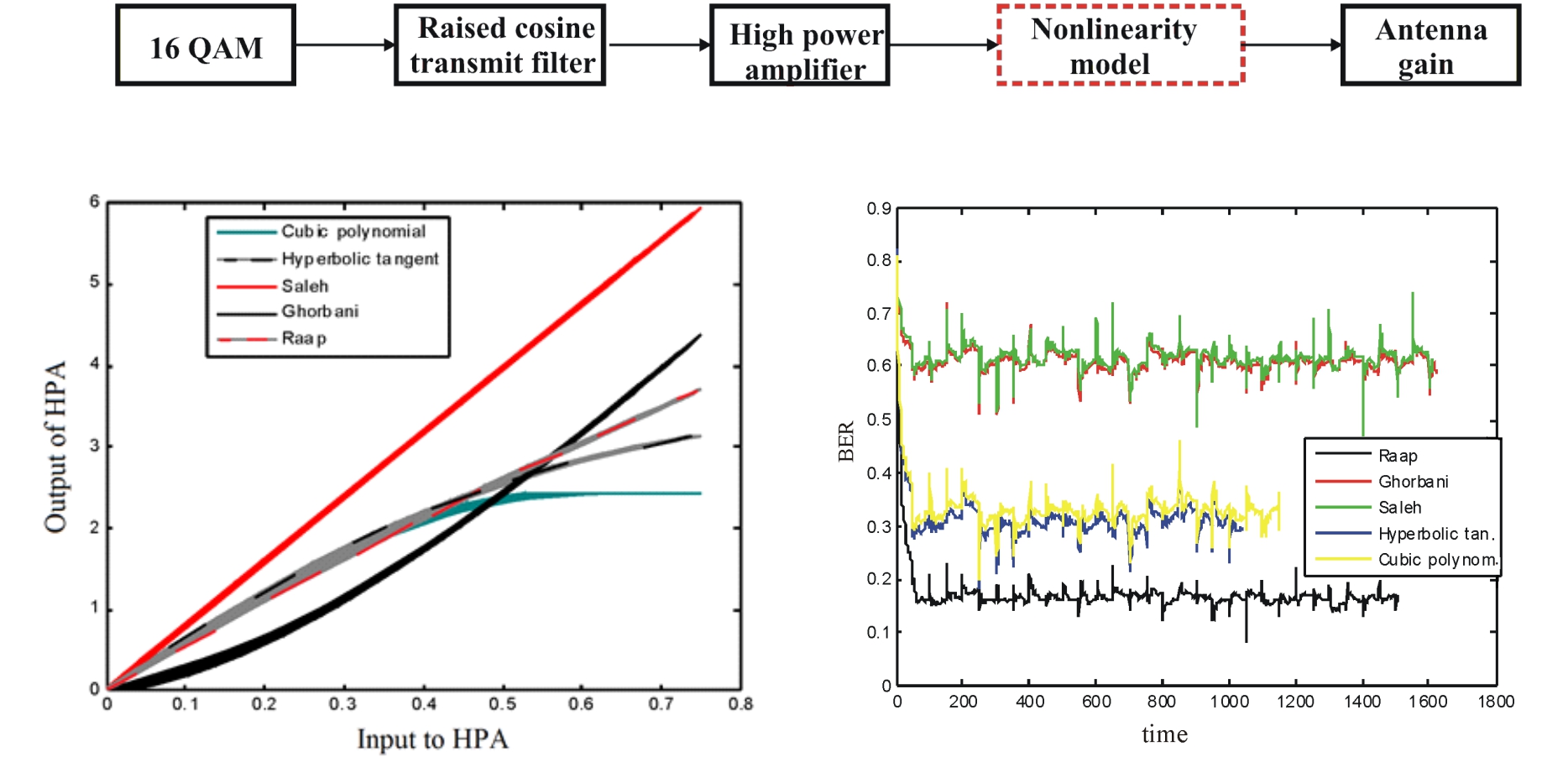
Figure 2(a) shows the input/output characteristics of HPA for various nonlinearities. It can be seen that the HPA characteristic is linear for Saleh, slow exponential growth is exhibited by Gharboani, and other models result in saturation (asymptotic behavior).
Figure 1
(continued) Nonlinearities in HPA: (d) hyperbolic tangent - constellation
before (left) and after (right) HPA; and (e) Raap – constellation before (left) and after (right) HPA
Figure 2 I/O characteristic of HPA for a)
the first scenario, b) the second simulation scenario
An
example of BER for different models is shown in Figure 3 (a). Figure 3 (b)
shows the difference between hyperbolic and Ghorbani, cubic and Ghorbani, and
Raap and Ghorbani models. Noise is added to the simulation to show the changes
in the presence of strong noise in the communication channel. For the following
results, the simulation was performed with the following parameters: satellite
altitude of 35600 km, frequency of 4 GHz, transmit antenna diameter of 0.4 m,
receive antenna diameter of 0.4 m, noise temperature of 290 K, HPA backoff
level 1 of dB, and phase noise of - 48 dBc / Hz. While the Saleh model can lead
to a linear O/I characteristic, other models are nonlinear. Figure 3(b)
indicates that the Raap and Ghorbani models have differences in BER only when
they are not in a steady state, e.g. at the beginning in the time domain.
Moreover, it can be seen that the calculation of BER leads to high values at
the beginning and to non-deterministic values for the rest of the time.
Figure 3 (a)
BER for different models; and (b) difference of BERs for different models
Figure 4(a) shows the BERs in the case of severe noise in the
communication channel for all five models considered. It can be seen that the
Raap model has the lowest BER, while Saleh and Ghorbani have the highest BERs.
Figure 4(b) confirms the conclusions of model quality based on BER and shows
BER differences for the low and high noise scenarios in the communication
channel.
Figure 4 (a) BER for the case of
severe noise in the communication channel; and (b) BER difference for the same
models with negligible and severe noise in the communication channel
Figure 5 shows the simulation results for the
input/output difference for the low noise case. Figure 5(a) shows the absolute
value of the difference for all considered nonlinearities in the enlarged part.
Figure 5(b) shows the phase diagram of the difference, enlarged part. It can be
seen that the Ghorbani and Saleh curves have the same values at the last time
point. The Saleh and Raap curves overlapped in earlier time periods. The
hyperbolic tangent nonlinearity-produced curve overlaps with the cubic curve.
It can be seen that differences are greater in the case of negligible than in
the case of severe noise.
|
Figure 5 I/O difference for
negligible noise (a) absolute value; (b) phase |
Figure 6 shows the difference between the
input and output signals in the case of severe noise. Figure 6(a) shows the
absolute value of the difference signal. Figure 6(b) shows the phase of the
difference (I/O) signal for all 10,000 points.
Figure 6
Input/output difference signal for the case of severe noise: a) absolute value,
b) phase
Figure
7 shows the difference between cases with negligible noise and those with
severe noise for the same type of nonlinearity. For example, the blue line in Figure
7(a) shows the difference between the phases of the considered cases for cubic
polynomial nonlinearity. Figure 7(b) shows the absolute value of the difference
between cases.
To
check for possible dependencies between the results of the models used, we
performed an ANOVA analysis. This analysis provides the P-value, the
probability that the F-ratio is as large or larger than the observed one. In
addition, the mean square (MS), degrees of freedom (df), and sum of squares
(SS). The critical value of F (Fcrit) is the value that represents
the boundary between dependence and non-dependence between the data groups. The variation between groups accounts for the
overall variation among each group's mean and the overall mean, while the
variation within groups encompasses the total variation in individual values
within each group and their respective group means.
Figure 7 Difference of I/O for two considered cases:
(a) phase; (b) absolute value
As shown in Table 1, based on F>Fcrtit,
it can be concluded that there are no dependencies between all five models in
the presence of negligible noise. In Table 2, it is evident that dependencies
exist between the Saleh and Raap models under the condition of negligible
noise.
Table 1 Results of ANOVA analysis for negligible noise for all considered models
|
Source of Variation |
SS |
Df |
MS |
F |
P-value |
Fcrit |
|
Between Groups |
8.526003 |
4 |
2.131501 |
419.6638 |
0 |
2.373333 |
|
Within Groups |
32.20129 |
6340 |
0.005079 | |||
|
Total |
40.72729 |
6344 |
|
|
|
|
Table 2 Results of ANOVA analysis for negligible noise for Saleh and Raap
|
Source of Variation |
SS |
df |
MS |
F |
P-value |
Fcrit |
|
Between Groups |
3.74E-05 |
1 |
3.74E-05 |
0.006367 |
0.936406 |
3.845128 |
|
Within Groups |
14.90038 |
2536 |
0.005876 | |||
|
Total |
14.90042 |
2537 |
|
|
|
|
Results
in Table 3 show that F>Fcrtit. Table 4 leads to the same
conclusion that the data sets are not dependent on each other.
Table 3 Results of ANOVA analysis for severe noise for all considered models
|
Source of Variation |
SS |
Df |
MS |
F |
P-value |
Fcrit |
|
Between Groups |
161,1764 |
4 |
40.29409 |
21130.53 |
0 |
2.373641 |
|
Within Groups |
9.915948 |
5200 |
0.001907 | |||
|
Total |
171.0923 |
5204 |
|
|
|
|
Table 4 Results of ANOVA analysis for severe noise for Saleh and Raap
|
Source of Variation |
SS |
Df |
MS |
F |
P-value |
Fcrit |
|
Between Groups |
149.5105 |
1 |
149.5105 |
94969.92 |
0 |
3.844556 |
|
Within Groups |
4.729176 |
3004 |
0.001574 | |||
|
Total |
154.2397 |
3005 |
|
|
|
|
Table 5 Results of ANOVA analysis for severe and negligible noise for the Raap
model
|
Source of Variation |
SS |
df |
MS |
F |
P-value |
|
Fcrit |
|
Between Groups |
16.48115 |
1 |
16.48115 |
3699.667 |
0 |
|
3.845128 |
|
Within Groups |
11.29729 |
2536 |
0.004455 |
| |||
|
Total |
27.77844 |
2537 |
|
|
|
|
|
Since
F>Fcrtit, we can conclude that there is no correlation between
severe and negligible noise in the case of the Raap model.
As shown in
Table 1, based on F>Fcrtit, it can be concluded that there are no
dependencies between all five models in the presence of negligible noise. Table
2 shows that there are dependencies between Saleh and Raap when the noise is
negligible. Table 3 shows that in the presence of severe noise, there are no
dependencies for all models considered. Table 4 shows that there are no
dependencies for Saleh and Raap in case of severe noise. Finally, Table 5 shows
somewhat surprising results, as one would expect there to be relationships
between different noise levels within the same nonlinearity model.
Change of a
bit due to scattering in the received constellation could change e.g.
coordinates of the target, which could be vital information. Figure 1 suggests
that encoded words can be significantly altered. Therefore, the transmitted
message can be misinterpreted. In our case, the participant (see the 3rd
contribution in the Introduction) was employed in the military field. Hence, in
his profession, the consequences could lead to influencing decisions in combat
and consequently, since it is military communication, cost soldiers their
lives. To further explore the issue and examine possible dependencies between
the results of the models used, we performed an ANOVA analysis. Implications of
existing dependencies could be that researchers will find a relation between
them.
This
work is based on a student’s master thesis and grant no. KK.01.1.1.02.0018
(EU).
Arabi,
E., Ali, S., 2008. Behavioral Modeling of RF Front End Devices in Simulink. Master’s
Thesis, Chalmers University of Technology, Sweden
Bawa,
S., Pal, M., Gupta, J., 2013. Pre-Distortion Based Linearisation Technique for
Power Amplifiers of Wideband Communication Systems. International Journal of
Scientific & Engineering Research, Volume 4, pp. 726–733
Sajedin,
M., Ghorbani, A., 2014. Nonlinearity compensation for high power amplifiers
based on look-up table method for OFDM transmitters. International Journal of Advanced Computer Science and Information
Technology, Volume 3(4), pp. 354–367
Gupta,
N., Saxena, J., Singh-Bhatia, K., Dadwal, N., 2019. Design of
Metamaterial-Loaded Rectangular Patch Antenna for Satellite Communication
Applications. Iranian Journal of Science and Technology–Transactions on
Electrical Engineering, Volume 43, pp. 39–49
Janaaththanan,
S., 2008. OFDM Based Air Interfaces for Future Mobile Satellite Systems.
Dissertation, University of Surrey, Faculty of Engineering and Physical
Sciences
Jošilo,
S., Pejovi?, M., ?or?evi?, B., Narandži?, M., Nedi?, S., 2014. Multicarrier
Waveforms With I/Q Staggering: Uniform and Nonuniform FBMC Formats. EURASIP
Journal on Advances in Signal Processing, Volume 2014, p. 167
Kelly,
N., Allegue-Martínez, M., Arapoglou, P.D., Zhu, A., 2015. Bandwidth-Constrained
Digital Pre-compensation Technique for Multi-carrier Satellite Communications. International
Journal of Satellite Communications and Networking, Volume 34, pp. 171–194
Khansefid,
A., Minn, H., Zhan, Q., Al-Dhahir, N., Huang, H., Du, X., 2016. Waveform
Parameter Design and Comparisons for Millimeter-Wave Massive MIMO Systems with
RF Distortions. In: 2016 IEEE Globecom Workshop, Washington, pp. 1–6
Kurniawati,
A.M., Sutisna, N., Zakaria, H., Nagao, Y., Mengko, T.L., Ochi, H., 2023. High
Throughput and Low Latency Wireless Communication System using
Bandwidth-Efficient Transmission for Medical Internet of Thing. International
Journal of Technology, Volume 14(4), pp. 932–947
Lakhwal,
P.S., Pal, M., Kumar, V., 2012. Adaptive Lineariser for RF Wideband Power
Amplifier. International Journal of Advances in Computing and Information
Technology, Volume 1(4), pp. 369–377
Lukman, S., Nazaruddin, Y.Y., Ai, B., Joelianto, E.,
2022. Path Loss Modelling for
High-Speed Rail in 5G Communication System. International Journal of
Technology, Volume 13(4), pp. 848–859
Maltsev,
A., Shikov, A., Pudeev, A., Kim, S., Yang, S., 2022. A Method for Power
Amplifier Distortions Compensation at The RX Side for the 5G NR Communication
Systems. In: Proceedings of CECNet, Volume 363, pp. 119–129
Mukherjee, P., Lajnef, S., Krikidis, I., 2020. MIMO
SWIPT Systems with Power
Amplifier Nonlinearities and Memory Effects. IEEE Wireless Communications
Letters, Volume 9, pp. 2187–2191
Pamukti,
B., Wijayanto, A., Liaw, S.-K, 2023. High-Bit-Rate Transmission in Visible
Light Communication System Based on Adaptive Successive Interference
Cancellation Technique. International Journal of Technology, Volume
14(5), pp. 1009–1018
Raich,
R., 2004. Nonlinear System Identification and Analysis with Applications To
Power Amplifier Modeling and Power Amplifier Predistortion. Dissertation,
Georgia Institute of Technology, School of Electrical and Computer Engineering
Ramamurthy,
B., 2018. MIMO for Satellite Communication Systems. PhD Thesis,
University of South Australia
KrishneGowda,
K., Javed, A.R., Wolf, A.C., Kraemer, R., 2016. Parallel Sequence Spread
Spectrum System Simulation with Rapp Model.
Computer Science & Information Technology, Volume 6, pp. 01-07
O'Droma,
M., Meza, S., Lei, Y., 2009. New Modified Saleh Models for Memoryless Nonlinear
Power Amplifier Behavioural Modelling. IEEE Communication Letters, Volume
13(6), pp. 399–401
Satellite
Earth Stations and Systems (SES), 2017. SC-FDMA Based Radio Waveform Technology
for Ku/Ka Band Satellite Service. Technical Report, ETSI TR 103 297 V1.1.1
Ssimbwa, J., Lim, B., Lee, J.-H., Ko, Y.-C., 2022. A Survey on Robust Modulation Requirements for
The Next Generation Personal Satellite Communications. Frontiers in
Communications and Networks, Volume 3, p. 850781
Šuško,
Lj., 2013. QAM
Modulacija I Podignuti Kosinusni Filtar Na Modelu RF Satelitskog Linka (QAM
Modulation and Cos Filter in RF Satellite Down Link Model). Master Thesis, University of Split, Faculty of
Maritime Studies
Wang,
Z., Hu, S., Gu, L., Lin, L., 2022. Review of Ka-Band Power Amplifier. Electronics,
Volume 11, p. 942
